2024年初中科学重点题型复习--浮力计算题(含解析)
文档属性
| 名称 | 2024年初中科学重点题型复习--浮力计算题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 577.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 科学 | ||
| 更新时间 | 2024-05-02 23:58:10 | ||
图片预览



文档简介
2024年初中科学重点题型复习--浮力计算题
1.如图所示,圆柱形容器内盛有一定量的水,一实心正方体木块漂浮在水面上,已知木块的体积为1000cm3,ρ木=0.6×103kg/m3,求:
(1)木块受到的浮力;
(2)木块排开水的体积;
(3)若要使木块刚好浸没在水中,必须给木块一个竖直向下多大的压力?
2.重力不计的轻杆AOB可绕支点О无摩擦转动,当把甲乙两物体如下图所示分别挂在两个端点A、B上时,轻杆恰好在水平位置平衡,此时乙物体刚好完全浸没在装有水的容器里且水未溢出,物体乙未与容器底接触,已知轻杆长2.1m,支点O距端点B的距离为1.4m,物体甲的质量为27.6kg,物体乙的体积为0.002m3。(忽略绳重)
求:(1)弹簧测力计的示数;
(2)乙物体的密度。
3.如图所示,将一个长、宽、高分别为5cm、4cm、12cm的长方体实心铁块,直立放在溢水杯底(铁块与杯底不密合)。向溢水杯内缓慢注水,当溢水杯中的水面与溢水口相平时水深8cm。已知水的密度,取,求:
(1)水对溢水杯底产生的压强大小p;
(2)铁块所受的浮力大小;
(3)若仅将铁块换为形状完全相同、质量为144g的木块,请通过计算说明木块在水中能否保持立在杯底。
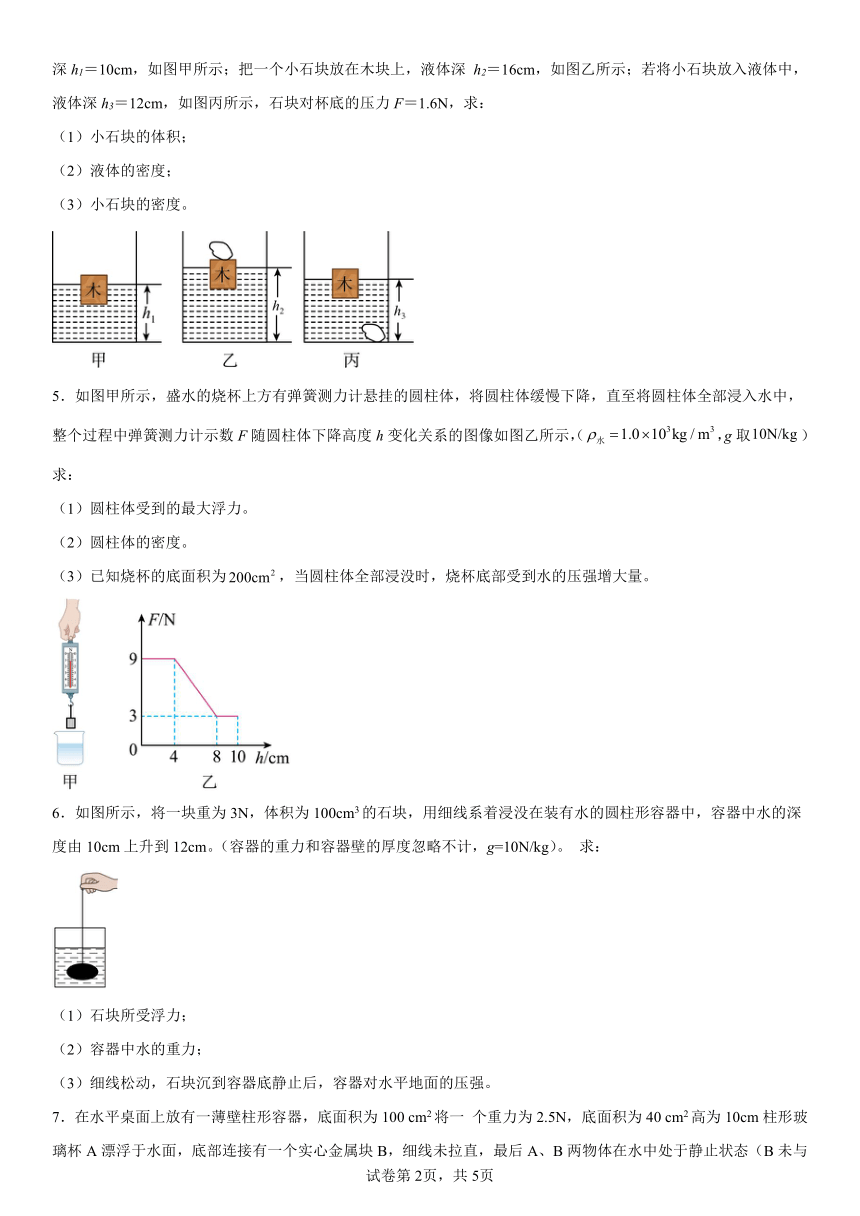
4.一个底面积为50cm2的烧杯中装有某种液体(液体密度未知),将一个木块放入烧杯的液体中,木块静止时液体深h1=10cm,如图甲所示;把一个小石块放在木块上,液体深 h2=16cm,如图乙所示;若将小石块放入液体中,液体深h3=12cm,如图丙所示,石块对杯底的压力F=1.6N,求:
(1)小石块的体积;
(2)液体的密度;
(3)小石块的密度。
5.如图甲所示,盛水的烧杯上方有弹簧测力计悬挂的圆柱体,将圆柱体缓慢下降,直至将圆柱体全部浸入水中,整个过程中弹簧测力计示数F随圆柱体下降高度h变化关系的图像如图乙所示,(,g取)求:
(1)圆柱体受到的最大浮力。
(2)圆柱体的密度。
(3)已知烧杯的底面积为,当圆柱体全部浸没时,烧杯底部受到水的压强增大量。
6.如图所示,将一块重为3N,体积为100cm3的石块,用细线系着浸没在装有水的圆柱形容器中,容器中水的深度由10cm上升到12cm。(容器的重力和容器壁的厚度忽略不计,g=10N/kg)。 求:
(1)石块所受浮力;
(2)容器中水的重力;
(3)细线松动,石块沉到容器底静止后,容器对水平地面的压强。
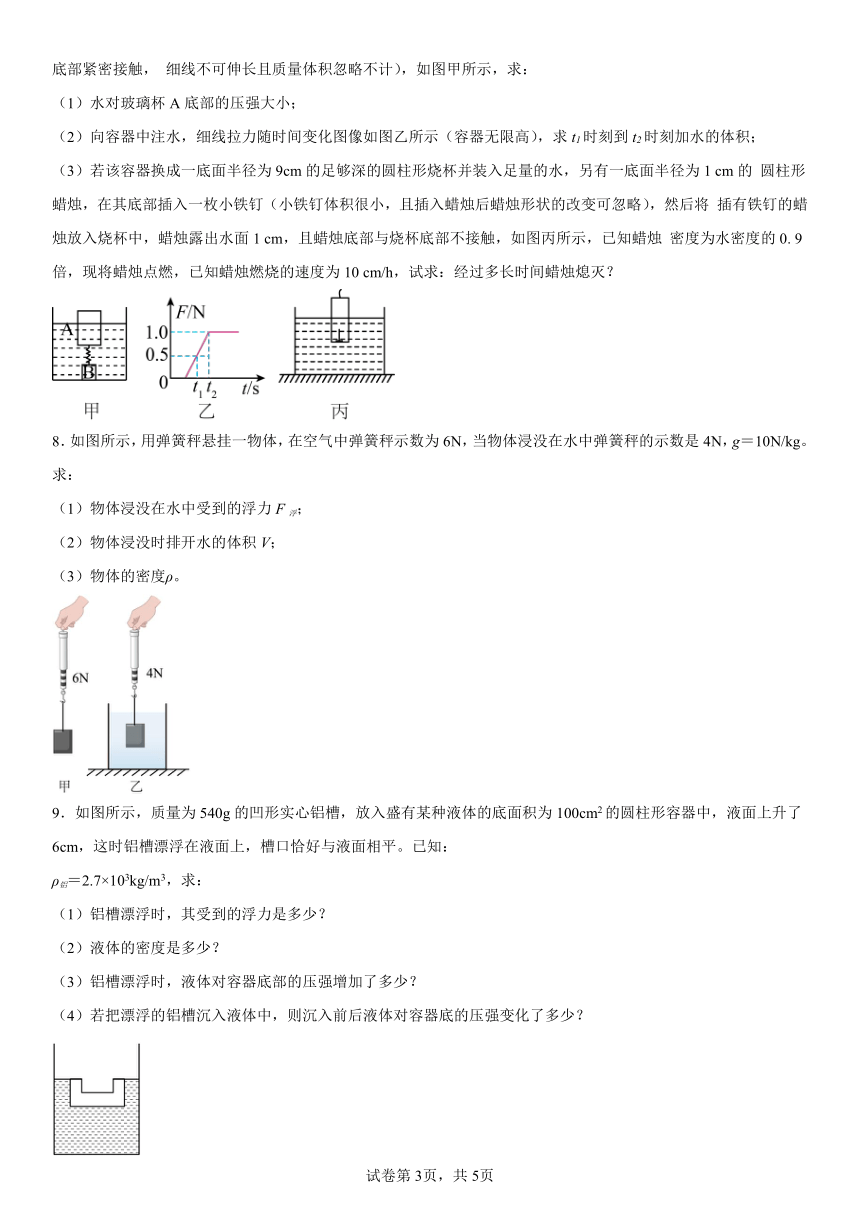
7.在水平桌面上放有一薄壁柱形容器,底面积为100 cm2将一 个重力为2.5N,底面积为40 cm2高为10cm柱形玻璃杯A漂浮于水面,底部连接有一个实心金属块B,细线未拉直,最后A、B两物体在水中处于静止状态(B未与底部紧密接触, 细线不可伸长且质量体积忽略不计),如图甲所示,求:
(1)水对玻璃杯A底部的压强大小;
(2)向容器中注水,细线拉力随时间变化图像如图乙所示(容器无限高),求t1时刻到t2时刻加水的体积;
(3)若该容器换成一底面半径为9cm的足够深的圆柱形烧杯并装入足量的水,另有一底面半径为1 cm的 圆柱形蜡烛,在其底部插入一枚小铁钉(小铁钉体积很小,且插入蜡烛后蜡烛形状的改变可忽略),然后将 插有铁钉的蜡烛放入烧杯中,蜡烛露出水面1 cm,且蜡烛底部与烧杯底部不接触,如图丙所示,已知蜡烛 密度为水密度的0. 9倍,现将蜡烛点燃,已知蜡烛燃烧的速度为10 cm/h,试求:经过多长时间蜡烛熄灭?
8.如图所示,用弹簧秤悬挂一物体,在空气中弹簧秤示数为6N,当物体浸没在水中弹簧秤的示数是4N,g=10N/kg。求:
(1)物体浸没在水中受到的浮力F浮;
(2)物体浸没时排开水的体积V;
(3)物体的密度ρ。
9.如图所示,质量为540g的凹形实心铝槽,放入盛有某种液体的底面积为100cm2的圆柱形容器中,液面上升了6cm,这时铝槽漂浮在液面上,槽口恰好与液面相平。已知:
ρ铝=2.7×103kg/m3,求:
(1)铝槽漂浮时,其受到的浮力是多少?
(2)液体的密度是多少?
(3)铝槽漂浮时,液体对容器底部的压强增加了多少?
(4)若把漂浮的铝槽沉入液体中,则沉入前后液体对容器底的压强变化了多少?
10.如图所示,将一个体积为、重6N的木块用细线系在底面积为400cm2的圆柱形容器的底部。当容器中倒入足够的水使木块被浸没时,水的深度为30cm。求:(g取10N/kg)
(1)水对容器底部的压强;
(2)木块浸没在水中受到的浮力;
(3)剪断细线后,木块处于静止时露出水面的体积多大。
11.如图所示,柱形容器内水深10cm,水中形状完全相同的A、B两个长方体通过底部的定滑轮用细线相连,物体B上表面与水面相平,如图甲所示物体A有体积露出水面,物体A质量为0.2kg,物体B质量为0.6kg,求:
(1)容器底部受到水的压强;
(2)A与B物体密度的比值;
(3)物体B受到的浮力。
12.如图所示,这是一种简易温度计,在不同环境温度下小球浸没在液体中的位置和悬挂的金属链条长度会发生改变,指针指示温度值,已知温度计中小球重为1.2 N,体积为200cm3(小球体积变化可忽略),金属链条受到的浮力忽略不计,30℃时容器内液体密度为0.8×103kg/m3,g取10 N/kg。
(1)30 ℃时小球受到的浮力为多少
(2)在某一温度时,拉起链条的质量为60g,此时液体的密度为多少
(3)已知容器的底面积为200cm2,30℃时若链条在外力作用下与小球分离,小球静止后液体对容器底部的压强与未分离前相比变化了多少
13.如图甲所示,均匀圆柱体A和薄壁圆柱形容器B置于水平地面上,容器B的底面积为2×10-2m2,其内部盛有0.2m深的水,g=10N/kg,ρ=1×103kg/m 。求:
(1)容器中水的重力;
(2)水对容器底部的压强;
(3)现将A浸没在容器B的水中(水未溢出),如图乙所示。水对容器底部压强的增加量为1000Pa,求水面上升的高度。
14.如图所示的储水容器中有质量为0.5kg,底面积为100cm2,高42cm的圆柱体浮桶,轻质弹簧的下端与桶连接,上端与绝缘片A连接,绝缘片A固定在支架上不动,距容器底0.4m处的侧壁有排水阀门。容器内无水时,弹簧与浮桶间没有力的作用。当桶底升至阀门所处高度时,绝缘片A受到弹簧的力为15N,阀门打开,开始排水,弹簧均在弹性限度内。求:
(1)浮桶的重力是多少N?
(2)开始排水时,浮桶所受浮力为多大?
(3)储水容器的底面积为5000cm2,开始排水时,容器底受到水的压力为多大?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.(1)6N;(2);(3)4N
【详解】解:(1)因为木块漂浮,在竖直方向上木块处于平衡状态,受平衡力,由平衡条件得
(2)木块排开水的体积,由阿基米德原理得
(3)木块浸没后受到的浮力,根据阿基米德原理,则
若木块刚好浸没在水中静止,对木块做受力分析可得
则需要施加的力
答:(1)木块受到的浮力是6N;
(2)木块排开水的体积是;
(3)若要使木块刚好浸没在水中,必须给木块一个竖直向下4N的压力。
2.(1)138N (2)
【详解】(1)甲对A点向下的拉力等于重力为
FA=G甲=m甲g=27.6kg×10N/kg=276N
由杠杆平衡公式可求B点对绳子向上的拉力为
由于弹簧测力计处于平衡状态,则下端拉力为138N,故示数为138N。
(2)乙浸没,排开液体体积与物体体积相同,则受到的浮力为
乙受力平衡,则乙的重力为
G乙=F乙浮+F弹=20N+138N=158N
则乙的密度为
3.(1)800Pa;(2);(3)见解析
【详解】解:(1)当溢水杯中的水面与溢水口相平时水深为
h=8cm=0.08m
水对溢水杯底产生的压强为
(2)由题意知,铁块此时排开水的体积为
根据阿基米德原理,铁块所受的浮力为
(3)将铁块换为形状完全相同、质量为144g的木块,由可得,木块的重力为
假设木块能保持立在水底,则所受浮力为F浮′=1.6N,由于
F浮′>G
即,木块受到的浮力大于木块自身的重力,故木块会漂浮,所以木块在水中不能保持立在杯底。
答:(1)水对溢水杯底产生的压强大小p为800Pa;
(2)铁块所受的浮力大小F浮为1.6N;
(3)木块在水中不能保持立在杯底,计算过程见解答过程。
4.(1)1×10-4m3;(2)0.8×103kg/m3;(3)2.4×103kg/m3
【详解】解:(1)由丙、甲两图可知,小石块的体积
V石=(h3-h1)S=(0.12m-0.1m)×50×10-4m2=1×10-4m3
(2)由乙、甲图可知,石块放在木块上时比木块多排开液体的体积
ΔV排=(h2-h1)S=(0.16m-0.1m)×50×10-4m2=3×10-4m3
木块受到的浮力差
ΔF=ρ液gΔV排=ρ液×10N/kg×3×10-4m3
因为木块和石块放在木块上时木块漂浮,所以石块的重力
G石=m石g=ΔF=ρ液×10N/kg×3×10-4m3
在图丙中,石块受到的浮力
F浮丙=ρ液gV石=ρ液×10N/kg×1×10-4m3
小石块对杯底的压力
F=G石-F浮丙=ρ液×10N/kg×3×10-4m3-ρ液×10N/kg×1×10-4m3=1.6N
解得ρ液=0.8×103kg/m3。
(3)小石块的重力
G石=0.8×103kg/m3×10N/kg×3×10-4m3=2.4N
小石块的密度
=2.4×103kg/m3。
答:(1)小石块的体积为1×10-4m3;
(2)液体的密度为0.8×103kg/m3;
(3)小石块的密度为2.4×103kg/m3。
5.(1);(2);(3)
【详解】解:(1)由图像可知,下降时物体在空气中,因圆柱体缓慢下降,圆柱体受到的重力
图像中下降时圆柱体完全浸入水中此时圆柱体受到的拉力,则圆柱体受到的最大浮力
(2)由可得,物体的体积
物体的质量
圆柱体的密度
(3)当圆柱体全部浸没时,杯内液体深度的增加量
烧杯底部受到水的压强的增加量
答:(1)圆柱体受到的最大浮力为;
(2)圆柱体的密度为;
(3)当圆柱体全部浸没时,烧杯底部受到水的压强增大量为。
6.(1)1N;(2)5N;(3)1.6×103Pa
【详解】解:(1)体积为100cm3的石块,浸没在圆柱形容器中,排开水的体积是石块的体积,则石块所受浮力
F浮=ρ液gV排=1×103kg/m3×10N/kg×100×10-6m3=1N
(2)容器底面积
容器中水的体积
V水=Sh=50cm2×10cm=5×102cm3
则水的重力
G水=m水g=ρ水gV水=1×103kg/m3×10N/kg×5×102×10-6m3=5N
(3)容器对水平地面压强为
答:(1)石块所受浮力为1N;
(2)容器中水的重力为5N;
(3)容器对水平地面的压强为1.6×103Pa。
7.(1)625Pa;(2)75cm3;(3)1h
【详解】解:(1)玻璃杯A重力为2.5N,漂浮于水面, 重力与浮力相等,浮力等于杯底水的压力
水对玻璃杯A底部的压强
(2)杯重2.5N, t1时刻,细线拉力0.5N,此时浮力
A浸在液体中的体积
A浸在液体中的深度
t2时刻,细线拉力1N,此时浮力
A浸在液体中的体积
A浸在液体中的深度
加入的水深为
加入水的体积
(3)蜡烛露出水面1 cm,处于漂浮,浮力与重力相等
可求得钉子重力
①
蜡烛熄灭时,即蜡烛上表面刚好没入水里时,此时蜡烛长度h1,蜡烛与铁钉构成的整体平均密度与水的密度相同
②
将①代入②
整理得
蜡烛燃烧的长度
而蜡烛燃烧的速度为10cm/h,故蜡烛可燃烧1h。
答:(1) 水对玻璃杯A底部的压强625Pa;
(2)t1时刻到t2时刻加水的体积75cm3;
(3)经过1h蜡烛熄灭。
8.(1)2N;(2);(3)
【详解】解:(1)物体浸没在水中受到的浮力
(2)由 可得,物体浸没时排开水的体积
(3)由可得,物体的质量
因物体浸没时排开液体的体积和自身的体积相等,所以,物体的密度
答:(1)物体浸没在水中受到的浮力为2N;
(2)物体浸没时排开水的体积为;
(3)物体的密度为。
9.(1)5.4N;(2)0.9×103kg/m3;(3)540Pa;(4)360Pa
【详解】解:(1)实心铝槽的质量为
铝槽漂浮,铝槽受到的浮力
(2)由题知,铝槽排开水的体积
根据可知液体的密度
(3)铝槽漂浮时,液体对容器底部的压强增加量
(4)铝槽浸没时排开水的体积
液面上升的高度
沉入前后液面变化值
沉入前后液体对容器底的压强变化值
答:(1)铝槽漂浮时,其受到的浮力是5.4N;
(2)液体的密度是0.9×103kg/m3;
(3)铝槽漂浮时,液体对容器底部的压强增加了540Pa;
(4)若把漂浮的铝槽沉入液体中,则沉入前后液体对容器底的压强变化了360Pa。
10.(1);(2)10N;(3)
【详解】解:(1)水对容器底部的压强
(2)木块浸没在水中时排开水的体积等于木块的体积,此时木块受到的浮力
(3)因为木块受到的浮力大于木块的重力,所以剪断细线后,木块将上浮,静止时漂浮在水面上,受到浮力
木块浸入水中的体积
则其露出水面的体积
答:(1)水对容器底部的压强为;
(2)木块浸没在水中受到的浮力为10N;
(3)剪断细线后,木块处于静止时露出水面的体积为。
11.(1)1000Pa;(2)1:3;(3)12N
【详解】解:(1)容器底部受到水的压强
(2)根据题意可知,物体A与B的体积相等,即VA=VB,A与B物体密度的比值
(3)对物体A受力分析可知,物体A受到竖直向下的重力、竖直向下的拉力以及竖直向上的浮力作用,物体A在这三个力的作用下保持静止,则
……①
同理,对物体B受力分析可知
……②
假设物体A与B的体积均为V,根据阿基米德原理可知,物体B受到的浮力:F浮B=ρgV,物体A受到的浮力
则
……③
联立①②③可得
答:(1)容器底部受到水的压强为1000Pa;
(2)A与B物体密度的比值为1∶3;
(3)物体B受到的浮力为12N。
12.(1)1.6N;(2)0.9×103kg/m3;(3)20Pa
【详解】
(1)30 ℃时小球受到的浮力
(2)小球静止时处于悬浮状态,因此小球悬浮时受到的浮力等于自身重力和链条的重力之和,所以小球受到的浮力
液体的密度
(3)小球浸没在30℃液体中时所受的浮力大于小球自重,链条与小球分离后小球将漂浮在液面上,静止时受到的浮力等于小球自重,此时小球排开液体的条件
小球静止在液面上时的液面高度对比分离前液面的高度变化
压强的变化量
答:(1)30 ℃时小球受到的浮力为1.6N;
(2)在某一温度时,拉起链条的质量为60g,此时液体的密度为0.9×103kg/m3;
(3)已知容器的底面积为200cm2,30℃时若链条在外力作用下与小球分离,小球静止后液体对容器底部的压强与未分离前相比变化了20Pa。
13.(1)40N;(2)2×103Pa;(3)0.1m
【详解】解:(1)容器中水的体积
容器中水的重力
(2)水对容器底部的压强
(3)圆柱体A放入水中后,容器B中水面升高量
答:(1)容器中水的重力为40N;
(2)水对容器底部的压强为2×103Pa;
(3)水面上升的高度为0.1m。
14.(1)5N;(2)20N;(3)3×103 N
【详解】解:(1)浮桶的重力为
(2)当桶底升至阀门所处高度时,绝缘片受到弹簧的力为,根据物体间力的作用是相互的,所以弹簧给浮桶向下的压力也是,浮桶受到竖直向上的浮力、竖直向下的重力和压力,这三个力平衡,则此时浮桶受到的浮力为
(3)浮桶排开水的体积为
则浮桶浸入水中的深度为
此时容器内水的深度为
容器底受到水的压强为
容器底受到水的压力为
答:(1)浮桶的重力是;
(2)开始排水时,浮桶所受浮力为;
(3)储水容器的底面积为,开始排水时,容器底受到水的压力为。
答案第1页,共2页
答案第1页,共2页
1.如图所示,圆柱形容器内盛有一定量的水,一实心正方体木块漂浮在水面上,已知木块的体积为1000cm3,ρ木=0.6×103kg/m3,求:
(1)木块受到的浮力;
(2)木块排开水的体积;
(3)若要使木块刚好浸没在水中,必须给木块一个竖直向下多大的压力?
2.重力不计的轻杆AOB可绕支点О无摩擦转动,当把甲乙两物体如下图所示分别挂在两个端点A、B上时,轻杆恰好在水平位置平衡,此时乙物体刚好完全浸没在装有水的容器里且水未溢出,物体乙未与容器底接触,已知轻杆长2.1m,支点O距端点B的距离为1.4m,物体甲的质量为27.6kg,物体乙的体积为0.002m3。(忽略绳重)
求:(1)弹簧测力计的示数;
(2)乙物体的密度。
3.如图所示,将一个长、宽、高分别为5cm、4cm、12cm的长方体实心铁块,直立放在溢水杯底(铁块与杯底不密合)。向溢水杯内缓慢注水,当溢水杯中的水面与溢水口相平时水深8cm。已知水的密度,取,求:
(1)水对溢水杯底产生的压强大小p;
(2)铁块所受的浮力大小;
(3)若仅将铁块换为形状完全相同、质量为144g的木块,请通过计算说明木块在水中能否保持立在杯底。
4.一个底面积为50cm2的烧杯中装有某种液体(液体密度未知),将一个木块放入烧杯的液体中,木块静止时液体深h1=10cm,如图甲所示;把一个小石块放在木块上,液体深 h2=16cm,如图乙所示;若将小石块放入液体中,液体深h3=12cm,如图丙所示,石块对杯底的压力F=1.6N,求:
(1)小石块的体积;
(2)液体的密度;
(3)小石块的密度。
5.如图甲所示,盛水的烧杯上方有弹簧测力计悬挂的圆柱体,将圆柱体缓慢下降,直至将圆柱体全部浸入水中,整个过程中弹簧测力计示数F随圆柱体下降高度h变化关系的图像如图乙所示,(,g取)求:
(1)圆柱体受到的最大浮力。
(2)圆柱体的密度。
(3)已知烧杯的底面积为,当圆柱体全部浸没时,烧杯底部受到水的压强增大量。
6.如图所示,将一块重为3N,体积为100cm3的石块,用细线系着浸没在装有水的圆柱形容器中,容器中水的深度由10cm上升到12cm。(容器的重力和容器壁的厚度忽略不计,g=10N/kg)。 求:
(1)石块所受浮力;
(2)容器中水的重力;
(3)细线松动,石块沉到容器底静止后,容器对水平地面的压强。
7.在水平桌面上放有一薄壁柱形容器,底面积为100 cm2将一 个重力为2.5N,底面积为40 cm2高为10cm柱形玻璃杯A漂浮于水面,底部连接有一个实心金属块B,细线未拉直,最后A、B两物体在水中处于静止状态(B未与底部紧密接触, 细线不可伸长且质量体积忽略不计),如图甲所示,求:
(1)水对玻璃杯A底部的压强大小;
(2)向容器中注水,细线拉力随时间变化图像如图乙所示(容器无限高),求t1时刻到t2时刻加水的体积;
(3)若该容器换成一底面半径为9cm的足够深的圆柱形烧杯并装入足量的水,另有一底面半径为1 cm的 圆柱形蜡烛,在其底部插入一枚小铁钉(小铁钉体积很小,且插入蜡烛后蜡烛形状的改变可忽略),然后将 插有铁钉的蜡烛放入烧杯中,蜡烛露出水面1 cm,且蜡烛底部与烧杯底部不接触,如图丙所示,已知蜡烛 密度为水密度的0. 9倍,现将蜡烛点燃,已知蜡烛燃烧的速度为10 cm/h,试求:经过多长时间蜡烛熄灭?
8.如图所示,用弹簧秤悬挂一物体,在空气中弹簧秤示数为6N,当物体浸没在水中弹簧秤的示数是4N,g=10N/kg。求:
(1)物体浸没在水中受到的浮力F浮;
(2)物体浸没时排开水的体积V;
(3)物体的密度ρ。
9.如图所示,质量为540g的凹形实心铝槽,放入盛有某种液体的底面积为100cm2的圆柱形容器中,液面上升了6cm,这时铝槽漂浮在液面上,槽口恰好与液面相平。已知:
ρ铝=2.7×103kg/m3,求:
(1)铝槽漂浮时,其受到的浮力是多少?
(2)液体的密度是多少?
(3)铝槽漂浮时,液体对容器底部的压强增加了多少?
(4)若把漂浮的铝槽沉入液体中,则沉入前后液体对容器底的压强变化了多少?
10.如图所示,将一个体积为、重6N的木块用细线系在底面积为400cm2的圆柱形容器的底部。当容器中倒入足够的水使木块被浸没时,水的深度为30cm。求:(g取10N/kg)
(1)水对容器底部的压强;
(2)木块浸没在水中受到的浮力;
(3)剪断细线后,木块处于静止时露出水面的体积多大。
11.如图所示,柱形容器内水深10cm,水中形状完全相同的A、B两个长方体通过底部的定滑轮用细线相连,物体B上表面与水面相平,如图甲所示物体A有体积露出水面,物体A质量为0.2kg,物体B质量为0.6kg,求:
(1)容器底部受到水的压强;
(2)A与B物体密度的比值;
(3)物体B受到的浮力。
12.如图所示,这是一种简易温度计,在不同环境温度下小球浸没在液体中的位置和悬挂的金属链条长度会发生改变,指针指示温度值,已知温度计中小球重为1.2 N,体积为200cm3(小球体积变化可忽略),金属链条受到的浮力忽略不计,30℃时容器内液体密度为0.8×103kg/m3,g取10 N/kg。
(1)30 ℃时小球受到的浮力为多少
(2)在某一温度时,拉起链条的质量为60g,此时液体的密度为多少
(3)已知容器的底面积为200cm2,30℃时若链条在外力作用下与小球分离,小球静止后液体对容器底部的压强与未分离前相比变化了多少
13.如图甲所示,均匀圆柱体A和薄壁圆柱形容器B置于水平地面上,容器B的底面积为2×10-2m2,其内部盛有0.2m深的水,g=10N/kg,ρ=1×103kg/m 。求:
(1)容器中水的重力;
(2)水对容器底部的压强;
(3)现将A浸没在容器B的水中(水未溢出),如图乙所示。水对容器底部压强的增加量为1000Pa,求水面上升的高度。
14.如图所示的储水容器中有质量为0.5kg,底面积为100cm2,高42cm的圆柱体浮桶,轻质弹簧的下端与桶连接,上端与绝缘片A连接,绝缘片A固定在支架上不动,距容器底0.4m处的侧壁有排水阀门。容器内无水时,弹簧与浮桶间没有力的作用。当桶底升至阀门所处高度时,绝缘片A受到弹簧的力为15N,阀门打开,开始排水,弹簧均在弹性限度内。求:
(1)浮桶的重力是多少N?
(2)开始排水时,浮桶所受浮力为多大?
(3)储水容器的底面积为5000cm2,开始排水时,容器底受到水的压力为多大?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.(1)6N;(2);(3)4N
【详解】解:(1)因为木块漂浮,在竖直方向上木块处于平衡状态,受平衡力,由平衡条件得
(2)木块排开水的体积,由阿基米德原理得
(3)木块浸没后受到的浮力,根据阿基米德原理,则
若木块刚好浸没在水中静止,对木块做受力分析可得
则需要施加的力
答:(1)木块受到的浮力是6N;
(2)木块排开水的体积是;
(3)若要使木块刚好浸没在水中,必须给木块一个竖直向下4N的压力。
2.(1)138N (2)
【详解】(1)甲对A点向下的拉力等于重力为
FA=G甲=m甲g=27.6kg×10N/kg=276N
由杠杆平衡公式可求B点对绳子向上的拉力为
由于弹簧测力计处于平衡状态,则下端拉力为138N,故示数为138N。
(2)乙浸没,排开液体体积与物体体积相同,则受到的浮力为
乙受力平衡,则乙的重力为
G乙=F乙浮+F弹=20N+138N=158N
则乙的密度为
3.(1)800Pa;(2);(3)见解析
【详解】解:(1)当溢水杯中的水面与溢水口相平时水深为
h=8cm=0.08m
水对溢水杯底产生的压强为
(2)由题意知,铁块此时排开水的体积为
根据阿基米德原理,铁块所受的浮力为
(3)将铁块换为形状完全相同、质量为144g的木块,由可得,木块的重力为
假设木块能保持立在水底,则所受浮力为F浮′=1.6N,由于
F浮′>G
即,木块受到的浮力大于木块自身的重力,故木块会漂浮,所以木块在水中不能保持立在杯底。
答:(1)水对溢水杯底产生的压强大小p为800Pa;
(2)铁块所受的浮力大小F浮为1.6N;
(3)木块在水中不能保持立在杯底,计算过程见解答过程。
4.(1)1×10-4m3;(2)0.8×103kg/m3;(3)2.4×103kg/m3
【详解】解:(1)由丙、甲两图可知,小石块的体积
V石=(h3-h1)S=(0.12m-0.1m)×50×10-4m2=1×10-4m3
(2)由乙、甲图可知,石块放在木块上时比木块多排开液体的体积
ΔV排=(h2-h1)S=(0.16m-0.1m)×50×10-4m2=3×10-4m3
木块受到的浮力差
ΔF=ρ液gΔV排=ρ液×10N/kg×3×10-4m3
因为木块和石块放在木块上时木块漂浮,所以石块的重力
G石=m石g=ΔF=ρ液×10N/kg×3×10-4m3
在图丙中,石块受到的浮力
F浮丙=ρ液gV石=ρ液×10N/kg×1×10-4m3
小石块对杯底的压力
F=G石-F浮丙=ρ液×10N/kg×3×10-4m3-ρ液×10N/kg×1×10-4m3=1.6N
解得ρ液=0.8×103kg/m3。
(3)小石块的重力
G石=0.8×103kg/m3×10N/kg×3×10-4m3=2.4N
小石块的密度
=2.4×103kg/m3。
答:(1)小石块的体积为1×10-4m3;
(2)液体的密度为0.8×103kg/m3;
(3)小石块的密度为2.4×103kg/m3。
5.(1);(2);(3)
【详解】解:(1)由图像可知,下降时物体在空气中,因圆柱体缓慢下降,圆柱体受到的重力
图像中下降时圆柱体完全浸入水中此时圆柱体受到的拉力,则圆柱体受到的最大浮力
(2)由可得,物体的体积
物体的质量
圆柱体的密度
(3)当圆柱体全部浸没时,杯内液体深度的增加量
烧杯底部受到水的压强的增加量
答:(1)圆柱体受到的最大浮力为;
(2)圆柱体的密度为;
(3)当圆柱体全部浸没时,烧杯底部受到水的压强增大量为。
6.(1)1N;(2)5N;(3)1.6×103Pa
【详解】解:(1)体积为100cm3的石块,浸没在圆柱形容器中,排开水的体积是石块的体积,则石块所受浮力
F浮=ρ液gV排=1×103kg/m3×10N/kg×100×10-6m3=1N
(2)容器底面积
容器中水的体积
V水=Sh=50cm2×10cm=5×102cm3
则水的重力
G水=m水g=ρ水gV水=1×103kg/m3×10N/kg×5×102×10-6m3=5N
(3)容器对水平地面压强为
答:(1)石块所受浮力为1N;
(2)容器中水的重力为5N;
(3)容器对水平地面的压强为1.6×103Pa。
7.(1)625Pa;(2)75cm3;(3)1h
【详解】解:(1)玻璃杯A重力为2.5N,漂浮于水面, 重力与浮力相等,浮力等于杯底水的压力
水对玻璃杯A底部的压强
(2)杯重2.5N, t1时刻,细线拉力0.5N,此时浮力
A浸在液体中的体积
A浸在液体中的深度
t2时刻,细线拉力1N,此时浮力
A浸在液体中的体积
A浸在液体中的深度
加入的水深为
加入水的体积
(3)蜡烛露出水面1 cm,处于漂浮,浮力与重力相等
可求得钉子重力
①
蜡烛熄灭时,即蜡烛上表面刚好没入水里时,此时蜡烛长度h1,蜡烛与铁钉构成的整体平均密度与水的密度相同
②
将①代入②
整理得
蜡烛燃烧的长度
而蜡烛燃烧的速度为10cm/h,故蜡烛可燃烧1h。
答:(1) 水对玻璃杯A底部的压强625Pa;
(2)t1时刻到t2时刻加水的体积75cm3;
(3)经过1h蜡烛熄灭。
8.(1)2N;(2);(3)
【详解】解:(1)物体浸没在水中受到的浮力
(2)由 可得,物体浸没时排开水的体积
(3)由可得,物体的质量
因物体浸没时排开液体的体积和自身的体积相等,所以,物体的密度
答:(1)物体浸没在水中受到的浮力为2N;
(2)物体浸没时排开水的体积为;
(3)物体的密度为。
9.(1)5.4N;(2)0.9×103kg/m3;(3)540Pa;(4)360Pa
【详解】解:(1)实心铝槽的质量为
铝槽漂浮,铝槽受到的浮力
(2)由题知,铝槽排开水的体积
根据可知液体的密度
(3)铝槽漂浮时,液体对容器底部的压强增加量
(4)铝槽浸没时排开水的体积
液面上升的高度
沉入前后液面变化值
沉入前后液体对容器底的压强变化值
答:(1)铝槽漂浮时,其受到的浮力是5.4N;
(2)液体的密度是0.9×103kg/m3;
(3)铝槽漂浮时,液体对容器底部的压强增加了540Pa;
(4)若把漂浮的铝槽沉入液体中,则沉入前后液体对容器底的压强变化了360Pa。
10.(1);(2)10N;(3)
【详解】解:(1)水对容器底部的压强
(2)木块浸没在水中时排开水的体积等于木块的体积,此时木块受到的浮力
(3)因为木块受到的浮力大于木块的重力,所以剪断细线后,木块将上浮,静止时漂浮在水面上,受到浮力
木块浸入水中的体积
则其露出水面的体积
答:(1)水对容器底部的压强为;
(2)木块浸没在水中受到的浮力为10N;
(3)剪断细线后,木块处于静止时露出水面的体积为。
11.(1)1000Pa;(2)1:3;(3)12N
【详解】解:(1)容器底部受到水的压强
(2)根据题意可知,物体A与B的体积相等,即VA=VB,A与B物体密度的比值
(3)对物体A受力分析可知,物体A受到竖直向下的重力、竖直向下的拉力以及竖直向上的浮力作用,物体A在这三个力的作用下保持静止,则
……①
同理,对物体B受力分析可知
……②
假设物体A与B的体积均为V,根据阿基米德原理可知,物体B受到的浮力:F浮B=ρgV,物体A受到的浮力
则
……③
联立①②③可得
答:(1)容器底部受到水的压强为1000Pa;
(2)A与B物体密度的比值为1∶3;
(3)物体B受到的浮力为12N。
12.(1)1.6N;(2)0.9×103kg/m3;(3)20Pa
【详解】
(1)30 ℃时小球受到的浮力
(2)小球静止时处于悬浮状态,因此小球悬浮时受到的浮力等于自身重力和链条的重力之和,所以小球受到的浮力
液体的密度
(3)小球浸没在30℃液体中时所受的浮力大于小球自重,链条与小球分离后小球将漂浮在液面上,静止时受到的浮力等于小球自重,此时小球排开液体的条件
小球静止在液面上时的液面高度对比分离前液面的高度变化
压强的变化量
答:(1)30 ℃时小球受到的浮力为1.6N;
(2)在某一温度时,拉起链条的质量为60g,此时液体的密度为0.9×103kg/m3;
(3)已知容器的底面积为200cm2,30℃时若链条在外力作用下与小球分离,小球静止后液体对容器底部的压强与未分离前相比变化了20Pa。
13.(1)40N;(2)2×103Pa;(3)0.1m
【详解】解:(1)容器中水的体积
容器中水的重力
(2)水对容器底部的压强
(3)圆柱体A放入水中后,容器B中水面升高量
答:(1)容器中水的重力为40N;
(2)水对容器底部的压强为2×103Pa;
(3)水面上升的高度为0.1m。
14.(1)5N;(2)20N;(3)3×103 N
【详解】解:(1)浮桶的重力为
(2)当桶底升至阀门所处高度时,绝缘片受到弹簧的力为,根据物体间力的作用是相互的,所以弹簧给浮桶向下的压力也是,浮桶受到竖直向上的浮力、竖直向下的重力和压力,这三个力平衡,则此时浮桶受到的浮力为
(3)浮桶排开水的体积为
则浮桶浸入水中的深度为
此时容器内水的深度为
容器底受到水的压强为
容器底受到水的压力为
答:(1)浮桶的重力是;
(2)开始排水时,浮桶所受浮力为;
(3)储水容器的底面积为,开始排水时,容器底受到水的压力为。
答案第1页,共2页
答案第1页,共2页
