4.3比例的应用(课件)-六年级下册数学人教版(共46张PPT)
文档属性
| 名称 | 4.3比例的应用(课件)-六年级下册数学人教版(共46张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-05 16:10:51 | ||
图片预览











文档简介
(共46张PPT)
4 比例
3.比例的应用
数学人教版六年级下册
第1课时 用比例解决问题(1)
进一步理解正比例的意义,掌握用正比例知识解决问题的方法与步骤。
正确利用正比例知识列出方程,解决生活中简单的实际问题。
学习目标
【重点】
利用正比例关系列出含有未知数的等式,运用正比例知识正确解决问题。
【难点】
掌握用正比例知识解答应用题的步骤和
方法。
课堂导入
判断下列每题中的两种量是否成比例关系,成什么比例关系?
(1)已知A÷B=C。
当A一定时,B和C成( )比例关系。
当B一定时,A和C成( )比例关系。
当C一定时,A和B成( )比例关系。
反
正
正
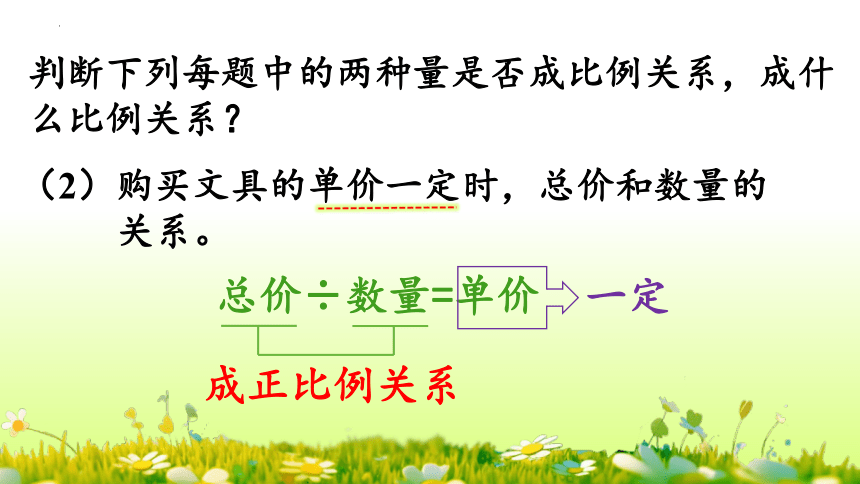
(2)购买文具的单价一定时,总价和数量的
关系。
总价÷数量=单价
成正比例关系
判断下列每题中的两种量是否成比例关系,成什么比例关系?
一定
用水量
水费
用水量
新知探究
张阿姨家上个月用了8 t水,水费是40元。李奶奶家上个月用了10 t水,李奶奶家上个月的水费是多少?
教材第59页例5
你能从题中获取哪些信息?
5
用户 上个月用水量 水费
张阿姨家
李奶奶家
8 t
40元
10 t
?元
张阿姨家上个月用了8 t水,水费是40元。李奶奶家上个月用了10 t水,李奶奶家上个月的水费是多少?
教材第59页例5
5
张阿姨家上个月用了8 t水,水费是40元。李奶奶家上个月用了10 t水,李奶奶家上个月的水费是多少?
教材第59页例5
5
这些量成什么数量关系?
水费÷用水量=水的单价
一定
成正比例关系
教材第59页例5
方法一:我先算出每吨水的价钱,再算10 t水多少钱。
答:李奶奶家上个月的水费是。
=
教材第59页例5
方法二:还可以用比例的方法解决。
每吨水的价钱一定,所以水费和用水吨数成正比例关系。
两家的水费和用水吨数的比值相等。
教材第59页例5
解:设李奶奶家上个月的水费是x元。
=
8x = 40×10
x = 50
x =
=
还可以这样列式:
=
8x = 40×10
x = 50
请你总结出解决本题的方法。
解这个问题的关键是找到不变的量。
1
只要两个量的比值一定,就可以用正比例关系解答。
2
虽然未知量变了,但题中水费和用水的吨数的正比例关系没变。
问题延伸
王爷爷家上个月的水费是60元,他家上个月用了多少吨水?
问题延伸
王爷爷家上个月的水费是60元,他家上个月用了多少吨水?
解:设他家上个月用了x吨水。
答:他家上个月用了12吨水。
课堂练习
1.小明买4支圆珠笔用了6元。小刚想买3支同样
的圆珠笔,要用多少钱?
教材第60页“做一做”第1题
圆珠笔的单价不变。
解:设买3支同样的圆珠笔,要用x元。
答:买3支同样的圆珠笔,要用4.5元。
2.小兰的身高是1.5 m,她的影长是2.4 m。如果同一时间、同一地点测得一棵树的影子长4 m,这棵树有多高?
教材第61页“练习十一”第3题
解:设这棵树高x m。
答:这棵树高2.5 m。
3.中国空间站在太空中绕地球运行6周大约需要 9小时,运行15周大约要用多长时间?
解:设运行15周大约要用x小时。
答:运行15周大约要用22.5小时。
教材第61页“练习十一”第4题
中国太空站运行的速度是一定的。
4.一列由北京开往武汉的动车,从早晨7时出发,11时到达安阳。北京到安阳的铁路长大约是500 km。按照这样的平均速度,北京到武汉的铁路长大约是1200 km。从北京到武汉10小时能到吗?
解:设从北京到武汉需要x小时。
11时-7时=4时
答:从北京到武汉10小时能到。
有两条质地相同的绳子,长度相等,粗细不同。如果
从两条绳子一端点燃,细绳子40分钟可以燃尽,粗绳
子120分钟才能燃尽。如果从两条绳子的一端同时点燃,
经过一段时间后,又同时把它们熄灭。这时细绳子还剩
10厘米,粗绳子还剩30厘米,这两条绳子原来长多少
厘米?
10 cm
30 cm
拓展提升
10cm
30cm
解:设这两条绳子原来的长度是x厘米。
(x-10): =(x-30):
0
答:这两条绳子原来的长度是40厘米。
课堂小结
这节课你有什么收获?
用正比例解决问题的步骤
1
找出题目中相关联的两种量。
2
分析这两种量中相对应的两个数的比值是否一定,判断能否用比例解决。
3
设未知数,列正比例关系式。解方程,检验并作答。
4 比例
3.比例的应用
数学人教版六年级下册
第2课时 用比例解决问题(2)
学习目标
进一步理解反比例的意义,掌握用反比例知识解决问题的方法与步骤。
正确利用反比例知识列出方程,解决生活中简单的实际问题。
【重点】
利用反比例关系列出含有未知数的等式,运用反比例知识正确解决问题。
【难点】
掌握用反比例知识解答应用题的步骤和
方法。
课堂导入
解:设要花x分钟才能完成。
240∶2 = 600∶x
5
答:要花5分钟才能完成。
每分钟跳的数量一定。
宁宁2分钟跳绳240下,照这样计算,每天跳绳600下,要花多少分钟才能完成?
新知探究
某办公楼原来平均每天照明用电100千瓦时。改用节能灯以后,平均每天只用电25千瓦时。原来5天的用电量现在可以用多少天?
教材第60页例6
题目中涉及了哪些量?这些量成什么数量关系?
6
某办公楼原来平均每天照明用电100千瓦时。改用节能灯以后,平均每天只用电25千瓦时。原来5天的用电量现在可以用多少天?
原来 现在
每天的用电量
所求问题 100千瓦时
原来5天的用电量现在可以用多少天?
25千瓦时
教材第60页例6
6
原来 现在
每天的用电量
所求问题 100千瓦时
原来5天的用电量现在可以用多少天?
25千瓦时
教材第60页例6
每天的用电量×天数=用电总量
一定
成正比例关系
教材第60页例6
你能用什么方法解决问题?
原来 现在
每天的用电量
所求问题 100千瓦时
原来5天的用电量现在可以用多少天?
25千瓦时
教材第60页例6
可以先求出总用电量,再求现在的用电天数。
100×5=500(千瓦时)
答:原来5天的用电量现在可以用20天。
500÷25=20(天)
原来 现在
每天的用电量
所求问题 100千瓦时
原来5天的用电量现在可以用多少天?
25千瓦时
教材第60页例6
还可以用比例的方法解决。
当总的用电量一定时,用电时间与单位时间内的用电量成反比例关系。
也就是说,每天的用电量与用电天数的乘积相等。
原来 现在
每天的用电量
所求问题 100千瓦时
原来5天的用电量现在可以用多少天?
25千瓦时
教材第60页例6
解:设原来5天的用电量现在可以用x天。
25x = 100×5
x =
x = 20
答:原来5天的用电量现在可以用20天。
原来 现在
每天的用电量
所求问题 100千瓦时
原来5天的用电量现在可以用多少天?
25千瓦时
请你总结出解决本题的方法。
解决这个问题的关键是找到哪两个量的乘积一定。
1
只要两个量的乘积一定,就可以用反比例关系解答。
2
用正比例、反比例解决问题有什么相同点和不同点?
都有一个固定的量。
同
比值固定,用正比例解决问题
乘积固定,用反比例解决问题
异
现在30天的用电量原来只够用多少天?
解:设现在30天的用电量原来只够用y天。
答:现在30天的用电量原来只够用7.5天。
.5
问题延伸
y =
1.小商店有两种圆珠笔。小明带的钱刚好可以买4支单价是1.5元的圆珠笔,如果他只买单价是2元的圆珠笔,可以买多少支?
总钱数不变。
课堂练习
教材第60页“做一做”第2题
4支×1.5元 = 购买圆珠笔的数量×2元
教材第60页“做一做”第2题
解:设可以买x支。
答:可以买3支。
1.小商店有两种圆珠笔。小明带的钱刚好可以买4支单价是1.5元的圆珠笔,如果他只买单价是2元的圆珠笔,可以买多少支?
2.工程队修一条水渠,每天工作6小时,12天可
以完成。如果每小时的工作量不变,每天工作
8小时,多少天可以完成任务?
教材第62页“练习十一”第5题
工作总量一定。
解:设x天可以完成任务。
答:9天可以完成任务。
3.小林读一本文学名著,如果每天读30页,8天
可以读完。小林想6天读完,那么平均每天要
读多少页?
解:设平均每天读x页。
答:平均每天要读40页。
这本书的总页数一定。
教材第62页“练习十一”第8题
4.用方砖铺地,如果用面积为0.16m2的砖,需
要1200块。若改用边长为0.5m的砖,需要多
少块?(用比例解决)
解:设需要x块砖。
0.16×1200 = 0.5×0.5×x
答:需要768块砖。
铺的总面积一定。
拓展提升
1.一艘轮船从甲港开往乙港,去时顺水,每小时行24
千米,15小时到达;返回时逆水,速度降低了25%,
返回时用了多少小时?(用比例解)
返回时的速度:24×(1-25%)
往返路程一定。
1.一艘轮船从甲港开往乙港,去时顺水,每小时行24
千米,15小时到达;返回时逆水,速度降低了25%,
返回时用了多少小时?(用比例解)
解:设返回时用了x小时。
24×(1-25%)x = 24×15
24×0.75x = 24×15
0.75x = 15
x = 20
答:返回时用了20小时。
2.铺设一条煤气管道,计划每天铺设120 m,用20天
完成任务。因居民着急使用,上级领导要求每天多
铺设25%,这样可以提前几天完成任务?(用比
例解答)
现在每天铺设的长度:120×(1+25%)
解:设现在需要x天完成。
120×20 = 120×(1+25%)x
150x = 2400
x = 16
20-16 = 4(天)
答:这样可以提前4天完成任务。
课堂小结
这节课你有什么收获?
用反比例解决问题的步骤
1
找出题目中相关联的两种量。
2
分析这两种量中相对应的两个数的乘积是否一定,判断能否用比例解决。
3
设未知数,列反比例关系式。解方程,检验并作答。
Thank you!
4 比例
3.比例的应用
数学人教版六年级下册
第1课时 用比例解决问题(1)
进一步理解正比例的意义,掌握用正比例知识解决问题的方法与步骤。
正确利用正比例知识列出方程,解决生活中简单的实际问题。
学习目标
【重点】
利用正比例关系列出含有未知数的等式,运用正比例知识正确解决问题。
【难点】
掌握用正比例知识解答应用题的步骤和
方法。
课堂导入
判断下列每题中的两种量是否成比例关系,成什么比例关系?
(1)已知A÷B=C。
当A一定时,B和C成( )比例关系。
当B一定时,A和C成( )比例关系。
当C一定时,A和B成( )比例关系。
反
正
正
(2)购买文具的单价一定时,总价和数量的
关系。
总价÷数量=单价
成正比例关系
判断下列每题中的两种量是否成比例关系,成什么比例关系?
一定
用水量
水费
用水量
新知探究
张阿姨家上个月用了8 t水,水费是40元。李奶奶家上个月用了10 t水,李奶奶家上个月的水费是多少?
教材第59页例5
你能从题中获取哪些信息?
5
用户 上个月用水量 水费
张阿姨家
李奶奶家
8 t
40元
10 t
?元
张阿姨家上个月用了8 t水,水费是40元。李奶奶家上个月用了10 t水,李奶奶家上个月的水费是多少?
教材第59页例5
5
张阿姨家上个月用了8 t水,水费是40元。李奶奶家上个月用了10 t水,李奶奶家上个月的水费是多少?
教材第59页例5
5
这些量成什么数量关系?
水费÷用水量=水的单价
一定
成正比例关系
教材第59页例5
方法一:我先算出每吨水的价钱,再算10 t水多少钱。
答:李奶奶家上个月的水费是。
=
教材第59页例5
方法二:还可以用比例的方法解决。
每吨水的价钱一定,所以水费和用水吨数成正比例关系。
两家的水费和用水吨数的比值相等。
教材第59页例5
解:设李奶奶家上个月的水费是x元。
=
8x = 40×10
x = 50
x =
=
还可以这样列式:
=
8x = 40×10
x = 50
请你总结出解决本题的方法。
解这个问题的关键是找到不变的量。
1
只要两个量的比值一定,就可以用正比例关系解答。
2
虽然未知量变了,但题中水费和用水的吨数的正比例关系没变。
问题延伸
王爷爷家上个月的水费是60元,他家上个月用了多少吨水?
问题延伸
王爷爷家上个月的水费是60元,他家上个月用了多少吨水?
解:设他家上个月用了x吨水。
答:他家上个月用了12吨水。
课堂练习
1.小明买4支圆珠笔用了6元。小刚想买3支同样
的圆珠笔,要用多少钱?
教材第60页“做一做”第1题
圆珠笔的单价不变。
解:设买3支同样的圆珠笔,要用x元。
答:买3支同样的圆珠笔,要用4.5元。
2.小兰的身高是1.5 m,她的影长是2.4 m。如果同一时间、同一地点测得一棵树的影子长4 m,这棵树有多高?
教材第61页“练习十一”第3题
解:设这棵树高x m。
答:这棵树高2.5 m。
3.中国空间站在太空中绕地球运行6周大约需要 9小时,运行15周大约要用多长时间?
解:设运行15周大约要用x小时。
答:运行15周大约要用22.5小时。
教材第61页“练习十一”第4题
中国太空站运行的速度是一定的。
4.一列由北京开往武汉的动车,从早晨7时出发,11时到达安阳。北京到安阳的铁路长大约是500 km。按照这样的平均速度,北京到武汉的铁路长大约是1200 km。从北京到武汉10小时能到吗?
解:设从北京到武汉需要x小时。
11时-7时=4时
答:从北京到武汉10小时能到。
有两条质地相同的绳子,长度相等,粗细不同。如果
从两条绳子一端点燃,细绳子40分钟可以燃尽,粗绳
子120分钟才能燃尽。如果从两条绳子的一端同时点燃,
经过一段时间后,又同时把它们熄灭。这时细绳子还剩
10厘米,粗绳子还剩30厘米,这两条绳子原来长多少
厘米?
10 cm
30 cm
拓展提升
10cm
30cm
解:设这两条绳子原来的长度是x厘米。
(x-10): =(x-30):
0
答:这两条绳子原来的长度是40厘米。
课堂小结
这节课你有什么收获?
用正比例解决问题的步骤
1
找出题目中相关联的两种量。
2
分析这两种量中相对应的两个数的比值是否一定,判断能否用比例解决。
3
设未知数,列正比例关系式。解方程,检验并作答。
4 比例
3.比例的应用
数学人教版六年级下册
第2课时 用比例解决问题(2)
学习目标
进一步理解反比例的意义,掌握用反比例知识解决问题的方法与步骤。
正确利用反比例知识列出方程,解决生活中简单的实际问题。
【重点】
利用反比例关系列出含有未知数的等式,运用反比例知识正确解决问题。
【难点】
掌握用反比例知识解答应用题的步骤和
方法。
课堂导入
解:设要花x分钟才能完成。
240∶2 = 600∶x
5
答:要花5分钟才能完成。
每分钟跳的数量一定。
宁宁2分钟跳绳240下,照这样计算,每天跳绳600下,要花多少分钟才能完成?
新知探究
某办公楼原来平均每天照明用电100千瓦时。改用节能灯以后,平均每天只用电25千瓦时。原来5天的用电量现在可以用多少天?
教材第60页例6
题目中涉及了哪些量?这些量成什么数量关系?
6
某办公楼原来平均每天照明用电100千瓦时。改用节能灯以后,平均每天只用电25千瓦时。原来5天的用电量现在可以用多少天?
原来 现在
每天的用电量
所求问题 100千瓦时
原来5天的用电量现在可以用多少天?
25千瓦时
教材第60页例6
6
原来 现在
每天的用电量
所求问题 100千瓦时
原来5天的用电量现在可以用多少天?
25千瓦时
教材第60页例6
每天的用电量×天数=用电总量
一定
成正比例关系
教材第60页例6
你能用什么方法解决问题?
原来 现在
每天的用电量
所求问题 100千瓦时
原来5天的用电量现在可以用多少天?
25千瓦时
教材第60页例6
可以先求出总用电量,再求现在的用电天数。
100×5=500(千瓦时)
答:原来5天的用电量现在可以用20天。
500÷25=20(天)
原来 现在
每天的用电量
所求问题 100千瓦时
原来5天的用电量现在可以用多少天?
25千瓦时
教材第60页例6
还可以用比例的方法解决。
当总的用电量一定时,用电时间与单位时间内的用电量成反比例关系。
也就是说,每天的用电量与用电天数的乘积相等。
原来 现在
每天的用电量
所求问题 100千瓦时
原来5天的用电量现在可以用多少天?
25千瓦时
教材第60页例6
解:设原来5天的用电量现在可以用x天。
25x = 100×5
x =
x = 20
答:原来5天的用电量现在可以用20天。
原来 现在
每天的用电量
所求问题 100千瓦时
原来5天的用电量现在可以用多少天?
25千瓦时
请你总结出解决本题的方法。
解决这个问题的关键是找到哪两个量的乘积一定。
1
只要两个量的乘积一定,就可以用反比例关系解答。
2
用正比例、反比例解决问题有什么相同点和不同点?
都有一个固定的量。
同
比值固定,用正比例解决问题
乘积固定,用反比例解决问题
异
现在30天的用电量原来只够用多少天?
解:设现在30天的用电量原来只够用y天。
答:现在30天的用电量原来只够用7.5天。
.5
问题延伸
y =
1.小商店有两种圆珠笔。小明带的钱刚好可以买4支单价是1.5元的圆珠笔,如果他只买单价是2元的圆珠笔,可以买多少支?
总钱数不变。
课堂练习
教材第60页“做一做”第2题
4支×1.5元 = 购买圆珠笔的数量×2元
教材第60页“做一做”第2题
解:设可以买x支。
答:可以买3支。
1.小商店有两种圆珠笔。小明带的钱刚好可以买4支单价是1.5元的圆珠笔,如果他只买单价是2元的圆珠笔,可以买多少支?
2.工程队修一条水渠,每天工作6小时,12天可
以完成。如果每小时的工作量不变,每天工作
8小时,多少天可以完成任务?
教材第62页“练习十一”第5题
工作总量一定。
解:设x天可以完成任务。
答:9天可以完成任务。
3.小林读一本文学名著,如果每天读30页,8天
可以读完。小林想6天读完,那么平均每天要
读多少页?
解:设平均每天读x页。
答:平均每天要读40页。
这本书的总页数一定。
教材第62页“练习十一”第8题
4.用方砖铺地,如果用面积为0.16m2的砖,需
要1200块。若改用边长为0.5m的砖,需要多
少块?(用比例解决)
解:设需要x块砖。
0.16×1200 = 0.5×0.5×x
答:需要768块砖。
铺的总面积一定。
拓展提升
1.一艘轮船从甲港开往乙港,去时顺水,每小时行24
千米,15小时到达;返回时逆水,速度降低了25%,
返回时用了多少小时?(用比例解)
返回时的速度:24×(1-25%)
往返路程一定。
1.一艘轮船从甲港开往乙港,去时顺水,每小时行24
千米,15小时到达;返回时逆水,速度降低了25%,
返回时用了多少小时?(用比例解)
解:设返回时用了x小时。
24×(1-25%)x = 24×15
24×0.75x = 24×15
0.75x = 15
x = 20
答:返回时用了20小时。
2.铺设一条煤气管道,计划每天铺设120 m,用20天
完成任务。因居民着急使用,上级领导要求每天多
铺设25%,这样可以提前几天完成任务?(用比
例解答)
现在每天铺设的长度:120×(1+25%)
解:设现在需要x天完成。
120×20 = 120×(1+25%)x
150x = 2400
x = 16
20-16 = 4(天)
答:这样可以提前4天完成任务。
课堂小结
这节课你有什么收获?
用反比例解决问题的步骤
1
找出题目中相关联的两种量。
2
分析这两种量中相对应的两个数的乘积是否一定,判断能否用比例解决。
3
设未知数,列反比例关系式。解方程,检验并作答。
Thank you!
