比例的应用(课件)-六年级下册数学人教版(共78张PPT)
文档属性
| 名称 | 比例的应用(课件)-六年级下册数学人教版(共78张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-05 00:00:00 | ||
图片预览







文档简介
(共78张PPT)
4 比例
3.比例的应用
数学人教版六年级下册
第1课时 比例尺(1)
1. 结合生活实际认识比例尺,理解比例尺的意义,
能正确说明比例尺所表示的具体含义。
2. 认识数值比例尺和线段比例尺,能将线段比例尺
改成数值比例尺,将数值比例尺改成线段比例尺。
学习目标
【重点】认识比例尺的具体含义。
【难点】线段比例尺与数值比例尺的互化。
课堂导入
下图是一个房屋设计图,你知道工人是怎样根据图纸完成建筑的吗?
新知探究
在绘制地图和平面图的时候,有时需要把实际距离按一定的比缩小(或放大),再画在图纸上。这时,就要确定图上距离和相对应的实际距离的比。
一幅图的图上距离和实际距离的比,叫作这幅图的比例尺。
或
图上距离∶实际距离=比例尺
比例尺:1∶400
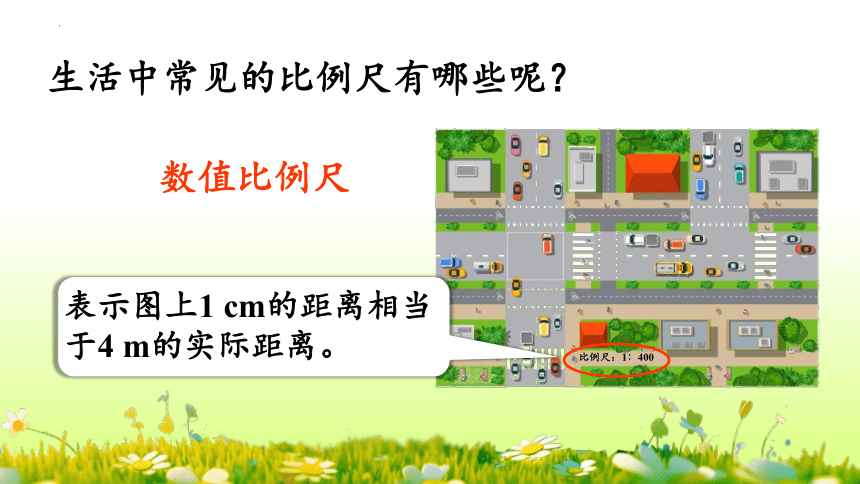
生活中常见的比例尺有哪些呢?
数值比例尺
表示图上1 cm的距离相当于4 m的实际距离。
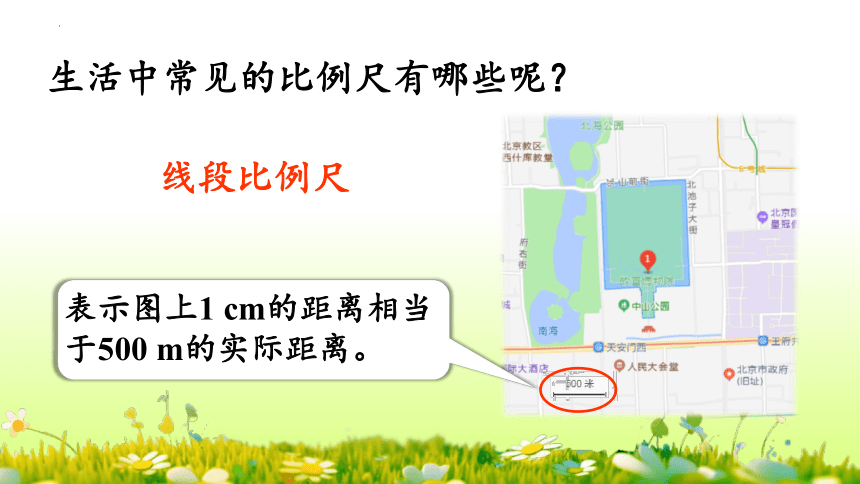
生活中常见的比例尺有哪些呢?
线段比例尺
表示图上1 cm的距离相当于500 m的实际距离。
生活中常见的比例尺有哪些呢?
缩小比例尺
在绘图时,有时需要把实际距离按一定的比缩小后画在图纸上,用这个方法得到的比例尺就是缩小比例尺。如:1∶1000000。
生活中常见的比例尺有哪些呢?
放大比例尺
在绘制比较精细的零件图时,经常需要把零件的尺寸按一定的比放大,用这种方法得到的比例尺就是放大比例尺。如:2∶1。
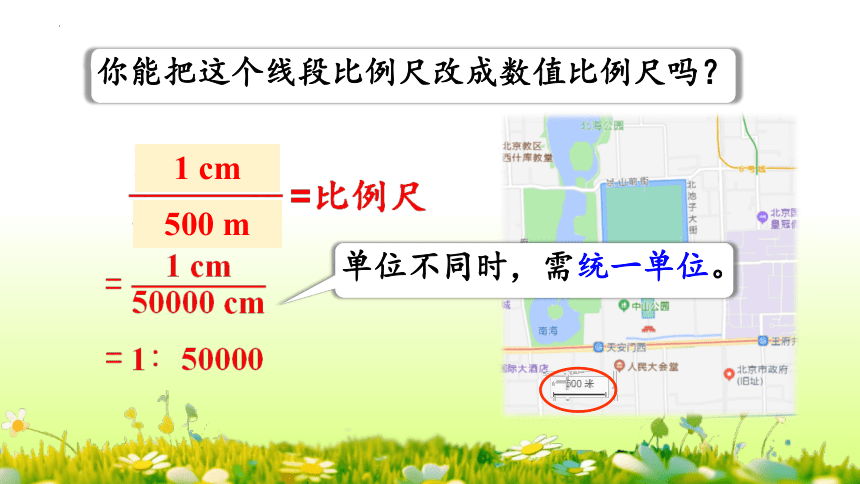
你能把这个线段比例尺改成数值比例尺吗?
1 cm
500 m
=
= 1∶
=
单位不同时,需统一单位。
1 cm
500 m
=
= 1∶
=
思考:这个比例尺表示图上距离是实际距离的
实际距离是图上距离的
,
倍。
几分之几?
多少倍?
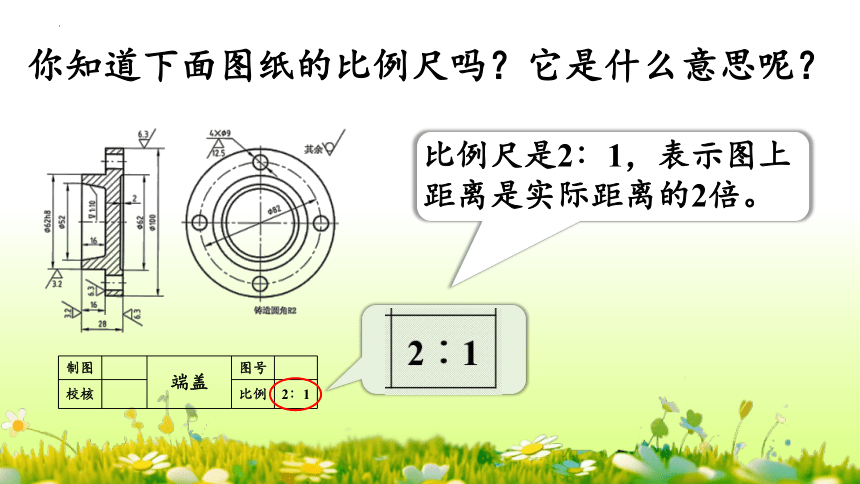
制图 端盖 图号
校核 比例 2∶1
你知道下面图纸的比例尺吗?它是什么意思呢?
2∶1
比例尺是2∶1,表示图上距离是实际距离的2倍。
制图 端盖 图号
校核 比例 2∶1
在绘制比较精细的零件图时,经常需要把零件的尺寸按一定的比放大。
你知道下面图纸的比例尺吗?它是什么意思呢?
观察这些比例尺,你发现了什么?
制图 端盖 图号
校核 比例 2∶1
1∶50000
2∶1
为了计算方便,一般把比例尺写成
前项或后项是1的形式。
两地之间的实际距离是120 km,在一幅地图上量得两地的图上距离是2.4 cm。这幅地图的比例尺是多少?
2.4 cm
120 km
= 1∶
答:这幅地图的比例尺是1∶5000000。
教材第52页例1
1
1.填空题。
(1)一幅图的图上距离和实际距离的比,叫做这幅图
的( )。
(2) 这个比例尺是( )比例尺,
表示图上1 cm相当于实际距离( ),将这个比
例尺改写成数字比例尺是( )。
(3)20∶1这个比例尺表示图上距离( )cm相当于
实际距离1 cm。
0
50
100 km
比例尺
线段
50 km
1∶5000000
20
课堂练习
(2)在一幅地图上,用1 cm的图上距离表示6 km的实
际距离,这幅地图的比例尺是 ( )
(1)比例尺是1∶5,这张图的图上距离是实际距离的
5倍。 ( )
(3)一幅图的比例尺是1∶300 ( )
×
×
2.判断题。
要注意比例尺的单位。
比例尺表示倍比关系,不能带单位。
教学楼
实验室
操场
花坛
大门
北
教学楼
实验室
操场
花坛
大门
北
3.校园里有哪些建筑?分别在哪些方位?
形状、大小分明
形状、大小都一样
√
哪幅图画的更好?为什么?
4.说说下面的比例尺分别代表什么?
表示图上1 cm的距离相当于40千米的实际距离。
表示图上1 cm的距离相当于80千米的实际距离。
5.一个圆柱形零件的高是 ,在图纸上的高是 。
这幅图纸的比例尺是多少?
∶
2 cm = 20 mm
20∶5 = 4∶1
答:这幅图纸的比例尺是4∶1。
教材第52页上面“做一做”
图上距离
实际距离
=比例尺
5 mm
2 cm
6.一幅地图的比例尺是1∶30000000,你能用线段比例
尺表示出来吗?
教材第54页“练习十”第1题
30000000 cm = 300 km
0
300 km
线段比例尺:
先转化为统一单位。
地图上1厘米相当于实际距离300千米。
(1)量一量团结路在图上的长度,求出这幅图
的比例尺。
7.团结路的实际长度是1800 m。
1800 m=180000 cm
6∶180000
答:这幅图的比例尺是
1∶30000。
=1∶30000
教材第54页“练习十”第3题
北
图上距离是6 cm。
(2)将这幅图的比例尺用线段比例尺表示出来。
0
300 m
30000 cm = 300 m
线段比例尺:
7.团结路的实际长度是1800 m。
北
图上距离是6 cm。
教材第54页“练习十”第3题
拓展提升
1.文星大道的实际距离是12 km。
文星大道
江碧路
体育场
湖泊
南浦路
医院
商场
12 km=1200000 cm
4∶1200000=1∶300000
答:这幅图的比例尺是1∶300000。
(1)量一量文星大道在图上的距离,求出这幅图的比
例尺。
图上距离4 cm。
1.文星大道的实际距离是12 km。
文星大道
江碧路
体育场
湖泊
南浦路
医院
商场
300000 cm=3 km
(2)将这幅图的比例尺用线段比例尺表示出来。
图上距离4 cm。
线段比例尺是:
3
6
9
km
0
( )
( )
( )
课堂小结
这节课你有什么收获?
比例尺
数值比例尺
1∶50000
线段比例尺
放大比例尺
缩小比例尺
2∶1
1∶500000
0
50 km
计算时要注意统一单位。
为了计算方便,通常把比例尺写成前项或后项是1的形式。
按表现形式分
按将实际距离放大或缩小分
4 比例
3.比例的应用
数学人教版六年级下册
第2课时 比例尺(2)
1. 进一步理解比例尺的意义,掌握比例尺、图上距离和实际距离的计算方法。
2. 综合运用比例尺解决实际问题。
3. 体会比例尺的价值,体会数学与生活的密切联系。
学习目标
【重点】掌握比例尺、图上距离和实际距离的计算方法。
【难点】综合运用比例尺解决实际问题。
我可以用5秒钟从北京爬到上海。
课堂导入
脑筋急转弯。
它是怎么做到的?
我可以用5秒钟从北京爬到上海。
脑筋急转弯。
它是在地图上爬的!
要想知道两地之间的实际距离是多少,需要知道哪些条件?
?
√
√
新知探究
比例尺
图上距离
在一幅比例尺为1∶30000的地图上,北京地铁2号线的长度大约是77 cm。北京地铁2号线的实际长度大约是多少千米?
已知条件
所求问题
你得到了哪些数学信息?
图上距离大约是77 cm,
比例尺是1∶30000。
实际长度大约是多少千米?
?
怎样解决呢?
教材第52页例2
教材第52页例2
77
方法一:
比例尺
图上距离
在一幅比例尺为1∶30000的地图上,北京地铁2号线的长度大约是77 cm。北京地铁2号线的实际长度大约是多少千米?
?
1∶30000
77
方法一:
1∶30000
教材第52页例2
计算时,要注意单位。
实际距离= 77×30000÷1
= 2310000
2310000 cm = 23.1 km
答:北京地铁2号线的实际长度大约是23.1 km。
解:设北京地铁2号线的实际长度大约是x cm。
77
方法二:
可以用解比例的方法求出实际距离。
2310000 cm = 23.1 km
x
1∶30000
实际距离
77
1∶30000
方法三:
2310000 cm = 23.1 km
观察三种方法,它们的依据是什么?有什么共同点?
实际距离
方法三:
方法二:
方法一:
比例的基本性质
依据:
课堂练习
教材第52页“做一做”
1.先把右图中的线段比例尺改写成数值比例尺,再用直尺量出图中河西村与汽车站之间的距离,并计算出两地的实际距离大约是多少。
600 m = 60000 cm
数值比例尺:1∶60000
3 cm
图上距离:3 cm
教材第52页“做一做”
比例尺:1∶60000
3
1∶60000
1.先把右图中的线段比例尺改写成数值比例尺,再用直尺量出图中河西村与汽车站之间的距离,并计算出两地的实际距离大约是多少。
3 cm
方法一:
解:设两地的实际距离大约是 x cm。
3
1∶60000
x
计算时,要注意单位。
答:两地的实际距离大约是1.8 km。
实际距离
3
方法二:
答:两地的实际距离大约是1.8 km。
2.在比例尺是1∶的地图上,量得武汉到北京的距
离是14.4厘米,北京到武汉的实际距离大约是多少千米?
解:设北京到武汉的实际距离是 x cm 。
14.4
1∶8000000
x
0
3.在一幅中国地图上,选取两个城市。量出它们在图上
的距离,再根据比例尺算出它们的实际距离。
教材第55页第6题
1∶18000000
武汉
杭州
3.1
解:设武汉至杭州的实际距离约为 x cm 。
x
0
答:武汉至杭州的实际距离约为558 km。
3.1 cm
拓展提升
1.在比例尺为1∶2000000的地图上,量得甲地到乙地的距
离是16 cm。如果一辆汽车以每小时50公里的速度从甲地
开往乙地,6小时能到达吗?
先算出甲、乙两地的实际距离,再根据“距离÷速度=时间”来计算所用的时间,最后与6小时进行比较。
1.在比例尺为1∶2000000的地图上,量得甲地到乙地的距
离是16 cm。如果一辆汽车以每小时50公里的速度从甲地
开往乙地,6小时能到达吗?
答:6小时不能到达。
>6
解:设甲、乙两地的实际距离为 x cm 。
16
x
2.如下图,量得宜城至铜陵的高速路距离为12 cm,上午
8:00从宜城出发,什么时候到达铜陵?(车辆平均时速
为100 km/h)
解:设宜城到铜陵的实际距离为x cm 。
1∶6000000
12 cm
12
x
1∶6000000
12 cm
12分
答:15时12分到达铜陵。
2.如下图,量得宜城至铜陵的高速路距离为12 cm,上午
8:00从宜城出发,什么时候到达铜陵?(车辆平均时速
为100 km/h)
6∶1是放大比例尺。
3.在一张比例尺为6∶1精密零件的图纸上,量得零件的
长为24 mm,这个零件的实际长度是多少?
24
6∶1
解:设这个零件的实际长度是 x mm 。
x
答:这个零件的实际长度是4 mm。
课堂小结
这节课你有什么收获?
求实际距离的方法
方程法
1
可知=
算术法
2
1.设未知数x。
根据
2.列比例。
3.解比例。
用除法计算。
转化为求图上距离的几倍是多少来计算。
3
4 比例
3.比例的应用
数学人教版六年级下册
第3课时 比例尺(3)
1.能根据比例尺及相应的条件画出平面图。
2.培养联系实际解决问题的能力,感受数学在生活中的广泛应用。
学习目标
【重点】把比例尺应用到实际生活中,解决实 际问题。
【难点】根据比例尺及相应的条件画平面图。
课堂导入
我想在长4 m,宽3 m,高3 m的书房北面放置一个长2 m,宽1.5 m,高2 m的书架,南面放置一个长1.5 m,宽1 m,高0.8 m的书桌。
你能帮她画出书房的平面设计图吗?
3 m
0.8 m
4 m
3 m
2 m
2 m
1.5 m
1.5 m
1 m
上面哪幅平面设计图设计得更标准?
4 m
3 m
北
书架
书桌
4 m
3 m
北
书架
书桌
√
画出的书架、书桌形状与要求一致。
新知探究
小明家在学校正西方向,距学校200 m;小亮家在小明家正东方向,距小明家400 m;小红家在学校正北方向,距学校250 m。在下图中画出他们三家和学校的位置平面图(比例尺1∶10000)。
教材第53页例3
北
学校
0
( ) m
3
观察题目,说说已知什么 求什么?
还已知比例尺是1∶10000,求的是
他们三家到学校的图上距离。
已知小明家在学校正西方向,距学校200 m;小亮家在小明家正东方向,距小明家400 m;小红家在学校正北方向,距学校250 m。
图上距离
先求图上距离
计算图上距离之前,记得要先把实际距离化成用“cm”作单位的数。
200 m=20000 cm
400 m=40000 cm
250 m=25000 cm
由长度单位间的换算方法可知100 m = 10000 cm。
单位换算
小明家到学校的图上距离:
小红家到学校的图上距离:
小亮家到学校的图上距离:
25000× = 2.5(cm)
(40000 - 20000)× = 2(cm)
20000× = 2(cm)
求图上距离
( ) m
100
小明家
北
学校
0
再画出平面图
小亮家
小明家
学校
( ) m
100
0
北
再画出平面图
小红家
小明家
学校
( ) m
100
0
北
再画出平面图
小亮家
应用比例尺画平面图时,要先根据比例尺和实际距离求出图上距离,再根据距离和方向画出相应的位置,并标明比例尺。
课堂练习
1.学校要建一个长80 m、宽60 m的长方形操场。请在右图中画出操场的平面图(比例尺 1∶2000)。
教材第53页“做一做”
先要算出长和宽
的图上距离。
0
20 m
2000 cm=20 m
80 m=8000 cm
60 m=6000 cm
操场平面图
0
20 m
4 cm
3 cm
1.学校要建一个长80 m、宽60 m的长方形操场。请在右图中画出操场的平面图(比例尺 1∶2000)。
2.两个城市之间的铁路线大约长1900 km。在一幅比例尺为1 : 40000000的地图上,这两个城市之间铁路线的长度大约是多少厘米?
教材第55页“练习十”第7题
1900 km=190000000 cm
答:这两个城市之间铁路线的长度大约是4.75 cm。
3.填表。
教材第55页“练习十”第8题
比例尺 图上距离 实际距离
1∶50000 1.8 km
1∶2000000 450 km
1∶60000000 15 cm
3.6 cm
22.5 cm
9000 km
= 3.6(cm)
= 22.5(cm)
= 900000000(cm) = 9000(km)
先根据图上距离列式。
再根据实际距离=图上距离÷比例尺列式。
4.小明家的正西面100米是商场,商场的正北
面500米是学校,学校的正西面300米是小
红家,小红家的正南面200米是医院。请你
确定比例尺后画出平面图。
北
比例尺1∶20000
小明家
确定比例尺时要考虑哪些数据?
商场
100 m=10000 cm
4.小明家的正西面100米是商场,商场的正北
面500米是学校,学校的正西面300米是小
红家,小红家的正南面200米是医院。请你
确定比例尺后画出平面图。
北
小明家
比例尺1∶20000
4.小明家的正西面100米是商场,商场的正北
面500米是学校,学校的正西面300米是小
红家,小红家的正南面200米是医院。请你
确定比例尺后画出平面图。
学校
商场
500 m=50000 cm
北
比例尺1∶20000
小明家
4.小明家的正西面100米是商场,商场的正北
面500米是学校,学校的正西面300米是小
红家,小红家的正南面200米是医院。请你
确定比例尺后画出平面图。
300 m=30000 cm
小红家
北
比例尺1∶20000
小明家
商场
学校
医院
4.小明家的正西面100米是商场,商场的正北
面500米是学校,学校的正西面300米是小
红家,小红家的正南面200米是医院。请你
确定比例尺后画出平面图。
200 m=20000 cm
北
比例尺1∶20000
小明家
商场
学校
小红家
拓展提升
1.在比例尺为1 ∶ 400000的地图上,甲、乙两地
相距12 cm,现在要画一幅比例尺为1:500000
的地图,甲、乙两地的图上距离是多少厘米?
不论用哪个比例尺,相同两个地方之间的实际距离是不变的。
可以先求出两地之间的实际距离,
再求两地之间的图上距离。
甲、乙两地在比例尺为1∶500000的地图上的距离:
甲、乙两地的实际距离:
12 =4800000(cm)
答:甲、乙两地的图上距离是9.6 cm。
1.在比例尺为1 ∶ 400000的地图上,甲、乙两地
相距12 cm,现在要画一幅比例尺为1:500000
的地图,甲、乙两地的图上距离是多少厘米?
2.量得一个操场的长是800 m,宽是600 m,将其
画在比例尺为1∶40000的图纸上,这个操场的
面积是多少平方厘米?
要想知道这个操场在图纸上的面积,就要先求出这个操场在图纸上的长和宽。
800 m = 80000 cm
600 m = 60000 cm
2.量得一个操场的长是800 m,宽是600 m,将其
画在比例尺为1∶40000的图纸上,这个操场的
面积是多少平方厘米?
操场的图上长度:
80000× = 2(cm)
操场的图上宽度:
60000×= 1.5(cm)
操场的图上面积:
2×1.5 = 3()
答:在图纸上,这个操场的面积是3。
应用比例尺画平面图的步骤
课堂小结
这节课你有什么收获?
3
1
2
根据实际距离与比例尺求出图上距离。
根据图上距离和方向画出相应的平面图,并标明平面图的名称及比例尺。
根据实际距离与纸张的大小确定平面图的比例尺。
Thank you!
4 比例
3.比例的应用
数学人教版六年级下册
第1课时 比例尺(1)
1. 结合生活实际认识比例尺,理解比例尺的意义,
能正确说明比例尺所表示的具体含义。
2. 认识数值比例尺和线段比例尺,能将线段比例尺
改成数值比例尺,将数值比例尺改成线段比例尺。
学习目标
【重点】认识比例尺的具体含义。
【难点】线段比例尺与数值比例尺的互化。
课堂导入
下图是一个房屋设计图,你知道工人是怎样根据图纸完成建筑的吗?
新知探究
在绘制地图和平面图的时候,有时需要把实际距离按一定的比缩小(或放大),再画在图纸上。这时,就要确定图上距离和相对应的实际距离的比。
一幅图的图上距离和实际距离的比,叫作这幅图的比例尺。
或
图上距离∶实际距离=比例尺
比例尺:1∶400
生活中常见的比例尺有哪些呢?
数值比例尺
表示图上1 cm的距离相当于4 m的实际距离。
生活中常见的比例尺有哪些呢?
线段比例尺
表示图上1 cm的距离相当于500 m的实际距离。
生活中常见的比例尺有哪些呢?
缩小比例尺
在绘图时,有时需要把实际距离按一定的比缩小后画在图纸上,用这个方法得到的比例尺就是缩小比例尺。如:1∶1000000。
生活中常见的比例尺有哪些呢?
放大比例尺
在绘制比较精细的零件图时,经常需要把零件的尺寸按一定的比放大,用这种方法得到的比例尺就是放大比例尺。如:2∶1。
你能把这个线段比例尺改成数值比例尺吗?
1 cm
500 m
=
= 1∶
=
单位不同时,需统一单位。
1 cm
500 m
=
= 1∶
=
思考:这个比例尺表示图上距离是实际距离的
实际距离是图上距离的
,
倍。
几分之几?
多少倍?
制图 端盖 图号
校核 比例 2∶1
你知道下面图纸的比例尺吗?它是什么意思呢?
2∶1
比例尺是2∶1,表示图上距离是实际距离的2倍。
制图 端盖 图号
校核 比例 2∶1
在绘制比较精细的零件图时,经常需要把零件的尺寸按一定的比放大。
你知道下面图纸的比例尺吗?它是什么意思呢?
观察这些比例尺,你发现了什么?
制图 端盖 图号
校核 比例 2∶1
1∶50000
2∶1
为了计算方便,一般把比例尺写成
前项或后项是1的形式。
两地之间的实际距离是120 km,在一幅地图上量得两地的图上距离是2.4 cm。这幅地图的比例尺是多少?
2.4 cm
120 km
= 1∶
答:这幅地图的比例尺是1∶5000000。
教材第52页例1
1
1.填空题。
(1)一幅图的图上距离和实际距离的比,叫做这幅图
的( )。
(2) 这个比例尺是( )比例尺,
表示图上1 cm相当于实际距离( ),将这个比
例尺改写成数字比例尺是( )。
(3)20∶1这个比例尺表示图上距离( )cm相当于
实际距离1 cm。
0
50
100 km
比例尺
线段
50 km
1∶5000000
20
课堂练习
(2)在一幅地图上,用1 cm的图上距离表示6 km的实
际距离,这幅地图的比例尺是 ( )
(1)比例尺是1∶5,这张图的图上距离是实际距离的
5倍。 ( )
(3)一幅图的比例尺是1∶300 ( )
×
×
2.判断题。
要注意比例尺的单位。
比例尺表示倍比关系,不能带单位。
教学楼
实验室
操场
花坛
大门
北
教学楼
实验室
操场
花坛
大门
北
3.校园里有哪些建筑?分别在哪些方位?
形状、大小分明
形状、大小都一样
√
哪幅图画的更好?为什么?
4.说说下面的比例尺分别代表什么?
表示图上1 cm的距离相当于40千米的实际距离。
表示图上1 cm的距离相当于80千米的实际距离。
5.一个圆柱形零件的高是 ,在图纸上的高是 。
这幅图纸的比例尺是多少?
∶
2 cm = 20 mm
20∶5 = 4∶1
答:这幅图纸的比例尺是4∶1。
教材第52页上面“做一做”
图上距离
实际距离
=比例尺
5 mm
2 cm
6.一幅地图的比例尺是1∶30000000,你能用线段比例
尺表示出来吗?
教材第54页“练习十”第1题
30000000 cm = 300 km
0
300 km
线段比例尺:
先转化为统一单位。
地图上1厘米相当于实际距离300千米。
(1)量一量团结路在图上的长度,求出这幅图
的比例尺。
7.团结路的实际长度是1800 m。
1800 m=180000 cm
6∶180000
答:这幅图的比例尺是
1∶30000。
=1∶30000
教材第54页“练习十”第3题
北
图上距离是6 cm。
(2)将这幅图的比例尺用线段比例尺表示出来。
0
300 m
30000 cm = 300 m
线段比例尺:
7.团结路的实际长度是1800 m。
北
图上距离是6 cm。
教材第54页“练习十”第3题
拓展提升
1.文星大道的实际距离是12 km。
文星大道
江碧路
体育场
湖泊
南浦路
医院
商场
12 km=1200000 cm
4∶1200000=1∶300000
答:这幅图的比例尺是1∶300000。
(1)量一量文星大道在图上的距离,求出这幅图的比
例尺。
图上距离4 cm。
1.文星大道的实际距离是12 km。
文星大道
江碧路
体育场
湖泊
南浦路
医院
商场
300000 cm=3 km
(2)将这幅图的比例尺用线段比例尺表示出来。
图上距离4 cm。
线段比例尺是:
3
6
9
km
0
( )
( )
( )
课堂小结
这节课你有什么收获?
比例尺
数值比例尺
1∶50000
线段比例尺
放大比例尺
缩小比例尺
2∶1
1∶500000
0
50 km
计算时要注意统一单位。
为了计算方便,通常把比例尺写成前项或后项是1的形式。
按表现形式分
按将实际距离放大或缩小分
4 比例
3.比例的应用
数学人教版六年级下册
第2课时 比例尺(2)
1. 进一步理解比例尺的意义,掌握比例尺、图上距离和实际距离的计算方法。
2. 综合运用比例尺解决实际问题。
3. 体会比例尺的价值,体会数学与生活的密切联系。
学习目标
【重点】掌握比例尺、图上距离和实际距离的计算方法。
【难点】综合运用比例尺解决实际问题。
我可以用5秒钟从北京爬到上海。
课堂导入
脑筋急转弯。
它是怎么做到的?
我可以用5秒钟从北京爬到上海。
脑筋急转弯。
它是在地图上爬的!
要想知道两地之间的实际距离是多少,需要知道哪些条件?
?
√
√
新知探究
比例尺
图上距离
在一幅比例尺为1∶30000的地图上,北京地铁2号线的长度大约是77 cm。北京地铁2号线的实际长度大约是多少千米?
已知条件
所求问题
你得到了哪些数学信息?
图上距离大约是77 cm,
比例尺是1∶30000。
实际长度大约是多少千米?
?
怎样解决呢?
教材第52页例2
教材第52页例2
77
方法一:
比例尺
图上距离
在一幅比例尺为1∶30000的地图上,北京地铁2号线的长度大约是77 cm。北京地铁2号线的实际长度大约是多少千米?
?
1∶30000
77
方法一:
1∶30000
教材第52页例2
计算时,要注意单位。
实际距离= 77×30000÷1
= 2310000
2310000 cm = 23.1 km
答:北京地铁2号线的实际长度大约是23.1 km。
解:设北京地铁2号线的实际长度大约是x cm。
77
方法二:
可以用解比例的方法求出实际距离。
2310000 cm = 23.1 km
x
1∶30000
实际距离
77
1∶30000
方法三:
2310000 cm = 23.1 km
观察三种方法,它们的依据是什么?有什么共同点?
实际距离
方法三:
方法二:
方法一:
比例的基本性质
依据:
课堂练习
教材第52页“做一做”
1.先把右图中的线段比例尺改写成数值比例尺,再用直尺量出图中河西村与汽车站之间的距离,并计算出两地的实际距离大约是多少。
600 m = 60000 cm
数值比例尺:1∶60000
3 cm
图上距离:3 cm
教材第52页“做一做”
比例尺:1∶60000
3
1∶60000
1.先把右图中的线段比例尺改写成数值比例尺,再用直尺量出图中河西村与汽车站之间的距离,并计算出两地的实际距离大约是多少。
3 cm
方法一:
解:设两地的实际距离大约是 x cm。
3
1∶60000
x
计算时,要注意单位。
答:两地的实际距离大约是1.8 km。
实际距离
3
方法二:
答:两地的实际距离大约是1.8 km。
2.在比例尺是1∶的地图上,量得武汉到北京的距
离是14.4厘米,北京到武汉的实际距离大约是多少千米?
解:设北京到武汉的实际距离是 x cm 。
14.4
1∶8000000
x
0
3.在一幅中国地图上,选取两个城市。量出它们在图上
的距离,再根据比例尺算出它们的实际距离。
教材第55页第6题
1∶18000000
武汉
杭州
3.1
解:设武汉至杭州的实际距离约为 x cm 。
x
0
答:武汉至杭州的实际距离约为558 km。
3.1 cm
拓展提升
1.在比例尺为1∶2000000的地图上,量得甲地到乙地的距
离是16 cm。如果一辆汽车以每小时50公里的速度从甲地
开往乙地,6小时能到达吗?
先算出甲、乙两地的实际距离,再根据“距离÷速度=时间”来计算所用的时间,最后与6小时进行比较。
1.在比例尺为1∶2000000的地图上,量得甲地到乙地的距
离是16 cm。如果一辆汽车以每小时50公里的速度从甲地
开往乙地,6小时能到达吗?
答:6小时不能到达。
>6
解:设甲、乙两地的实际距离为 x cm 。
16
x
2.如下图,量得宜城至铜陵的高速路距离为12 cm,上午
8:00从宜城出发,什么时候到达铜陵?(车辆平均时速
为100 km/h)
解:设宜城到铜陵的实际距离为x cm 。
1∶6000000
12 cm
12
x
1∶6000000
12 cm
12分
答:15时12分到达铜陵。
2.如下图,量得宜城至铜陵的高速路距离为12 cm,上午
8:00从宜城出发,什么时候到达铜陵?(车辆平均时速
为100 km/h)
6∶1是放大比例尺。
3.在一张比例尺为6∶1精密零件的图纸上,量得零件的
长为24 mm,这个零件的实际长度是多少?
24
6∶1
解:设这个零件的实际长度是 x mm 。
x
答:这个零件的实际长度是4 mm。
课堂小结
这节课你有什么收获?
求实际距离的方法
方程法
1
可知=
算术法
2
1.设未知数x。
根据
2.列比例。
3.解比例。
用除法计算。
转化为求图上距离的几倍是多少来计算。
3
4 比例
3.比例的应用
数学人教版六年级下册
第3课时 比例尺(3)
1.能根据比例尺及相应的条件画出平面图。
2.培养联系实际解决问题的能力,感受数学在生活中的广泛应用。
学习目标
【重点】把比例尺应用到实际生活中,解决实 际问题。
【难点】根据比例尺及相应的条件画平面图。
课堂导入
我想在长4 m,宽3 m,高3 m的书房北面放置一个长2 m,宽1.5 m,高2 m的书架,南面放置一个长1.5 m,宽1 m,高0.8 m的书桌。
你能帮她画出书房的平面设计图吗?
3 m
0.8 m
4 m
3 m
2 m
2 m
1.5 m
1.5 m
1 m
上面哪幅平面设计图设计得更标准?
4 m
3 m
北
书架
书桌
4 m
3 m
北
书架
书桌
√
画出的书架、书桌形状与要求一致。
新知探究
小明家在学校正西方向,距学校200 m;小亮家在小明家正东方向,距小明家400 m;小红家在学校正北方向,距学校250 m。在下图中画出他们三家和学校的位置平面图(比例尺1∶10000)。
教材第53页例3
北
学校
0
( ) m
3
观察题目,说说已知什么 求什么?
还已知比例尺是1∶10000,求的是
他们三家到学校的图上距离。
已知小明家在学校正西方向,距学校200 m;小亮家在小明家正东方向,距小明家400 m;小红家在学校正北方向,距学校250 m。
图上距离
先求图上距离
计算图上距离之前,记得要先把实际距离化成用“cm”作单位的数。
200 m=20000 cm
400 m=40000 cm
250 m=25000 cm
由长度单位间的换算方法可知100 m = 10000 cm。
单位换算
小明家到学校的图上距离:
小红家到学校的图上距离:
小亮家到学校的图上距离:
25000× = 2.5(cm)
(40000 - 20000)× = 2(cm)
20000× = 2(cm)
求图上距离
( ) m
100
小明家
北
学校
0
再画出平面图
小亮家
小明家
学校
( ) m
100
0
北
再画出平面图
小红家
小明家
学校
( ) m
100
0
北
再画出平面图
小亮家
应用比例尺画平面图时,要先根据比例尺和实际距离求出图上距离,再根据距离和方向画出相应的位置,并标明比例尺。
课堂练习
1.学校要建一个长80 m、宽60 m的长方形操场。请在右图中画出操场的平面图(比例尺 1∶2000)。
教材第53页“做一做”
先要算出长和宽
的图上距离。
0
20 m
2000 cm=20 m
80 m=8000 cm
60 m=6000 cm
操场平面图
0
20 m
4 cm
3 cm
1.学校要建一个长80 m、宽60 m的长方形操场。请在右图中画出操场的平面图(比例尺 1∶2000)。
2.两个城市之间的铁路线大约长1900 km。在一幅比例尺为1 : 40000000的地图上,这两个城市之间铁路线的长度大约是多少厘米?
教材第55页“练习十”第7题
1900 km=190000000 cm
答:这两个城市之间铁路线的长度大约是4.75 cm。
3.填表。
教材第55页“练习十”第8题
比例尺 图上距离 实际距离
1∶50000 1.8 km
1∶2000000 450 km
1∶60000000 15 cm
3.6 cm
22.5 cm
9000 km
= 3.6(cm)
= 22.5(cm)
= 900000000(cm) = 9000(km)
先根据图上距离列式。
再根据实际距离=图上距离÷比例尺列式。
4.小明家的正西面100米是商场,商场的正北
面500米是学校,学校的正西面300米是小
红家,小红家的正南面200米是医院。请你
确定比例尺后画出平面图。
北
比例尺1∶20000
小明家
确定比例尺时要考虑哪些数据?
商场
100 m=10000 cm
4.小明家的正西面100米是商场,商场的正北
面500米是学校,学校的正西面300米是小
红家,小红家的正南面200米是医院。请你
确定比例尺后画出平面图。
北
小明家
比例尺1∶20000
4.小明家的正西面100米是商场,商场的正北
面500米是学校,学校的正西面300米是小
红家,小红家的正南面200米是医院。请你
确定比例尺后画出平面图。
学校
商场
500 m=50000 cm
北
比例尺1∶20000
小明家
4.小明家的正西面100米是商场,商场的正北
面500米是学校,学校的正西面300米是小
红家,小红家的正南面200米是医院。请你
确定比例尺后画出平面图。
300 m=30000 cm
小红家
北
比例尺1∶20000
小明家
商场
学校
医院
4.小明家的正西面100米是商场,商场的正北
面500米是学校,学校的正西面300米是小
红家,小红家的正南面200米是医院。请你
确定比例尺后画出平面图。
200 m=20000 cm
北
比例尺1∶20000
小明家
商场
学校
小红家
拓展提升
1.在比例尺为1 ∶ 400000的地图上,甲、乙两地
相距12 cm,现在要画一幅比例尺为1:500000
的地图,甲、乙两地的图上距离是多少厘米?
不论用哪个比例尺,相同两个地方之间的实际距离是不变的。
可以先求出两地之间的实际距离,
再求两地之间的图上距离。
甲、乙两地在比例尺为1∶500000的地图上的距离:
甲、乙两地的实际距离:
12 =4800000(cm)
答:甲、乙两地的图上距离是9.6 cm。
1.在比例尺为1 ∶ 400000的地图上,甲、乙两地
相距12 cm,现在要画一幅比例尺为1:500000
的地图,甲、乙两地的图上距离是多少厘米?
2.量得一个操场的长是800 m,宽是600 m,将其
画在比例尺为1∶40000的图纸上,这个操场的
面积是多少平方厘米?
要想知道这个操场在图纸上的面积,就要先求出这个操场在图纸上的长和宽。
800 m = 80000 cm
600 m = 60000 cm
2.量得一个操场的长是800 m,宽是600 m,将其
画在比例尺为1∶40000的图纸上,这个操场的
面积是多少平方厘米?
操场的图上长度:
80000× = 2(cm)
操场的图上宽度:
60000×= 1.5(cm)
操场的图上面积:
2×1.5 = 3()
答:在图纸上,这个操场的面积是3。
应用比例尺画平面图的步骤
课堂小结
这节课你有什么收获?
3
1
2
根据实际距离与比例尺求出图上距离。
根据图上距离和方向画出相应的平面图,并标明平面图的名称及比例尺。
根据实际距离与纸张的大小确定平面图的比例尺。
Thank you!
