第六单元_第13课时_图形的运动(教学课件)-六年级数学下册人教版(共39张PPT)
文档属性
| 名称 | 第六单元_第13课时_图形的运动(教学课件)-六年级数学下册人教版(共39张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 7.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-05 16:16:15 | ||
图片预览







文档简介
(共39张PPT)
小学数学·六年级(下)·RJ
第13课时 总复习 图形的运动
能运用轴对称、平移、旋转、放大与缩小的特征进行图形的变换。
通过复习,进一步掌握轴对称、平移、旋转、放大与缩小等图形运动的特征。
通过欣赏图形变换所创造出来的美,进一步感受轴对称、平移、旋转、放大与缩小在现实生活中的广泛应用,体会数学的文化价值,感受数学的美。
掌握对称、平移、旋转、放大与缩小的特征,能运用对称、平移、旋转、放大与缩小的特征进行图形的变换。
综合运用对称、平移、旋转、放大与缩小的特征进行图形的变化,进一步发展空间观念。
感受各种图形的运动所创造的美,体会图形运动的价值,激发学习的热情。
通过复习,进一步掌握轴对称、平移、旋转、放大与缩小等图形运动的特征。
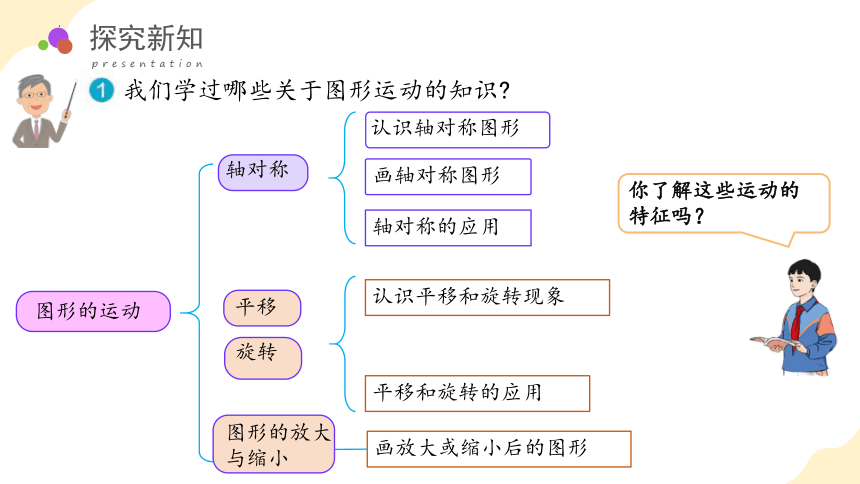
你了解这些运动的特征吗?
我们学过哪些关于图形运动的知识
图形的运动
轴对称
平移
认识轴对称图形
画轴对称图形
轴对称的应用
认识平移和旋转现象
平移和旋转的应用
旋转
图形的放大与缩小
画放大或缩小后的图形
你知道轴对称和对称轴的区别吗?
图形的运动
如果一个图形沿着一条直线对折,两侧的图形能够完全重合,这个图形叫做轴对称图形,折痕所在的这条直线叫做对称轴。
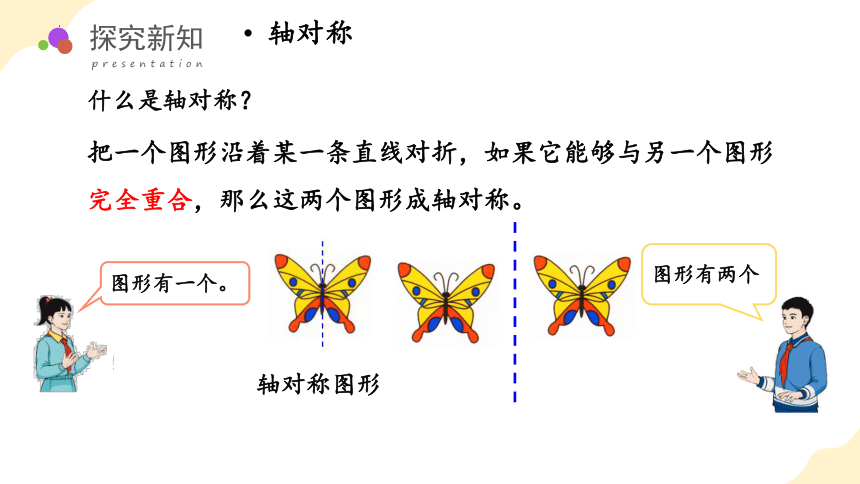
什么是轴对称图形?
把一个图形沿着某一条直线对折,如果它能够与另一个图形完全重合,那么这两个图形成轴对称。
什么是轴对称?
轴对称
图形有一个。
轴对称图形
图形有两个
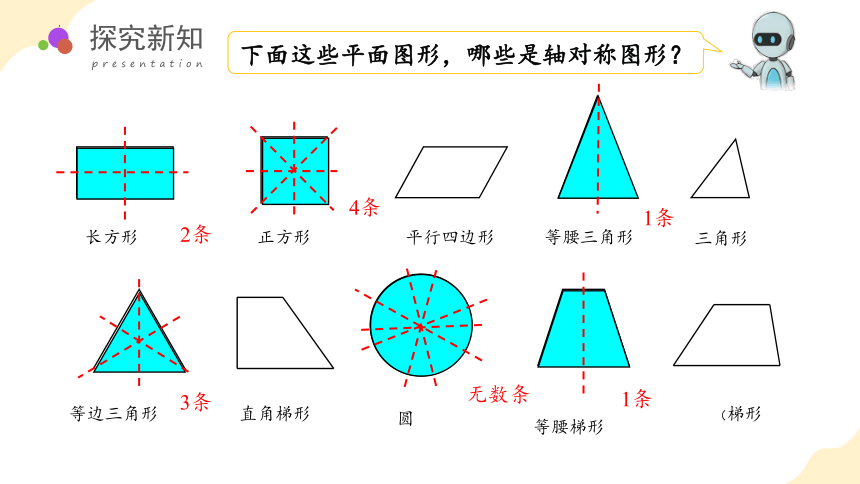
下面这些平面图形,哪些是轴对称图形?
无数条
长方形
正方形
平行四边形
等腰三角形
三角形
等边三角形
直角梯形
圆
等腰梯形
(梯形
2条
4条
1条
3条
1条
轴对称
常见的图形有多少条对称轴?
B
C
D
B′
C′
·
·
·
D′
E′
·
E
F
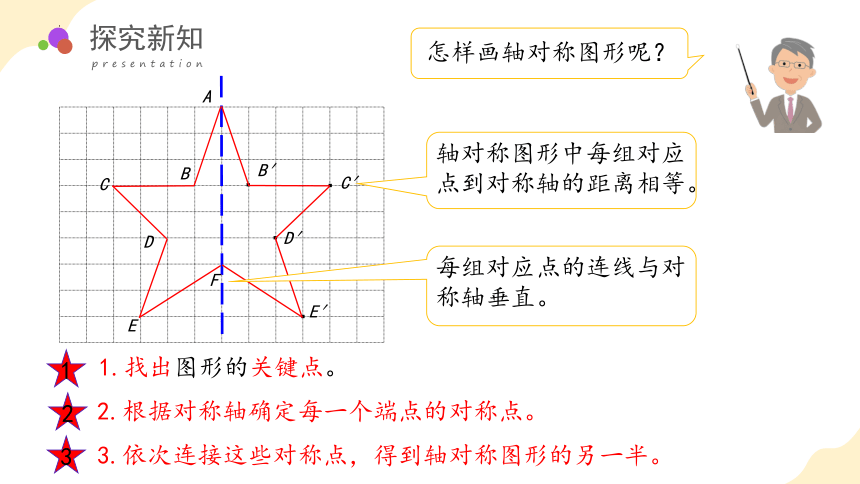
每组对应点的连线与对称轴垂直。
轴对称图形中每组对应点到对称轴的距离相等。
A
1.找出图形的关键点。
1
2.根据对称轴确定每一个端点的对称点。
2
3.依次连接这些对称点,得到轴对称图形的另一半。
3
怎样画轴对称图形呢?
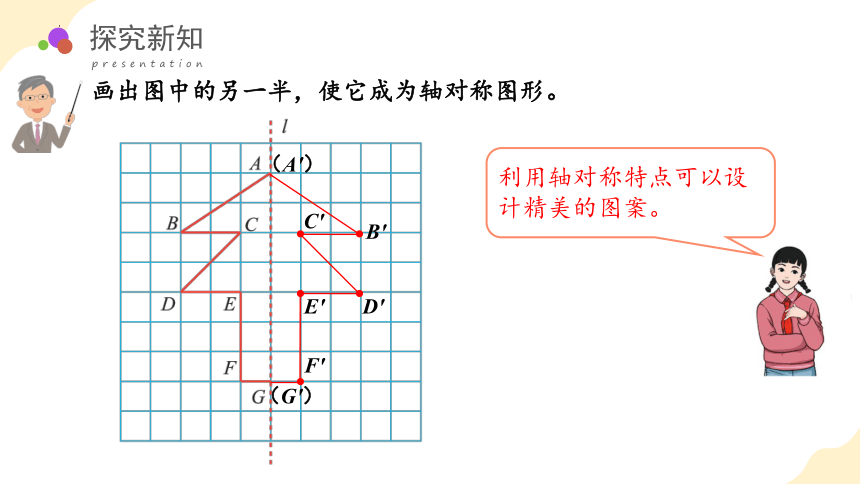
画出图中的另一半,使它成为轴对称图形。
B'
C'
D'
E'
F'
(G')
(A')
利用轴对称特点可以设计精美的图案。
平移与旋转
什么是平移?什么是旋转?
物体或图形沿着直线运动的现象是平移。
物体或图形绕着一个点或一个轴运动的现象是旋转。
旋转的方法是什么?
1.弄清旋转中心 (绕哪一点旋转);
2.弄清旋转方向(顺时针或逆时针);
3.弄清旋转角度;
4.分别旋转各边,画出各顶点的对应点,再连线。
平移与旋转
旋转三要素:旋转中心、旋转方向和旋转角度
画出这个图形绕O点按逆时针方向旋转90°后的图形。
O
平移与旋转
平移的方法是什么?
1.弄清平移的方向(上、下、左、右);
2.弄清平移的距离(格数);
3.分别平移各顶点,画出各顶点的对应点,再相连。
画出 向右平移4格后得到的图形。
弄清方向
弄清距离
描点连线
平移后的图形:大小、方向、形状不变,位置发生变化。
平移和旋转
选点:在原图形上选择关键点。
移点:按要求把关键点向规定的方向平移规定的格数。
最后把这些点顺次连接起来。
如何画平移后的图形?
图形的放大与缩小的意义是什么?
把一个图形的各边按一定的比扩大或缩小,从而得到该图形的放大图或缩小图。
画一个图形的放大图或缩小图的步骤:
先按给定的比计算出放大图或缩小图相对应的各边长度,
再按新边长画出原图形的放大图或缩小图。
图形的放大与缩小
先按1∶3把下面的三角形缩小,再把缩小后的图形按2∶1放大。
确定比例
计算新图形边长
画出新图形
.
5 4 3 2 1
1 2 3 4 5
1
1
平移
旋转
轴对称
放大或缩小
仔细观察、认真分类:
1.这些运动方式有什么相同和不同之处?
2.如果把这些图形运动的方式分成两类,你会怎样分?
我们学过哪些关于图形运动的知识
哪些运动不改变图形的形状和大小?哪些运动只改变图形的大小,而不改变形状?
平移、旋转和轴对称不改变图形的形状和大小。
图形的放大和缩小只改变大小,不改变形状。
哪些运动不改变图形的形状和大小,哪些运动只改变图形的大小,而不改变形状?
图形的运动特征
平 移
轴对称
旋 转
图形的放大和缩小
特征
形状
大小
改变
图形的运动
位置
000000000000000000
不变
不变
000000000000000000
改变
在平面图形整理活动中,了解和掌握直线、射线、线段、角、垂线和平行线的特征以及三角形、四边形和圆等平面图形的特征。
图形的运动
你知道这些图案分别用什么方法设计出来的吗?
利用图形的运动设计图案。
A
B
C
(1)利用图形的不断旋转可以设计美丽的图案。
图形的运动
(2)利用图形的不断平移也可以设计美丽的图案。
图形的运动
A:图案是用轴对称的方法设计的。
B:图案是用旋转的方法设计的。
C:图案是按比例放大的方法把B图案扩大,并通过平移设计的。
图形的运动
利用轴对称、平移、旋转设计美丽图案。
D
C
A
O
B
在生活中轴对称、平移、旋转应用的非常广泛。
达标练习,巩固成果
1.图中从A→B→C→D是怎样变化的?(教材P91 做一做 )
(1)A经过向右平移5个格得到B。
(2)B先向右平移5个格,再绕中心点逆时针旋转90°得到C 。或者先逆时针旋转90°,再向右平移5个格得到C。
A B C D
1.图中A→B→C→D是怎样变过来的?(教材P91 做一做 )
(3)C先向右平移5个格,再绕中心点逆时针旋转90°得到D。或者先绕中心点旋转90°,在向右平移5个格得到D。
A B C D
2.下面哪些图形是轴对称图形?画出它们的对称轴。(教材P92 练习十九 第1题 )
3.根据给定的对称轴画出图形的另一半。(教材P92 练习十九 第2题 )
4.下面4个图形的涂色部分面积相等吗?为什么?(教材P92 练习十九 第4题 )
相等。因为这四个图形的涂色部分面积等于一个大圆面积减去一个中间圆的面积,再加上一个小圆的面积的和。
5. 以点A为中心,将图形按逆时针方向旋转90°,画出旋转后的图形。
6. 画出原图形按2∶1放大后的图形。
7. 按要求在下面的方格纸上画一画。
(1)画出三角形绕点O按顺时针方向旋转90°后的图形。
(2)画出右面图形的另一半,使它成为轴对称图形。
(3)画出与三角形面积相等的平行四边形和梯形各1个。
8.画一画。
(1)画出小旗子向左平移8格后的图形A。
(2)画出小旗子绕点О按顺时针方向旋转90°后的图形B。
(3)画出小旗子按2∶1放大后的图形C。
A
B
C
9.下面6个同样的正方形中,涂色部分的面积一样大吗?为什么?
【答案】涂色部分的面积一样大。观察图可知,六个图形的空白部分均可组成一个半径相等的圆,又因为正方形面积相等,所以正方形面积减去圆的面积的差也相等,也就是涂色部分的面积相等。
这节课你有什么收获?
1.平移、旋转和轴对称不改变图形的形状和大小;
3.图形的放大和缩小只改变大小,不改变形状。
①先确定扩大或缩小的比。
②再确定格数。
③画图。
2.作图步骤:
4.作图步骤:
① 先找关键点。
②再找对称点。
③连线。
小学数学·六年级(下)·RJ
第13课时 总复习 图形的运动
能运用轴对称、平移、旋转、放大与缩小的特征进行图形的变换。
通过复习,进一步掌握轴对称、平移、旋转、放大与缩小等图形运动的特征。
通过欣赏图形变换所创造出来的美,进一步感受轴对称、平移、旋转、放大与缩小在现实生活中的广泛应用,体会数学的文化价值,感受数学的美。
掌握对称、平移、旋转、放大与缩小的特征,能运用对称、平移、旋转、放大与缩小的特征进行图形的变换。
综合运用对称、平移、旋转、放大与缩小的特征进行图形的变化,进一步发展空间观念。
感受各种图形的运动所创造的美,体会图形运动的价值,激发学习的热情。
通过复习,进一步掌握轴对称、平移、旋转、放大与缩小等图形运动的特征。
你了解这些运动的特征吗?
我们学过哪些关于图形运动的知识
图形的运动
轴对称
平移
认识轴对称图形
画轴对称图形
轴对称的应用
认识平移和旋转现象
平移和旋转的应用
旋转
图形的放大与缩小
画放大或缩小后的图形
你知道轴对称和对称轴的区别吗?
图形的运动
如果一个图形沿着一条直线对折,两侧的图形能够完全重合,这个图形叫做轴对称图形,折痕所在的这条直线叫做对称轴。
什么是轴对称图形?
把一个图形沿着某一条直线对折,如果它能够与另一个图形完全重合,那么这两个图形成轴对称。
什么是轴对称?
轴对称
图形有一个。
轴对称图形
图形有两个
下面这些平面图形,哪些是轴对称图形?
无数条
长方形
正方形
平行四边形
等腰三角形
三角形
等边三角形
直角梯形
圆
等腰梯形
(梯形
2条
4条
1条
3条
1条
轴对称
常见的图形有多少条对称轴?
B
C
D
B′
C′
·
·
·
D′
E′
·
E
F
每组对应点的连线与对称轴垂直。
轴对称图形中每组对应点到对称轴的距离相等。
A
1.找出图形的关键点。
1
2.根据对称轴确定每一个端点的对称点。
2
3.依次连接这些对称点,得到轴对称图形的另一半。
3
怎样画轴对称图形呢?
画出图中的另一半,使它成为轴对称图形。
B'
C'
D'
E'
F'
(G')
(A')
利用轴对称特点可以设计精美的图案。
平移与旋转
什么是平移?什么是旋转?
物体或图形沿着直线运动的现象是平移。
物体或图形绕着一个点或一个轴运动的现象是旋转。
旋转的方法是什么?
1.弄清旋转中心 (绕哪一点旋转);
2.弄清旋转方向(顺时针或逆时针);
3.弄清旋转角度;
4.分别旋转各边,画出各顶点的对应点,再连线。
平移与旋转
旋转三要素:旋转中心、旋转方向和旋转角度
画出这个图形绕O点按逆时针方向旋转90°后的图形。
O
平移与旋转
平移的方法是什么?
1.弄清平移的方向(上、下、左、右);
2.弄清平移的距离(格数);
3.分别平移各顶点,画出各顶点的对应点,再相连。
画出 向右平移4格后得到的图形。
弄清方向
弄清距离
描点连线
平移后的图形:大小、方向、形状不变,位置发生变化。
平移和旋转
选点:在原图形上选择关键点。
移点:按要求把关键点向规定的方向平移规定的格数。
最后把这些点顺次连接起来。
如何画平移后的图形?
图形的放大与缩小的意义是什么?
把一个图形的各边按一定的比扩大或缩小,从而得到该图形的放大图或缩小图。
画一个图形的放大图或缩小图的步骤:
先按给定的比计算出放大图或缩小图相对应的各边长度,
再按新边长画出原图形的放大图或缩小图。
图形的放大与缩小
先按1∶3把下面的三角形缩小,再把缩小后的图形按2∶1放大。
确定比例
计算新图形边长
画出新图形
.
5 4 3 2 1
1 2 3 4 5
1
1
平移
旋转
轴对称
放大或缩小
仔细观察、认真分类:
1.这些运动方式有什么相同和不同之处?
2.如果把这些图形运动的方式分成两类,你会怎样分?
我们学过哪些关于图形运动的知识
哪些运动不改变图形的形状和大小?哪些运动只改变图形的大小,而不改变形状?
平移、旋转和轴对称不改变图形的形状和大小。
图形的放大和缩小只改变大小,不改变形状。
哪些运动不改变图形的形状和大小,哪些运动只改变图形的大小,而不改变形状?
图形的运动特征
平 移
轴对称
旋 转
图形的放大和缩小
特征
形状
大小
改变
图形的运动
位置
000000000000000000
不变
不变
000000000000000000
改变
在平面图形整理活动中,了解和掌握直线、射线、线段、角、垂线和平行线的特征以及三角形、四边形和圆等平面图形的特征。
图形的运动
你知道这些图案分别用什么方法设计出来的吗?
利用图形的运动设计图案。
A
B
C
(1)利用图形的不断旋转可以设计美丽的图案。
图形的运动
(2)利用图形的不断平移也可以设计美丽的图案。
图形的运动
A:图案是用轴对称的方法设计的。
B:图案是用旋转的方法设计的。
C:图案是按比例放大的方法把B图案扩大,并通过平移设计的。
图形的运动
利用轴对称、平移、旋转设计美丽图案。
D
C
A
O
B
在生活中轴对称、平移、旋转应用的非常广泛。
达标练习,巩固成果
1.图中从A→B→C→D是怎样变化的?(教材P91 做一做 )
(1)A经过向右平移5个格得到B。
(2)B先向右平移5个格,再绕中心点逆时针旋转90°得到C 。或者先逆时针旋转90°,再向右平移5个格得到C。
A B C D
1.图中A→B→C→D是怎样变过来的?(教材P91 做一做 )
(3)C先向右平移5个格,再绕中心点逆时针旋转90°得到D。或者先绕中心点旋转90°,在向右平移5个格得到D。
A B C D
2.下面哪些图形是轴对称图形?画出它们的对称轴。(教材P92 练习十九 第1题 )
3.根据给定的对称轴画出图形的另一半。(教材P92 练习十九 第2题 )
4.下面4个图形的涂色部分面积相等吗?为什么?(教材P92 练习十九 第4题 )
相等。因为这四个图形的涂色部分面积等于一个大圆面积减去一个中间圆的面积,再加上一个小圆的面积的和。
5. 以点A为中心,将图形按逆时针方向旋转90°,画出旋转后的图形。
6. 画出原图形按2∶1放大后的图形。
7. 按要求在下面的方格纸上画一画。
(1)画出三角形绕点O按顺时针方向旋转90°后的图形。
(2)画出右面图形的另一半,使它成为轴对称图形。
(3)画出与三角形面积相等的平行四边形和梯形各1个。
8.画一画。
(1)画出小旗子向左平移8格后的图形A。
(2)画出小旗子绕点О按顺时针方向旋转90°后的图形B。
(3)画出小旗子按2∶1放大后的图形C。
A
B
C
9.下面6个同样的正方形中,涂色部分的面积一样大吗?为什么?
【答案】涂色部分的面积一样大。观察图可知,六个图形的空白部分均可组成一个半径相等的圆,又因为正方形面积相等,所以正方形面积减去圆的面积的差也相等,也就是涂色部分的面积相等。
这节课你有什么收获?
1.平移、旋转和轴对称不改变图形的形状和大小;
3.图形的放大和缩小只改变大小,不改变形状。
①先确定扩大或缩小的比。
②再确定格数。
③画图。
2.作图步骤:
4.作图步骤:
① 先找关键点。
②再找对称点。
③连线。
