人教版四年级下册数学第五单元《三角形内角和》(课件)(共16张PPT)
文档属性
| 名称 | 人教版四年级下册数学第五单元《三角形内角和》(课件)(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 10.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-02 00:00:00 | ||
图片预览



文档简介
(共16张PPT)
三角形的内角和
人教版四年级下册第五单元
你还记得三角形有几个内角吗?
谈话导入,提出猜想
1
2
3
猜想:
任意三角形的内角和是180°
?
谈话导入,提出猜想
小组合作要求:
1.四人为一小组,先交流方法再动手操作;
2.利用现有的学具选择你喜欢的方式进行验证;
3.小组内交流,得出结论;
4.汇报。
(选了什么三角形—用了什么方法验证—得出什么结论)
合作探究,验证猜想
拼
折
59
58
57
56
55
54
53
52
51
50
49
48
47
46
45
44
43
42
41
40
39
38
37
36
35
34
33
32
31
30
29
28
27
26
25
24
23
22
21
20
19
18
17
16
15
14
13
12
11
10
09
08
07
06
05
04
03
02
01
00
00
01
:
开始/重置
00
59
58
57
56
55
54
53
52
51
50
49
48
47
46
45
44
43
42
41
40
39
38
37
36
35
34
33
32
31
30
29
28
27
26
25
24
23
22
21
20
19
18
17
16
15
14
13
12
11
10
09
08
07
06
05
04
03
02
01
00
02
03
59
58
57
56
55
54
53
52
51
50
49
48
47
46
45
44
43
42
41
40
39
38
37
36
35
34
33
32
31
30
29
28
27
26
25
24
23
22
21
20
19
18
17
16
15
14
13
12
11
10
09
08
07
06
05
04
03
02
01
00
04
59
58
57
56
55
54
53
52
51
50
49
48
47
46
45
44
43
42
41
40
39
38
37
36
35
34
33
32
31
30
29
28
27
26
25
24
23
22
21
20
19
18
17
16
15
14
13
12
11
10
09
08
07
06
05
04
03
02
01
00
05
59
58
57
56
55
54
53
52
51
50
49
48
47
46
45
44
43
42
41
40
39
38
37
36
35
34
33
32
31
30
29
28
27
26
25
24
23
22
21
20
19
18
17
16
15
14
13
12
11
10
09
08
07
06
05
04
03
02
01
00
1
2
3
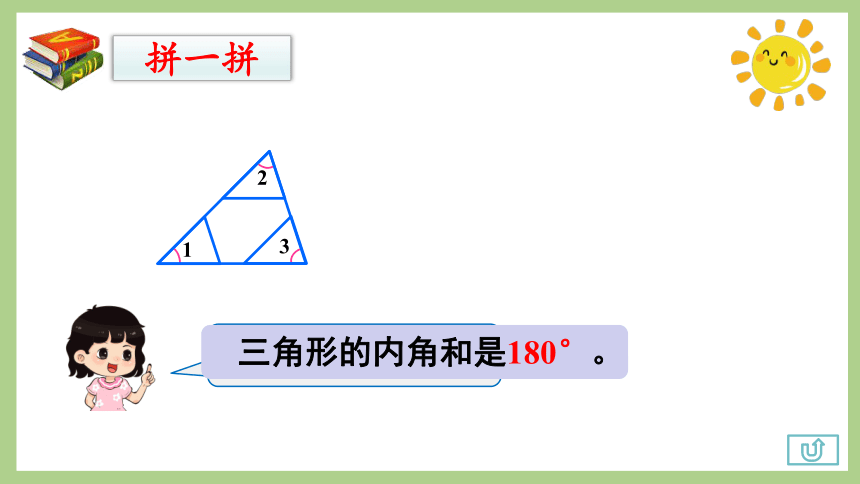
拼成了一个平角。
三角形的内角和是180°。
拼一拼
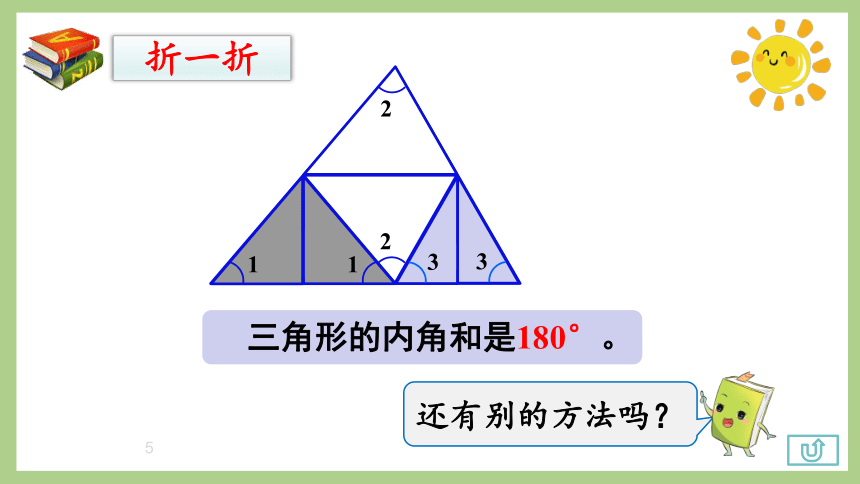
还有别的方法吗?
2
2
1
1
3
3
三角形的内角和是180°。
折一折
5
推理说明
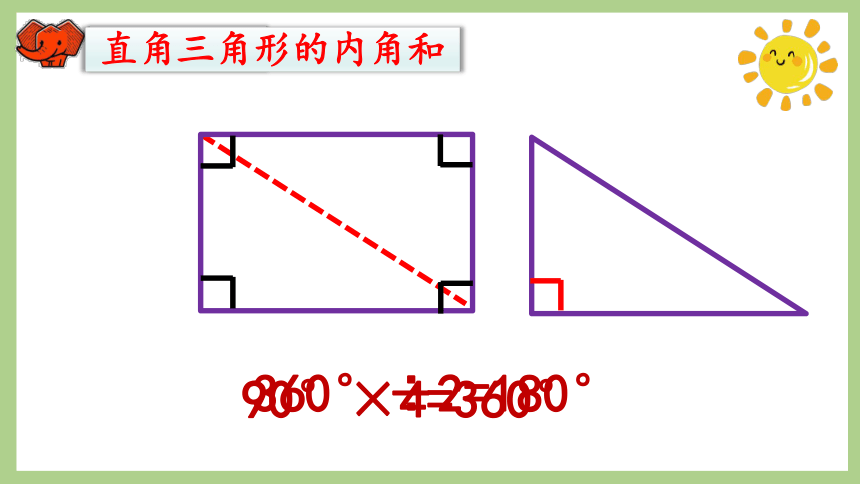
90°×4=360°
直角三角形的内角和
360°÷2=180°
180°+180°-90°-90°=180°
锐角三角形的内角和
180°+180°-90°-90°=180°
钝角三角形的内角和
帕斯卡:法国的数学家、物理学家,为人类创造了无数的奇迹,早在300年前这位法国著名的科学家就已经发现了:任何三角形的内角和都是180°,而他当时才12岁。
数学文化
猜想:
任意三角形的内角和是180°
?
结论:
几何画板.gsp
1.下面哪一组角能组成三角形?请说一说你的理由。
90°+40°+50°=180°
20°+40°+120°=180°
知识巩固,内化提升
(1)90°,40°,50
(2)20°,40°,120°
(3)35°,70°,80°
35°+70°+80°=185°
2. 在下图中,∠1=140°,∠3=25°。求∠2的度数。
∠1+∠2+∠3=180°
∠2=180°- ∠1- ∠3
=180°- 140°- 25°
=15°
3.爸爸给小红买了一个等腰三角形的风筝。风筝的一个底角是70°,风筝的顶角是多少度?
180°-70°× 2=40°
答:风筝的顶角是40°。
学科融合,拓展延伸
回顾反思,课堂小结
这节课你有什么收获
三角形的内角和
人教版四年级下册第五单元
你还记得三角形有几个内角吗?
谈话导入,提出猜想
1
2
3
猜想:
任意三角形的内角和是180°
?
谈话导入,提出猜想
小组合作要求:
1.四人为一小组,先交流方法再动手操作;
2.利用现有的学具选择你喜欢的方式进行验证;
3.小组内交流,得出结论;
4.汇报。
(选了什么三角形—用了什么方法验证—得出什么结论)
合作探究,验证猜想
拼
折
59
58
57
56
55
54
53
52
51
50
49
48
47
46
45
44
43
42
41
40
39
38
37
36
35
34
33
32
31
30
29
28
27
26
25
24
23
22
21
20
19
18
17
16
15
14
13
12
11
10
09
08
07
06
05
04
03
02
01
00
00
01
:
开始/重置
00
59
58
57
56
55
54
53
52
51
50
49
48
47
46
45
44
43
42
41
40
39
38
37
36
35
34
33
32
31
30
29
28
27
26
25
24
23
22
21
20
19
18
17
16
15
14
13
12
11
10
09
08
07
06
05
04
03
02
01
00
02
03
59
58
57
56
55
54
53
52
51
50
49
48
47
46
45
44
43
42
41
40
39
38
37
36
35
34
33
32
31
30
29
28
27
26
25
24
23
22
21
20
19
18
17
16
15
14
13
12
11
10
09
08
07
06
05
04
03
02
01
00
04
59
58
57
56
55
54
53
52
51
50
49
48
47
46
45
44
43
42
41
40
39
38
37
36
35
34
33
32
31
30
29
28
27
26
25
24
23
22
21
20
19
18
17
16
15
14
13
12
11
10
09
08
07
06
05
04
03
02
01
00
05
59
58
57
56
55
54
53
52
51
50
49
48
47
46
45
44
43
42
41
40
39
38
37
36
35
34
33
32
31
30
29
28
27
26
25
24
23
22
21
20
19
18
17
16
15
14
13
12
11
10
09
08
07
06
05
04
03
02
01
00
1
2
3
拼成了一个平角。
三角形的内角和是180°。
拼一拼
还有别的方法吗?
2
2
1
1
3
3
三角形的内角和是180°。
折一折
5
推理说明
90°×4=360°
直角三角形的内角和
360°÷2=180°
180°+180°-90°-90°=180°
锐角三角形的内角和
180°+180°-90°-90°=180°
钝角三角形的内角和
帕斯卡:法国的数学家、物理学家,为人类创造了无数的奇迹,早在300年前这位法国著名的科学家就已经发现了:任何三角形的内角和都是180°,而他当时才12岁。
数学文化
猜想:
任意三角形的内角和是180°
?
结论:
几何画板.gsp
1.下面哪一组角能组成三角形?请说一说你的理由。
90°+40°+50°=180°
20°+40°+120°=180°
知识巩固,内化提升
(1)90°,40°,50
(2)20°,40°,120°
(3)35°,70°,80°
35°+70°+80°=185°
2. 在下图中,∠1=140°,∠3=25°。求∠2的度数。
∠1+∠2+∠3=180°
∠2=180°- ∠1- ∠3
=180°- 140°- 25°
=15°
3.爸爸给小红买了一个等腰三角形的风筝。风筝的一个底角是70°,风筝的顶角是多少度?
180°-70°× 2=40°
答:风筝的顶角是40°。
学科融合,拓展延伸
回顾反思,课堂小结
这节课你有什么收获
