高中数学人教A版(2019)必修2 9.2.2 总体百分位数的估计(24页ppt)
文档属性
| 名称 | 高中数学人教A版(2019)必修2 9.2.2 总体百分位数的估计(24页ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-06 08:48:59 | ||
图片预览








文档简介
(共24张PPT)
第九章
9.2.2 总体百分位数的估计
人教A版(2019)
教学目标
学习目标 数学素养
1.正确理解第p百分位数的概念,掌握第p百分位数的求法. 1.数据分析素养.
2.能用样本估计整体百分位数. 2.数据分析素养和运算素养.
知新引入
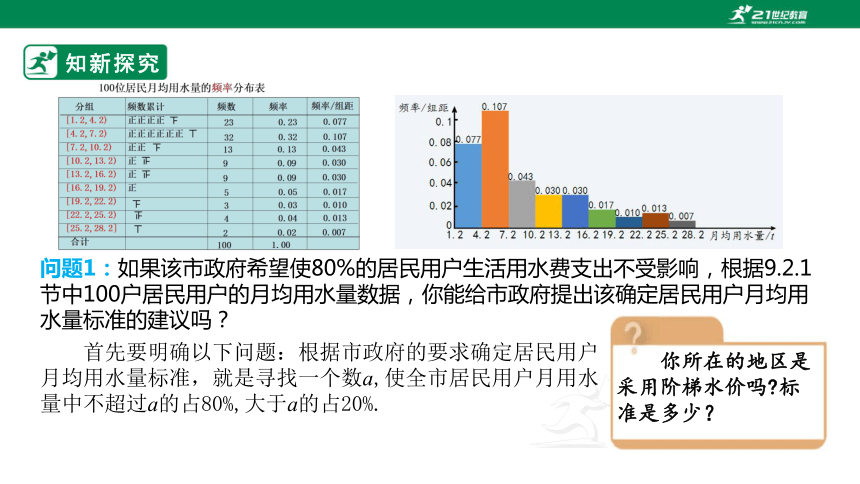
前面我们用频率分布表、频率分布直方图描述了居民用户月均用水量的样本数据,通过对图表的观察与分析,得出了一些样本数据的频率分布规律,由此推测了该市全体居民用户月均用水量的分布情况,得出了“大部分居民用户的月均用水量集中在一个较低值区域”等推断. 接下来的问题是,如何利用这些信息,为政府决策服务呢?下面我们对此进行讨论.
如下数据为某市通过随机抽样获得的100户居民月均用水量按从小到大的顺序排列的一组数据(单位:t)
1.3 1.3 1.8 2.0 2.0 2.0 2.0 2.1 2.2 2.3 2.3 2.4 2.6 2.6 3.0 3.2 3.2 3.6 3.6 3.7 3.8 4.0 4.1 4.3 4.4 4.6 4.7 4.9 4.9 4.9 5.1 5.1 5.1 5.2 5.3 5.4 5.4 5.5 5.5 5.5 5.5 5.6 5.7 5.7 5.9 6.0 6.0 6.4 6.4 6.8 6.8 7.0 7.1 7.1 7.1 7.5 7.7 7.8 7.8 7.9 8.1 8.6 8.8 9.0 9.5 9.9 10.0 10.1 10.2 10.2 10.5 10.8 11.1 11.2 12.0 12.0 12.4 13.3 13.6 13.6 13.8 13.8 14.0 14.9 15.7 16.0 16.7 16.8 17.0 17.9 18.3 19.4 20.5 21.6 22.2 22.4 24.3 24.5 25.6 28.0
知新探究
问题1:如果该市政府希望使80%的居民用户生活用水费支出不受影响,根据9.2.1节中100户居民用户的月均用水量数据,你能给市政府提出该确定居民用户月均用水量标准的建议吗?
首先要明确以下问题:根据市政府的要求确定居民用户
月均用水量标准,就是寻找一个数a,使全市居民用户月用水量中不超过a的占80%,大于a的占20%.
你所在的地区是采用阶梯水价吗 标准是多少?
知新探究
下面我们通过样本数据对a的值进行估计.
1.3 1.3 1.8 2.0 2.0 2.0 2.0 2.1 2.2 2.3 2.3 2.4 2.6 2.6 3.0 3.2 3.2 3.6 3.6 3.7 3.8 4.0 4.1 4.3 4.4 4.6 4.7 4.9 4.9 4.9 5.1 5.1 5.1 5.2 5.3 5.4 5.4 5.5 5.5 5.5 5.5 5.6 5.7 5.7 5.9 6.0 6.0 6.4 6.4 6.8 6.8 7.0 7.1 7.1 7.1 7.5 7.7 7.8 7.8 7.9 8.1 8.6 8.8 9.0 9.5 9.9 10.0 10.1 10.2 10.2 10.5 10.8 11.1 11.2 12.0 12.0 12.4 13.3 13.6 13.6 13.8 13.8 14.0 14.9 15.7 16.0 16.7 16.8 17.0 17.9 18.3 19.4 20.5 21.6 22.2 22.4 24.3 24.5 25.6 28.0
把100样本数据按从小到大的顺序排列,得到第80个和第81个数据分别为13.6和13.8.可以发现,区间[13.6,13.8)内的任意一个数,都能把样本数据分成符合条件的两部分.一般地,我们取这两个数的平均数=13.7,并称此数为这组数据的第80百分位数(percentile),或80%分位数.
知新探究
根据样本数据的第80百分位数,我们可以估计总体数据的第80百分位数为13.7左右.由于样本的取值规律与总体的取值规律之间存在偏差,而在决策问题中,只要临界值近似为第80百分位数即可,因此为了实际中操作方便,可以建议市政府把月均用水量标准定为14.0t,或者把年用水量标准定为168t.
你认为14.0t这个标准一定能够保证80%居民不超标准吗?如果不一定,那么哪些环节可能会导致结论的差别
一般地,一组数据的第p百分位数是这样一个值,它使得这组数据中至少有p%的数据小于或等于这个值,且至少有(100-p)%的数据大于或等于这个值.
知新探究
一般地,一组数据的第p百分位数是这样一个值,它使得这组数据中至少有p%的数据小于或等于这个值,且至少有(100-p)%的数据大于或等于这个值.
可以通过下面的步骤计算一组n个数据的第p百分位数:
第1步:按从小到大排列原始数据.
第2步:计算i=n×p%.
第3步:若i不是整数,而大于i的比邻整数为j,则第p百分位数为第j项数据;
若i是整数,则第p百分位数是第i项与第(i+1)项数据的平均数.
对于任意一组数据,满足第p百分位数定义的值可能不唯一. 计算百分位数的方法有多种,我们取一种计算方法比较简单的.
知新探究
我们在初中学过的中位数,相当于第50百分位数.
在实际应用中,除了中位数外,常用的分位数还有第25百分位数,第75百分位数,这三个分位数把一组由小到大排列后的数据分成四等份,因此称为四分位数.
其中第25百分位数也称为第一四分位数或下四分位数等,第75百分位数也称为第三四分位数或上四分位数等.
另外,像第1百分位数,第5百分位数,第95百分位数和第99百分位数在统计中也经常被应用.
25%
第一四分位数
(下四分位数)
50%
75%
中位数
第三四分位数
(上四分位数)
知新探究
百分位数的特点
⑴第0百分位数是数据组中的最小数,第100百分位数是数据组中的最大数;
⑵一组数据的第p百分位数可能是这组数据中的数,也可能不是这组数据中的数;
⑶一组数据中的某些百分位数可能是同一个数.
知新探究
【例1】根据9.1.2节问题3树人中学高一年级女生的样本数据:
估计树人中学高一年级女生的第25,50,75百分位数.
163.0 164.0 161.0 157.0 162.0 165.0 158.0 155.0 164.0 162.5
154.0 154.0 164.0 149.0 159.0 151.0 170.0 171.0 155.0 148.0
172.0 162.5 158.0 155.5 157.0 163.0 172.0
解:
把27名女生的样本数据按从小到大排序,可得
148.0 149.0 154.0 154.0 155.0 155.0 155.5 157.0 157.0
158.0 158.0 159.0 161.0 161.0 162.0 162.5 162.5 163.0
163.0 164.0 164.0 164.0 165.0 170.0 171.0 172.0 172.0
由25%×27=6.75,50%×27=13.5,75%×27=20.25,
可知样本数据的第25,50,75百分位数为第7,14,21项数据,分别为155.5,161,164.
据此可以估计树人中学高一年级女生的第25,50,75百分位数分别约为155.5,161和164.
由于女生的样本量比较小,所以这里对总体的估计可能会存在比较大的误差.
知新探究
【例2】根据9.2.1表(下表)估计月均用水量的样本数据的80%和95%分位数.
解:
分组 频数 频率
[1.2,4.2) 23 0.23
[4.2,7.2) 32 0.32
[7.2,10.2) 13 0.13
[10.2,13.2) 9 0.09
[13.2,16.2) 9 0.09
[16.2,19.2) 5 0.05
[19.2,22.2) 3 0.03
[22.2,25.2) 4 0.04
[25.2,28.2) 2 0.02
合计 100 1.00
由表可知,月均用水量在13.2t以下的居民用户所占比例为
23%+32%+13%+9%=77%,
在16.2t以下的居民用户所占比例为
77%+9%=86%,
分析:在某些情况下,我们只能获得整理好的统计表或统计图,与原始数据相比,它们损失了一些信息,由表可知在[16.2,19.2)内有5个数据,但不知道这5个数据具体是多少.此时,通常把它们均匀地分布在此区间上.
知新探究
【例2】根据9.2.1表(下表)估计月均用水量的样本数据的80%和95%分位数.
分组 频数 频率
[1.2,4.2) 23 0.23
[4.2,7.2) 32 0.32
[7.2,10.2) 13 0.13
[10.2,13.2) 9 0.09
[13.2,16.2) 9 0.09
[16.2,19.2) 5 0.05
[19.2,22.2) 3 0.03
[22.2,25.2) 4 0.04
[25.2,28.2) 2 0.02
合计 100 1.00
月均用水量在13.2t以下的居民用户所占比例为
23%+32%+13%+9%=77%,
在16.2t以下的居民用户所占比例为
77%+9%=86%,
因此,80%分位数一定位于[13.2,16.2)内
由 13.2+3×=14.2.
可以估计月均用水量的样本数据的80%分位数约为14.2.
类似地,由 22.2+3×=22.95.
可以估计月均用水量的样本数据的95%分位数约为22.95.
知新探究
【例3】某经销商从外地一水殖厂购进一批小龙虾,并随机抽取40只进行统计,按重量分类统计结果如图:
⑴估计这批小龙虾重量的第10百分位数与第90百分位数.
⑵该经销商将这批小龙虾分成三个等级,如上表,则这批小龙虾划为几等品比较合理?
等级 三等品 二等品 一等品
重量(克) [5,25) [25,5) [45,55]
知新探究
解:
⑴因为40×10%=4,所以第10百分位数为第4项与第5项的平均数,
在[5,15)范围内约为=10,
因为40×90%=36,所以第90百分位数为第36项与第37项的平均数,
在[35,55]范围内,约为=45,
⑵由⑴知,将这批小龙虾重量集中在[10,45]范围内,所以划为二等品比较合理.
所以估计这批小龙虾重量的第10百分位数为10,第90百分位数为45.
初试身手
1.初三(2)班有学生42人,一次数学段考成绩如下:28、28、30、32、35、45、
56、56、58、60、61、61、62、64、64、66、76、76、78、80、80、84、86、87、
87、88、89、90、90、92、92、92、94、94、96、96、97、97、97、99、100、100.则第80百分位数是( )分
A.56 B.57 C.94 D.95
解:
由42×80%=33.6,所以取第34位为94分,则第80百分位数是94分.故选C.
C
初试身手
2.西安地铁2号线某机车某日10时从草滩站驶往安远门站的过程中,10个车站上车的人数统计如下:70,60,60,50,60,40,40,30,30,10,则这组数据的第25百分位数、第50百分位数的和为( )
A.90 B.75 C.70 D.65
解:
数据从大到小排列如下:70,60,60,60,50,40,40,30,30,10.
因为10×25%=2.5,按从小到大排列后,第25百分位数是第3项,即30;
第50百分位数即中位数是=45,
所以第25百分位数、第50百分位数的和为75.故选B.
B
初试身手
3.如图所示是一样本的频率分布直方图,样本数据共分3组,
分别为[5,10),[10,15),[15,20].估计样本数据的
第60百分位数是( )
A.14 B.15 C.16 D.17
解:
由频率分布直方图知,第1组的频率为0.04×5=0.2;
第2组的频率为0.10×5=0.5;
设样本数据的第60百分位数是x,
则0.2+0.10(x﹣10)=0.6,解得x=14,
所以估计样本数据的第60百分位数是14.
A
初试身手
4.为了实现绿色发展,避免浪费能源,某市政府计划对居民用电采用阶梯式收费的方法。为此,相关部门在该市随机调查了100户居民六月份的用电量(单位:kW·h),以了解这个城市家庭用电量的情况。数据如下:
8 22 42 49 51 57 60 61 62 63 65 67 70 71 72 76 77 78 80 82 83 84 88 90 93 94 96 96 98 98 100 100 101 105 106 107 107 108 109 110 110 112 113 115 118 120 121 124 127 130 130 131 132 133 134 134 135 135 137 138 139 141 144 146 148 151 154 159 162 163 165 169 170 174 177 178 182 187 191 192 194 201 202 203 208 213 216 224 247 250 253 258 265 274 288 304
320 339 498 542
根据以上数据,应当如何确定阶梯电价中的电量临界值,才能使得电价更为合理?
(计划实施3阶的阶梯电价,分布如下:75%用户在第一档(最低一档),20%用户在第二档,5%用户在第三档(最高一档).)
初试身手
解:
因为100×75% = 75,所以第一个临界值为有序样本中第75个数177和第76个数178的均值177.5,为了便于操作可以取值为178.
因为100×95% = 95,所以第二个临界值为有序样本中第95个数288和第96个数304的平均数,这个平均数为296.
由此确定了电量临界值,阶梯电价可以规定如下:
用户每月用电量不超过178kW·h,则按第一档电价标准缴费;
每月用电量(单位:kW·h)在区间(178,296]内,其中的178kW·h按第一档电价标准收费,超过178kW·h的部分按第二档电价标准收费;
每月用电量超过296kW·h,其中的178kW·h按第一档电价标准收费,296–178=118(kW·h)按第二档电价标准缴费,超过296kW·h的部分按第三档电价标准缴费.
课堂小结
1.第p百分数.
2.计算一组n个数据的第p百分位数的步骤.
一般地,一组数据的第p百分位数是这样一个值,它使得这组数据中至少有p%的数据小于或等于这个值,且至少有(100-p)%的数据大于或等于这个值.
第1步:按从小到大排列原始数据.
第2步:计算i=n×p%.
第3步:若i不是整数,而大于i的比邻整数为j,则第p百分位数为第j项数据;
若i是整数,则第p百分位数是第i项与第(i+1)项数据的平均数.
3.常用的百分位数.
①四分位数: , , .
②其它常用的百分位数:1%,5%,10%,80%,90%,95%,99%.
25%
50%
75%
作业布置
作业: P203 练习 第1,2,3题.
补充:
1.如图是胜利中学高一1000名学生英语听力测试的累积相对
次数分配折线图,若李玉的成绩在第60百分位数,则成绩
为( )分?
A.35分 B.60分 C.70分 D.85分
2.数据1,2,3,4,5,6的60%分位数为( )
A.3 B.3.5 C.3.6 D.4
尽情享受学习数学的快乐吧!
我们下节课再见!
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
第九章
9.2.2 总体百分位数的估计
人教A版(2019)
教学目标
学习目标 数学素养
1.正确理解第p百分位数的概念,掌握第p百分位数的求法. 1.数据分析素养.
2.能用样本估计整体百分位数. 2.数据分析素养和运算素养.
知新引入
前面我们用频率分布表、频率分布直方图描述了居民用户月均用水量的样本数据,通过对图表的观察与分析,得出了一些样本数据的频率分布规律,由此推测了该市全体居民用户月均用水量的分布情况,得出了“大部分居民用户的月均用水量集中在一个较低值区域”等推断. 接下来的问题是,如何利用这些信息,为政府决策服务呢?下面我们对此进行讨论.
如下数据为某市通过随机抽样获得的100户居民月均用水量按从小到大的顺序排列的一组数据(单位:t)
1.3 1.3 1.8 2.0 2.0 2.0 2.0 2.1 2.2 2.3 2.3 2.4 2.6 2.6 3.0 3.2 3.2 3.6 3.6 3.7 3.8 4.0 4.1 4.3 4.4 4.6 4.7 4.9 4.9 4.9 5.1 5.1 5.1 5.2 5.3 5.4 5.4 5.5 5.5 5.5 5.5 5.6 5.7 5.7 5.9 6.0 6.0 6.4 6.4 6.8 6.8 7.0 7.1 7.1 7.1 7.5 7.7 7.8 7.8 7.9 8.1 8.6 8.8 9.0 9.5 9.9 10.0 10.1 10.2 10.2 10.5 10.8 11.1 11.2 12.0 12.0 12.4 13.3 13.6 13.6 13.8 13.8 14.0 14.9 15.7 16.0 16.7 16.8 17.0 17.9 18.3 19.4 20.5 21.6 22.2 22.4 24.3 24.5 25.6 28.0
知新探究
问题1:如果该市政府希望使80%的居民用户生活用水费支出不受影响,根据9.2.1节中100户居民用户的月均用水量数据,你能给市政府提出该确定居民用户月均用水量标准的建议吗?
首先要明确以下问题:根据市政府的要求确定居民用户
月均用水量标准,就是寻找一个数a,使全市居民用户月用水量中不超过a的占80%,大于a的占20%.
你所在的地区是采用阶梯水价吗 标准是多少?
知新探究
下面我们通过样本数据对a的值进行估计.
1.3 1.3 1.8 2.0 2.0 2.0 2.0 2.1 2.2 2.3 2.3 2.4 2.6 2.6 3.0 3.2 3.2 3.6 3.6 3.7 3.8 4.0 4.1 4.3 4.4 4.6 4.7 4.9 4.9 4.9 5.1 5.1 5.1 5.2 5.3 5.4 5.4 5.5 5.5 5.5 5.5 5.6 5.7 5.7 5.9 6.0 6.0 6.4 6.4 6.8 6.8 7.0 7.1 7.1 7.1 7.5 7.7 7.8 7.8 7.9 8.1 8.6 8.8 9.0 9.5 9.9 10.0 10.1 10.2 10.2 10.5 10.8 11.1 11.2 12.0 12.0 12.4 13.3 13.6 13.6 13.8 13.8 14.0 14.9 15.7 16.0 16.7 16.8 17.0 17.9 18.3 19.4 20.5 21.6 22.2 22.4 24.3 24.5 25.6 28.0
把100样本数据按从小到大的顺序排列,得到第80个和第81个数据分别为13.6和13.8.可以发现,区间[13.6,13.8)内的任意一个数,都能把样本数据分成符合条件的两部分.一般地,我们取这两个数的平均数=13.7,并称此数为这组数据的第80百分位数(percentile),或80%分位数.
知新探究
根据样本数据的第80百分位数,我们可以估计总体数据的第80百分位数为13.7左右.由于样本的取值规律与总体的取值规律之间存在偏差,而在决策问题中,只要临界值近似为第80百分位数即可,因此为了实际中操作方便,可以建议市政府把月均用水量标准定为14.0t,或者把年用水量标准定为168t.
你认为14.0t这个标准一定能够保证80%居民不超标准吗?如果不一定,那么哪些环节可能会导致结论的差别
一般地,一组数据的第p百分位数是这样一个值,它使得这组数据中至少有p%的数据小于或等于这个值,且至少有(100-p)%的数据大于或等于这个值.
知新探究
一般地,一组数据的第p百分位数是这样一个值,它使得这组数据中至少有p%的数据小于或等于这个值,且至少有(100-p)%的数据大于或等于这个值.
可以通过下面的步骤计算一组n个数据的第p百分位数:
第1步:按从小到大排列原始数据.
第2步:计算i=n×p%.
第3步:若i不是整数,而大于i的比邻整数为j,则第p百分位数为第j项数据;
若i是整数,则第p百分位数是第i项与第(i+1)项数据的平均数.
对于任意一组数据,满足第p百分位数定义的值可能不唯一. 计算百分位数的方法有多种,我们取一种计算方法比较简单的.
知新探究
我们在初中学过的中位数,相当于第50百分位数.
在实际应用中,除了中位数外,常用的分位数还有第25百分位数,第75百分位数,这三个分位数把一组由小到大排列后的数据分成四等份,因此称为四分位数.
其中第25百分位数也称为第一四分位数或下四分位数等,第75百分位数也称为第三四分位数或上四分位数等.
另外,像第1百分位数,第5百分位数,第95百分位数和第99百分位数在统计中也经常被应用.
25%
第一四分位数
(下四分位数)
50%
75%
中位数
第三四分位数
(上四分位数)
知新探究
百分位数的特点
⑴第0百分位数是数据组中的最小数,第100百分位数是数据组中的最大数;
⑵一组数据的第p百分位数可能是这组数据中的数,也可能不是这组数据中的数;
⑶一组数据中的某些百分位数可能是同一个数.
知新探究
【例1】根据9.1.2节问题3树人中学高一年级女生的样本数据:
估计树人中学高一年级女生的第25,50,75百分位数.
163.0 164.0 161.0 157.0 162.0 165.0 158.0 155.0 164.0 162.5
154.0 154.0 164.0 149.0 159.0 151.0 170.0 171.0 155.0 148.0
172.0 162.5 158.0 155.5 157.0 163.0 172.0
解:
把27名女生的样本数据按从小到大排序,可得
148.0 149.0 154.0 154.0 155.0 155.0 155.5 157.0 157.0
158.0 158.0 159.0 161.0 161.0 162.0 162.5 162.5 163.0
163.0 164.0 164.0 164.0 165.0 170.0 171.0 172.0 172.0
由25%×27=6.75,50%×27=13.5,75%×27=20.25,
可知样本数据的第25,50,75百分位数为第7,14,21项数据,分别为155.5,161,164.
据此可以估计树人中学高一年级女生的第25,50,75百分位数分别约为155.5,161和164.
由于女生的样本量比较小,所以这里对总体的估计可能会存在比较大的误差.
知新探究
【例2】根据9.2.1表(下表)估计月均用水量的样本数据的80%和95%分位数.
解:
分组 频数 频率
[1.2,4.2) 23 0.23
[4.2,7.2) 32 0.32
[7.2,10.2) 13 0.13
[10.2,13.2) 9 0.09
[13.2,16.2) 9 0.09
[16.2,19.2) 5 0.05
[19.2,22.2) 3 0.03
[22.2,25.2) 4 0.04
[25.2,28.2) 2 0.02
合计 100 1.00
由表可知,月均用水量在13.2t以下的居民用户所占比例为
23%+32%+13%+9%=77%,
在16.2t以下的居民用户所占比例为
77%+9%=86%,
分析:在某些情况下,我们只能获得整理好的统计表或统计图,与原始数据相比,它们损失了一些信息,由表可知在[16.2,19.2)内有5个数据,但不知道这5个数据具体是多少.此时,通常把它们均匀地分布在此区间上.
知新探究
【例2】根据9.2.1表(下表)估计月均用水量的样本数据的80%和95%分位数.
分组 频数 频率
[1.2,4.2) 23 0.23
[4.2,7.2) 32 0.32
[7.2,10.2) 13 0.13
[10.2,13.2) 9 0.09
[13.2,16.2) 9 0.09
[16.2,19.2) 5 0.05
[19.2,22.2) 3 0.03
[22.2,25.2) 4 0.04
[25.2,28.2) 2 0.02
合计 100 1.00
月均用水量在13.2t以下的居民用户所占比例为
23%+32%+13%+9%=77%,
在16.2t以下的居民用户所占比例为
77%+9%=86%,
因此,80%分位数一定位于[13.2,16.2)内
由 13.2+3×=14.2.
可以估计月均用水量的样本数据的80%分位数约为14.2.
类似地,由 22.2+3×=22.95.
可以估计月均用水量的样本数据的95%分位数约为22.95.
知新探究
【例3】某经销商从外地一水殖厂购进一批小龙虾,并随机抽取40只进行统计,按重量分类统计结果如图:
⑴估计这批小龙虾重量的第10百分位数与第90百分位数.
⑵该经销商将这批小龙虾分成三个等级,如上表,则这批小龙虾划为几等品比较合理?
等级 三等品 二等品 一等品
重量(克) [5,25) [25,5) [45,55]
知新探究
解:
⑴因为40×10%=4,所以第10百分位数为第4项与第5项的平均数,
在[5,15)范围内约为=10,
因为40×90%=36,所以第90百分位数为第36项与第37项的平均数,
在[35,55]范围内,约为=45,
⑵由⑴知,将这批小龙虾重量集中在[10,45]范围内,所以划为二等品比较合理.
所以估计这批小龙虾重量的第10百分位数为10,第90百分位数为45.
初试身手
1.初三(2)班有学生42人,一次数学段考成绩如下:28、28、30、32、35、45、
56、56、58、60、61、61、62、64、64、66、76、76、78、80、80、84、86、87、
87、88、89、90、90、92、92、92、94、94、96、96、97、97、97、99、100、100.则第80百分位数是( )分
A.56 B.57 C.94 D.95
解:
由42×80%=33.6,所以取第34位为94分,则第80百分位数是94分.故选C.
C
初试身手
2.西安地铁2号线某机车某日10时从草滩站驶往安远门站的过程中,10个车站上车的人数统计如下:70,60,60,50,60,40,40,30,30,10,则这组数据的第25百分位数、第50百分位数的和为( )
A.90 B.75 C.70 D.65
解:
数据从大到小排列如下:70,60,60,60,50,40,40,30,30,10.
因为10×25%=2.5,按从小到大排列后,第25百分位数是第3项,即30;
第50百分位数即中位数是=45,
所以第25百分位数、第50百分位数的和为75.故选B.
B
初试身手
3.如图所示是一样本的频率分布直方图,样本数据共分3组,
分别为[5,10),[10,15),[15,20].估计样本数据的
第60百分位数是( )
A.14 B.15 C.16 D.17
解:
由频率分布直方图知,第1组的频率为0.04×5=0.2;
第2组的频率为0.10×5=0.5;
设样本数据的第60百分位数是x,
则0.2+0.10(x﹣10)=0.6,解得x=14,
所以估计样本数据的第60百分位数是14.
A
初试身手
4.为了实现绿色发展,避免浪费能源,某市政府计划对居民用电采用阶梯式收费的方法。为此,相关部门在该市随机调查了100户居民六月份的用电量(单位:kW·h),以了解这个城市家庭用电量的情况。数据如下:
8 22 42 49 51 57 60 61 62 63 65 67 70 71 72 76 77 78 80 82 83 84 88 90 93 94 96 96 98 98 100 100 101 105 106 107 107 108 109 110 110 112 113 115 118 120 121 124 127 130 130 131 132 133 134 134 135 135 137 138 139 141 144 146 148 151 154 159 162 163 165 169 170 174 177 178 182 187 191 192 194 201 202 203 208 213 216 224 247 250 253 258 265 274 288 304
320 339 498 542
根据以上数据,应当如何确定阶梯电价中的电量临界值,才能使得电价更为合理?
(计划实施3阶的阶梯电价,分布如下:75%用户在第一档(最低一档),20%用户在第二档,5%用户在第三档(最高一档).)
初试身手
解:
因为100×75% = 75,所以第一个临界值为有序样本中第75个数177和第76个数178的均值177.5,为了便于操作可以取值为178.
因为100×95% = 95,所以第二个临界值为有序样本中第95个数288和第96个数304的平均数,这个平均数为296.
由此确定了电量临界值,阶梯电价可以规定如下:
用户每月用电量不超过178kW·h,则按第一档电价标准缴费;
每月用电量(单位:kW·h)在区间(178,296]内,其中的178kW·h按第一档电价标准收费,超过178kW·h的部分按第二档电价标准收费;
每月用电量超过296kW·h,其中的178kW·h按第一档电价标准收费,296–178=118(kW·h)按第二档电价标准缴费,超过296kW·h的部分按第三档电价标准缴费.
课堂小结
1.第p百分数.
2.计算一组n个数据的第p百分位数的步骤.
一般地,一组数据的第p百分位数是这样一个值,它使得这组数据中至少有p%的数据小于或等于这个值,且至少有(100-p)%的数据大于或等于这个值.
第1步:按从小到大排列原始数据.
第2步:计算i=n×p%.
第3步:若i不是整数,而大于i的比邻整数为j,则第p百分位数为第j项数据;
若i是整数,则第p百分位数是第i项与第(i+1)项数据的平均数.
3.常用的百分位数.
①四分位数: , , .
②其它常用的百分位数:1%,5%,10%,80%,90%,95%,99%.
25%
50%
75%
作业布置
作业: P203 练习 第1,2,3题.
补充:
1.如图是胜利中学高一1000名学生英语听力测试的累积相对
次数分配折线图,若李玉的成绩在第60百分位数,则成绩
为( )分?
A.35分 B.60分 C.70分 D.85分
2.数据1,2,3,4,5,6的60%分位数为( )
A.3 B.3.5 C.3.6 D.4
尽情享受学习数学的快乐吧!
我们下节课再见!
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
