小初衔接暑假专题1-几何初步知识
图片预览




文档简介
暑期专题辅导材料一
【教学内容】
小升初衔接课程——几何初步知识
【教学目的】
1、掌握直线、射线、线段三者之间的联系和区别;能熟练地辨别垂线与平行线以及常见的几种角;会画已知直线的平行线与垂线。
2、掌握长方形、正方形、平行四边行、三角形、梯形、圆、长方体、正方体、圆柱、圆锥的主要特征;会画长方形、正方形、圆;进一步认识轴对称图形与对称轴。
3、加深对平面图形的周长、面积、体积意义的理解;通过公式的推导,加深对辩证唯物主义事物都是联系的观点,使学生能熟练掌握已学过平面图形的周长、面积、立体图形的表面积体积公式计算,并能应用公式来解答一些实际问题。
【知识讲解】
1、平面图形的认识
(1)点——直线——线段——射线
用直尺把两点连接起来,就得到一条线段,把线段的一端无限延长,可以得到一条射线;把线段的两端无限延长,可以得到一条直线。
(2)直线、射线和线段有什么联系和区别?
名 称 图 形 特 征 备 注
直 线 没有端点,可以无限延长 不可以度量
射 线 有一个端点,可以向一端无限延长 不可以度量
线 段 有两个端点,长度是有限的 可以度量
(3)同一平面里两条直线的位置关系。
平行 —— 平行线
锐角(小于90°)
两 直角 —— 互相垂直 —— 垂线
条 (等于90°)
直 相交 —— 角 钝角(大于90°小于180°)
线 平角(等于180°)
周角(等于360°)
重合
(4)①角的大小要看两条边叉开的大小,叉开得越大,角越大。角的大小与角的两边画的长短没有关系。
②两条直线相交成直角时,这两条直线互相垂直。
③在同一个平面内,不相交的两条直线叫做平行线,也可以说是互相平行。
锐角三角形
按角分 直角三角形
①三角形 钝角三角形
(内角和是180°) 不等边三角形
平 按边分 等腰三角形
等边三角形
面 不规则四边形
图 平行四边形 长方形 正方形
②四边形
形 (内角和是360°)
等腰梯形
梯形
直角梯形
③圆、扇形……
(6)在同圆、等圆里,所有的直径都相等,所有的半径也相等,直径等于半径的2倍,直径所在的直线是对称轴。周长和直径的比,(比值一定)叫做圆周率,用字母表示。圆心确定圆的位置,半径确定圆的大小。
(7)①如果一个图形沿着一条直线对折,两侧的图形能够完全重合,这个图形叫做轴对称图形,这条直线叫做对称轴。
②学过的轴对称图形有:长方形(2条对称轴)、正方形(4条对称轴)、等边三角形(3条对称轴)、等腰三角形(1条对称轴)、等腰直角三角形(1条对称轴)、等腰梯形(1条对称轴)、圆(无数条对称轴)、扇形(1条对称轴)。
2、平面图形的周长和面积
(1)围成一个图形的所有边长的总和叫做这个图形的周长。
(2)物体的表面或围成的平面图形的大小,叫做它们的面积。
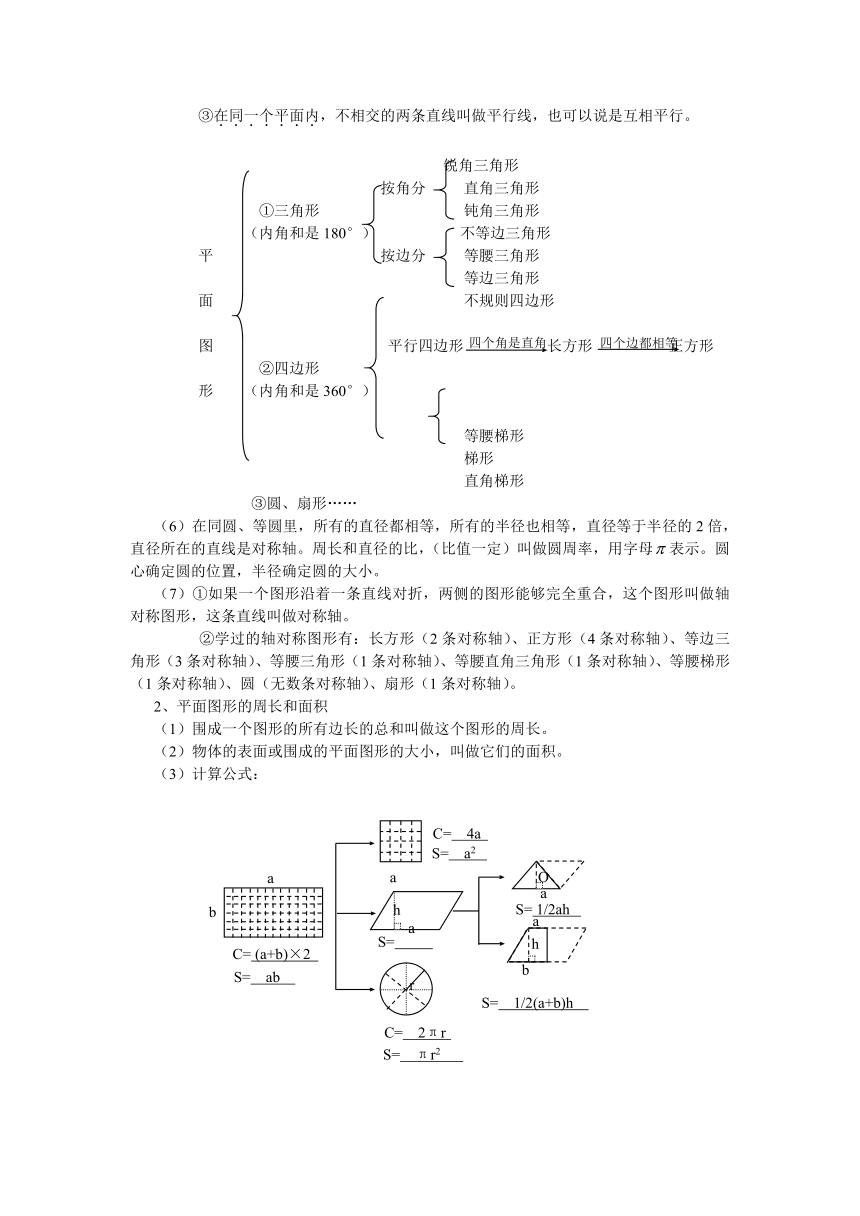
(3)计算公式:
(4)这些公式的推导过程:
以梯形面积公式为例,把两个完全一样的梯形(如正面右下图所示)拼成一个平行四边形;可以看出这个平行四边形的底等于梯形上底加下底的和,高等于原来梯形的高;每个梯形的面积等于拼成的平行四边形面积的一半,所以梯形的面积=(上底+下底)×高÷2=。
3、立体图形的表面积和体积
(1)一个立体图形所有的面的面积总和,叫做它的表面积。
(2)一个立体图形所占空间的大小叫做它的体积。
(3)长方体和正方体的特征:
形体 相 同 点 不 同 点 关 系
面 棱 点 面 的 形 状 面 积 棱 长
长方体 6个 12条 8个 6个面都是长方形(也可能有两个相对的面的正方形) 相对的面的面积相等 每一组互相平行的四条棱的长度相等。 正方体是特殊的长方体
正方体 6个 12条 8个 6个面都是相等的正方形 6个面的面积都相等 12条棱的长度都相等。
(4)圆柱和圆锥的特征:
名 称 基 本 特 征
直 圆 柱 1、上、下两个底面是面积相等的圆。2、两个底面之间的距离叫高,高垂直于上、下两个底面。3、圆柱的侧面展形是个长方形。(长=底面周长,宽=高)
直 圆 锥 1、底面是一个圆。2、从顶点到底面圆心的距离叫高,高垂直于底面圆。3、圆锥的体积等于和它等底、等高的圆柱体积的三分之一。
(5)计算公式:
【典型例题】
例1、下面几个图形中,哪些是直线?哪些是线段?哪些是射线?
分析:直线、线段、射线首先必须是“直”的,不能有弯折。而判定一条“直”的线属于哪一种类型,依据就是端点的个数,如果没有端点,那么它就是直线;有一个端点,就是射线;有两个端点,它就是线段。
答:(3)是直线,(2)是射线,(5)是线段。
例2、求下图中角的度数。
∠1 = 度
∠2 = 度
∠3 = 度
解:先求出∠1的度数。(180°-150°=30°)
再求出∠2的度数。(180°-30°-32°=118°)
最后求出∠3的度数。(180°-118°=62°)
例3、判断下列各题,正确的打“√”错的“×”。
(1)直线AB长3厘米。………………………………………( )
(2)角越大,角的边越大。……………………………………( )
(3)不相交的两条直线叫平行线。……………………………( )
(4)平行线间距离处处相等。…………………………………( )
(5)黑板的边是垂线。…………………………………………( )
分析与解:
(1)因为直线是向两端无限延伸着的,它没有端点,所以无法度量。所以,原题是错的。
(2)因为角的大小与边的长短无关,与角两边叉开大小有关。所以原题是错的。
(3)因为原题没有强调“在同一平面内”这个前提,所以原题是错的。
(4)此题是正确的。
(5)因为垂直是指两条直线的相互位置关系,不能孤立地说某一条线是垂线。应该说“黑板的长边是短边的垂线”。所以原题是错的。
例4、求右图的周长。(单位:分米)
解:下图的周长包括长方形的两条长,一条宽与半圆弧长的总和。
例5、已知梯形面积是12平方厘米,求阴影部分的面积。
解法一:阴影部分是一个三角形,它的底是3厘米,要求它的面积,还需知道高,根据梯形面积的计算公式不难求出高。
解法二:因为阴影部分与空白部分是两个等高的三角形,所以它们面积的比就是它们底边长的比,即3:5。由此可知,阴影部分的面积相当于梯形面积的,阴影部分的面积可以直接求出。
(平方厘米)
例6、有一块长方形土地,长100米,宽是长的,把这块地划出一个最大的正方形地种小麦,每公顷平均产小麦6吨。把全部小麦的磨成面粉,小麦的出粉率是81%,可磨出面粉多少千克?(得数保留整千克。)
分析:先求出长方形地的宽,即正方形小麦地的边长;进而求出正方形小麦地的面积,然后可以求出全部小麦的重量;再求出全部小麦的是多少千克,最后求出这些小麦可以磨出面粉多少千克。
解:(1)正方形小麦地的边长:(米)
(2)正方形小麦地的面积:(平方米)
3600平方米 = 0.36公顷
(3)全部小麦的重量:
(4)磨面粉的小麦重是:(千克)
(5)磨出面粉的重量:
(千克)
答:约可磨出面粉350千克。
例7、有一个近似于圆锥的稻谷堆,底面周长是18.84米,高1.5米,把它装入一个底面积是7.8平方米的圆柱形粮囤正好装满,这个粮囤的高多少米?(保留一位小数)
分析:把一个圆锥形的稻谷堆装入一个圆柱形的粮囤里正好装满,说明圆锥的体积正好等于圆柱的容积。
解:
答:这个粮囤高约1.8米。
【跟踪练习】
一、判断题:(正确的打“√”,错的打“×”)
1、不相交的两条直线叫平行线。 ( )
2、两个长方形周长相等,它们的面积必定相等。 ( )
3、有一个角是锐角的三角形叫做锐角三角形。 ( )
4、正方形的边长扩大3倍,它的面积就扩大6倍。 ( )
5、半径是直径的一半,直径是半径的2倍。 ( )
6、一个圆的周长与半径成正比例关系。 ( )
7、扇形是轴对称图形,有无数条对称轴。 ( )
8、决定圆锥体积大小的条件是底面半径和圆锥的高。 ( )
9、一个棱长6分米的正方体,它的表面积与体积相等。 ( )
10、等底等高的圆柱和圆锥,圆柱的体积比圆锥大2倍。 ( )
二、填空题
11、等腰三角形的顶角与一个底角的和是135°,它的顶角是( )度。
12、一个正方形周长是0.4米,面积是( )平方米。
13、一块平行四边形的面积是264平方米,它的高是12米,底是( )。
14、一个圆的周长是6.28厘米,它的面积是( )。
15、一个正方体的棱长是2厘米,它的表面积是( ),体积是( )。
16、两个棱长1分米的正方体木块,拼成一个长方体,这个长方体的表面积是( )。
17、一个圆柱的底面直径和高都是10厘米,它的侧面积是( ),表面积是( ),体积是( )。
18、一个圆锥和一个圆柱的底面积、体积都相等,如果圆锥的高是54厘米,圆柱的高是( )。
19、如右图, ∠1 = ( )°
∠2 = ( )°
∠3 = ( )°
20、一个正方形,一边截去6厘米,另一边截去2厘米,剩下的长方形面积比原正方形面积少68平方厘米。原正方形的边长是( )。
三、求下面各图形的阴影部分的周长和面积。(单位:厘米)
21、 22、 23、
四、求下面几何图形的体积。(单位:厘米)
24、 25、
五、应用题:
26、一个长方形地,周长是50米,长是宽的1.5倍,这块地的面积是多少平方米?
27、要制作一对圆柱形无盖铁皮水桶,底面周长是12.56分米,高是6分米,至少要用铁皮多少平方分米?(得数保留整数)
28、有一个圆形鱼池,直径13米,紧沿着池边修一条宽2米的小道,小道面积是多少?
29、一个圆锥形的碎石堆,底面半径1.8米,高1.5米。如果每立方米碎石重2.2吨,这堆碎石大约重多少吨?(得数保留整吨数)
30、一个圆柱和一个圆锥等底等高,体积相差3.6立方分米,这个圆柱的体积是多少立方分米?
31、用3个相同的正方体,粘接成一个长方体,长方体的棱长总和是40分米,这个长方体的表面积与体积各是多少?
32、水结成冰时,冰的体积比水增加。把一块长8分米,宽5分米,厚1.2分米的冰溶化在一只底面为8平方分米的圆柱形储水桶里,桶里水高与桶高的比为4:5,求圆柱形储水桶的高。
参考答案与提示
一、判断题:
1、× 2、× 3、× 4、× 5、×
6、√ 7、× 8、√ 9、× 10、√
二、填空题:
11、45 12、0.01
13、22米 14、3.14平方厘米
15、24平方厘米、8立方厘米
16、10平方分米
17、314平方厘米、471平方厘米、785立方厘米
18、18厘米
19、90°、50°、180° 20、10厘米
三、21、C = 6.28厘米,S = 0.86平方厘米
22、C = 18.84厘米,S = 6.28平方厘米
23、C = 28.56厘米,S = 19.44平方厘米
四、24、94.2立方厘米
25、3.6立方厘米
五、应用题:
26、(米)…… 宽
(米)……………… 长
(平方米)………… 面积
27、(分米)…… 底面半径
28、(米)……………………… 内圆半径
6.5 + 2 = 8.5(米)…………………… 外圆半径
(平方米)………… 环形面积
29、(立方米)……… 圆锥形石堆的体积
吨(吨)
30、(立方分米)
31、(分米)…………………… 正方体的棱长
(平方分米)………………………… 表面积
(立方分米)…………………………… 体积
32、(立方分米)………………………… 冰的体积
(立方分米)……………………… 水的体积
(分米)…………………………………… 水的高
(分米)…………………………… 桶的高
四个角是直角
四个边都相等
C= 4a
S= a2
C= (a+b)×2
S= ab
a
b
a
h
a
S=
a
b
h
S= 1/2(a+b)h
S= 1/2ah
a
r
C= 2πr
S= πr2
O1
(1)
(2)
(3)
(4)
(5)
1
2
3
32°
150°
40
20
3
5
40°
2
1
3
O1
O
O2
2
4
4
8
O
O1
O2
O3
2
1.5
0.8
6
6
3
1
PAGE
【教学内容】
小升初衔接课程——几何初步知识
【教学目的】
1、掌握直线、射线、线段三者之间的联系和区别;能熟练地辨别垂线与平行线以及常见的几种角;会画已知直线的平行线与垂线。
2、掌握长方形、正方形、平行四边行、三角形、梯形、圆、长方体、正方体、圆柱、圆锥的主要特征;会画长方形、正方形、圆;进一步认识轴对称图形与对称轴。
3、加深对平面图形的周长、面积、体积意义的理解;通过公式的推导,加深对辩证唯物主义事物都是联系的观点,使学生能熟练掌握已学过平面图形的周长、面积、立体图形的表面积体积公式计算,并能应用公式来解答一些实际问题。
【知识讲解】
1、平面图形的认识
(1)点——直线——线段——射线
用直尺把两点连接起来,就得到一条线段,把线段的一端无限延长,可以得到一条射线;把线段的两端无限延长,可以得到一条直线。
(2)直线、射线和线段有什么联系和区别?
名 称 图 形 特 征 备 注
直 线 没有端点,可以无限延长 不可以度量
射 线 有一个端点,可以向一端无限延长 不可以度量
线 段 有两个端点,长度是有限的 可以度量
(3)同一平面里两条直线的位置关系。
平行 —— 平行线
锐角(小于90°)
两 直角 —— 互相垂直 —— 垂线
条 (等于90°)
直 相交 —— 角 钝角(大于90°小于180°)
线 平角(等于180°)
周角(等于360°)
重合
(4)①角的大小要看两条边叉开的大小,叉开得越大,角越大。角的大小与角的两边画的长短没有关系。
②两条直线相交成直角时,这两条直线互相垂直。
③在同一个平面内,不相交的两条直线叫做平行线,也可以说是互相平行。
锐角三角形
按角分 直角三角形
①三角形 钝角三角形
(内角和是180°) 不等边三角形
平 按边分 等腰三角形
等边三角形
面 不规则四边形
图 平行四边形 长方形 正方形
②四边形
形 (内角和是360°)
等腰梯形
梯形
直角梯形
③圆、扇形……
(6)在同圆、等圆里,所有的直径都相等,所有的半径也相等,直径等于半径的2倍,直径所在的直线是对称轴。周长和直径的比,(比值一定)叫做圆周率,用字母表示。圆心确定圆的位置,半径确定圆的大小。
(7)①如果一个图形沿着一条直线对折,两侧的图形能够完全重合,这个图形叫做轴对称图形,这条直线叫做对称轴。
②学过的轴对称图形有:长方形(2条对称轴)、正方形(4条对称轴)、等边三角形(3条对称轴)、等腰三角形(1条对称轴)、等腰直角三角形(1条对称轴)、等腰梯形(1条对称轴)、圆(无数条对称轴)、扇形(1条对称轴)。
2、平面图形的周长和面积
(1)围成一个图形的所有边长的总和叫做这个图形的周长。
(2)物体的表面或围成的平面图形的大小,叫做它们的面积。
(3)计算公式:
(4)这些公式的推导过程:
以梯形面积公式为例,把两个完全一样的梯形(如正面右下图所示)拼成一个平行四边形;可以看出这个平行四边形的底等于梯形上底加下底的和,高等于原来梯形的高;每个梯形的面积等于拼成的平行四边形面积的一半,所以梯形的面积=(上底+下底)×高÷2=。
3、立体图形的表面积和体积
(1)一个立体图形所有的面的面积总和,叫做它的表面积。
(2)一个立体图形所占空间的大小叫做它的体积。
(3)长方体和正方体的特征:
形体 相 同 点 不 同 点 关 系
面 棱 点 面 的 形 状 面 积 棱 长
长方体 6个 12条 8个 6个面都是长方形(也可能有两个相对的面的正方形) 相对的面的面积相等 每一组互相平行的四条棱的长度相等。 正方体是特殊的长方体
正方体 6个 12条 8个 6个面都是相等的正方形 6个面的面积都相等 12条棱的长度都相等。
(4)圆柱和圆锥的特征:
名 称 基 本 特 征
直 圆 柱 1、上、下两个底面是面积相等的圆。2、两个底面之间的距离叫高,高垂直于上、下两个底面。3、圆柱的侧面展形是个长方形。(长=底面周长,宽=高)
直 圆 锥 1、底面是一个圆。2、从顶点到底面圆心的距离叫高,高垂直于底面圆。3、圆锥的体积等于和它等底、等高的圆柱体积的三分之一。
(5)计算公式:
【典型例题】
例1、下面几个图形中,哪些是直线?哪些是线段?哪些是射线?
分析:直线、线段、射线首先必须是“直”的,不能有弯折。而判定一条“直”的线属于哪一种类型,依据就是端点的个数,如果没有端点,那么它就是直线;有一个端点,就是射线;有两个端点,它就是线段。
答:(3)是直线,(2)是射线,(5)是线段。
例2、求下图中角的度数。
∠1 = 度
∠2 = 度
∠3 = 度
解:先求出∠1的度数。(180°-150°=30°)
再求出∠2的度数。(180°-30°-32°=118°)
最后求出∠3的度数。(180°-118°=62°)
例3、判断下列各题,正确的打“√”错的“×”。
(1)直线AB长3厘米。………………………………………( )
(2)角越大,角的边越大。……………………………………( )
(3)不相交的两条直线叫平行线。……………………………( )
(4)平行线间距离处处相等。…………………………………( )
(5)黑板的边是垂线。…………………………………………( )
分析与解:
(1)因为直线是向两端无限延伸着的,它没有端点,所以无法度量。所以,原题是错的。
(2)因为角的大小与边的长短无关,与角两边叉开大小有关。所以原题是错的。
(3)因为原题没有强调“在同一平面内”这个前提,所以原题是错的。
(4)此题是正确的。
(5)因为垂直是指两条直线的相互位置关系,不能孤立地说某一条线是垂线。应该说“黑板的长边是短边的垂线”。所以原题是错的。
例4、求右图的周长。(单位:分米)
解:下图的周长包括长方形的两条长,一条宽与半圆弧长的总和。
例5、已知梯形面积是12平方厘米,求阴影部分的面积。
解法一:阴影部分是一个三角形,它的底是3厘米,要求它的面积,还需知道高,根据梯形面积的计算公式不难求出高。
解法二:因为阴影部分与空白部分是两个等高的三角形,所以它们面积的比就是它们底边长的比,即3:5。由此可知,阴影部分的面积相当于梯形面积的,阴影部分的面积可以直接求出。
(平方厘米)
例6、有一块长方形土地,长100米,宽是长的,把这块地划出一个最大的正方形地种小麦,每公顷平均产小麦6吨。把全部小麦的磨成面粉,小麦的出粉率是81%,可磨出面粉多少千克?(得数保留整千克。)
分析:先求出长方形地的宽,即正方形小麦地的边长;进而求出正方形小麦地的面积,然后可以求出全部小麦的重量;再求出全部小麦的是多少千克,最后求出这些小麦可以磨出面粉多少千克。
解:(1)正方形小麦地的边长:(米)
(2)正方形小麦地的面积:(平方米)
3600平方米 = 0.36公顷
(3)全部小麦的重量:
(4)磨面粉的小麦重是:(千克)
(5)磨出面粉的重量:
(千克)
答:约可磨出面粉350千克。
例7、有一个近似于圆锥的稻谷堆,底面周长是18.84米,高1.5米,把它装入一个底面积是7.8平方米的圆柱形粮囤正好装满,这个粮囤的高多少米?(保留一位小数)
分析:把一个圆锥形的稻谷堆装入一个圆柱形的粮囤里正好装满,说明圆锥的体积正好等于圆柱的容积。
解:
答:这个粮囤高约1.8米。
【跟踪练习】
一、判断题:(正确的打“√”,错的打“×”)
1、不相交的两条直线叫平行线。 ( )
2、两个长方形周长相等,它们的面积必定相等。 ( )
3、有一个角是锐角的三角形叫做锐角三角形。 ( )
4、正方形的边长扩大3倍,它的面积就扩大6倍。 ( )
5、半径是直径的一半,直径是半径的2倍。 ( )
6、一个圆的周长与半径成正比例关系。 ( )
7、扇形是轴对称图形,有无数条对称轴。 ( )
8、决定圆锥体积大小的条件是底面半径和圆锥的高。 ( )
9、一个棱长6分米的正方体,它的表面积与体积相等。 ( )
10、等底等高的圆柱和圆锥,圆柱的体积比圆锥大2倍。 ( )
二、填空题
11、等腰三角形的顶角与一个底角的和是135°,它的顶角是( )度。
12、一个正方形周长是0.4米,面积是( )平方米。
13、一块平行四边形的面积是264平方米,它的高是12米,底是( )。
14、一个圆的周长是6.28厘米,它的面积是( )。
15、一个正方体的棱长是2厘米,它的表面积是( ),体积是( )。
16、两个棱长1分米的正方体木块,拼成一个长方体,这个长方体的表面积是( )。
17、一个圆柱的底面直径和高都是10厘米,它的侧面积是( ),表面积是( ),体积是( )。
18、一个圆锥和一个圆柱的底面积、体积都相等,如果圆锥的高是54厘米,圆柱的高是( )。
19、如右图, ∠1 = ( )°
∠2 = ( )°
∠3 = ( )°
20、一个正方形,一边截去6厘米,另一边截去2厘米,剩下的长方形面积比原正方形面积少68平方厘米。原正方形的边长是( )。
三、求下面各图形的阴影部分的周长和面积。(单位:厘米)
21、 22、 23、
四、求下面几何图形的体积。(单位:厘米)
24、 25、
五、应用题:
26、一个长方形地,周长是50米,长是宽的1.5倍,这块地的面积是多少平方米?
27、要制作一对圆柱形无盖铁皮水桶,底面周长是12.56分米,高是6分米,至少要用铁皮多少平方分米?(得数保留整数)
28、有一个圆形鱼池,直径13米,紧沿着池边修一条宽2米的小道,小道面积是多少?
29、一个圆锥形的碎石堆,底面半径1.8米,高1.5米。如果每立方米碎石重2.2吨,这堆碎石大约重多少吨?(得数保留整吨数)
30、一个圆柱和一个圆锥等底等高,体积相差3.6立方分米,这个圆柱的体积是多少立方分米?
31、用3个相同的正方体,粘接成一个长方体,长方体的棱长总和是40分米,这个长方体的表面积与体积各是多少?
32、水结成冰时,冰的体积比水增加。把一块长8分米,宽5分米,厚1.2分米的冰溶化在一只底面为8平方分米的圆柱形储水桶里,桶里水高与桶高的比为4:5,求圆柱形储水桶的高。
参考答案与提示
一、判断题:
1、× 2、× 3、× 4、× 5、×
6、√ 7、× 8、√ 9、× 10、√
二、填空题:
11、45 12、0.01
13、22米 14、3.14平方厘米
15、24平方厘米、8立方厘米
16、10平方分米
17、314平方厘米、471平方厘米、785立方厘米
18、18厘米
19、90°、50°、180° 20、10厘米
三、21、C = 6.28厘米,S = 0.86平方厘米
22、C = 18.84厘米,S = 6.28平方厘米
23、C = 28.56厘米,S = 19.44平方厘米
四、24、94.2立方厘米
25、3.6立方厘米
五、应用题:
26、(米)…… 宽
(米)……………… 长
(平方米)………… 面积
27、(分米)…… 底面半径
28、(米)……………………… 内圆半径
6.5 + 2 = 8.5(米)…………………… 外圆半径
(平方米)………… 环形面积
29、(立方米)……… 圆锥形石堆的体积
吨(吨)
30、(立方分米)
31、(分米)…………………… 正方体的棱长
(平方分米)………………………… 表面积
(立方分米)…………………………… 体积
32、(立方分米)………………………… 冰的体积
(立方分米)……………………… 水的体积
(分米)…………………………………… 水的高
(分米)…………………………… 桶的高
四个角是直角
四个边都相等
C= 4a
S= a2
C= (a+b)×2
S= ab
a
b
a
h
a
S=
a
b
h
S= 1/2(a+b)h
S= 1/2ah
a
r
C= 2πr
S= πr2
O1
(1)
(2)
(3)
(4)
(5)
1
2
3
32°
150°
40
20
3
5
40°
2
1
3
O1
O
O2
2
4
4
8
O
O1
O2
O3
2
1.5
0.8
6
6
3
1
PAGE
同课章节目录
