5.3平行线的性质 同步练习(含解析)人教版数学七年级下册
文档属性
| 名称 | 5.3平行线的性质 同步练习(含解析)人教版数学七年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 631.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-03 00:00:00 | ||
图片预览



文档简介
5.3平行线的性质
(共25题,满分100分)
题号 一 二 三 总分
得分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.注意保持试卷整洁
一、单选题
1.如图,直线被直线所截,,,则的度数为( )
A. B. C. D.
2.如图,Rt△ABC中,∠ACB=90°,DE过点C且平行于AB,若∠BCE=35°,则∠A的度数为( )
A. B. C. D.
3.如图,桌面上有木条b固定,木条a在桌面上绕点O旋转n°(0<n<90)后与b平行,则n=( )
A.20 B.30 C.70 D.80
4.下列各命题的逆命题成立的是( )
A.对顶角相等 B.如果两个数相等,那么它们的绝对值相等
C.两直线平行,同位角相等 D.如果两个角都是,那么这两个角相等
5.如图,∠AOB的一边OA为平面镜,∠AOB=37°36′,在OB上有一点E,从E点射出一束光线经OA上一点D反射,反射光线DC恰好与OB平行,则∠DEB的度数是( )
A.74°12′ B.74°36′ C.75°12′ D.75°36′
6.用反证法证明某个命题的结论“”时,第一步应假设( )
A. B. C. D.
7.如图,一束光线与水平面成 的角度照射地面,现在地面AB上支放一个平面镜CD,使这束光线经过平面镜反射后成水平光线,则平面镜CD与地面AB所成角∠DCB的度数等于( )
A. B.45° C.50° D.60°
8.有下列四个命题:
①、同位角相等;②、如果两个角的和是 180 度,那么这两个角是邻补角;
③、在同一平面内,平行于同一条直线的两条直线互相平行;
④、在同一平面内,垂直于同一条直线的两条直线互相垂直. 其中是真命题的个数有( )个
A.0 B.1 C.2 D.3
9.下列是假命题的是( ).
A.直角都相等 B.同角的余角相等
C.相等的角是对顶角 D.过直线外一点,有且只有一条直线与已知直线平行
10.将一个直角三角板和一把直尺如图放置,如果∠a=44°,则∠β的度数是( )
A.43° B.44° C.45° D.46°
二、填空题
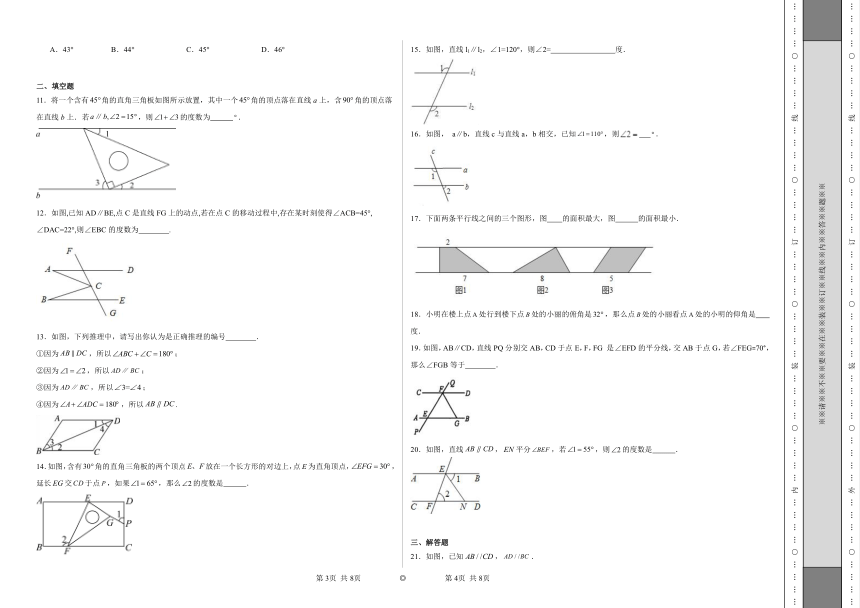
11.将一个含有角的直角三角板如图所示放置,其中一个角的顶点落在直线a上,含角的顶点落在直线b上.若,则的度数为 .
12.如图,已知AD∥BE,点C是直线FG上的动点,若在点C的移动过程中,存在某时刻使得∠ACB=45°, ∠DAC=22°,则∠EBC的度数为 .
13.如图,下列推理中,请写出你认为是正确推理的编号 .
①因为,所以;
②因为,所以;
③因为,所以;
④因为,所以.
14.如图,含有角的直角三角板的两个顶点放在一个长方形的对边上,点为直角顶点,,延长交于点,如果,那么的度数是 .
15.如图,直线l1∥l2,∠1=120°,则∠2= 度.
16.如图, a∥b,直线c与直线a,b相交,已知,则 .
17.下面两条平行线之间的三个图形,图 的面积最大,图 的面积最小.
18.小明在楼上点处行到楼下点处的小丽的俯角是,那么点处的小丽看点处的小明的仰角是 度.
19.如图,AB∥CD,直线PQ分别交AB,CD于点E,F,FG是∠EFD的平分线,交AB于点G,若∠FEG=70°,那么∠FGB等于 .
20.如图,直线,平分,若,则的度数是 .
三、解答题
21.如图,已知,.
(1)求证:;
(2)连结,若的2倍与的互余,比的2倍多,求和的度数.
22.如图,已知于点A,AE∥CD交于点E,且于点F.
求证:.
证明:∵于点A,于点F,(已知)
∴.(垂直的定义)
∴AD∥EF,( )
∴__________( )
∵AE∥CD,(已知)
∴________.(两直线平行,同位角相等)
∵,
∴.(等量代换)
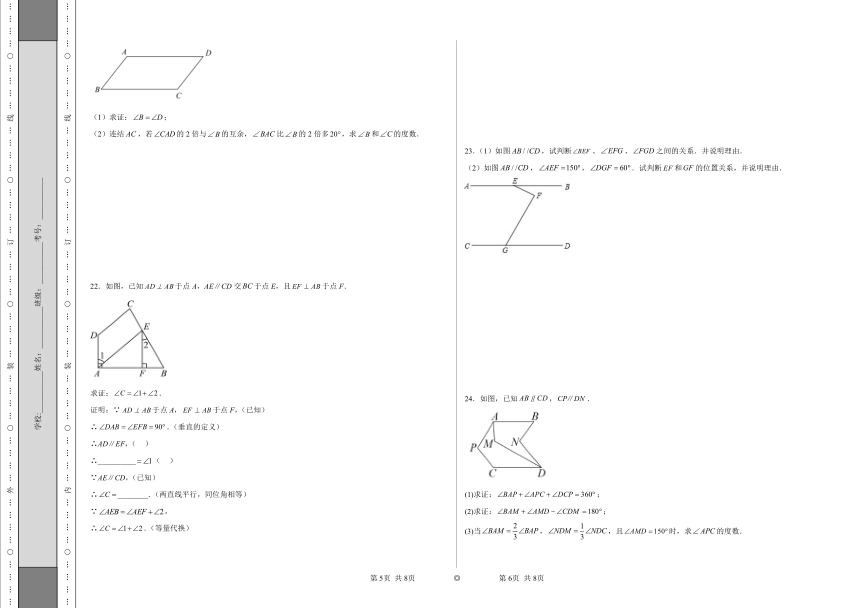
23.(1)如图,试判断、、之间的关系.并说明理由.
(2)如图,,.试判断和的位置关系,并说明理由.
24.如图,已知,.
(1)求证:;
(2)求证:;
(3)当,,且时,求的度数.
25.如图,,点E、F分别在线段、上,连结交于G,.若,,,求和的度数.
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
) (
学校:___________姓名:___________班级:___________考号:___________
) (
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
第1页 共4页 ◎ 第2页 共4页
第1页 共4页 ◎ 第2页 共4页
参考答案:
1.B
【分析】根据“两直线平行,内错角相等”和“邻补角互补”来求∠2的度数.
【详解】解:,
,
故选择:B
【点睛】本题考查了平行线的性质.平行线性质定理:定理1:两条平行线被第三条直线所截,同位角相等. 简单说成:两直线平行,同位角相等.定理2:两条平行线被地三条直线所截,同旁内角互补.简单说成:两直线平行,同旁内角互补.定理3:两条平行线被第三条直线所截,内错角相等. 简单说成:两直线平行,内错角相等.
2.C
【详解】分析:题中有三个条件,图形为常见图形,可先由AB∥DE,∠BCE=35°,根据两直线平行,内错角相等求出∠B,然后根据三角形内角和为180°求出∠A.
详解:∵AB∥DE,∠BCE=35°,∴∠B=∠BCE=35°(两直线平行,内错角相等).
又∵∠ACB=90°,∴∠A=90°﹣35°=55°(在直角三角形中,两个锐角互余).
故选C.
点睛:看到两直线平行时,应该想到它们的性质,由两直线平行的关系得到角之间的数量关系,从而达到解决问题的目的.
3.B
【详解】如图当a逆时针旋转至c位置时与b平行,旋转角为∠3,
∵c∥b,∴∠2=∠1=70°,
∵∠1+∠3=100°,∴∠3=30°.
∴n=30.
故选B.
点睛:本题关键在于结合旋转与平行线的性质解题,并且要注意旋转角的范围.
4.C
【分析】分别写出下列命题的逆命题,然后判断真假即可.
【详解】解:A.逆命题为相等的两个角是对顶角,逆命题不成立,不符合题意;
B.逆命题为两个数的绝对值相等,那么这两个相等,逆命题不成立,不符合题意;
C.逆命题是同位角相等,两直线平行,逆命题成立,符合题意;
D.逆命题为两个角相等,那么两个角都是,逆命题不成立,不符合题意.
故选:C.
【点睛】本题考查命题与定理的知识,解题的关键是能够写出该命题的逆命题并作出正确的判断.
5.C
【详解】试题分析:过点D作DF⊥AO交OB于点F.∵入射角等于反射角,∴∠1=∠3,∵CD∥OB,∴∠1=∠2(两直线平行,内错角相等);∴∠2=∠3(等量代换);在Rt△DOF中,∠ODF=90°,∠AOB=37°36′,∴∠2=90°﹣37°36′=52°24′;∴在△DEF中,∠DEB=180°﹣2∠2=75°12′.故选C.
考点:1.平行线的性质;2.度分秒的换算;3.跨学科.
6.D
【分析】根据反证法的步骤可直接进行排除选项.
【详解】解:用反证法证明某个命题的结论“”时,第一步应假设;
故选D.
【点睛】本题主要考查反证法,熟练掌握反证法是解题的关键.
7.A
【详解】
∵入射角等于反射角,
∴∠1=∠2,
∵光线经过平面镜CD反射后成水平光线平行,
∴∠2=∠4,
又∵∠1=∠3(对顶角相等),
∴∠3=∠4,
∴∠2=∠3,
∵光线与水平面成60°的角度照射地面,
∴∠3=60°÷2=30°,
∴∠4=30°,即∠DCB=30°
故选A
8.B
【分析】根据同位角的性质、补角的定义、垂直和平行的性质求解即可.
【详解】①、两直线平行,同位角相等,错误;
②、如果两个角的和是 180 度,那么这两个角是补角,错误;
③、在同一平面内,平行于同一条直线的两条直线互相平行,正确;
④、在同一平面内,垂直于同一条直线的两条直线互相平行,错误.
其中是真命题的有1个
故答案为:B.
【点睛】本题考查了,掌握同位角的性质、补角的定义、垂直和平行的性质是解题的关键.
9.C
【分析】根据直角、余角的概念、对顶角的概念、平行线的判定进行判断.
【详解】A、直角都相等,是真命题;
B、同角的余角相等,是真命题;
C、相等的角不一定是对顶角,则相等的角是对顶角是假命题;
D、过直线外一点有且只有一条直线与这条直线平行,是真命题;
故选:C.
【点睛】本题考查了命题的真假判断,正确的命题叫真命题,错误的命题叫做假命题.判断命题的真假关键是要熟悉课本中的性质定理.
10.D
【分析】过E作EM∥AB,则EM∥CD,根据平行线的性质可得∠α+∠β=90°,再由∠α可求解.
【详解】解:由题意知:AB∥CD,∠FEG=90°,
过E作EM∥AB,则EM∥CD,
∴∠FEM=∠α,∠GEM=∠β,
∵∠FEM+∠GEM=∠FEG=90°,
∴∠α+∠β=90°,
∵∠α=44°,
∴∠β=90°-44°=46°.
故选:D.
【点睛】本题主要考查平行线的性质,解题的关键是准确作出辅助线,掌握两直线平行,同位角相等定理的应用.
11.
【分析】由余角的性质可得,,再由,可得,即可求出答案.
【详解】解:如图,
根据题意得:,
∵,
∴,
∵,
∴,
∴,
∴
故答案为:105
【点睛】本题考查了余角的性质,平行线的性质,解题的关键是掌握余角的性质,平行线的性质.
12.23°
【分析】过C作直线AD的平行线CP,利用平行线的性质得到和∠DAC、∠EBC相等的角,然后结合这些等角和∠ACB的位置关系,可求解.
【详解】过C作直线AD的平行线CP,
∵AD∥BE, ∴AD∥BE∥PC,
∵AD∥PC, ∴∠ACP=∠DAC,
同理可得:∠BCP=∠EBC,
∵∠ACB=∠ACP+∠EBC, ∠ACB=45°, ∠DAC=22°,
∴∠EBC=∠ACB-∠DAC =45°-22°=23°.
【点睛】本题考查了平行线的性质,解题的关键是正确作出辅助线,灵活运用平行线的性质.
13.①②④
【分析】本题主要利用平行线的性质以及平行线的判定,采用逐一检验法进行做题.
【详解】解:①,此结论正确;
②,此结论正确;
③,而,此结论错误,
④,此结论正确.
故答案为:①②④.
【点睛】本题考查平行线的判定与性质,解题的关键是正确识别“三线八角”中的同位角、内错角、同旁内角.
14.
【分析】本题考查了矩形的性质和平行线的性质“两直线平行,同旁内角互补”的应用,关键是得出与互补.
根据三角形的内角和得到,根据平角的定义得到,根据平行线的性质即可得到结论.
【详解】解:∵,
∴,
∵,
∴,
∵,
∴,
故答案为:.
15.120.
【详解】试题解析:∵l1∥l2,
∴∠1=∠3=120°,
∵∠3=∠2,
∴∠2=120°.
考点:1.平行线的性质;2.对顶角、邻补角.
16.70°
【详解】试题分析:根据图形可得∠1的对顶角和∠2是同位角,从而根据对顶角相等及同位角相等的知识可得出∠2=180°-110°=70°.
考点:平行线的性质
17. 3 2
【分析】两个完全一样的三角形可以拼成一个平行四边形,每个三角形的面积是拼成的平行四边形面积的一半;两个完全一样的梯形可以拼成一个平行四边形,每个梯形的面积是拼成的平行四边形面积的一半.因为高相同,所以可以通过比较平行四边形的底的长短,得出平行四边形面积的大小.
【详解】解:图1、2、3的高相等,图2三角形的底是8,8÷2=4,图1梯形的上、下底之和除以2,即为(2+7)÷2=4.5;图3平行四边形的底为5,
∵5>4.5>4;
所以,图3平行四边形的面积最大,图2三角形的面积最小.
故答案是:3,2.
【点睛】本题主要考查平行线的性质及等积法,熟练掌握平行线间的距离相等及等积法是解题的关键.
18.
【分析】根据题意画出图形,然后根据平行线的性质可以求得点B处的小丽看点A处的小明的仰角的度数,本题得以解决.
【详解】解:由题意可得,
∠BAC=32°,
∵AC∥BO,
∴∠ABO=∠BAC,
∴∠ABO=32°,
即点B处的小丽看点A处的小明的仰角等于32度,
故答案为32.
【点睛】本题利用平行线间角的关系求仰角俯角问题,解答本题的关键是明确题意,利用数形结合的思想解答.
19.
【分析】利用平行线的性质,可证得∠DFE+∠FEG=180°,∠FGB+∠DFG=180°,就可求出∠DFE的度数,再利用角平分线的定义求出∠DFG的度数,由∠FGB+∠DFG=180°可求出结果.
【详解】解:∵AB∥CD
∴∠DFE+∠FEG=180°,∠FGB+∠DFG=180°
∴∠DFE=180°-70°=110°
∵ FG是∠EFD的平分线
∴∠DFG=
∵∠FGB+∠DFG=180°
∴∠FGB=180°-55°=125°
故答案为125°
【点睛】此题考查了平行线与角平分线的性质,解题的关键是掌握两直线平行,同旁内角互补定理的应用.
20./70度
【分析】根据角平分线的定义得出,进而利用平行线的性质解答即可.
【详解】解:∵平分,,
∴,
∵,
∴,
故答案为:.
【点睛】本题考查平行线的性质,关键是根据两直线平行,同旁内角互补解答.
21.(1)见解析;(2)∠B=46°,∠BCD=134°
【分析】(1)根据平行线的性质得到∠B+∠BAD=180°,∠D+∠BAD=180°,再根据等量代换得到结果;
(2)设∠B=x,根据题意表示出∠CAD和∠ACD,根据∠B+∠BAD=180°,得到方程,解之可得∠B,再根据两直线平行,同旁内角互补得到∠BCD.
【详解】解:(1)∵AB∥CD,AD∥BC,
∴∠B+∠BAD=180°,∠D+∠BAD=180°,
∴∠B=∠D;
(2)设∠B=x,
∵的2倍与的互余,
∴∠CAD=,
∵比的2倍多,
∴∠BAC=∠ACD=2x+20°,
∵∠B+∠BAD=180°,
则x++2x+20°=180°,
解得:x=46°,即∠B=46°,
∵AB∥CD,
∴∠BCD=180°-∠B=134°.
【点睛】本题考查了平行线的性质,一元一次方程的应用,熟练掌握平行线的性质是解题的关键.
22.见解析
【分析】首先根据同位角相等,两直线平行, 再根两直线平行,内错角相等得到=.最后根据两直线平行,同位角相等得到,再进行等量代换即可.
【详解】证明:∵于点A,于点F,
∴.
∴, (同位角相等,两直线平行)
∴=.
(两直线平行,内错角相等)
∵,
∴.
∵,
∴.
【点睛】本题考查了平行线的判定和性质的综合应用,掌握相关知识是解题的关键.
23.(1),证明见解析;(2),证明见解析.
【分析】(1)过点F作AB的平行线FH,由平行线的性质可得AB∥FH∥CD,由两直线平行,内错角相等,得到∠BEF=∠EFH,∠FGD=∠HFG,所以∠BEF+∠FGD=∠EFH+∠HFG,即∠EFG=∠FGD+∠BEF.
(2)思路同(1)根据∠EFG=∠FGD+∠BEF,求出∠EFG=90°从而得出EF⊥FG.
【详解】(1)解:
证明:过点作的平行线
,
(平行于同一条直线的两条直线互相平行)
(已作)
(两直线平行,内错角相等)
(已证)
(两直线平行,内错角相等
(等量代换)
即:
(2)
证明:过点作的平行线
,
(平行于同一条直线的两条直线互相平行)
(平角的定义)
(已作)
(两直线平行,内错角相等)
(已证)
(两直线平行,内错角相等)
(等量代换)
即:
(垂直的定义)
【点睛】本题主要考查的是平行线的性质:两直线平行,内错角相等.
24.(1)见解析
(2)见解析
(3)135°
【分析】(1)过点P作PE//CD于点E,易得AB//PE,CD//PE,通过两直线平行同旁内角互补即可得出结论;
(2)过点M作MF//CD,易得AB//MF,CD//MF,通过两直线平行内错角相等和同旁内角互补即可得出结论;(3)延长AM交CD于点G,延长AP与CD延长线交于点H,易得180°-∠BAM+∠MDG=150°再通过已知条件得出∠BAP-∠NDC=45°,最后∠APC=∠PHC+∠PCH=180°-∠BAP+∠NDC=180°-(∠BAP-∠NDC),代入即可求得答案.
【详解】(1)过点P作PE//CD于点E,
∴∠EPC+∠DCP=180°,
∵,
∴AB//PE,
∴∠BAP+∠APE=180°,
∴∠BAP+∠APE+∠EPC+∠DCP=360°,
∴;
(2)过点M作MF//CD,
∴∠FMD=∠CDM,
∵,
∴AB//MF,
∴∠BAM+∠AMF=180°,
∴∠BAM+∠AMD-∠FMD=180°,
∴;
(3)延长AM交CD于点G,延长AP与CD延长线交于点H,
∵,
∴∠BAG+∠AGD=180°,
∵∠AMD=∠MGD+∠MDG=150°,
∴180°-∠BAM+∠MDG=150°,
∵,
∴∠CDM=∠NDC,
∵,
∴180°-=150°,
∴=30°,
∴∠BAP-∠NDC=45°,
∵,
∴∠BAP+∠PHC=180°,
∵PC//ND,
∴∠PCH=∠NDC,
∴∠APC=∠PHC+∠PCH=180°-∠BAP+∠NDC=180°-(∠BAP-∠NDC)=180°-45°=135°.
【点睛】本题考查了平行线的性质,解题的关键是添加适当辅助线,构造平行线解决问题.
25.,
【分析】根据得到,从而得到,即可得到,根据得到,从而得到,再根据即可得到.
【详解】解:∵
∴
∴
∵,
∴
∵
∴
∵,且
∴
∵
∴
【点睛】本题主要考查了平行线的性质,解题的关键在于能够熟练掌握平行线的性质进行求解.
答案第1页,共2页
答案第1页,共2页
(共25题,满分100分)
题号 一 二 三 总分
得分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.注意保持试卷整洁
一、单选题
1.如图,直线被直线所截,,,则的度数为( )
A. B. C. D.
2.如图,Rt△ABC中,∠ACB=90°,DE过点C且平行于AB,若∠BCE=35°,则∠A的度数为( )
A. B. C. D.
3.如图,桌面上有木条b固定,木条a在桌面上绕点O旋转n°(0<n<90)后与b平行,则n=( )
A.20 B.30 C.70 D.80
4.下列各命题的逆命题成立的是( )
A.对顶角相等 B.如果两个数相等,那么它们的绝对值相等
C.两直线平行,同位角相等 D.如果两个角都是,那么这两个角相等
5.如图,∠AOB的一边OA为平面镜,∠AOB=37°36′,在OB上有一点E,从E点射出一束光线经OA上一点D反射,反射光线DC恰好与OB平行,则∠DEB的度数是( )
A.74°12′ B.74°36′ C.75°12′ D.75°36′
6.用反证法证明某个命题的结论“”时,第一步应假设( )
A. B. C. D.
7.如图,一束光线与水平面成 的角度照射地面,现在地面AB上支放一个平面镜CD,使这束光线经过平面镜反射后成水平光线,则平面镜CD与地面AB所成角∠DCB的度数等于( )
A. B.45° C.50° D.60°
8.有下列四个命题:
①、同位角相等;②、如果两个角的和是 180 度,那么这两个角是邻补角;
③、在同一平面内,平行于同一条直线的两条直线互相平行;
④、在同一平面内,垂直于同一条直线的两条直线互相垂直. 其中是真命题的个数有( )个
A.0 B.1 C.2 D.3
9.下列是假命题的是( ).
A.直角都相等 B.同角的余角相等
C.相等的角是对顶角 D.过直线外一点,有且只有一条直线与已知直线平行
10.将一个直角三角板和一把直尺如图放置,如果∠a=44°,则∠β的度数是( )
A.43° B.44° C.45° D.46°
二、填空题
11.将一个含有角的直角三角板如图所示放置,其中一个角的顶点落在直线a上,含角的顶点落在直线b上.若,则的度数为 .
12.如图,已知AD∥BE,点C是直线FG上的动点,若在点C的移动过程中,存在某时刻使得∠ACB=45°, ∠DAC=22°,则∠EBC的度数为 .
13.如图,下列推理中,请写出你认为是正确推理的编号 .
①因为,所以;
②因为,所以;
③因为,所以;
④因为,所以.
14.如图,含有角的直角三角板的两个顶点放在一个长方形的对边上,点为直角顶点,,延长交于点,如果,那么的度数是 .
15.如图,直线l1∥l2,∠1=120°,则∠2= 度.
16.如图, a∥b,直线c与直线a,b相交,已知,则 .
17.下面两条平行线之间的三个图形,图 的面积最大,图 的面积最小.
18.小明在楼上点处行到楼下点处的小丽的俯角是,那么点处的小丽看点处的小明的仰角是 度.
19.如图,AB∥CD,直线PQ分别交AB,CD于点E,F,FG是∠EFD的平分线,交AB于点G,若∠FEG=70°,那么∠FGB等于 .
20.如图,直线,平分,若,则的度数是 .
三、解答题
21.如图,已知,.
(1)求证:;
(2)连结,若的2倍与的互余,比的2倍多,求和的度数.
22.如图,已知于点A,AE∥CD交于点E,且于点F.
求证:.
证明:∵于点A,于点F,(已知)
∴.(垂直的定义)
∴AD∥EF,( )
∴__________( )
∵AE∥CD,(已知)
∴________.(两直线平行,同位角相等)
∵,
∴.(等量代换)
23.(1)如图,试判断、、之间的关系.并说明理由.
(2)如图,,.试判断和的位置关系,并说明理由.
24.如图,已知,.
(1)求证:;
(2)求证:;
(3)当,,且时,求的度数.
25.如图,,点E、F分别在线段、上,连结交于G,.若,,,求和的度数.
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
) (
学校:___________姓名:___________班级:___________考号:___________
) (
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
第1页 共4页 ◎ 第2页 共4页
第1页 共4页 ◎ 第2页 共4页
参考答案:
1.B
【分析】根据“两直线平行,内错角相等”和“邻补角互补”来求∠2的度数.
【详解】解:,
,
故选择:B
【点睛】本题考查了平行线的性质.平行线性质定理:定理1:两条平行线被第三条直线所截,同位角相等. 简单说成:两直线平行,同位角相等.定理2:两条平行线被地三条直线所截,同旁内角互补.简单说成:两直线平行,同旁内角互补.定理3:两条平行线被第三条直线所截,内错角相等. 简单说成:两直线平行,内错角相等.
2.C
【详解】分析:题中有三个条件,图形为常见图形,可先由AB∥DE,∠BCE=35°,根据两直线平行,内错角相等求出∠B,然后根据三角形内角和为180°求出∠A.
详解:∵AB∥DE,∠BCE=35°,∴∠B=∠BCE=35°(两直线平行,内错角相等).
又∵∠ACB=90°,∴∠A=90°﹣35°=55°(在直角三角形中,两个锐角互余).
故选C.
点睛:看到两直线平行时,应该想到它们的性质,由两直线平行的关系得到角之间的数量关系,从而达到解决问题的目的.
3.B
【详解】如图当a逆时针旋转至c位置时与b平行,旋转角为∠3,
∵c∥b,∴∠2=∠1=70°,
∵∠1+∠3=100°,∴∠3=30°.
∴n=30.
故选B.
点睛:本题关键在于结合旋转与平行线的性质解题,并且要注意旋转角的范围.
4.C
【分析】分别写出下列命题的逆命题,然后判断真假即可.
【详解】解:A.逆命题为相等的两个角是对顶角,逆命题不成立,不符合题意;
B.逆命题为两个数的绝对值相等,那么这两个相等,逆命题不成立,不符合题意;
C.逆命题是同位角相等,两直线平行,逆命题成立,符合题意;
D.逆命题为两个角相等,那么两个角都是,逆命题不成立,不符合题意.
故选:C.
【点睛】本题考查命题与定理的知识,解题的关键是能够写出该命题的逆命题并作出正确的判断.
5.C
【详解】试题分析:过点D作DF⊥AO交OB于点F.∵入射角等于反射角,∴∠1=∠3,∵CD∥OB,∴∠1=∠2(两直线平行,内错角相等);∴∠2=∠3(等量代换);在Rt△DOF中,∠ODF=90°,∠AOB=37°36′,∴∠2=90°﹣37°36′=52°24′;∴在△DEF中,∠DEB=180°﹣2∠2=75°12′.故选C.
考点:1.平行线的性质;2.度分秒的换算;3.跨学科.
6.D
【分析】根据反证法的步骤可直接进行排除选项.
【详解】解:用反证法证明某个命题的结论“”时,第一步应假设;
故选D.
【点睛】本题主要考查反证法,熟练掌握反证法是解题的关键.
7.A
【详解】
∵入射角等于反射角,
∴∠1=∠2,
∵光线经过平面镜CD反射后成水平光线平行,
∴∠2=∠4,
又∵∠1=∠3(对顶角相等),
∴∠3=∠4,
∴∠2=∠3,
∵光线与水平面成60°的角度照射地面,
∴∠3=60°÷2=30°,
∴∠4=30°,即∠DCB=30°
故选A
8.B
【分析】根据同位角的性质、补角的定义、垂直和平行的性质求解即可.
【详解】①、两直线平行,同位角相等,错误;
②、如果两个角的和是 180 度,那么这两个角是补角,错误;
③、在同一平面内,平行于同一条直线的两条直线互相平行,正确;
④、在同一平面内,垂直于同一条直线的两条直线互相平行,错误.
其中是真命题的有1个
故答案为:B.
【点睛】本题考查了,掌握同位角的性质、补角的定义、垂直和平行的性质是解题的关键.
9.C
【分析】根据直角、余角的概念、对顶角的概念、平行线的判定进行判断.
【详解】A、直角都相等,是真命题;
B、同角的余角相等,是真命题;
C、相等的角不一定是对顶角,则相等的角是对顶角是假命题;
D、过直线外一点有且只有一条直线与这条直线平行,是真命题;
故选:C.
【点睛】本题考查了命题的真假判断,正确的命题叫真命题,错误的命题叫做假命题.判断命题的真假关键是要熟悉课本中的性质定理.
10.D
【分析】过E作EM∥AB,则EM∥CD,根据平行线的性质可得∠α+∠β=90°,再由∠α可求解.
【详解】解:由题意知:AB∥CD,∠FEG=90°,
过E作EM∥AB,则EM∥CD,
∴∠FEM=∠α,∠GEM=∠β,
∵∠FEM+∠GEM=∠FEG=90°,
∴∠α+∠β=90°,
∵∠α=44°,
∴∠β=90°-44°=46°.
故选:D.
【点睛】本题主要考查平行线的性质,解题的关键是准确作出辅助线,掌握两直线平行,同位角相等定理的应用.
11.
【分析】由余角的性质可得,,再由,可得,即可求出答案.
【详解】解:如图,
根据题意得:,
∵,
∴,
∵,
∴,
∴,
∴
故答案为:105
【点睛】本题考查了余角的性质,平行线的性质,解题的关键是掌握余角的性质,平行线的性质.
12.23°
【分析】过C作直线AD的平行线CP,利用平行线的性质得到和∠DAC、∠EBC相等的角,然后结合这些等角和∠ACB的位置关系,可求解.
【详解】过C作直线AD的平行线CP,
∵AD∥BE, ∴AD∥BE∥PC,
∵AD∥PC, ∴∠ACP=∠DAC,
同理可得:∠BCP=∠EBC,
∵∠ACB=∠ACP+∠EBC, ∠ACB=45°, ∠DAC=22°,
∴∠EBC=∠ACB-∠DAC =45°-22°=23°.
【点睛】本题考查了平行线的性质,解题的关键是正确作出辅助线,灵活运用平行线的性质.
13.①②④
【分析】本题主要利用平行线的性质以及平行线的判定,采用逐一检验法进行做题.
【详解】解:①,此结论正确;
②,此结论正确;
③,而,此结论错误,
④,此结论正确.
故答案为:①②④.
【点睛】本题考查平行线的判定与性质,解题的关键是正确识别“三线八角”中的同位角、内错角、同旁内角.
14.
【分析】本题考查了矩形的性质和平行线的性质“两直线平行,同旁内角互补”的应用,关键是得出与互补.
根据三角形的内角和得到,根据平角的定义得到,根据平行线的性质即可得到结论.
【详解】解:∵,
∴,
∵,
∴,
∵,
∴,
故答案为:.
15.120.
【详解】试题解析:∵l1∥l2,
∴∠1=∠3=120°,
∵∠3=∠2,
∴∠2=120°.
考点:1.平行线的性质;2.对顶角、邻补角.
16.70°
【详解】试题分析:根据图形可得∠1的对顶角和∠2是同位角,从而根据对顶角相等及同位角相等的知识可得出∠2=180°-110°=70°.
考点:平行线的性质
17. 3 2
【分析】两个完全一样的三角形可以拼成一个平行四边形,每个三角形的面积是拼成的平行四边形面积的一半;两个完全一样的梯形可以拼成一个平行四边形,每个梯形的面积是拼成的平行四边形面积的一半.因为高相同,所以可以通过比较平行四边形的底的长短,得出平行四边形面积的大小.
【详解】解:图1、2、3的高相等,图2三角形的底是8,8÷2=4,图1梯形的上、下底之和除以2,即为(2+7)÷2=4.5;图3平行四边形的底为5,
∵5>4.5>4;
所以,图3平行四边形的面积最大,图2三角形的面积最小.
故答案是:3,2.
【点睛】本题主要考查平行线的性质及等积法,熟练掌握平行线间的距离相等及等积法是解题的关键.
18.
【分析】根据题意画出图形,然后根据平行线的性质可以求得点B处的小丽看点A处的小明的仰角的度数,本题得以解决.
【详解】解:由题意可得,
∠BAC=32°,
∵AC∥BO,
∴∠ABO=∠BAC,
∴∠ABO=32°,
即点B处的小丽看点A处的小明的仰角等于32度,
故答案为32.
【点睛】本题利用平行线间角的关系求仰角俯角问题,解答本题的关键是明确题意,利用数形结合的思想解答.
19.
【分析】利用平行线的性质,可证得∠DFE+∠FEG=180°,∠FGB+∠DFG=180°,就可求出∠DFE的度数,再利用角平分线的定义求出∠DFG的度数,由∠FGB+∠DFG=180°可求出结果.
【详解】解:∵AB∥CD
∴∠DFE+∠FEG=180°,∠FGB+∠DFG=180°
∴∠DFE=180°-70°=110°
∵ FG是∠EFD的平分线
∴∠DFG=
∵∠FGB+∠DFG=180°
∴∠FGB=180°-55°=125°
故答案为125°
【点睛】此题考查了平行线与角平分线的性质,解题的关键是掌握两直线平行,同旁内角互补定理的应用.
20./70度
【分析】根据角平分线的定义得出,进而利用平行线的性质解答即可.
【详解】解:∵平分,,
∴,
∵,
∴,
故答案为:.
【点睛】本题考查平行线的性质,关键是根据两直线平行,同旁内角互补解答.
21.(1)见解析;(2)∠B=46°,∠BCD=134°
【分析】(1)根据平行线的性质得到∠B+∠BAD=180°,∠D+∠BAD=180°,再根据等量代换得到结果;
(2)设∠B=x,根据题意表示出∠CAD和∠ACD,根据∠B+∠BAD=180°,得到方程,解之可得∠B,再根据两直线平行,同旁内角互补得到∠BCD.
【详解】解:(1)∵AB∥CD,AD∥BC,
∴∠B+∠BAD=180°,∠D+∠BAD=180°,
∴∠B=∠D;
(2)设∠B=x,
∵的2倍与的互余,
∴∠CAD=,
∵比的2倍多,
∴∠BAC=∠ACD=2x+20°,
∵∠B+∠BAD=180°,
则x++2x+20°=180°,
解得:x=46°,即∠B=46°,
∵AB∥CD,
∴∠BCD=180°-∠B=134°.
【点睛】本题考查了平行线的性质,一元一次方程的应用,熟练掌握平行线的性质是解题的关键.
22.见解析
【分析】首先根据同位角相等,两直线平行, 再根两直线平行,内错角相等得到=.最后根据两直线平行,同位角相等得到,再进行等量代换即可.
【详解】证明:∵于点A,于点F,
∴.
∴, (同位角相等,两直线平行)
∴=.
(两直线平行,内错角相等)
∵,
∴.
∵,
∴.
【点睛】本题考查了平行线的判定和性质的综合应用,掌握相关知识是解题的关键.
23.(1),证明见解析;(2),证明见解析.
【分析】(1)过点F作AB的平行线FH,由平行线的性质可得AB∥FH∥CD,由两直线平行,内错角相等,得到∠BEF=∠EFH,∠FGD=∠HFG,所以∠BEF+∠FGD=∠EFH+∠HFG,即∠EFG=∠FGD+∠BEF.
(2)思路同(1)根据∠EFG=∠FGD+∠BEF,求出∠EFG=90°从而得出EF⊥FG.
【详解】(1)解:
证明:过点作的平行线
,
(平行于同一条直线的两条直线互相平行)
(已作)
(两直线平行,内错角相等)
(已证)
(两直线平行,内错角相等
(等量代换)
即:
(2)
证明:过点作的平行线
,
(平行于同一条直线的两条直线互相平行)
(平角的定义)
(已作)
(两直线平行,内错角相等)
(已证)
(两直线平行,内错角相等)
(等量代换)
即:
(垂直的定义)
【点睛】本题主要考查的是平行线的性质:两直线平行,内错角相等.
24.(1)见解析
(2)见解析
(3)135°
【分析】(1)过点P作PE//CD于点E,易得AB//PE,CD//PE,通过两直线平行同旁内角互补即可得出结论;
(2)过点M作MF//CD,易得AB//MF,CD//MF,通过两直线平行内错角相等和同旁内角互补即可得出结论;(3)延长AM交CD于点G,延长AP与CD延长线交于点H,易得180°-∠BAM+∠MDG=150°再通过已知条件得出∠BAP-∠NDC=45°,最后∠APC=∠PHC+∠PCH=180°-∠BAP+∠NDC=180°-(∠BAP-∠NDC),代入即可求得答案.
【详解】(1)过点P作PE//CD于点E,
∴∠EPC+∠DCP=180°,
∵,
∴AB//PE,
∴∠BAP+∠APE=180°,
∴∠BAP+∠APE+∠EPC+∠DCP=360°,
∴;
(2)过点M作MF//CD,
∴∠FMD=∠CDM,
∵,
∴AB//MF,
∴∠BAM+∠AMF=180°,
∴∠BAM+∠AMD-∠FMD=180°,
∴;
(3)延长AM交CD于点G,延长AP与CD延长线交于点H,
∵,
∴∠BAG+∠AGD=180°,
∵∠AMD=∠MGD+∠MDG=150°,
∴180°-∠BAM+∠MDG=150°,
∵,
∴∠CDM=∠NDC,
∵,
∴180°-=150°,
∴=30°,
∴∠BAP-∠NDC=45°,
∵,
∴∠BAP+∠PHC=180°,
∵PC//ND,
∴∠PCH=∠NDC,
∴∠APC=∠PHC+∠PCH=180°-∠BAP+∠NDC=180°-(∠BAP-∠NDC)=180°-45°=135°.
【点睛】本题考查了平行线的性质,解题的关键是添加适当辅助线,构造平行线解决问题.
25.,
【分析】根据得到,从而得到,即可得到,根据得到,从而得到,再根据即可得到.
【详解】解:∵
∴
∴
∵,
∴
∵
∴
∵,且
∴
∵
∴
【点睛】本题主要考查了平行线的性质,解题的关键在于能够熟练掌握平行线的性质进行求解.
答案第1页,共2页
答案第1页,共2页
