5.1相交线同步练习(含解析)人教版数学七年级下册
文档属性
| 名称 | 5.1相交线同步练习(含解析)人教版数学七年级下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 530.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-03 14:44:43 | ||
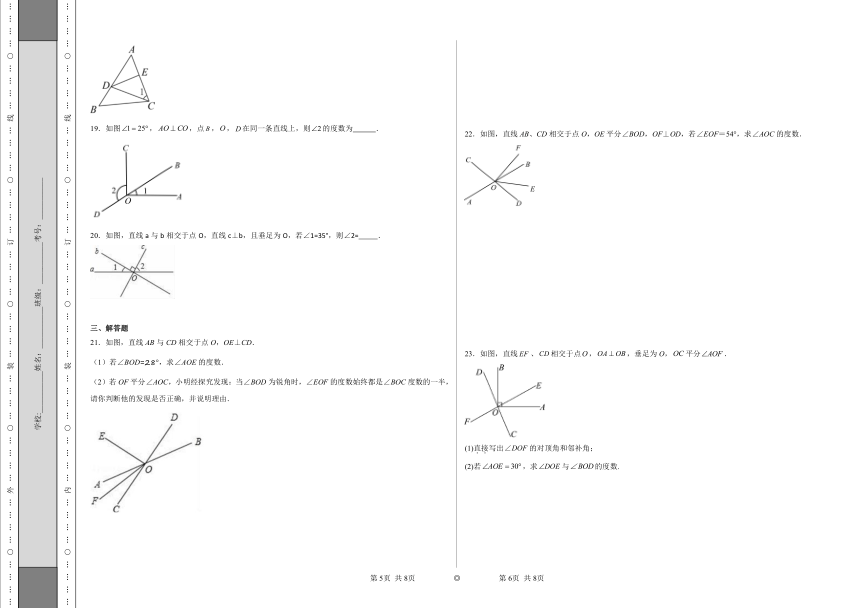
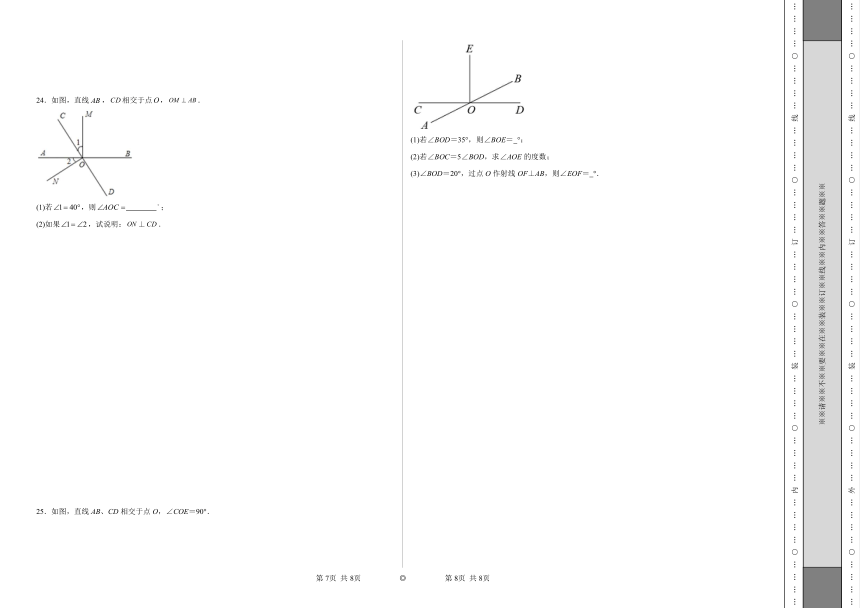
图片预览



文档简介
5.1相交线
(共25题,满分100分)
题号 一 二 三 总分
得分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.注意保持试卷整洁
一、单选题
1.如图,下列说法正确的有( )
①∠1与∠2是同旁内角; ②∠1与∠ACE是内错角;③∠B与∠4是同位角;④∠1与∠3是内错角.
A.①③④ B.③④ C.①②④ D.①②③④
2.如下图所示,直线a,b被直线c所截,下列说法错误的是( )
A.与是邻补角 B.与是对顶角 C.与是同位角 D.与是内错角
3.如图,某工厂计划挖一条排污管道,将工厂(记作点O)产生的工业废水排到小河中,现设计了四条路线、、、,其中最短的一条路线是( )
A. B. C. D.
4.如图,直线与相交于点,,若,则的度数为( )
A. B. C. D.
5.如图,某工程队计划把河水引到水池A中,他们先过点A作,垂足为B,为河岸,然后沿开渠,可以节约人力、物力和财力,这样设计的数学依据是( )
A.两点之间,线段最短
B.在同一平面内,过一点有且只有一条直线垂直于已知直线
C.经过两点有一条直线,并且只有一条直线
D.垂线段最短
6.如图,直线相交于点O,,若,则的度数为( )
A. B. C. D.
7.如所示各图中,∠1与∠2是对顶角的是( )
A. B. C. D.
8.如图所示,,,,,点Р到直线的距离可能是( )
A.5 B.3 C.2 D.4.5
9.如图所示,直线a,b相交于点O,若∠1等于50°,则∠2等于( )
A.50° B.40° C.140° D.130°
10.如图,直线截、分别交于、两点,则的同位角是( )
A. B. C. D.
二、填空题
11.如图,直线AB、CD、EF相交于点O,则∠AOC的对顶角是 ,∠AOE的邻补角是
12.如图,与是对顶角,,,则 .
13.如图,直线,相交于点,若,则的度数是 .
14.如图所示,直线交于点,则 ,根据是 .
15.如图,直线AB和CD相交于O点,OE⊥CD,∠EOF=142°,∠BOD:∠BOF=1:3,则∠AOF的度数为 .
16.如图,直线AB与直线CD相交于点O,E是∠COB内一点,OE⊥AB,∠AOC=26°,则∠EOD的度数是 .
17.如图,点是直线外一点,点A,在直线上,是线段的中点,,垂足为点,则点到直线的距离是线段 的长度.
18.如图,请找出图中∠1的同旁内角有 个;
19.如图,,点,,在同一条直线上,则的度数为 .
20.如图,直线a与b相交于点O,直线c⊥b,且垂足为O,若∠1=35°,则∠2= .
三、解答题
21.如图,直线AB与CD相交于点O,OE⊥CD.
(1)若∠BOD=28°,求∠AOE的度数.
(2)若OF平分∠AOC,小明经探究发现:当∠BOD为锐角时,∠EOF的度数始终都是∠BOC度数的一半,请你判断他的发现是否正确,并说明理由.
22.如图,直线AB、CD相交于点O,OE平分∠BOD,OF⊥OD,若∠EOF=54°,求∠AOC的度数.
23.如图,直线、相交于点,,垂足为O,平分.
(1)直接写出的对顶角和邻补角;
(2)若,求与的度数.
24.如图,直线,相交于点,.
(1)若,则 ;
(2)如果,试说明:⊥.
25.如图,直线AB、CD相交于点O,∠COE=90°.
(1)若∠BOD=35°,则∠BOE= °;
(2)若∠BOC=5∠BOD,求∠AOE的度数;
(3)∠BOD=20°,过点O作射线OF⊥AB,则∠EOF= °.
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
) (
学校:___________姓名:___________班级:___________考号:___________
) (
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
第1页 共4页 ◎ 第2页 共4页
第1页 共4页 ◎ 第2页 共4页
参考答案:
1.D
【分析】根据同旁内角、内错角和同位角的定义逐一判断即可.
【详解】解:由图可得①∠1与∠2是同旁内角,正确;
②∠1与∠ACE是内错角,正确;
③∠B与∠4是同位角,正确;
④∠1与∠3是内错角,正确.
∴①②③④正确.
故选D.
【点睛】本题考查了同旁内角、内错角和同位角的定义,解决本题的关键是掌握以上的定义:
同旁内角:两条直线被第三条直线所截,在截线同旁,且在被截线之内的两角,叫做同旁内角;
内错角:两条直线被第三条直线所截,两个角分别在截线的两侧,且夹在两条被截直线之间,具有这样位置关系的一对角叫做内错角;
同位角:两条直线a,b被第三条直线c所截,在截线c的同旁,且在被截两直线a,b的同一侧的角,我们把这样的两个角称为同位角.
2.C
【分析】根据两直线被第三条直线所截形成的各种角关系的定义求解.
【详解】解:A、∠1与∠4是邻补角,故原题说法正确;
B、∠1与∠3是对顶角,故原题说法正确;
C、∠1与∠7不是同位角,故原题说法错误;
D、∠3与∠5是内错角,故原题说法正确.
故选C.
【点睛】本题考查两直线被第三条直线所截形成的各种角关系的应用,熟练掌握两直线被第三条直线所截形成的各种角关系的定义及辨析是解题关键.
3.B
【分析】本题考查了垂线段最短,据此进行作答即可.
【详解】解:由题意得四条路线、、、,其中最短的一条路线是,
故选:B.
4.B
【分析】根据对顶角相等求解即可.
【详解】解:
又
(对顶角相等)
故选B
【点睛】本题主要考查了对顶角的性质,熟练掌握这一性质是解题的关键.
5.D
【分析】此题主要考查了垂线段的性质,解题的关键是掌握垂线段最短.根据垂线段最短进行解答即可.
【详解】解:某工程队计划把河水引到水池A中,他们先过点A作,垂足为B,为河岸,然后沿开渠,可以节约人力、物力和财力,这样设计的数学依据是:垂线段最短.
故选:D.
6.B
【分析】
根据垂线定义可求得,进而求得,再根据对顶角相等求解即可.
【详解】
解:∵,
∴,
∴,
∵,
∴,
∴,
故选:B.
【点睛】本题考查垂线定义、对顶角相等,熟练掌握垂线定义和对顶角相等是解答的关键.
7.B
【分析】根据对顶角的定义进行判断:两条直线相交后所得的只有一个公共顶点且两个角的两边互为反向延长线,这样的两个角叫做对顶角.
【详解】解:A.∠1与∠2没有公共顶点,不是对顶角;
B.∠1与∠2有公共顶点,并且两边互为反向延长线,是对顶角;
C.∠1与∠2虽然有公共顶点,但两个角的两边不互为反向延长线,不是对顶角;
D.∠1与∠2虽然有公共顶点,但两个角的两边不互为反向延长线,不是对顶角.
故选:B.
【点睛】本题主要考查了对顶角的定义,熟记对顶角的定义是解题的关键.
8.C
【分析】根据直线外一点到直线的距离即为垂线段的长度和垂线段最短的性质进行求解.
【详解】解:因为垂线段最短,
所以点Р到直线的距离为不大于2,
故选:C.
【点睛】此题考查了垂线段最短的性质,此题所给的线段长度中,可能是垂线段,也可能不是.
9.A
【详解】∵∠2与∠1是对顶角,
∴∠2=∠1=50°.
故选A.
【点睛】本题考查对顶角.
10.B
【分析】根据同位角的定义:两条直线a,b被第三条直线c所截(或说a,b相交c),在截线c的同旁,被截两直线a,b的同一侧的角,我们把这样的两个角称为同位角,进行判断即可.
【详解】解:如图所示,
∠1的同位角为∠3,
故选B.
【点睛】本题主要考查了同位角的定义,解题的关键在于能够熟练掌握同位角的定义.
11. ∠BOD; ∠AOF、∠BOE.
【分析】根据对顶角和邻补角的定义进行解答即可.
【详解】由图可知,∠AOC的对顶角是∠BOD,
∠AOE的邻补角是∠AOF、∠BOE,
故答案为∠BOD;∠AOF、∠BOE.
【点睛】本题考查了对顶角及邻补角,判断对顶角和邻补角的关键是看准是由哪两条直线相交而成的角.注意两直线相交,一个角的对顶角只有一个,但邻补角有两个.
12.40°
【分析】先根据对顶角相等的性质得出∠1=∠2,即可求出α的度数.
【详解】解:∵∠1与∠2是对顶角,,∠2=50°,
∴∠1=∠2,
∵,∠2=50°,
∴α+10°=50°,
∴α=40°.
故答案为:40°.
【点睛】本题考查了对顶角相等的性质以及角度的计算.
13.
【分析】根据补角的性质直接计算即可.
【详解】解:由图可知∠1和∠2互补,
∴,
故答案为:.
【点睛】本题考查了补角的内容以及角度的计算,熟练掌握角度的计算是解题的关键.
14. = , 对顶角相等
【分析】根据两直线相交,对顶角相等,即可得到答案.
【详解】解:由题可知,与是对顶角,
∴,
根据是对顶角相等;
故答案为=,对顶角相等;
【点睛】本题考查了对顶角相等,解题的关键是对定理的掌握.
15.102°
【分析】根据垂直的定义,可得∠DOE的度数,根据角的和差,可得∠DOF的度数,根据角的倍分关系,可得∠BOF的度数,根据∠BOF与∠AOF是邻补角,可得答案.
【详解】解:∵OE⊥CD,
∴∠EOD=90°,
∵∠EOF=142°,
∴∠DOF=142°﹣90°=52°,
∵∠BOD:∠BOF=1:3,
∴∠BOD=∠DOF=26°,
∴∠BOF=∠BOD+∠DOF=78°,
∵∠AOF+∠BOF=180°,
∴∠AOF=180°﹣∠BOF=180°﹣78°=102°.
故答案为:102°.
【点睛】本题考查垂直的性质、角的和差、角的倍分关系、邻补角的性质等知识,是基础考点,掌握相关知识是解题关键.
16.116°
【分析】直接利用垂线的定义以及对顶角的性质分析得出答案.
【详解】解:∵直线AB与直线CD相交于点O,
∴∠BOD=∠AOC=26°,
∵OE⊥AB,
∴∠EOB=90°,
∴∠EOD=∠EOB+∠BOD=90°+26°=116°.
故答案为:116°.
【点睛】本题考查垂线定义、对顶角相等,掌握垂线定义和对顶角相等是解答的关键.
17./
【分析】根据点到直线的距离的定义即可解答
【详解】解:∵,垂足为点,
∴点到直线的距离是线段的长度.
故答案为:.
【点睛】本题主要考查了点到直线的距离,自点向直线做垂线段,这条垂线段的长度叫做点到直线的距离.
18.4
【分析】根据同旁内角的定义,两条直线被第三条直线所截,在截线同旁,且在被截线之内的两角,叫做同旁内角.
【详解】解:∠1的同旁内角有,共4个
故答案为:4
【点睛】本题考查了同旁内角的定义,理解定义是解题的关键.
19./度
【分析】根据垂直的定义可得出,即可求出,再根据互为邻补角的两角和为列式计算即可得出答案.
【详解】解:∵,
∴,
∵,
∴,
∵点,,在同一直线上,
∴,
故答案为:.
【点睛】本题考查的知识点是垂线以及邻补角,属于基础题目,易于掌握.
20.55°
【详解】如下图,∵直线a、b、c相交于点O,且c⊥b,
∴∠1+∠2+3∠=180°,∠3=90°,
又∵∠1=35°,
∴∠2=180°-35°-90°=55°.
故答案为55°.
21.(1)62°;(2)正确,
【详解】试题分析:(1)根据对顶角相等求出∠AOC的度数,根据垂直的定义计算即可;
(2)设∠BOD=x°,用x表示出∠AOC和∠BOC,根据邻补角的概念计算即可;
试题解析:
(1)∵∠BOD=28°,
∴∠AOC=∠BOD=28°,
∵OE⊥CD,
∴∠EOC=90°,
∴∠AOE=∠EOC-∠AOC=62°,
(2)正确,
设∠BOD=x°,则∠AOC=∠BOD=x°,∠BOC=180°-x°,
∵OF平分∠AOC,
∴∠FOC=x°,
∴∠EOF=90°-∠FOC=90°-x°,
∴∠EOF=∠BOC.
22.∠AOC的度数为72°.
【分析】依据OF⊥CD,∠EOF=54°,可得∠DOE=90°-54°=36°,再根据OE平分∠BOD,即可得出∠BOD=2∠DOE=72°,依据对顶角相等得到∠AOC.
【详解】解:∵OF⊥CD,∠EOF=54°,
∴∠DOE=90°-54°=36°,
又∵OE平分∠BOD,
∴∠BOD=2∠DOE=72°,
∴∠AOC=72°.
【点睛】本题主要考查了了垂线,角平分线的定义以及余角的综合运用,正确的识别图形是解题的关键.
23.(1)的对顶角是,邻补角是和;
(2),.
【分析】
本题考查的是邻补角、余角的定义,解题的关键就是熟练掌握这些角的位置关系和数量关系.
(1)利用对顶角、邻补角的定义直接写出结果即可;
(2)利用补角、余角的定义求得结果即可.
【详解】(1)
解:的对顶角是,
邻补角是和;
(2)
解:,,
,
,
,,
.
24.(1)50
(2)见解析
【详解】(1)解:∵OM⊥AB,
∴∠AOM=90°,
∴∠1+∠AOC=∠AOM=90°,
∵∠1=40°,
∴∠AOC=50°,
故答案为:50°;
(2)解:∵OM⊥AB,
∴∠AOM=90°,
∴∠1+∠AOC=90°,
∵∠1=∠2,
∴∠2+∠AOC=90°,
即∠CON=90°,
∴ON⊥CD.
【点睛】本题考查垂线的定义,角的和差计算,熟练垂线的定义是解题的关键.
25.(1)55
(2)
(3)20或160
【分析】(1)先求出,再根据互余角的概念即可得;
(2)先根据求出,再根据对顶角相等可得,然后根据角的和差即可得;
(3)分①在的左上方,②在的右下方两种情况,分别根据互余角的概念、角的和差即可得.
【详解】(1)解:,
,
,
,
故答案为:55.
(2)解:,
,
由对顶角相等得:,
,
.
(3)解:由题意,分以下两种情况:
①如图,当在的左上方时,
,
,
,
,
,
,
;
②如图,当在的右下方时,
,
,
,
,
;
综上,或,
故答案为:20或160.
【点睛】本题考查了角的和差、互余角、垂直,熟练掌握角的和差运算是解题关键.
答案第1页,共2页
答案第1页,共2页
(共25题,满分100分)
题号 一 二 三 总分
得分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.注意保持试卷整洁
一、单选题
1.如图,下列说法正确的有( )
①∠1与∠2是同旁内角; ②∠1与∠ACE是内错角;③∠B与∠4是同位角;④∠1与∠3是内错角.
A.①③④ B.③④ C.①②④ D.①②③④
2.如下图所示,直线a,b被直线c所截,下列说法错误的是( )
A.与是邻补角 B.与是对顶角 C.与是同位角 D.与是内错角
3.如图,某工厂计划挖一条排污管道,将工厂(记作点O)产生的工业废水排到小河中,现设计了四条路线、、、,其中最短的一条路线是( )
A. B. C. D.
4.如图,直线与相交于点,,若,则的度数为( )
A. B. C. D.
5.如图,某工程队计划把河水引到水池A中,他们先过点A作,垂足为B,为河岸,然后沿开渠,可以节约人力、物力和财力,这样设计的数学依据是( )
A.两点之间,线段最短
B.在同一平面内,过一点有且只有一条直线垂直于已知直线
C.经过两点有一条直线,并且只有一条直线
D.垂线段最短
6.如图,直线相交于点O,,若,则的度数为( )
A. B. C. D.
7.如所示各图中,∠1与∠2是对顶角的是( )
A. B. C. D.
8.如图所示,,,,,点Р到直线的距离可能是( )
A.5 B.3 C.2 D.4.5
9.如图所示,直线a,b相交于点O,若∠1等于50°,则∠2等于( )
A.50° B.40° C.140° D.130°
10.如图,直线截、分别交于、两点,则的同位角是( )
A. B. C. D.
二、填空题
11.如图,直线AB、CD、EF相交于点O,则∠AOC的对顶角是 ,∠AOE的邻补角是
12.如图,与是对顶角,,,则 .
13.如图,直线,相交于点,若,则的度数是 .
14.如图所示,直线交于点,则 ,根据是 .
15.如图,直线AB和CD相交于O点,OE⊥CD,∠EOF=142°,∠BOD:∠BOF=1:3,则∠AOF的度数为 .
16.如图,直线AB与直线CD相交于点O,E是∠COB内一点,OE⊥AB,∠AOC=26°,则∠EOD的度数是 .
17.如图,点是直线外一点,点A,在直线上,是线段的中点,,垂足为点,则点到直线的距离是线段 的长度.
18.如图,请找出图中∠1的同旁内角有 个;
19.如图,,点,,在同一条直线上,则的度数为 .
20.如图,直线a与b相交于点O,直线c⊥b,且垂足为O,若∠1=35°,则∠2= .
三、解答题
21.如图,直线AB与CD相交于点O,OE⊥CD.
(1)若∠BOD=28°,求∠AOE的度数.
(2)若OF平分∠AOC,小明经探究发现:当∠BOD为锐角时,∠EOF的度数始终都是∠BOC度数的一半,请你判断他的发现是否正确,并说明理由.
22.如图,直线AB、CD相交于点O,OE平分∠BOD,OF⊥OD,若∠EOF=54°,求∠AOC的度数.
23.如图,直线、相交于点,,垂足为O,平分.
(1)直接写出的对顶角和邻补角;
(2)若,求与的度数.
24.如图,直线,相交于点,.
(1)若,则 ;
(2)如果,试说明:⊥.
25.如图,直线AB、CD相交于点O,∠COE=90°.
(1)若∠BOD=35°,则∠BOE= °;
(2)若∠BOC=5∠BOD,求∠AOE的度数;
(3)∠BOD=20°,过点O作射线OF⊥AB,则∠EOF= °.
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
) (
学校:___________姓名:___________班级:___________考号:___________
) (
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
第1页 共4页 ◎ 第2页 共4页
第1页 共4页 ◎ 第2页 共4页
参考答案:
1.D
【分析】根据同旁内角、内错角和同位角的定义逐一判断即可.
【详解】解:由图可得①∠1与∠2是同旁内角,正确;
②∠1与∠ACE是内错角,正确;
③∠B与∠4是同位角,正确;
④∠1与∠3是内错角,正确.
∴①②③④正确.
故选D.
【点睛】本题考查了同旁内角、内错角和同位角的定义,解决本题的关键是掌握以上的定义:
同旁内角:两条直线被第三条直线所截,在截线同旁,且在被截线之内的两角,叫做同旁内角;
内错角:两条直线被第三条直线所截,两个角分别在截线的两侧,且夹在两条被截直线之间,具有这样位置关系的一对角叫做内错角;
同位角:两条直线a,b被第三条直线c所截,在截线c的同旁,且在被截两直线a,b的同一侧的角,我们把这样的两个角称为同位角.
2.C
【分析】根据两直线被第三条直线所截形成的各种角关系的定义求解.
【详解】解:A、∠1与∠4是邻补角,故原题说法正确;
B、∠1与∠3是对顶角,故原题说法正确;
C、∠1与∠7不是同位角,故原题说法错误;
D、∠3与∠5是内错角,故原题说法正确.
故选C.
【点睛】本题考查两直线被第三条直线所截形成的各种角关系的应用,熟练掌握两直线被第三条直线所截形成的各种角关系的定义及辨析是解题关键.
3.B
【分析】本题考查了垂线段最短,据此进行作答即可.
【详解】解:由题意得四条路线、、、,其中最短的一条路线是,
故选:B.
4.B
【分析】根据对顶角相等求解即可.
【详解】解:
又
(对顶角相等)
故选B
【点睛】本题主要考查了对顶角的性质,熟练掌握这一性质是解题的关键.
5.D
【分析】此题主要考查了垂线段的性质,解题的关键是掌握垂线段最短.根据垂线段最短进行解答即可.
【详解】解:某工程队计划把河水引到水池A中,他们先过点A作,垂足为B,为河岸,然后沿开渠,可以节约人力、物力和财力,这样设计的数学依据是:垂线段最短.
故选:D.
6.B
【分析】
根据垂线定义可求得,进而求得,再根据对顶角相等求解即可.
【详解】
解:∵,
∴,
∴,
∵,
∴,
∴,
故选:B.
【点睛】本题考查垂线定义、对顶角相等,熟练掌握垂线定义和对顶角相等是解答的关键.
7.B
【分析】根据对顶角的定义进行判断:两条直线相交后所得的只有一个公共顶点且两个角的两边互为反向延长线,这样的两个角叫做对顶角.
【详解】解:A.∠1与∠2没有公共顶点,不是对顶角;
B.∠1与∠2有公共顶点,并且两边互为反向延长线,是对顶角;
C.∠1与∠2虽然有公共顶点,但两个角的两边不互为反向延长线,不是对顶角;
D.∠1与∠2虽然有公共顶点,但两个角的两边不互为反向延长线,不是对顶角.
故选:B.
【点睛】本题主要考查了对顶角的定义,熟记对顶角的定义是解题的关键.
8.C
【分析】根据直线外一点到直线的距离即为垂线段的长度和垂线段最短的性质进行求解.
【详解】解:因为垂线段最短,
所以点Р到直线的距离为不大于2,
故选:C.
【点睛】此题考查了垂线段最短的性质,此题所给的线段长度中,可能是垂线段,也可能不是.
9.A
【详解】∵∠2与∠1是对顶角,
∴∠2=∠1=50°.
故选A.
【点睛】本题考查对顶角.
10.B
【分析】根据同位角的定义:两条直线a,b被第三条直线c所截(或说a,b相交c),在截线c的同旁,被截两直线a,b的同一侧的角,我们把这样的两个角称为同位角,进行判断即可.
【详解】解:如图所示,
∠1的同位角为∠3,
故选B.
【点睛】本题主要考查了同位角的定义,解题的关键在于能够熟练掌握同位角的定义.
11. ∠BOD; ∠AOF、∠BOE.
【分析】根据对顶角和邻补角的定义进行解答即可.
【详解】由图可知,∠AOC的对顶角是∠BOD,
∠AOE的邻补角是∠AOF、∠BOE,
故答案为∠BOD;∠AOF、∠BOE.
【点睛】本题考查了对顶角及邻补角,判断对顶角和邻补角的关键是看准是由哪两条直线相交而成的角.注意两直线相交,一个角的对顶角只有一个,但邻补角有两个.
12.40°
【分析】先根据对顶角相等的性质得出∠1=∠2,即可求出α的度数.
【详解】解:∵∠1与∠2是对顶角,,∠2=50°,
∴∠1=∠2,
∵,∠2=50°,
∴α+10°=50°,
∴α=40°.
故答案为:40°.
【点睛】本题考查了对顶角相等的性质以及角度的计算.
13.
【分析】根据补角的性质直接计算即可.
【详解】解:由图可知∠1和∠2互补,
∴,
故答案为:.
【点睛】本题考查了补角的内容以及角度的计算,熟练掌握角度的计算是解题的关键.
14. = , 对顶角相等
【分析】根据两直线相交,对顶角相等,即可得到答案.
【详解】解:由题可知,与是对顶角,
∴,
根据是对顶角相等;
故答案为=,对顶角相等;
【点睛】本题考查了对顶角相等,解题的关键是对定理的掌握.
15.102°
【分析】根据垂直的定义,可得∠DOE的度数,根据角的和差,可得∠DOF的度数,根据角的倍分关系,可得∠BOF的度数,根据∠BOF与∠AOF是邻补角,可得答案.
【详解】解:∵OE⊥CD,
∴∠EOD=90°,
∵∠EOF=142°,
∴∠DOF=142°﹣90°=52°,
∵∠BOD:∠BOF=1:3,
∴∠BOD=∠DOF=26°,
∴∠BOF=∠BOD+∠DOF=78°,
∵∠AOF+∠BOF=180°,
∴∠AOF=180°﹣∠BOF=180°﹣78°=102°.
故答案为:102°.
【点睛】本题考查垂直的性质、角的和差、角的倍分关系、邻补角的性质等知识,是基础考点,掌握相关知识是解题关键.
16.116°
【分析】直接利用垂线的定义以及对顶角的性质分析得出答案.
【详解】解:∵直线AB与直线CD相交于点O,
∴∠BOD=∠AOC=26°,
∵OE⊥AB,
∴∠EOB=90°,
∴∠EOD=∠EOB+∠BOD=90°+26°=116°.
故答案为:116°.
【点睛】本题考查垂线定义、对顶角相等,掌握垂线定义和对顶角相等是解答的关键.
17./
【分析】根据点到直线的距离的定义即可解答
【详解】解:∵,垂足为点,
∴点到直线的距离是线段的长度.
故答案为:.
【点睛】本题主要考查了点到直线的距离,自点向直线做垂线段,这条垂线段的长度叫做点到直线的距离.
18.4
【分析】根据同旁内角的定义,两条直线被第三条直线所截,在截线同旁,且在被截线之内的两角,叫做同旁内角.
【详解】解:∠1的同旁内角有,共4个
故答案为:4
【点睛】本题考查了同旁内角的定义,理解定义是解题的关键.
19./度
【分析】根据垂直的定义可得出,即可求出,再根据互为邻补角的两角和为列式计算即可得出答案.
【详解】解:∵,
∴,
∵,
∴,
∵点,,在同一直线上,
∴,
故答案为:.
【点睛】本题考查的知识点是垂线以及邻补角,属于基础题目,易于掌握.
20.55°
【详解】如下图,∵直线a、b、c相交于点O,且c⊥b,
∴∠1+∠2+3∠=180°,∠3=90°,
又∵∠1=35°,
∴∠2=180°-35°-90°=55°.
故答案为55°.
21.(1)62°;(2)正确,
【详解】试题分析:(1)根据对顶角相等求出∠AOC的度数,根据垂直的定义计算即可;
(2)设∠BOD=x°,用x表示出∠AOC和∠BOC,根据邻补角的概念计算即可;
试题解析:
(1)∵∠BOD=28°,
∴∠AOC=∠BOD=28°,
∵OE⊥CD,
∴∠EOC=90°,
∴∠AOE=∠EOC-∠AOC=62°,
(2)正确,
设∠BOD=x°,则∠AOC=∠BOD=x°,∠BOC=180°-x°,
∵OF平分∠AOC,
∴∠FOC=x°,
∴∠EOF=90°-∠FOC=90°-x°,
∴∠EOF=∠BOC.
22.∠AOC的度数为72°.
【分析】依据OF⊥CD,∠EOF=54°,可得∠DOE=90°-54°=36°,再根据OE平分∠BOD,即可得出∠BOD=2∠DOE=72°,依据对顶角相等得到∠AOC.
【详解】解:∵OF⊥CD,∠EOF=54°,
∴∠DOE=90°-54°=36°,
又∵OE平分∠BOD,
∴∠BOD=2∠DOE=72°,
∴∠AOC=72°.
【点睛】本题主要考查了了垂线,角平分线的定义以及余角的综合运用,正确的识别图形是解题的关键.
23.(1)的对顶角是,邻补角是和;
(2),.
【分析】
本题考查的是邻补角、余角的定义,解题的关键就是熟练掌握这些角的位置关系和数量关系.
(1)利用对顶角、邻补角的定义直接写出结果即可;
(2)利用补角、余角的定义求得结果即可.
【详解】(1)
解:的对顶角是,
邻补角是和;
(2)
解:,,
,
,
,,
.
24.(1)50
(2)见解析
【详解】(1)解:∵OM⊥AB,
∴∠AOM=90°,
∴∠1+∠AOC=∠AOM=90°,
∵∠1=40°,
∴∠AOC=50°,
故答案为:50°;
(2)解:∵OM⊥AB,
∴∠AOM=90°,
∴∠1+∠AOC=90°,
∵∠1=∠2,
∴∠2+∠AOC=90°,
即∠CON=90°,
∴ON⊥CD.
【点睛】本题考查垂线的定义,角的和差计算,熟练垂线的定义是解题的关键.
25.(1)55
(2)
(3)20或160
【分析】(1)先求出,再根据互余角的概念即可得;
(2)先根据求出,再根据对顶角相等可得,然后根据角的和差即可得;
(3)分①在的左上方,②在的右下方两种情况,分别根据互余角的概念、角的和差即可得.
【详解】(1)解:,
,
,
,
故答案为:55.
(2)解:,
,
由对顶角相等得:,
,
.
(3)解:由题意,分以下两种情况:
①如图,当在的左上方时,
,
,
,
,
,
,
;
②如图,当在的右下方时,
,
,
,
,
;
综上,或,
故答案为:20或160.
【点睛】本题考查了角的和差、互余角、垂直,熟练掌握角的和差运算是解题关键.
答案第1页,共2页
答案第1页,共2页
