北京市第三十一中学2023-2024学年高二下学期期中考试数学试卷(PDF版无答案)
文档属性
| 名称 | 北京市第三十一中学2023-2024学年高二下学期期中考试数学试卷(PDF版无答案) |  | |
| 格式 | |||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-02 23:36:39 | ||
图片预览


文档简介
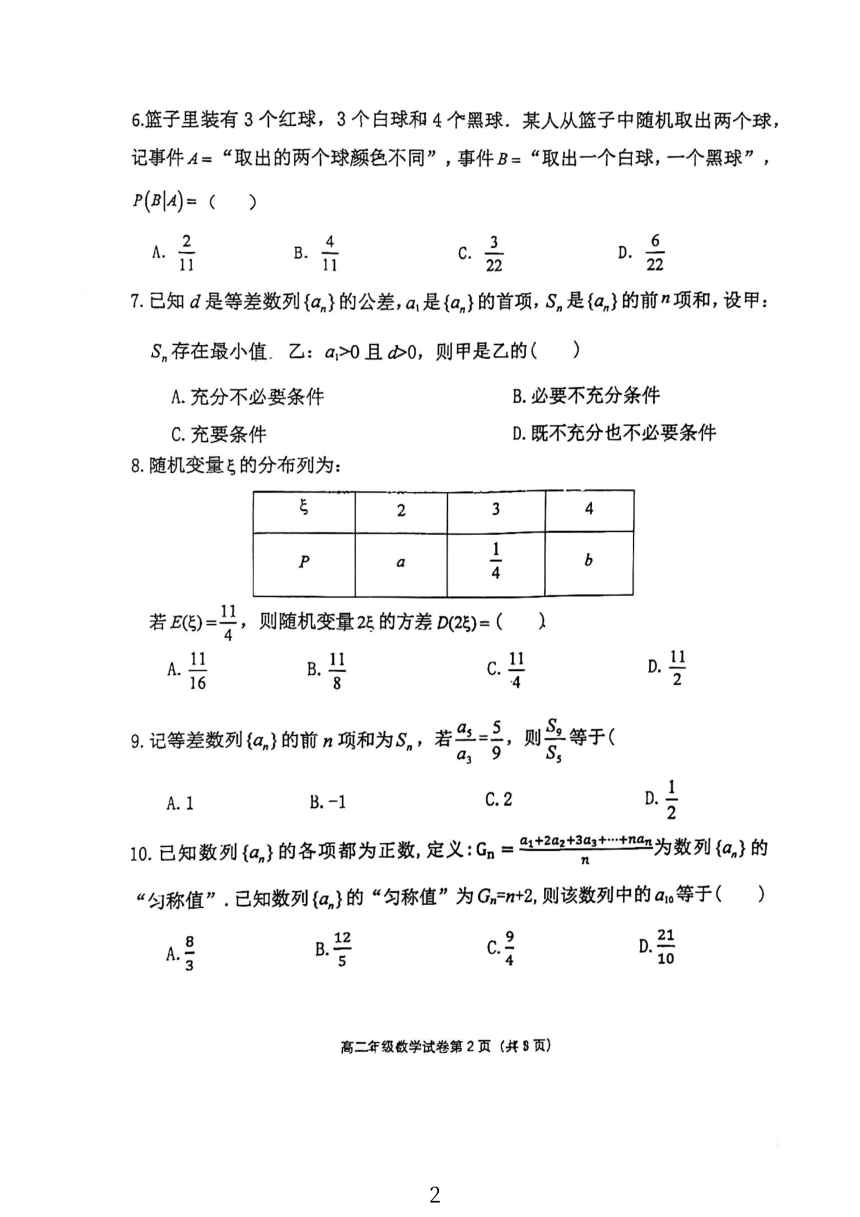
北京市第三十一中学2023一2024学年度第二学期
高二年级数学期中考试试题
2024.4
班级
姓名
学号
成绩
(考试时间120分钟
试卷满分150分)
一、选择题(共10小题,每小题4分,共40分.在每小题列出的四个选项中,
选出符合题目要求的一项)
1.已知数列5,3,√5,√21,3√3…,则9是这个数列的()
A.第12项
B.第13项
C.第14项
D.第15项
2.已知离散型随机变量X服从二项分布X~B(6,p),且E(X)=1,则D()=()
A司
B分
c号
D
3.2022年1月我市某校高三年级1600名学生参加了2022届全市高三期末联考,
己知数学考试成绩X~N100,σ2)(试卷满分150分)。统计结果显示数学考试
成绩在80分到120分之间的人数约为总人数的三,则此次期末联考中成绩不低
于120分的学生人数约为()
A.120
B.160
C.200
D.240
4.在数列{a}中,4=La1=1+
8,则a=(
A.2
B
c
D.8
5.如图,函数y=fx)的图象在点P(2,)处的切线是1,
则f2)+f'(2)=()
A.-4
B.3
C.-2
D.1
高二年级数学试卷第1页(共8页)
1
6篮子里装有3个红球,3个白球和4个黑球.某人从篮子中随机取出两个球,
记事件A=“取出的两个球颜色不同”,事件B=“取出一个白球,一个黑球”,
P(BA4=()
品
B音
c品
7.已知d是等差数列{an}的公差,a,是{an}的首项,Sn是{an}的前n项和,设甲:
Sn存在最小值.乙:a>0且心0,则甲是乙的()
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
8.随机变量5的分布列为:
2
3
4
b
4
若E⑤)-片,则随机变量2左的方差D5)=()
人君
c.1
4
9.记等差数列{a,}的前n项和为3,若=,则9等于(
a39
Ss
A.1
B.-1
C.2
D吃
10.己知数列{a,}的各项都为正数,定义:Gn=+2a2+3a++na为数列{a,}的
“匀称值”.已知数列{an}的“匀称值”为Gn=n+2,则该数列中的ao等于()
A号
B号
c
D
10
高二年级做学试卷第2页(共8页)
2
二、填空题(共5小题,每小题6分,共25分)
11.若2、x、y、z、18成等比数列,则一。
12.若数列a}的通项公式为a,=na=nn∈门,数列6,}的前30项和
Tm=。
13.已知某公路上经过的货车与客车的数量之比为2:1,货车和客车中途停车修
理的概率分别为0.02,0.01,则一辆汽车中途停车修理的概率为。
14.有10件产品,其中3件是次品,从中任取两件,若X表示取得次品的个数,
则P(X<2)=。
15.网络流行语“内卷”,是指一类文化模式达到某种最终形态后,既没办法稳
定下来,也不能转变为新的形态,只能不断地在内部变得更加复杂的现象。数
学中的螺旋线可以形象地展示“内卷”这个词。螺旋线这个词来源于希腊文,
原意是“旋卷”或“缠卷”,如图所示的阴影部分就是一个美丽的旋卷性型的
图案,它的画法是:正方形ABCD的边长为4,取正方形ABCD各边的四等分点E、
F、G、H,作第二个正方形EFGH,然后再取正方形EFGH
各边的四等分点M、N、P、Q,作第三个正方形MNP ,
按此方法继续下去,就可以得到下图。设正方形ABCD的边
长为a1,后续各正方形的边长依次为a2、、…、an、…,
如图阴影部分,设直角三角形AEH面积为,后续各直角
三角形面积依次为2、、…、bn、…,则下列说法正确的是
①正方形MP0的面积为号
②,=4xy
③使不等式b,>成立的正整数n的最大值为4
④数列{bn}的前n项和Sn<4
高二年级数学试卷第3页(共8页)
3
高二年级数学期中考试试题
2024.4
班级
姓名
学号
成绩
(考试时间120分钟
试卷满分150分)
一、选择题(共10小题,每小题4分,共40分.在每小题列出的四个选项中,
选出符合题目要求的一项)
1.已知数列5,3,√5,√21,3√3…,则9是这个数列的()
A.第12项
B.第13项
C.第14项
D.第15项
2.已知离散型随机变量X服从二项分布X~B(6,p),且E(X)=1,则D()=()
A司
B分
c号
D
3.2022年1月我市某校高三年级1600名学生参加了2022届全市高三期末联考,
己知数学考试成绩X~N100,σ2)(试卷满分150分)。统计结果显示数学考试
成绩在80分到120分之间的人数约为总人数的三,则此次期末联考中成绩不低
于120分的学生人数约为()
A.120
B.160
C.200
D.240
4.在数列{a}中,4=La1=1+
8,则a=(
A.2
B
c
D.8
5.如图,函数y=fx)的图象在点P(2,)处的切线是1,
则f2)+f'(2)=()
A.-4
B.3
C.-2
D.1
高二年级数学试卷第1页(共8页)
1
6篮子里装有3个红球,3个白球和4个黑球.某人从篮子中随机取出两个球,
记事件A=“取出的两个球颜色不同”,事件B=“取出一个白球,一个黑球”,
P(BA4=()
品
B音
c品
7.已知d是等差数列{an}的公差,a,是{an}的首项,Sn是{an}的前n项和,设甲:
Sn存在最小值.乙:a>0且心0,则甲是乙的()
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
8.随机变量5的分布列为:
2
3
4
b
4
若E⑤)-片,则随机变量2左的方差D5)=()
人君
c.1
4
9.记等差数列{a,}的前n项和为3,若=,则9等于(
a39
Ss
A.1
B.-1
C.2
D吃
10.己知数列{a,}的各项都为正数,定义:Gn=+2a2+3a++na为数列{a,}的
“匀称值”.已知数列{an}的“匀称值”为Gn=n+2,则该数列中的ao等于()
A号
B号
c
D
10
高二年级做学试卷第2页(共8页)
2
二、填空题(共5小题,每小题6分,共25分)
11.若2、x、y、z、18成等比数列,则一。
12.若数列a}的通项公式为a,=na=nn∈门,数列6,}的前30项和
Tm=。
13.已知某公路上经过的货车与客车的数量之比为2:1,货车和客车中途停车修
理的概率分别为0.02,0.01,则一辆汽车中途停车修理的概率为。
14.有10件产品,其中3件是次品,从中任取两件,若X表示取得次品的个数,
则P(X<2)=。
15.网络流行语“内卷”,是指一类文化模式达到某种最终形态后,既没办法稳
定下来,也不能转变为新的形态,只能不断地在内部变得更加复杂的现象。数
学中的螺旋线可以形象地展示“内卷”这个词。螺旋线这个词来源于希腊文,
原意是“旋卷”或“缠卷”,如图所示的阴影部分就是一个美丽的旋卷性型的
图案,它的画法是:正方形ABCD的边长为4,取正方形ABCD各边的四等分点E、
F、G、H,作第二个正方形EFGH,然后再取正方形EFGH
各边的四等分点M、N、P、Q,作第三个正方形MNP ,
按此方法继续下去,就可以得到下图。设正方形ABCD的边
长为a1,后续各正方形的边长依次为a2、、…、an、…,
如图阴影部分,设直角三角形AEH面积为,后续各直角
三角形面积依次为2、、…、bn、…,则下列说法正确的是
①正方形MP0的面积为号
②,=4xy
③使不等式b,>成立的正整数n的最大值为4
④数列{bn}的前n项和Sn<4
高二年级数学试卷第3页(共8页)
3
同课章节目录
