初中数学华师大版八年级下册19.1矩形练习(含解析)
文档属性
| 名称 | 初中数学华师大版八年级下册19.1矩形练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 183.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-04 07:29:15 | ||
图片预览




文档简介
华师大版第十九章第一节矩形练习
一、单选题
1.下列测量方案中,能确定四边形门框为矩形的是( )
A.测量对角线是否互相平分
B.测量两组对边是否分别相等
C.测量对角线是否相等
D.测量对角线交点到四个顶点的距离是否都相等
2.一个木匠有长的木材,他想用这些木材围绕花园苗床做一个护栏.他为花园苗床设计了如图所示的四种方案,其中不能实现的方案是( )
A. B.
C. D.
3.如图,在矩形ABCD中,AB=8,BC=6,EF经过对角线的交点O,则图中阴影部分的面积是( )
A.6 B.12 C.15 D.24
4.如图,在矩形ABCD中,AD=10,AB=6,E为BC上一点,DE平分∠AEC,则CE的长为( )
A.1 B.2 C.3 D.4
5.如图,将矩形ABCD沿AC折叠,使点B落在点B′处,B′C交AD于点E,若∠l=25°,则∠2等于( )
A.25° B.30° C.50° D.60°
6.如图所示,在矩形纸片 中, ,点 分别是矩形的边 上的动点,将该纸片沿直线 折叠.使点 落在矩形边 上,对应点记为点 ,点 落在 处,连接 与 交于点 .则下列结论成立的是( )
① ;②当点 与点 重合时 ;③ 的面积 的取值范围是 ;④当 时, .
A.①③ B.③④ C.②③ D.②④
二、填空题
7.如图,在矩形ABCD中,∠BOC=120°,则∠BAC= .
8.如图,矩形ABCD中,AB=3cm,BC=4cm,则图中四个小矩形的周长之和为 .
9.七年级某班开展了手工制作竞赛,每个同学都在规定时间内完成一件手工作品.小明同学在制作手工作品的第一、二个步骤是:①先裁下了一张长BC=10cm,宽AB=8cm的长方形纸片ABCD,②将纸片沿着直线AE折叠,点D恰好落在BC边上的F处,则EC的长度为 .
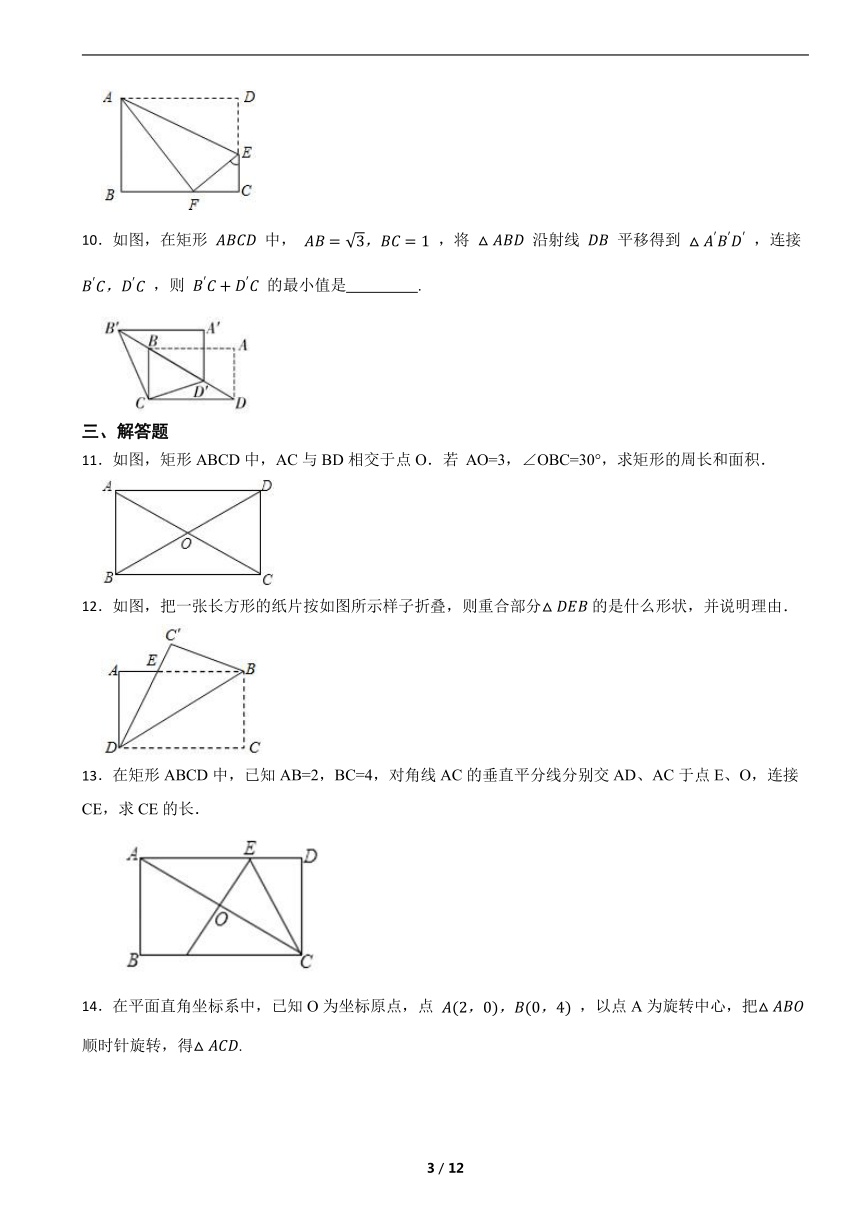
10.如图,在矩形 中, ,将 沿射线 平移得到 ,连接 ,则 的最小值是 .
三、解答题
11.如图,矩形ABCD中,AC与BD相交于点O.若 AO=3,∠OBC=30°,求矩形的周长和面积.
12.如图,把一张长方形的纸片按如图所示样子折叠,则重合部分的是什么形状,并说明理由.
13.在矩形ABCD中,已知AB=2,BC=4,对角线AC的垂直平分线分别交AD、AC于点E、O,连接CE,求CE的长.
14.在平面直角坐标系中,已知O为坐标原点,点 ,以点A为旋转中心,把顺时针旋转,得.
(Ⅰ)如图①,当旋转后满足 轴时,求点C的坐标.
(Ⅱ)如图②,当旋转后点C恰好落在x轴正半轴上时,求点D的坐标.
(Ⅲ)在(Ⅱ)的条件下,边 上的一点P旋转后的对应点为 ,当 取得最小值时,求点P的坐标(直接写出结果即可)
答案解析部分
1.【答案】D
【解析】【解答】解:A、∵对角线互相平分的四边形是平行四边形,而对角线互相平分且相等的四边形才是矩形,
∴选项A不符合题意;
B、∵两组对边分别相等是平行四边形,
∴选项B不符合题意;
C、∵对角线互相平分且相等的四边形才是矩形,
∴对角线相等的四边形不是矩形,
∴选项C不符合题意;
D、∵对角线交点到四个顶点的距离都相等,
∴对角线互相平分且相等,
∵对角线互相平分且相等的四边形是矩形,
∴选项D符合题意.
故答案为:D.
【分析】利用对角线互相平分且相等的四边形是矩形,可作出判断.
2.【答案】D
【解析】【解答】解:A、 花园苗床周长为:(10+6)×2=32m,故此方案能实现,此方案不符合题意;
B、 花园苗床周长为:(10+6)×2=32m,故此方案能实现,此方案不符合题意;
C、花园苗床周长为:(10+6)×2=32m,故此方案能实现,此方案不符合题意;
D、由于垂线段最短,所以平行四边形的另一边长一定大于6m,∴根据平行四边形周长的计算方法可得花园苗床周长一定大于32m,故此方案补能实现,此方案符合题意.
故答案为:D.
【分析】利用平移的思想,A、C选项花园苗床的周长与B选项一样,就是一个长为10m,宽为6m的矩形的周长,从而根据矩形周长计算方法进行计算后可判断A、B、C三选项;D选项中花园苗床的周长就是一个底边为10m,高为6m的平行四边形的周长,根据垂线段最短及平行四边形的周长计算方法进行计算可判断D选项.
3.【答案】B
【解析】【分析】易证△AOE≌△COF,则阴影部分的面积为△CDO的面积,根据矩形对角线分成的四部分面积相等,即可计算阴影部分的面积,即可解题.
【解答】在△AOE和△COF中,
∠EAO=∠FCO,AO=CO,∠COF=∠EOA,
∴△AOE≌△COF,则△AOE和△COF面积相等,
∴阴影部分的面积与△CDO的面积相等,
又∵矩形对角线将矩形分成面积相等的四部分,
∴阴影部分的面积为.
故选B.
【点评】本题考查了矩形对角线相等且互相平分的性质,考查了矩形面积的计算,本题中求证阴影部分的面积与△CDO的面积相等是解题的关键.
4.【答案】B
【解析】【解答】解:∵四边形ABCD是矩形,
∴AD∥BC,
∴∠DEC=∠ADE,
又∵∠DEC=∠AED,
∴∠ADE=∠AED,
∴AE=AD=10,
在直角△ABE中,BE===8,
∴CE=BC﹣BE=AD﹣BE=10﹣8=2.
故答案为:B.
【分析】利用矩形的性质得AD∥BC,利用平行线的性质及角平分线的定义得∠DEC=∠ADE=∠AED,利用等角对等边可求出AE的长,利用勾股定理求出BE的长,然后证明CE=AD﹣BE,代入计算求出CE的长.
5.【答案】C
【解析】【解答】解:由折叠的性质可知:∠ACB′=∠1=25°.
∵四边形ABCD为矩形,
∴AD∥BC,
∴∠2=∠1+∠ACB′=25°+25°=50°.
故答案为:C.
【分析】 由折叠的性质可得∠ACB′=∠1,由矩形的性质可得出AD∥BC,再根据“两直线平行,内错角相等”可求出∠2的度数.
6.【答案】D
【解析】【解答】解:①根据题意可知四边形BFGE为菱形,
∴EF⊥BG且BN=GN,
若BN=AB,则BG=2AB=6,
又∵点E是AD边上的动点,
∴3故①不符合题意;
②如图,过点E作EH⊥BC于点H,则EH=AB=3,
在Rt△ABE中
即
解得:AE= ,
∴BF=DE=6- = .
∴HF= - = .
在Rt△EFH中
= ;
故②符合题意;
③当点E与点A重合时,如图所示, 的面积 有最小值= = ,
当点G与点D重合时 的面积 有最大值= = .
故 < < .
故③不符合题意.
④因为 ,则EG=BF=6- = .根据勾股定理可得ME= ,
∴ .
故④符合题意.
故答案为:D.
【分析】根据矩形的性质、折叠的性质,直角三角形的性质,判断得到答案即可。
7.【答案】60°
【解析】【解答】解:∵四边形ABCD为矩形,
∴∠ABC=90°,BO=CO,
∵∠BOC=120°,
∴∠OBC=∠OCB= =30°,
∴在Rt△ABC中,
∠BAC=180°-90°-30°=60°,
故答案为:60°.
【分析】利用矩形的性质可得∠ABC=90°,BO=CO,根据等边对等角及三角形的内角和定理得出∠OBC=∠OCB=30°,最后根据三角形的内角和定理算出∠BAC的度数.
8.【答案】14cm
【解析】【解答】解:将五个小矩形的所有上边平移至 AD ,所有下边平移至 BC ,所有左边平移至 AB ,所有右边平移至 CD ,
则五个小矩形的周长之和=2(AB+BC)=2×(3+4)=14(cm).
故答案为:14cm.
【分析】运用平移的观点,五个小矩形的上边之和等于 AD ,下边之和等于 BC ,同理,它们的左边之和等于 AB ,右边之和等于 DC ,可知五个小矩形的周长之和为矩形 ABCD 的周长.
9.【答案】3cm
【解析】【解答】解:∵四边形ABCD是矩形,BC=10cm,AB=8cm
∴∠B=∠C=90°,AB=CD=8cm,BC=AD=10cm,
根据翻折的性质可得AF=AD=10cm,EF=DE,
设EC=xcm,则EF=DE=(8-x)cm,
在Rt△ABF中,由勾股定理可得: BF
BF ,
∴CF=BC-BF=10-6=4cm,
在Rt△EFC中,由勾股定理可得:
即 .
解得:
即:EC=3cm
故答案为:3cm
【分析】根据矩形的性质和翻折的性质可得AF=AD=10cm,EF=DE,设EC=xcm,则EF=DE=(8-x)cm,在Rt△ABF中,由勾股定理可得BF的长,进而求得CF的长,在Rt△EFC中,由勾股定理可得关于x的方程,再求解即可。
10.【答案】
【解析】【解答】∵四边形ABCD是矩形,
∴AD=BC=1,∠A=90°,
∴BD= =2,
∵将 沿射线 平移得到 ,
∴ =BD=2,
作点C关于BD的对称点G,连接CG交BD于E,连接 ,
则C = ,CE⊥BD,CG=2CE,
∵CE= ,
∴CG= ,
以 , 为邻边作平行四边形 GH,
则 H= G=C ,
当C、 、H在同一条直线上时,C + H最短,
则 C+ C的最小值=CH,
∵四边形 GH是平行四边形,
∴HG= =2,HG∥ ,
∴HG⊥CG,
∴CH= ,
故答案为: .
【分析】根据题意计算出 =BD=2,作点C关于BD的对称点G,作平行四边形 GH,利用等积法求出CE,进而得到CG,通过当C、 、H在同一条直线上时,C + H最短,可以得到 C+ C的最小值=CH,根据勾股定理可求得结果.
11.【答案】解:∵四边形ABCD是矩形,AO=3,
∴∠ABC=90°,AD=BC,AB=DC,AO=OC,OB=OD,AC=BD,
∴AC=BD=2AO=6,OB=OC,
∴AB= AC=3,
由勾股定理得:BC=3 ,
∴AB=DC=3,AD=BC=3 ,
∴矩形ABCD的周长是AB+BC+CD+AD=6+6 ,
矩形ABCD的面积是AB×BC=3×3 =9
【解析】【分析】根据矩形的性质得出∠ABC=90°,AD=BC,AB=DC,AO=OC,OB=OD,AC=BD,求出AC=BD=2AO=6,OB=OC,求出AB、BC,最后求出周长和面积即可.
12.【答案】解:重合部分是等腰三角形.
由折叠可知, ,
∵四边形ABCD是矩形,
∴AB∥CD
,
,
.
是等腰三角形.
【解析】【分析】根据平行线的性质和翻折的性质求出∠ABD=∠C'DB,得到△BED是等腰三角形.
13.【答案】解:∵四边形ABCD是矩形,
∴AD=BC=4,DC=AB=2,∠D=90°,
∵OE垂直平分AC,
∴EC=AE,
设CE=x,则AE=x,DE=4﹣x,
在△DEC中,由勾股定理得:DE2+DC2=EC2,
即(4﹣x)2+22=x2,
解得:x=,
∴CE的长是.
【解析】【分析】由矩形的性质得出AD=BC=4,DC=AB=2,∠D=90°,由线段垂直平分线的性质得出EC=AE,设CE=x,则AE=x,DE=4﹣x,在△DEC中,由勾股定理得出方程,解方程即可.
14.【答案】A解:(Ⅰ)如图①中,作 轴于H.
∵ ,
∴ ,
∴四边形 是矩形,
∴ ,
∴ ,
∴
(Ⅱ)如图②中,作 于K.
在 中,∵ ,
∴ ,
∵ ,
∴ ,
∴ ,
∴
(Ⅲ)如图③中,连接PA、AP′,作点A关于y轴的对称点A′,连接DA′交y轴于P′,连接AP′.
由题意PA=AP′,
∴AP′+PD=PA+PD,
根据两点之间线段最短,可知当点P与点P′重合时,PA+PD的值最小.
,
∴直线A′D的解析式为 ,
点P坐标
【解析】【分析】(1)证明四边形ADCH为矩形,根据矩形的性质求出答案即可;
(2)作DK⊥AC于K,在直角三角形ADC中,求出DK和AK的值,解出答案即可;
(3)根据题意,由轴对称的性质,结合两点之间线段最短,即当点P和点P'重合时,可得到PA+PD的最小值,求出直线A'D的解析式即可。
1 / 1
一、单选题
1.下列测量方案中,能确定四边形门框为矩形的是( )
A.测量对角线是否互相平分
B.测量两组对边是否分别相等
C.测量对角线是否相等
D.测量对角线交点到四个顶点的距离是否都相等
2.一个木匠有长的木材,他想用这些木材围绕花园苗床做一个护栏.他为花园苗床设计了如图所示的四种方案,其中不能实现的方案是( )
A. B.
C. D.
3.如图,在矩形ABCD中,AB=8,BC=6,EF经过对角线的交点O,则图中阴影部分的面积是( )
A.6 B.12 C.15 D.24
4.如图,在矩形ABCD中,AD=10,AB=6,E为BC上一点,DE平分∠AEC,则CE的长为( )
A.1 B.2 C.3 D.4
5.如图,将矩形ABCD沿AC折叠,使点B落在点B′处,B′C交AD于点E,若∠l=25°,则∠2等于( )
A.25° B.30° C.50° D.60°
6.如图所示,在矩形纸片 中, ,点 分别是矩形的边 上的动点,将该纸片沿直线 折叠.使点 落在矩形边 上,对应点记为点 ,点 落在 处,连接 与 交于点 .则下列结论成立的是( )
① ;②当点 与点 重合时 ;③ 的面积 的取值范围是 ;④当 时, .
A.①③ B.③④ C.②③ D.②④
二、填空题
7.如图,在矩形ABCD中,∠BOC=120°,则∠BAC= .
8.如图,矩形ABCD中,AB=3cm,BC=4cm,则图中四个小矩形的周长之和为 .
9.七年级某班开展了手工制作竞赛,每个同学都在规定时间内完成一件手工作品.小明同学在制作手工作品的第一、二个步骤是:①先裁下了一张长BC=10cm,宽AB=8cm的长方形纸片ABCD,②将纸片沿着直线AE折叠,点D恰好落在BC边上的F处,则EC的长度为 .
10.如图,在矩形 中, ,将 沿射线 平移得到 ,连接 ,则 的最小值是 .
三、解答题
11.如图,矩形ABCD中,AC与BD相交于点O.若 AO=3,∠OBC=30°,求矩形的周长和面积.
12.如图,把一张长方形的纸片按如图所示样子折叠,则重合部分的是什么形状,并说明理由.
13.在矩形ABCD中,已知AB=2,BC=4,对角线AC的垂直平分线分别交AD、AC于点E、O,连接CE,求CE的长.
14.在平面直角坐标系中,已知O为坐标原点,点 ,以点A为旋转中心,把顺时针旋转,得.
(Ⅰ)如图①,当旋转后满足 轴时,求点C的坐标.
(Ⅱ)如图②,当旋转后点C恰好落在x轴正半轴上时,求点D的坐标.
(Ⅲ)在(Ⅱ)的条件下,边 上的一点P旋转后的对应点为 ,当 取得最小值时,求点P的坐标(直接写出结果即可)
答案解析部分
1.【答案】D
【解析】【解答】解:A、∵对角线互相平分的四边形是平行四边形,而对角线互相平分且相等的四边形才是矩形,
∴选项A不符合题意;
B、∵两组对边分别相等是平行四边形,
∴选项B不符合题意;
C、∵对角线互相平分且相等的四边形才是矩形,
∴对角线相等的四边形不是矩形,
∴选项C不符合题意;
D、∵对角线交点到四个顶点的距离都相等,
∴对角线互相平分且相等,
∵对角线互相平分且相等的四边形是矩形,
∴选项D符合题意.
故答案为:D.
【分析】利用对角线互相平分且相等的四边形是矩形,可作出判断.
2.【答案】D
【解析】【解答】解:A、 花园苗床周长为:(10+6)×2=32m,故此方案能实现,此方案不符合题意;
B、 花园苗床周长为:(10+6)×2=32m,故此方案能实现,此方案不符合题意;
C、花园苗床周长为:(10+6)×2=32m,故此方案能实现,此方案不符合题意;
D、由于垂线段最短,所以平行四边形的另一边长一定大于6m,∴根据平行四边形周长的计算方法可得花园苗床周长一定大于32m,故此方案补能实现,此方案符合题意.
故答案为:D.
【分析】利用平移的思想,A、C选项花园苗床的周长与B选项一样,就是一个长为10m,宽为6m的矩形的周长,从而根据矩形周长计算方法进行计算后可判断A、B、C三选项;D选项中花园苗床的周长就是一个底边为10m,高为6m的平行四边形的周长,根据垂线段最短及平行四边形的周长计算方法进行计算可判断D选项.
3.【答案】B
【解析】【分析】易证△AOE≌△COF,则阴影部分的面积为△CDO的面积,根据矩形对角线分成的四部分面积相等,即可计算阴影部分的面积,即可解题.
【解答】在△AOE和△COF中,
∠EAO=∠FCO,AO=CO,∠COF=∠EOA,
∴△AOE≌△COF,则△AOE和△COF面积相等,
∴阴影部分的面积与△CDO的面积相等,
又∵矩形对角线将矩形分成面积相等的四部分,
∴阴影部分的面积为.
故选B.
【点评】本题考查了矩形对角线相等且互相平分的性质,考查了矩形面积的计算,本题中求证阴影部分的面积与△CDO的面积相等是解题的关键.
4.【答案】B
【解析】【解答】解:∵四边形ABCD是矩形,
∴AD∥BC,
∴∠DEC=∠ADE,
又∵∠DEC=∠AED,
∴∠ADE=∠AED,
∴AE=AD=10,
在直角△ABE中,BE===8,
∴CE=BC﹣BE=AD﹣BE=10﹣8=2.
故答案为:B.
【分析】利用矩形的性质得AD∥BC,利用平行线的性质及角平分线的定义得∠DEC=∠ADE=∠AED,利用等角对等边可求出AE的长,利用勾股定理求出BE的长,然后证明CE=AD﹣BE,代入计算求出CE的长.
5.【答案】C
【解析】【解答】解:由折叠的性质可知:∠ACB′=∠1=25°.
∵四边形ABCD为矩形,
∴AD∥BC,
∴∠2=∠1+∠ACB′=25°+25°=50°.
故答案为:C.
【分析】 由折叠的性质可得∠ACB′=∠1,由矩形的性质可得出AD∥BC,再根据“两直线平行,内错角相等”可求出∠2的度数.
6.【答案】D
【解析】【解答】解:①根据题意可知四边形BFGE为菱形,
∴EF⊥BG且BN=GN,
若BN=AB,则BG=2AB=6,
又∵点E是AD边上的动点,
∴3
②如图,过点E作EH⊥BC于点H,则EH=AB=3,
在Rt△ABE中
即
解得:AE= ,
∴BF=DE=6- = .
∴HF= - = .
在Rt△EFH中
= ;
故②符合题意;
③当点E与点A重合时,如图所示, 的面积 有最小值= = ,
当点G与点D重合时 的面积 有最大值= = .
故 < < .
故③不符合题意.
④因为 ,则EG=BF=6- = .根据勾股定理可得ME= ,
∴ .
故④符合题意.
故答案为:D.
【分析】根据矩形的性质、折叠的性质,直角三角形的性质,判断得到答案即可。
7.【答案】60°
【解析】【解答】解:∵四边形ABCD为矩形,
∴∠ABC=90°,BO=CO,
∵∠BOC=120°,
∴∠OBC=∠OCB= =30°,
∴在Rt△ABC中,
∠BAC=180°-90°-30°=60°,
故答案为:60°.
【分析】利用矩形的性质可得∠ABC=90°,BO=CO,根据等边对等角及三角形的内角和定理得出∠OBC=∠OCB=30°,最后根据三角形的内角和定理算出∠BAC的度数.
8.【答案】14cm
【解析】【解答】解:将五个小矩形的所有上边平移至 AD ,所有下边平移至 BC ,所有左边平移至 AB ,所有右边平移至 CD ,
则五个小矩形的周长之和=2(AB+BC)=2×(3+4)=14(cm).
故答案为:14cm.
【分析】运用平移的观点,五个小矩形的上边之和等于 AD ,下边之和等于 BC ,同理,它们的左边之和等于 AB ,右边之和等于 DC ,可知五个小矩形的周长之和为矩形 ABCD 的周长.
9.【答案】3cm
【解析】【解答】解:∵四边形ABCD是矩形,BC=10cm,AB=8cm
∴∠B=∠C=90°,AB=CD=8cm,BC=AD=10cm,
根据翻折的性质可得AF=AD=10cm,EF=DE,
设EC=xcm,则EF=DE=(8-x)cm,
在Rt△ABF中,由勾股定理可得: BF
BF ,
∴CF=BC-BF=10-6=4cm,
在Rt△EFC中,由勾股定理可得:
即 .
解得:
即:EC=3cm
故答案为:3cm
【分析】根据矩形的性质和翻折的性质可得AF=AD=10cm,EF=DE,设EC=xcm,则EF=DE=(8-x)cm,在Rt△ABF中,由勾股定理可得BF的长,进而求得CF的长,在Rt△EFC中,由勾股定理可得关于x的方程,再求解即可。
10.【答案】
【解析】【解答】∵四边形ABCD是矩形,
∴AD=BC=1,∠A=90°,
∴BD= =2,
∵将 沿射线 平移得到 ,
∴ =BD=2,
作点C关于BD的对称点G,连接CG交BD于E,连接 ,
则C = ,CE⊥BD,CG=2CE,
∵CE= ,
∴CG= ,
以 , 为邻边作平行四边形 GH,
则 H= G=C ,
当C、 、H在同一条直线上时,C + H最短,
则 C+ C的最小值=CH,
∵四边形 GH是平行四边形,
∴HG= =2,HG∥ ,
∴HG⊥CG,
∴CH= ,
故答案为: .
【分析】根据题意计算出 =BD=2,作点C关于BD的对称点G,作平行四边形 GH,利用等积法求出CE,进而得到CG,通过当C、 、H在同一条直线上时,C + H最短,可以得到 C+ C的最小值=CH,根据勾股定理可求得结果.
11.【答案】解:∵四边形ABCD是矩形,AO=3,
∴∠ABC=90°,AD=BC,AB=DC,AO=OC,OB=OD,AC=BD,
∴AC=BD=2AO=6,OB=OC,
∴AB= AC=3,
由勾股定理得:BC=3 ,
∴AB=DC=3,AD=BC=3 ,
∴矩形ABCD的周长是AB+BC+CD+AD=6+6 ,
矩形ABCD的面积是AB×BC=3×3 =9
【解析】【分析】根据矩形的性质得出∠ABC=90°,AD=BC,AB=DC,AO=OC,OB=OD,AC=BD,求出AC=BD=2AO=6,OB=OC,求出AB、BC,最后求出周长和面积即可.
12.【答案】解:重合部分是等腰三角形.
由折叠可知, ,
∵四边形ABCD是矩形,
∴AB∥CD
,
,
.
是等腰三角形.
【解析】【分析】根据平行线的性质和翻折的性质求出∠ABD=∠C'DB,得到△BED是等腰三角形.
13.【答案】解:∵四边形ABCD是矩形,
∴AD=BC=4,DC=AB=2,∠D=90°,
∵OE垂直平分AC,
∴EC=AE,
设CE=x,则AE=x,DE=4﹣x,
在△DEC中,由勾股定理得:DE2+DC2=EC2,
即(4﹣x)2+22=x2,
解得:x=,
∴CE的长是.
【解析】【分析】由矩形的性质得出AD=BC=4,DC=AB=2,∠D=90°,由线段垂直平分线的性质得出EC=AE,设CE=x,则AE=x,DE=4﹣x,在△DEC中,由勾股定理得出方程,解方程即可.
14.【答案】A解:(Ⅰ)如图①中,作 轴于H.
∵ ,
∴ ,
∴四边形 是矩形,
∴ ,
∴ ,
∴
(Ⅱ)如图②中,作 于K.
在 中,∵ ,
∴ ,
∵ ,
∴ ,
∴ ,
∴
(Ⅲ)如图③中,连接PA、AP′,作点A关于y轴的对称点A′,连接DA′交y轴于P′,连接AP′.
由题意PA=AP′,
∴AP′+PD=PA+PD,
根据两点之间线段最短,可知当点P与点P′重合时,PA+PD的值最小.
,
∴直线A′D的解析式为 ,
点P坐标
【解析】【分析】(1)证明四边形ADCH为矩形,根据矩形的性质求出答案即可;
(2)作DK⊥AC于K,在直角三角形ADC中,求出DK和AK的值,解出答案即可;
(3)根据题意,由轴对称的性质,结合两点之间线段最短,即当点P和点P'重合时,可得到PA+PD的最小值,求出直线A'D的解析式即可。
1 / 1
