专题05 四边形的性质与判定 课件(共62张PPT)-2024年中考数学二轮复习讲练测(全国通用)
文档属性
| 名称 | 专题05 四边形的性质与判定 课件(共62张PPT)-2024年中考数学二轮复习讲练测(全国通用) |

|
|
| 格式 | pptx | ||
| 文件大小 | 31.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-03 00:00:00 | ||
图片预览









文档简介
(共62张PPT)
专题05 四边形的性质与判定
2024年中考数学二轮复习讲练测
目录
CONTENTS
01
02
知识建构
03
考点精讲
考情分析
第一部分
考情分析
02
考点要求 命题预测
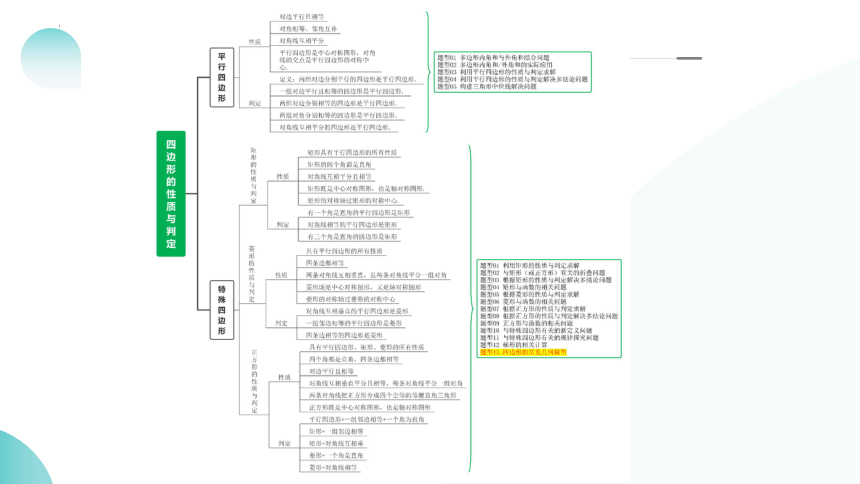
平行四边形 平行四边形和特殊平行四边形在中考数学中是占比比较大的一块考点,考察内容主要有各个特殊四边形的性质、判定、以及其应用:考察题型上从选择到填空再都解答题都有,题型变化也比较多样;并且考察难度也都是中等和中等偏上,难度较大,综合性比较强.所以需要考生在复习这块内容的时候一定要准确掌握其性质与判定,并且会在不同的结合问题上注意和其他考点的融合.平行四边形与特殊平行四边形的考察热点有:多边形内角和定理、平行四边形的性质与判定定理、平行四边形的综合应用;矩形、菱形、正方形的性质与判定定理;特殊四边形的图形平移、轴对称、旋转等结合问题.
特殊四边形
第二部分
知识建构
稿定PPT
稿定PPT,海量素材持续更新,上千款模板选择总有一款适合你
02
第三部分
考点精讲
题型01 多边形内角和与外角和综合问题
考点一 平行四边形
多边形的有关计算公式有很多,一定要牢记,代错公式容易导致错误:
①n边形内角和=(n-2)×180°(n≥3).
②从n边形的一个顶点可以引出(n-3)条对角线,n个顶点可以引出n(n-3)条对角线,但是每条对角线计算了两次,因此n边形共有 条对角线.
③n边形的边数=(内角和÷180°)+2.
④n边形的外角和是360°.
⑤n边形的外角和加内角和=n×180°.
⑥在n边形内任取一点O,连接O与各个顶点,把n边形分成n个三角形;在n边形的任意一边上任取一点O,连接O点与其不相邻的其它各顶点的线段可以把n边形分成(n-1)个三角形;连接n边形的任一顶点A与其不相邻的各个顶点的线段,把n边形分成(n-2)个三角形.
易错点拨
题型01 多边形内角和与外角和综合问题
1)n边形的内角和随边数的增加而增加,边数每增加1,内角和增加180°.
2)任意多边形的内角和均为180°的整数倍.
3)利用多边形内角和定理可解决三类问题:①已知多边形的边数求内角和;②已知多边形的内角和求边数;③已知足够的角度条件下求某一个内角的度数.
4)任意多边形的外角和等于360°,与多边形的形状和边数无关.
5)正n边形的每个内角为,每一个外角为.
6)正n边形有n条对称轴.
7)对于正n边形,当n为奇数时,是轴对称图形;当n为偶数时,既是轴对称图形,又是中心对称图形.
提分笔记
1.(2023·山东枣庄·中考真题)如图,一束太阳光线平行照射在放置于地面的正六边形上,若,则的度数为( )
A. B. C. D.
【详解】解:如图:∵正六边形的一个外角的度数为:,
∴正六边形的一个内角的度数为:,即:,
∵一束太阳光线平行照射在放置于地面的正六边形上,,∴,
∴,∴;故选B.
2.(2023·新疆·中考真题)一个多边形的每个内角都是,这个多边形是 边形.
【详解】解:∵该多边形每个内角都是,∴该多边形为正多边形,
∴该多边形一个外角,∴该多边形的边数,故答案为:十.
题型01 多边形内角和与外角和综合问题
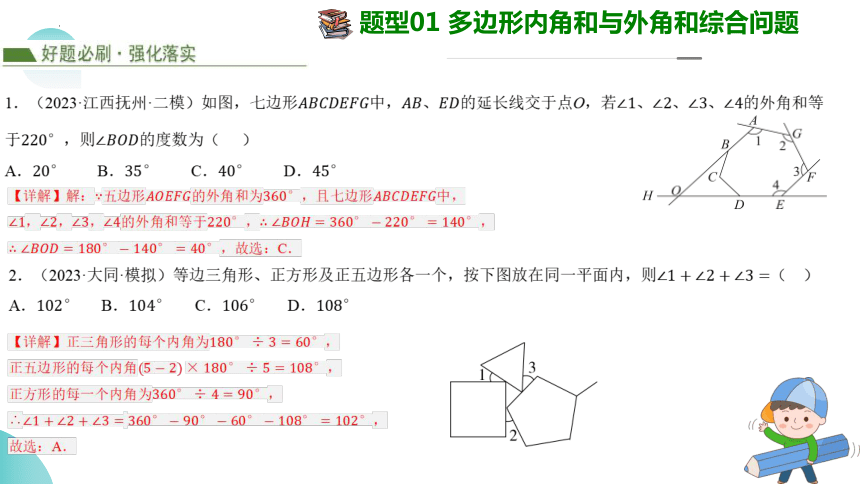
1.(2023·江西抚州·二模)如图,七边形中,、的延长线交于点O,若、、、的外角和等于,则的度数为( )
A. B. C. D.
【详解】解:五边形的外角和为,且七边形中,
,,,的外角和等于,,
,故选:C.
2.(2023·大同·模拟)等边三角形、正方形及正五边形各一个,按下图放在同一平面内,则( )
A. B. C. D.
【详解】正三角形的每个内角为,
正五边形的每个内角,
正方形的每一个内角为,
∴ ,
故选:A.
题型01 多边形内角和与外角和综合问题
题型02 多边形内角和/外角和的实际应用
1.(2020·山东德州·中考真题)如图,小明从A点出发,沿直线前进8米后向左转45°,再沿直线前进8米,又向左转45°……照这样走下去,他第一次回到出发点A时,共走路程为( )
A.80米 B.96米 C.64米 D.48米
题型02 多边形内角和/外角和的实际应用
2.(2021·江苏镇江·中考真题)如图,花瓣图案中的正六边形ABCDEF的每个内角的度数是 .
【详解】解:设这个正六边形的每一个内角的度数为x,
则6x=(6﹣2) 180°,
解得x=120°.
故答案为:120°.
题型03 利用平行四边形的性质与判定求解
平行四边形的性质:1)对边平行且相等; 2)对角相等、邻角互补; 3)对角线互相平分;
4)平行四边形是中心对称图形,但不是轴对称图形,平行四边形的对角线的交点是平行四边形的对称中心.
【解题技巧】
1)平行四边形相邻两边之和等于周长的一半.
2)平行四边形中有相等的边、角和平行关系,所以经常需结合三角形全等来解题.
3)过平行四边形对称中心的任一直线等分平行四边形的面积及周长.
4)如图①,AE平分∠BAD,则可利用平行线的性质结合等角对等边得到△ABE为等腰三角形,即AB=BE.
5)如图②,已知点E为AD上一点,根据平行线间的距离处处相等,可得S△BEC=S△ABE+S△CDE.
6)如图③,根据平行四边形的面积的求法,可得AE·BC=AF·CD.
解题大招
平行四边形的判定定理:
①定义:两组对边分别平行的四边形是平行四边形.
②一组对边平行且相等的四边形是平行四边形.
③两组对边分别相等的四边形是平行四边形.
④两组对角分别相等的四边形是平行四边形.
⑤对角线互相平分的四边形是平行四边形.
【解题技巧】
一般地,要判定一个四边形是平行四边形有多种方法,主要有以下三种思路:
1)当已知条件中有关于所证四边形的角时,可用“两组对角分别相等的四边形是平行四边形”来证明;
2)当已知条件中有关于所证四边形的边时,可选择“两组对边分别相等的四边形是平行四边形”或“两组对边分别平行的四边形是平行四边形”或“有一组对边平行且相等的四边形是平行四边形”来证明;
3)当已知条件中有关于所证四边形的对角线时,可选择“对角线互相平分的四边形是平行四边形”来证明.
题型03 利用平行四边形的性质与判定求解
解题大招
1.(2023·浙江湖州·中考真题)如图,已知,以点O为圆心,适当长为半径作圆弧,与角的两边分别交于C,D两点,分别以点C,D为圆心,大于长为半径作圆弧,两条圆弧交于内一点P,连接,过点P作直线,交OB于点E,过点P作直线,交于点F.若,,则四边形的面积是( )
A. B. C. D.
【详解】解:过P作于M,由作图得:平分,∴,∴,∴,
∵,,∴四边形为平行四边形,,∴,∴,
设,在中,,即:,解得:,
∴.故选:B.
题型03 利用平行四边形的性质与判定求解
2.(2023·辽宁·中考真题)如图,平行四边形的对角线,相交于点,过点作,交的延长线于点,连接,交于点,则四边形的面积与的面积的比值为 .
【详解】解:∵四边形是平行四边形,∴,,又∵,∴四边形是平行四边形,,∴,
∵,∴,,∴,∴,,∴,,∴同理,∵,∴,
设,则,,
∴∴,故答案为∶
1.(2024·陕西西安·模拟预测)如图, 菱形中, 对角线交于点O,, 垂足为点H,
分别交及的延长线于点E、M、F,且,则的值为( )
A. B. C. D.
【详解】解:∵四边形是菱形,∴,,,∵,∴,∴四边形是平行四边形,∴,∵,∴,∴,∴,
∵∴,∴,∴,故选:D.
题型03 利用平行四边形的性质与判定求解
题型04 利用平行四边形的性质与判定解决多结论问题
1.(2022·山东泰安·中考真题)如图,平行四边形的对角线,相交于点O.点E为的中点,连接并延长交于点F,,.下列结论:①;②;③四边形是菱形;④.
其中正确结论的个数是( )A.4 B.3 C.2 D.1
1.(2023·辽宁抚顺·二模)如图,在平行四边形中,,E,F分别是上的动点,且,连接,与相交于P,过点P作,交于M,交于N,当E,F在上移动时,下列结论:①;②;③;④.其中正确的有 .(填序号)
【详解】解:∵平行四边形中,,∴,,∴,∵,∴,∴,故①正确;∴,故②正确;∵,∴与之间的距离相等,∴,故④正确;
∵,即,∵,∴,,∴,,∴,
∴,故③正确;综上,①②③④都正确,
题型04 利用平行四边形的性质与判定解决多结论问题
题型05 构建三角形中位线解决问题
构造三角形中位线的常用方法:
1)连接两点构造三角形中位线;
2) 已知中点,取另一条线段的中点构造中位线.
3) 利用角平分线+垂直构造三角形的中位线.
高分秘籍
1.(2023·广西·中考真题)如图,在边长为2的正方形中,E,F分别是上的动点,M,N分别是的中点,则的最大值为 .
【详解】如图所示,连接,
∵M,N分别是的中点,∴是的中位线,∴,
∵四边形是正方形,∴,∴,
∴当最大时,最大,此时最大,
∵点E是上的动点,∴当点E和点C重合时,最大,即的长度,
∴此时,∴,∴的最大值为.
2.(2021·天津·中考真题)如图,正方形的边长为4,对角线相交于点O,点E,F分别在的延长线上,且,G为的中点,连接,交于点H,连接,则的长为 .
【详解】解:如图,作OK⊥BC,垂足为点K,
∵正方形边长为4,∴OK=2,KC=2,∴KC=CE,∴CH是△OKE的中位线
∴,作GM⊥CD,垂足为点M,
∵G点为EF中点,∴GM是△FCE的中位线,
∴,,
∴,
在Rt△MHG中,,
故答案为:.
题型05 构建三角形中位线解决问题
1.(2023·山东青岛·模拟预测)如图,四边形顶点是四边形各边中点,若把涂满红油漆需要桶,那么要把其余部分涂满黑颜色,需要 桶
【详解】解:如图所示,连接,∵分别是的中点,∴,
∴∴,同理可得,
则同理可得∴
若把涂满红油漆需要桶,那么要把其余部分涂满黑颜色,需要桶,故答案为:.
题型05 构建三角形中位线解决问题
2.(2023·安徽·二模)如图,在中,,延长到点D,,点E是的中点,交于点F,则的面积为 .
【详解】解:∵,,∴,
∵点E是的中点,∴,取的中点,连接,则:,
∴,∴,∴,
∴,∴;故答案为:.
考点二 特殊四边形
1. 平行四边形、矩形、菱形、正方形之间的关系:
2. 平行四边形、矩形、菱形、正方形的性质
考点二 特殊四边形
3 平行四边形、矩形、菱形、正方形的判定
查漏补缺
题型01 利用矩形的性质与判定求解
矩形的定义:有一个角是直角的平行四边形叫做矩形.
矩形的性质:1)矩形具有平行四边形的所有性质;
2)矩形的四个角都是直角;
3)对角线互相平分且相等;
4)矩形既是中心对称图形,也是轴对称图形.
矩形的对称中心是矩形对角线的交点;
矩形有两条对称轴,矩形的对称轴是过矩形对边中点的直线;
矩形的对称轴过矩形的对称中心.
【推论】1)在直角三角形中斜边的中线,等于斜边的一半.
2)直角三角形中,30度角所对应的直角边等于斜边的一半.
矩形的判定:1) 有一个角是直角的平行四边形是矩形;
2)对角线相等的平行四边形是矩形;
3)有三个角是直角的四边形是矩形.
【解题思路】要证明一个四边形是矩形,首先要判断四边形是否为平行四边形,
若是,则需要再证明对角线相等或有一个角是直角;若不易判断,则可通过证明有三个角是直角来直接证明.
提分笔记
易混易错
1. 对于矩形的定义要注意两点:
a.是平行四边形;
b.有一个角是直角.
2. 定义说有一个角是直角的平行四边形才是矩形,
不要错误地理解为有一个角是直角的四边形是矩形.
1.(2023·四川雅安·中考真题)如图,在中,.P为边上一动点,作于点D,于点E,则的最小值为 .
【详解】解:如图,连接,∵,∴,
∵于点D,于点E,,∴四边形是矩形,
∴,由垂线段最短可得时,线段的值最小,此时线段的值最小,
此时,,代入数据:,∴,∴的最小值为,故答案为:.
题型01 利用矩形的性质与判定求解
2.(2022·内蒙古鄂尔多斯·中考真题)如图,菱形ABCD中,AB=2,∠ABC=60°,矩形BEFG的边EF经过点C,且点G在边AD上,若BG=4,则BE的长为( )A. B. C. D.3
【详解】解:过点G作GM⊥BC于点M,过点C作CN⊥AD于点N,
∵四边形ABCD为菱形,∴AB=BC=CD=,AD=BC,∠ABC=∠D=60°,AD∥BC,
∴∠MGN=90°,∴四边形GMCN为矩形,∴GM=CN,
在△CDN中,∠D=60°,CD=,∴CN=CD sin60°=,∴MG=3,
∵四边形BEFG为矩形,∴∠E=90°,BG∥EF,∴∠BCE=∠GBM,
又∵∠E=∠BMG,∴△GBM∽△BCE,∴,∴,∴BE= ,故选:B.
1.(2024·山西朔州·一模)如图,在矩形中,为对角线上的一点(不与点重合),连接,过点作交边于点,连接.若,则的长为 .
【详解】解:过点作于,延长交于,则,如图:
四边形为矩形,,,,
四边形为矩形,,,,
, ,
, , ,,
, ,
,,,
,,
,, ,即:,解得:,
,
故答案为:.
题型01 利用矩形的性质与判定求解
题型02 与矩形(或正方形)有关的折叠问题
矩形的折叠问题的常用解题思路:
1)对折叠前后的图形进行细致分析,折叠后的图形与原图形全等,对应边、对应角分别相等,找出各相等的边或角;
2)折痕可看作角平分线(对称线段所在的直线与折痕的夹角相等).
3) 折痕可看作垂直平分线(互相重合的两点之间的连线被折痕垂直平分).
4)选择一个直角三角形(不找以折痕为边长的直角三角形),利用未知数表示其它直角三角形三边,通过勾股定理/相似三角形知识求解.
解题大招
1.(2023·黑龙江牡丹江·中考真题)在以“矩形的折叠”为主题的数学活动课上,某位同学进行了如下操作:
第一步:将矩形纸片的一端,利用图①的方法折出一个正方形,然后把纸片展平;
第二步:将图①中的矩形纸片折叠,使点C恰好落在点F处,得到折痕,如图②.
根据以上的操作,若,,则线段的长是( )
A.3 B. C.2 D.1
【详解】解:如图,过点作,交于点,
在和中,
设,则,
,即:,解得:,
,, ,,,
,故选:C.
题型02 与矩形(或正方形)有关的折叠问题
1.(2024·贵州贵阳·模拟预测)如图,在矩形中,,将矩形沿折叠,使点与点重合.
(1)若,求的度数;
(2)求证:;
(3)若,,求的长.
【详解】(1)解:∵四边形是矩形,∴,
由翻折可知: ,∴,∴度数为;
(2)证明:∵四边形是矩形,∴, 由翻折可知: ,,∴,,在和中,,∴;
题型02 与矩形(或正方形)有关的折叠问题
(3)解:设,则,
∵沿翻折后点与点重合,∴,
在中,由勾股定理得,即 ,
解得,∴.
题型03 根据矩形的性质与判定解决多结论问题
1.(2021·山东泰安·中考真题)如图,在平行四边形中,E是的中点,则下列四个结论:①;②若,,则;③若,则;④若,则与全等.其中正确结论的个数为( )A.1个 B.2个 C.3个 D.4个
【详解】解:∵平行四边形中,E是的中点,∴,,,∴,,
∴,∴,∴,故①正确;若,则平行四边形是矩形,由矩形的对角线相等,而点E是矩形的对角线的交点可知,E点到B、C两点的距离相等,∴E点在BC的垂直平分线上,由,可得BN=CN,所以N点是BC的中点,∴MN垂直平分BC,∴,故②正确;若,则BN=2CN,如图1,分别过D、E两点向BC作垂线,垂足分别为Q点和P点,∵E点是BD中点,∴DQ=2EP,∵,∴,故③正确;若,因为,所以,分别过N、C两点向AD作垂线,垂足分别为H、K,由平行线间的距离处处相等可知:NH=CK,∴,∴,∴,∴,又∵,∴,故④正确;故选:D.
(2022·湖南娄底·统考模拟预测)如图,在矩形ABCD中,DE平分交BC于点E,点F是CD边上一点(不与点D重合).点P为DE上一动点,,将绕点P逆时针旋转90°后,角的两边交射线DA于H,G两点,有下列结论:①;②;③;④,其中一定正确的是( )
A.①② B.②③ C.①④ D.③④
【详解】解:根据旋转的性质可知,,
∵DE平分,∴,∴,∴PH=PD,
∵∴
在和中,∵∴∴
∵∴∴故③正确;
∵,∴∴
即,故④正确;
根据已知条件无法证明①DH=DE,②DP=DG.故选:D.
题型03 根据矩形的性质与判定解决多结论问题
题型04 矩形与函数的相关问题
1.(2023·陕西·中考真题)如图,在矩形和正方形中,点A在y轴正半轴上,点C,F均在x轴正半轴上,点D在边上,,.若点B,E在同一个反比例函数的图象上,则这个反比例函数的表达式是 .
【详解】解:∵四边形是矩形,∴,
设正方形的边长为m,∴,
∵,∴,∴,,
设反比例函数的表达式为,∴,
解得或(不合题意,舍去),
∴,∴,∴这个反比例函数的表达式是,
故答案为:.
1.(2022·陕西西安·模拟预测)如图,一次函数的图象交轴于点,交轴于点,点在线段上不与点,重合,过点分别作和的垂线,垂足为,.当矩形的面积为时,点的坐标为( )
A., B. C.,或 D.,或,)
【详解】解:点在线段上不与点,重合,且直线的解析式为,
设点的坐标为,,
,.
矩形的面积为,
,
,,
点的坐标为,或,.
故选:D.
题型04 矩形与函数的相关问题
题型05 根据菱形的性质与判定求解
菱形的性质:
1)具有平行四边形的所有性质;
2)四条边都相等;
3)两条对角线互相垂直,且每条对角线平分一组对角.
4)菱形既是中心对称图形,又是轴对称图形,
菱形的对称中心是菱形对角线的交点,
菱形的对称轴是菱形对角线所在的直线,
菱形的对称轴过菱形的对称中心.
菱形的判定:
1)对角线互相垂直的平行四边形是菱形.
2)一组邻边相等的平行四边形是菱形.
3)四条边相等的四边形是菱形.
【解题思路】判定一个四边形是菱形时,可先说明它是平行四边形,
再说明它的一组邻边相等或它的对角线互相垂直,也可直接说明它的四条边都相等或它的对角线互相垂直平分.
菱形的面积公式:S=ah=对角线乘积的一半(其中a为边长,h为高).
菱形的周长公式:周长l=4a(其中a为边长).
提分笔记
易错点拨
1. 对于菱形的定义要注意两点:
a.是平行四边形;
b.一组邻边相等.
2. 定义说有一组邻边相等的平行四边形才是菱形,不要错误地理解为有一组邻边相等的四边形是菱形.
3. 菱形的面积S=对角线乘积的一半,适用于对角线互相垂直的任意四边形的面积的计算.
4. 在求菱形面积时,要根据图形特点及已知条体灵活选择面积公式来解决问题,
5. 在利用对角线长求菱形的面积时,要特别注意不要漏掉计算公式中的 .
(2022·江苏连云港·统考中考真题)如图,四边形为平行四边形,延长到点,使,且.
(1)求证:四边形为菱形;
(2)若是边长为2的等边三角形,点、、分别在线段、、上运动,求的最小值.
【详解】(1)证明:∵四边形是平行四边形,∴,,
∵,∴,又∵点在的延长线上,
∴,∴四边形为平行四边形,
又∵,∴四边形为菱形.
题型05 根据菱形的性质与判定求解
(2)解:如图,由菱形对称性得,点关于的对称点在上,∴,
当、、共线时,,
过点作,垂足为,
∵,∴的最小值即为平行线间的距离的长,
∵是边长为2的等边三角形,∴在中,,,,
∴,∴的最小值为.
1.(2023·湖南株洲·模拟预测)如图,菱形ABCD的对角线AC与BD相交于点O,E为AD的中点,连接OE,,,则( )
A.4 B. C.2 D.
【详解】是菱形,E为AD的中点,
,.
是直角三角形,.
,,
,.
,即,
,.
故选:C.
题型05 根据菱形的性质与判定求解
题型06 菱形与函数的相关问题
1.(2023·山东滨州·中考真题)如图,在平面直角坐标系中,菱形的一边在轴正半轴上,顶点的坐标为,点是边上的动点,过点作 交边于点,作交边于点,连接.设
的面积为.(1)求关于的函数解析式;(2)当取何值时,的值最大?请求出最大值.
【详解】(1)解:如图所示,过点作于点,连接,∵顶点的坐标为,∴,,
∴,∴,∵四边形是菱形,∴,,,∴是等边三角形,
∴,∵,∴,∴∴是等边三角形,∴∵,∴,∴,∵ ,,则,∴,∴,∴
∴∴
(2)解:∵
∵,∴当时,的值最大,最大值为.
1.(2023·吉林长春·长春市第八十七中学校考三模)如图,反比例函数的图象经过菱形的顶点A,B两点,若轴,菱形的面积为12,点A的纵坐标为1,则k的值为( )
A. B. C.6 D.
【详解】解:作轴于点G,交x轴于点F,
∵四边形是菱形,A,B两点在反比例函数的图象上,且轴,
∴,,
∵点A的纵坐标为1,∴,∴,∴,,
∴,∴,∴,
故选:B.
题型06 菱形与函数的相关问题
正方形的性质:
1)正方形具有平行四边形、矩形、菱形的所有性质.
2)正方形的四个角都是直角,四条边都相等.
3)正方形对边平行且相等.
4)正方形的对角线互相垂直平分且相等,每条对角线平分一组对角;
5)正方形的两条对角线把正方形分成四个全等的等腰直角三角形;
6)正方形既是中心对称图形,也是轴对称图形.
【补充】正方形对角线与边的夹角为45°.
题型07 根据正方形的性质与判定求解
提分笔记
正方形的判定:
1)平行四边形+一组邻边相等+一个角为直角;
2)矩形+一组邻边相等;
3)矩形+对角线互相垂直;
4)菱形+一个角是直角;
5)菱形+对角线相等.
【解题技巧】判定一个四边形是正方形通常先证明它是矩形,再证明它有一组邻边相等或对角线互相垂直;或者先证明它是菱形,再证明它有一个角是直角或对角线相等;还可以先判定四边形是平行四边形,再证明它有一个角为直角和一组邻边相等.
正方形的面积公式: 面积==对角线乘积的一半=2S△ABC=4S△AOB.
正方形的周长公式:周长= 4a
1.(2022·安徽·中考真题)如图,四边形ABCD是正方形,点E在边AD上,△BEF是以E为直角顶点的等腰直角三角形,EF,BF分别交CD于点M,N,过点F作AD的垂线交AD的延长线于点G.连接DF,请完成下列问题:
(1) °;
(2)若,,则 .
【详解】(1)∵四边形ABCD是正方形,∴∠A=90°,AB=AD,∴∠ABE+∠AEB=90°,∵FG⊥AG,∴∠G=∠A=90°,
∵△BEF是等腰直角三角形,∴BE=FE,∠BEF=90°,∴∠AEB+∠FEG=90°,∴∠FEG=∠EBA,
在△ABE和△GEF中,,∴△ABE≌△GEF(AAS),∴AE=FG,AB=GE,
在正方形ABCD中,AB=AD∵AD=AE+DE,EG=DE+DG,∴AE=DG=FG,∴∠FDG=∠DFG=45°.
题型07 根据正方形的性质与判定求解
(2)如图作FH⊥CD于H,∴∠FHD=90°,又∵∠G=∠GDH=90°,∴四边形DGFH是矩形,又∵DG=FG,∴四边形DGFH是正方形,∴DH=FH=DG=2,∴∴,∴DM=,MH=,作MP⊥DF于P,∵∠MDP=∠DMP=45°,∴DP=MP,
∵DP2+MP2=DM2,∴DP=MP=,∴PF=∵∠MFP+∠MFH=∠MFH+∠NFH=45°,∴∠MFP=∠NFH,
∵∠MPF=∠NHF=90°,∴△MPF∽△NHF,∴,即,∴NH=,∴MN=MH+NH=+=.故填: .
1.(2023·吉林长春·二模)如图①,在正方形中,,M为对角线上一点(不与B、D重合),连接,过点M作交边于点N,连接.
(1)【问题发现】在图①中小明想过点M分别作的垂线,发现和有特殊的关系,请你判断的形状,并根据小明的方法给出证明;
(2)【问题解决】直接写出图①中的取值范围: ;
(3)【类比探究】如图②,在矩形中,,M为对角线上一点,
且,则 .
题型07 根据正方形的性质与判定求解
【分析】(1)如图:过点M作于E,于F,则四边形为矩形,
再说明四边形为正方形可得,进而证得可得即可解答;
(2)由是等腰直角三角形可知当时,有最小值,进而求得最小值;再根据题意可知,则即可解答;
(3)如图:过点M作于G,延长交于H,则,先证明可得,进而解得,再证可得,进而求得、,最后根据三角形的面公式即可解答
1.(2020·内蒙古鄂尔多斯·中考真题)如图,已知正方形ABCD,点M是边BA延长线上的动点(不与点A重合),且AM<AB,△CBE由平移得到,若过点E作EH⊥AC,H为垂足,则有以下结论:
①点M位置变化,使得∠DHC=60°时,2BE=DM;②无论点M运动到何处,都有DM=HM;
③在点M的运动过程中,四边形CEMD不可能成为菱形;④无论点M运动到何处,∠CHM一定大于135°.
以上结论正确的有 (把所有正确结论的序号都填上).
【详解】解:如图,连接DH,HM.由题可得,AM=BE,∴AB=EM=AD,
∵四边形ABCD是正方形,EH⊥AC,∴EM=AD,∠AHE=90°,∠MEH=∠DAH=45°=∠EAH,
∴EH=AH,∴△MEH≌△DAH(SAS),∴∠MHE=∠DHA,MH=DH,
∴∠MHD=∠AHE=90°,△DHM是等腰直角三角形,∴DM=HM,故②正确;
当∠DHC=60°时,∠ADH=60°﹣45°=15°,∴∠ADM=45°﹣15°=30°,∴Rt△ADM中,DM=2AM,
即DM=2BE,故①正确;
∵CD∥EM,EC∥DM,∴四边形CEMD是平行四边形,
∵DM>AD,AD=CD,∴DM>CD,∴四边形CEMD不可能是菱形,故③正确,
∵点M是边BA延长线上的动点(不与点A重合),且AM<AB,∴∠AHM<∠BAC=45°,
∴∠CHM>135°,故④正确;由上可得正确结论的序号为①②③.故答案为:①②③④.
题型08 根据正方形的性质与判定解决多结论问题
1.(2023·湖北孝感·统考二模)如图,正方形的边长为,点为对角线上一动点点不与、重合,过点作交直线于,将线段绕点逆时针旋转得到线段,连接,,,下列结论:;;;的最小值为,其中正确的是 填写所有正确结论的序号
【提示】过作,,可证得,故正确;可证四边形是正方形,得,,可证,进而得到,所以,得,即,可证正确;由可知,,所以,而可求,正确.由“”可证,可得,当点,点,点三点共线时,有最小值,由勾股定理可求的长,故正确,即可求解.
题型08 根据正方形的性质与判定解决多结论问题
题型09 正方形与函数的相关问题
1.(2023·吉林长春·吉林省第二实验学校校考二模)如图,已知正方形的面积为4,它的两个顶点B,D是反比例函数的图象上两点.若点D的坐标是,则的值为( )
A.3 B. C.2 D.
【详解】解:如图,延长、交y轴于点E、F,延长、交x轴于点M、N,
由的几何意义得,, ∴,
∵, ∴,
∵点D的坐标是, ∴,, ∴,
∵正方形的面积为4, ∴, 而,∴. 故选:D.
题型09 正方形与函数的相关问题
1.(2021·上海·中考真题)定义:在平面内,一个点到图形的距离是这个点到这个图上所有点的最短距离,在平面内有一个正方形,边长为2,中心为O,在正方形外有一点,当正方形绕着点O旋转时,则点P到正方形的最短距离d的取值范围为 .
【详解】解:如图1,设的中点为E,连接OA,OE,则AE=OE=1,∠AEO=90°,.
∴点O与正方形边上的所有点的连线中,
最小,等于1,最大,等于.
∵,∴点P与正方形边上的所有点的连线中,
如图2所示,当点E落在上时,最大值PE=PO-EO=2-1=1;
如图3所示,当点A落在上时,最小值.
∴当正方形ABCD绕中心O旋转时,点P到正方形的距离d的取值范围是.
故答案为:
题型10 与特殊四边形有关的新定义问题
1.(2023·广西崇左·二模)筝形的定义:两组邻边分别相等的四边形叫做筝形.
(1)根据筝形的定义,写出一种学过的满足筝形的定义的四边形:______;
(2)如图1,在正方形中,E是对角线延长线上一点,连接.求证:四边形是筝形:
(3)小明学习筝形后对筝形非常感兴趣,购买了一只风筝,通过测量它的主体(如图2)得,,发现它是一个筝形,还得到,,,求筝形的面积.
【提示】(1)根据筝形的定义结合所学知识可得答案;
(2)根据正方形的性质利用证明,得到,再由,即可证明四边形是筝形:
(3)如图所示,过点A作交延长线于E,连接,先证明,推出,求出,得到,进而求出,利用三角形面积公式求出,则.
题型10 与特殊四边形有关的新定义问题
2.(2023·广东广州·一模)定义新概念:有一组邻边相等,且它们的夹角是直角的凸四边形叫做等腰直角四边形.
(1)如图①,等腰直角四边形,,.
①若,于点,求的长;
②若,,求的长;
(2)如图②,在矩形中,,点是对角线上的一点,且,过点作直线分别交边,于点,,要使四边形是等腰直角四边形,求的长.
【提示】(1)①根据勾股定理求出,再根据勾股定理求出的值;
②连接、,交于点,过点C作,交于点E,证明垂直平分,得出,证明,得出,证明,得出,根据勾股定理求出,即可得出答案;
(2)若,则,,推出四边形表示等腰直角四边形,不符合条件.若与不垂直,当时,此时四边形是等腰直角四边形,当时,此时四边形是等腰直角四边形,分别求解即可.
题型10 与特殊四边形有关的新定义问题
1.(2022·山东烟台·中考真题)如图,正方形ABCD边长为1,以AC为边作第2个正方形ACEF,再以CF为边作第3个正方形FCGH,…,按照这样的规律作下去,第6个正方形的边长为( )A.(2)5 B.(2)6 C.()5 D.()6
【详解】解:由题知,第1个正方形的边长,
根据勾股定理得,第2个正方形的边长,第3个正方形的边长,第4个正方形的边长,第5个正方形的边长,第6个正方形的边长.故选:C.
题型11 与特殊四边形有关的规律探究问题
2.(2023·山东东营·中考真题)如图,在平面直角坐标系中,直线l:与x轴交于点,
以为边作正方形点在y轴上,延长交直线l于点,以为边作正方形,点在y轴上,
以同样的方式依次作正方形,…,正方形,则点的横坐标是 .
【详解】解:当,,解得,∴点,∵是正方形,∴,
∴点,∴点的横坐标是,当时,,解得,∴点,
∵是正方形,∴,∴点,即点的横坐标是,
当时,,解得,∴点,
∵是正方形,∴,∴点的横坐标是,……以此类推,则点的横坐标是故答案为:
1.(2022·广东广州·二模)如图,将4个边长都为2的正方形按如图所示摆放,、、、分别是正方形的中心,若按此规律摆放n个这样的正方形,则这n个正方形两两重叠(阴影)部分的面积之和是 .
【详解】解:由题意可得一个阴影部分面积等于正方形面积的,即是,
5个这样的正方形重叠部分(阴影部分)的面积和为:,
n个这样的正方形重叠部分(阴影部分)的面积和为:.故答案为:.
题型11 与特殊四边形有关的规律探究问题
2.(2022·河北唐山·二模)如图,平面直角坐标系中,边长为1的正方形的顶点A、B分别在x轴、y轴上,点在反比例函数的图象上,过的中点作矩形,使顶点落在反比例函数的图象上,再过的中点作矩形,使顶点落在反比例函数的图象上,…,依此规律可得:
(1)点的坐标为
(2)作出矩形时,落在反比例函数图象上的顶点的坐标为 .
【详解】解:(1)∵正方形OAP1B的边长为1,点P1在反比例函数(x>0)的图象上,
∴P1(1,1),∴k=1, ∴反比例函数的解析式为:,
∵B1是P1A的中点, ∴P2A1=AB1=, ∴OA1=2,∴.
(2)由(1)的解同理,得…∴,当时,.
等腰梯形性质:1)等腰梯形的两底平行,两腰相等;
2)等腰梯形的同一底边上的两个角相等;
3)等腰梯形的两条对角线相等;
4)等腰梯形是轴对称图形(底边的中垂线就是它的对称轴).
等腰梯形判定:1)两腰相等的梯形是等腰梯形;
2)同一底边上的两个角相等的梯形是等腰梯形;
3)对角线相等的梯形是等腰梯形.
【解题思路】判定一个四边形是等腰梯形,必须先判定四边形是梯形,
再证明同一底边上的两个角相等或两腰相等或两条对角线相等.
梯形的面积公式:S=×(上底+下底)×高
题型12 梯形的相关计算
提分笔记
解决梯形问题的常用方法(如下图所示):
1)“作高”:使两腰在两个直角三角形中;
2)“平移对角线”:使两条对角线在同一个三角形中.
3)“延长两腰”:构造具有公共角的两个三角形.
4)“等积变形”:连接梯形上底一端点和另一腰中点,
并延长交下底的延长线于一点,构成三角形.并且这个三角形面积与原来的梯形面积相等.
5)平移腰.过上底端点作一腰的平行线,构造一个平行四边形和三角形.
6)过上底中点平移两腰.构造两个平行四边形和一个三角形.
1.(2023·上海·中考真题)已知在梯形中,连接,且,设.下列两个说法:
①;②则下列说法正确的是( )
A.①正确②错误 B.①错误②正确 C.①②均正确 D.①②均错误
【详解】解:过作,交延长线于,如图所示:
若梯形为等腰梯形,即,时,四边形是平行四边形,
,,, ,即,
又 , ,在中,,,则,
,此时①正确;过作于,如图所示:
在中,,,,则,, ,此时②正确;
而题中,梯形是否为等腰梯形,并未确定;梯形是还是,并未确定,
无法保证①②正确,故选:D.
题型12 梯形的相关计算
1.(2023·上海虹口·二模)如图,在梯形中,,,点E为延长线上一点,,点F在上,联结.
(1)求证:;
(2)如果,求证:四边形为梯形.
【详解】(1)证明:,四边形是等腰梯形
又
,即又
(2),即
,即,
又
四边形为梯形.
题型12 梯形的相关计算
1)垂美四边形
【模型介绍】对角线互相垂直的四边形为垂美四边形.
【性质】四边形中AC⊥BD,则①S垂美四边形ABCD=AC BD ②AB2+DC2=AD2+BC2
2)中点四边形
【模型介绍】依次连接任意一个四边形各边中点所得的四边形叫做中点四边形.
中点四边形的性质:
已知点E、F、G、H分别为四边形ABCD四条边AB、BC、CD、AD的中点,则
①四边形EFGH是平行四边形 ②CEFGH =AC+BD ③sEFGH =sABCD
④顺次连接对角线互相垂直的四边形各边中点所组成的四边形是矩形.
⑤顺次连接对角线相等的四边形各边中点所组成的四边形是菱形.
⑥顺次连接对角线互相垂直且相等的四边形各边中点所组成的四边形是正方形.
速记口诀:矩中菱,菱中矩,正中正.
题型13 四边形的常见几何模型
高分秘籍
3)十字架模型
【模型介绍】如图,在正方形ABCD中,若EF⊥MN,则EF=MN
【易错点】正方形内十字架模型,垂直一定相等,相等不一定垂直.
【解题技巧】无论怎么变,只要垂直,十字架就相等.
4)对角线互补模型
类型一 90°对角互补模型
如图,在四边形ABCD中,若∠ABC=∠ADC=90°,BD平分∠ABC,则
①AD = CD ②AB+BC=BD ③S△ABD+S△BDC=BD2
类型一 120°对角互补模型
如图,已知∠AOB=2∠DCE=120°,OC 平分∠AOB,则
①CD=CE ②OD+OE=OC ③S△DCO+S△COE=
高分秘籍
题型13 四边形的常见几何模型
5)正方形半角模型
【模型介绍】从正方形的一个顶点引出夹角为45°的两条射线,并连结它们与该顶点的两对边的交点构成的基本平面几何模型.
已知正方形ABCD中,E,F分别是BC、CD上的点,∠EAF=45°,AE、AF分别与BD相交于点O、P,则:
①EF=BE+DF ②AE平分∠BEF,AF平分∠DFE ③C CEF=2倍正方形边长
④S ABE +S ADF =S AEF ⑤AB=AG=AD(过点A作AG⊥EF,垂足为点G)
⑥OP2=OB2+OD2 ⑦若点E为BC中点,则点F为CD三等分点
⑧ APO∽ AEF∽ DPF∽ BEO∽ DAO∽ BPA ⑨ABEP四点共圆、AOFD四点共圆、OECFP五点共圆
⑩ APE、 AOF为等腰直角三角形 (11) EF=OP
(12) S AEF=2S APO (13)AB2=BP×OD
(14)CE CF=2BE DF (15) EPC为等腰三角形
(16) PX=BX+DP(过点E作EX⊥BD,垂足为点X)
高分秘籍
题型13 四边形的常见几何模型
1.(2023·辽宁丹东·中考真题)如图,在正方形中,,点E,F分别在边,上,与相交于点G,若,则的长为 .
【详解】解:四边形是正方形,,,
,,,
,,,,
又,, ,
,,, , .
题型13 四边形的常见几何模型
题型13 四边形的常见几何模型
1.(2022·江苏无锡·一模)如图,在正方形ABCD中,点O是对角线BD的中点,点P在线段OD上,连接AP并延长交CD于点E,过点P作PF⊥AP交BC于点F,连接AF、EF,AF交BD于G,现有以下结论:①;②;③;④为定值;⑤.以上结论正确的有( )
A.①②③ B.①②③⑤ C.①②④⑤ D.①②③④⑤
【提示】①正确,证明A、B、F、P四点共圆,推出∠PAG=∠PBF=45°,可得结论;
②正确,将△ADE绕点A顺时针旋转90°得到 △ABM,利用全等三角形的性质证明即可;
③正确,连接PC,过点P作PQ⊥CF于 Q,过点P作PM⊥CD于 W ,则四边形PQCW是矩形,证明FQ=QC,由PB=BQ, PD=PW=CQ=FQ,推出 PB-PD= (BQ-FQ)=BF;
④错误,由△AEF△AMF,推出,因为FM 的长度是变化的,所以△AEF的面积不是定值;
⑤正确.利用相似三角形的性质证明即可.
题型13 四边形的常见几何模型
2.问题背景:“对角互补”是经典的四边形模型,解决相应问题,通常会涉及到旋转构造、全等三角形的证明等综合性较高的几何知识.如果问题中有“,”角度出现,一般会和等腰直角三角形、正方形、等边三角形等特殊图形结合起来考察.
(1)【问题解决】如图①,,平分,小明同学从P点分别向,作垂线,,由此得到正方形,与全等的三角形是________;
(2)【问题探究】如图②,若,,平分,,
,求的长;
(3)【拓展延伸】如图③,点P是正方形外一点,,,
对角线,交于点O,连接,且,求正方形的面积.
题型13 四边形的常见几何模型
【提示】(1)根据角平分线的性质及垂直的定义可得,,进而得四边形是正方形,再根据角的等量代换得,利用可证得,进而可求解.
(2)过点P作于M,于N,根据角平分线的性质可得,利用证得,
进而可得,再利用证得,进而可得,设,则,
,在中,利用直角三角形的特征即可求解.
(3)延长到,使,连接,根据正方形的性质可得,,
利用得,进而可得,.设,
利用勾股定理求得,再利用正方形的面积公式即可求解.
感谢观看
THANK YOU
专题05 四边形的性质与判定
2024年中考数学二轮复习讲练测
目录
CONTENTS
01
02
知识建构
03
考点精讲
考情分析
第一部分
考情分析
02
考点要求 命题预测
平行四边形 平行四边形和特殊平行四边形在中考数学中是占比比较大的一块考点,考察内容主要有各个特殊四边形的性质、判定、以及其应用:考察题型上从选择到填空再都解答题都有,题型变化也比较多样;并且考察难度也都是中等和中等偏上,难度较大,综合性比较强.所以需要考生在复习这块内容的时候一定要准确掌握其性质与判定,并且会在不同的结合问题上注意和其他考点的融合.平行四边形与特殊平行四边形的考察热点有:多边形内角和定理、平行四边形的性质与判定定理、平行四边形的综合应用;矩形、菱形、正方形的性质与判定定理;特殊四边形的图形平移、轴对称、旋转等结合问题.
特殊四边形
第二部分
知识建构
稿定PPT
稿定PPT,海量素材持续更新,上千款模板选择总有一款适合你
02
第三部分
考点精讲
题型01 多边形内角和与外角和综合问题
考点一 平行四边形
多边形的有关计算公式有很多,一定要牢记,代错公式容易导致错误:
①n边形内角和=(n-2)×180°(n≥3).
②从n边形的一个顶点可以引出(n-3)条对角线,n个顶点可以引出n(n-3)条对角线,但是每条对角线计算了两次,因此n边形共有 条对角线.
③n边形的边数=(内角和÷180°)+2.
④n边形的外角和是360°.
⑤n边形的外角和加内角和=n×180°.
⑥在n边形内任取一点O,连接O与各个顶点,把n边形分成n个三角形;在n边形的任意一边上任取一点O,连接O点与其不相邻的其它各顶点的线段可以把n边形分成(n-1)个三角形;连接n边形的任一顶点A与其不相邻的各个顶点的线段,把n边形分成(n-2)个三角形.
易错点拨
题型01 多边形内角和与外角和综合问题
1)n边形的内角和随边数的增加而增加,边数每增加1,内角和增加180°.
2)任意多边形的内角和均为180°的整数倍.
3)利用多边形内角和定理可解决三类问题:①已知多边形的边数求内角和;②已知多边形的内角和求边数;③已知足够的角度条件下求某一个内角的度数.
4)任意多边形的外角和等于360°,与多边形的形状和边数无关.
5)正n边形的每个内角为,每一个外角为.
6)正n边形有n条对称轴.
7)对于正n边形,当n为奇数时,是轴对称图形;当n为偶数时,既是轴对称图形,又是中心对称图形.
提分笔记
1.(2023·山东枣庄·中考真题)如图,一束太阳光线平行照射在放置于地面的正六边形上,若,则的度数为( )
A. B. C. D.
【详解】解:如图:∵正六边形的一个外角的度数为:,
∴正六边形的一个内角的度数为:,即:,
∵一束太阳光线平行照射在放置于地面的正六边形上,,∴,
∴,∴;故选B.
2.(2023·新疆·中考真题)一个多边形的每个内角都是,这个多边形是 边形.
【详解】解:∵该多边形每个内角都是,∴该多边形为正多边形,
∴该多边形一个外角,∴该多边形的边数,故答案为:十.
题型01 多边形内角和与外角和综合问题
1.(2023·江西抚州·二模)如图,七边形中,、的延长线交于点O,若、、、的外角和等于,则的度数为( )
A. B. C. D.
【详解】解:五边形的外角和为,且七边形中,
,,,的外角和等于,,
,故选:C.
2.(2023·大同·模拟)等边三角形、正方形及正五边形各一个,按下图放在同一平面内,则( )
A. B. C. D.
【详解】正三角形的每个内角为,
正五边形的每个内角,
正方形的每一个内角为,
∴ ,
故选:A.
题型01 多边形内角和与外角和综合问题
题型02 多边形内角和/外角和的实际应用
1.(2020·山东德州·中考真题)如图,小明从A点出发,沿直线前进8米后向左转45°,再沿直线前进8米,又向左转45°……照这样走下去,他第一次回到出发点A时,共走路程为( )
A.80米 B.96米 C.64米 D.48米
题型02 多边形内角和/外角和的实际应用
2.(2021·江苏镇江·中考真题)如图,花瓣图案中的正六边形ABCDEF的每个内角的度数是 .
【详解】解:设这个正六边形的每一个内角的度数为x,
则6x=(6﹣2) 180°,
解得x=120°.
故答案为:120°.
题型03 利用平行四边形的性质与判定求解
平行四边形的性质:1)对边平行且相等; 2)对角相等、邻角互补; 3)对角线互相平分;
4)平行四边形是中心对称图形,但不是轴对称图形,平行四边形的对角线的交点是平行四边形的对称中心.
【解题技巧】
1)平行四边形相邻两边之和等于周长的一半.
2)平行四边形中有相等的边、角和平行关系,所以经常需结合三角形全等来解题.
3)过平行四边形对称中心的任一直线等分平行四边形的面积及周长.
4)如图①,AE平分∠BAD,则可利用平行线的性质结合等角对等边得到△ABE为等腰三角形,即AB=BE.
5)如图②,已知点E为AD上一点,根据平行线间的距离处处相等,可得S△BEC=S△ABE+S△CDE.
6)如图③,根据平行四边形的面积的求法,可得AE·BC=AF·CD.
解题大招
平行四边形的判定定理:
①定义:两组对边分别平行的四边形是平行四边形.
②一组对边平行且相等的四边形是平行四边形.
③两组对边分别相等的四边形是平行四边形.
④两组对角分别相等的四边形是平行四边形.
⑤对角线互相平分的四边形是平行四边形.
【解题技巧】
一般地,要判定一个四边形是平行四边形有多种方法,主要有以下三种思路:
1)当已知条件中有关于所证四边形的角时,可用“两组对角分别相等的四边形是平行四边形”来证明;
2)当已知条件中有关于所证四边形的边时,可选择“两组对边分别相等的四边形是平行四边形”或“两组对边分别平行的四边形是平行四边形”或“有一组对边平行且相等的四边形是平行四边形”来证明;
3)当已知条件中有关于所证四边形的对角线时,可选择“对角线互相平分的四边形是平行四边形”来证明.
题型03 利用平行四边形的性质与判定求解
解题大招
1.(2023·浙江湖州·中考真题)如图,已知,以点O为圆心,适当长为半径作圆弧,与角的两边分别交于C,D两点,分别以点C,D为圆心,大于长为半径作圆弧,两条圆弧交于内一点P,连接,过点P作直线,交OB于点E,过点P作直线,交于点F.若,,则四边形的面积是( )
A. B. C. D.
【详解】解:过P作于M,由作图得:平分,∴,∴,∴,
∵,,∴四边形为平行四边形,,∴,∴,
设,在中,,即:,解得:,
∴.故选:B.
题型03 利用平行四边形的性质与判定求解
2.(2023·辽宁·中考真题)如图,平行四边形的对角线,相交于点,过点作,交的延长线于点,连接,交于点,则四边形的面积与的面积的比值为 .
【详解】解:∵四边形是平行四边形,∴,,又∵,∴四边形是平行四边形,,∴,
∵,∴,,∴,∴,,∴,,∴同理,∵,∴,
设,则,,
∴∴,故答案为∶
1.(2024·陕西西安·模拟预测)如图, 菱形中, 对角线交于点O,, 垂足为点H,
分别交及的延长线于点E、M、F,且,则的值为( )
A. B. C. D.
【详解】解:∵四边形是菱形,∴,,,∵,∴,∴四边形是平行四边形,∴,∵,∴,∴,∴,
∵∴,∴,∴,故选:D.
题型03 利用平行四边形的性质与判定求解
题型04 利用平行四边形的性质与判定解决多结论问题
1.(2022·山东泰安·中考真题)如图,平行四边形的对角线,相交于点O.点E为的中点,连接并延长交于点F,,.下列结论:①;②;③四边形是菱形;④.
其中正确结论的个数是( )A.4 B.3 C.2 D.1
1.(2023·辽宁抚顺·二模)如图,在平行四边形中,,E,F分别是上的动点,且,连接,与相交于P,过点P作,交于M,交于N,当E,F在上移动时,下列结论:①;②;③;④.其中正确的有 .(填序号)
【详解】解:∵平行四边形中,,∴,,∴,∵,∴,∴,故①正确;∴,故②正确;∵,∴与之间的距离相等,∴,故④正确;
∵,即,∵,∴,,∴,,∴,
∴,故③正确;综上,①②③④都正确,
题型04 利用平行四边形的性质与判定解决多结论问题
题型05 构建三角形中位线解决问题
构造三角形中位线的常用方法:
1)连接两点构造三角形中位线;
2) 已知中点,取另一条线段的中点构造中位线.
3) 利用角平分线+垂直构造三角形的中位线.
高分秘籍
1.(2023·广西·中考真题)如图,在边长为2的正方形中,E,F分别是上的动点,M,N分别是的中点,则的最大值为 .
【详解】如图所示,连接,
∵M,N分别是的中点,∴是的中位线,∴,
∵四边形是正方形,∴,∴,
∴当最大时,最大,此时最大,
∵点E是上的动点,∴当点E和点C重合时,最大,即的长度,
∴此时,∴,∴的最大值为.
2.(2021·天津·中考真题)如图,正方形的边长为4,对角线相交于点O,点E,F分别在的延长线上,且,G为的中点,连接,交于点H,连接,则的长为 .
【详解】解:如图,作OK⊥BC,垂足为点K,
∵正方形边长为4,∴OK=2,KC=2,∴KC=CE,∴CH是△OKE的中位线
∴,作GM⊥CD,垂足为点M,
∵G点为EF中点,∴GM是△FCE的中位线,
∴,,
∴,
在Rt△MHG中,,
故答案为:.
题型05 构建三角形中位线解决问题
1.(2023·山东青岛·模拟预测)如图,四边形顶点是四边形各边中点,若把涂满红油漆需要桶,那么要把其余部分涂满黑颜色,需要 桶
【详解】解:如图所示,连接,∵分别是的中点,∴,
∴∴,同理可得,
则同理可得∴
若把涂满红油漆需要桶,那么要把其余部分涂满黑颜色,需要桶,故答案为:.
题型05 构建三角形中位线解决问题
2.(2023·安徽·二模)如图,在中,,延长到点D,,点E是的中点,交于点F,则的面积为 .
【详解】解:∵,,∴,
∵点E是的中点,∴,取的中点,连接,则:,
∴,∴,∴,
∴,∴;故答案为:.
考点二 特殊四边形
1. 平行四边形、矩形、菱形、正方形之间的关系:
2. 平行四边形、矩形、菱形、正方形的性质
考点二 特殊四边形
3 平行四边形、矩形、菱形、正方形的判定
查漏补缺
题型01 利用矩形的性质与判定求解
矩形的定义:有一个角是直角的平行四边形叫做矩形.
矩形的性质:1)矩形具有平行四边形的所有性质;
2)矩形的四个角都是直角;
3)对角线互相平分且相等;
4)矩形既是中心对称图形,也是轴对称图形.
矩形的对称中心是矩形对角线的交点;
矩形有两条对称轴,矩形的对称轴是过矩形对边中点的直线;
矩形的对称轴过矩形的对称中心.
【推论】1)在直角三角形中斜边的中线,等于斜边的一半.
2)直角三角形中,30度角所对应的直角边等于斜边的一半.
矩形的判定:1) 有一个角是直角的平行四边形是矩形;
2)对角线相等的平行四边形是矩形;
3)有三个角是直角的四边形是矩形.
【解题思路】要证明一个四边形是矩形,首先要判断四边形是否为平行四边形,
若是,则需要再证明对角线相等或有一个角是直角;若不易判断,则可通过证明有三个角是直角来直接证明.
提分笔记
易混易错
1. 对于矩形的定义要注意两点:
a.是平行四边形;
b.有一个角是直角.
2. 定义说有一个角是直角的平行四边形才是矩形,
不要错误地理解为有一个角是直角的四边形是矩形.
1.(2023·四川雅安·中考真题)如图,在中,.P为边上一动点,作于点D,于点E,则的最小值为 .
【详解】解:如图,连接,∵,∴,
∵于点D,于点E,,∴四边形是矩形,
∴,由垂线段最短可得时,线段的值最小,此时线段的值最小,
此时,,代入数据:,∴,∴的最小值为,故答案为:.
题型01 利用矩形的性质与判定求解
2.(2022·内蒙古鄂尔多斯·中考真题)如图,菱形ABCD中,AB=2,∠ABC=60°,矩形BEFG的边EF经过点C,且点G在边AD上,若BG=4,则BE的长为( )A. B. C. D.3
【详解】解:过点G作GM⊥BC于点M,过点C作CN⊥AD于点N,
∵四边形ABCD为菱形,∴AB=BC=CD=,AD=BC,∠ABC=∠D=60°,AD∥BC,
∴∠MGN=90°,∴四边形GMCN为矩形,∴GM=CN,
在△CDN中,∠D=60°,CD=,∴CN=CD sin60°=,∴MG=3,
∵四边形BEFG为矩形,∴∠E=90°,BG∥EF,∴∠BCE=∠GBM,
又∵∠E=∠BMG,∴△GBM∽△BCE,∴,∴,∴BE= ,故选:B.
1.(2024·山西朔州·一模)如图,在矩形中,为对角线上的一点(不与点重合),连接,过点作交边于点,连接.若,则的长为 .
【详解】解:过点作于,延长交于,则,如图:
四边形为矩形,,,,
四边形为矩形,,,,
, ,
, , ,,
, ,
,,,
,,
,, ,即:,解得:,
,
故答案为:.
题型01 利用矩形的性质与判定求解
题型02 与矩形(或正方形)有关的折叠问题
矩形的折叠问题的常用解题思路:
1)对折叠前后的图形进行细致分析,折叠后的图形与原图形全等,对应边、对应角分别相等,找出各相等的边或角;
2)折痕可看作角平分线(对称线段所在的直线与折痕的夹角相等).
3) 折痕可看作垂直平分线(互相重合的两点之间的连线被折痕垂直平分).
4)选择一个直角三角形(不找以折痕为边长的直角三角形),利用未知数表示其它直角三角形三边,通过勾股定理/相似三角形知识求解.
解题大招
1.(2023·黑龙江牡丹江·中考真题)在以“矩形的折叠”为主题的数学活动课上,某位同学进行了如下操作:
第一步:将矩形纸片的一端,利用图①的方法折出一个正方形,然后把纸片展平;
第二步:将图①中的矩形纸片折叠,使点C恰好落在点F处,得到折痕,如图②.
根据以上的操作,若,,则线段的长是( )
A.3 B. C.2 D.1
【详解】解:如图,过点作,交于点,
在和中,
设,则,
,即:,解得:,
,, ,,,
,故选:C.
题型02 与矩形(或正方形)有关的折叠问题
1.(2024·贵州贵阳·模拟预测)如图,在矩形中,,将矩形沿折叠,使点与点重合.
(1)若,求的度数;
(2)求证:;
(3)若,,求的长.
【详解】(1)解:∵四边形是矩形,∴,
由翻折可知: ,∴,∴度数为;
(2)证明:∵四边形是矩形,∴, 由翻折可知: ,,∴,,在和中,,∴;
题型02 与矩形(或正方形)有关的折叠问题
(3)解:设,则,
∵沿翻折后点与点重合,∴,
在中,由勾股定理得,即 ,
解得,∴.
题型03 根据矩形的性质与判定解决多结论问题
1.(2021·山东泰安·中考真题)如图,在平行四边形中,E是的中点,则下列四个结论:①;②若,,则;③若,则;④若,则与全等.其中正确结论的个数为( )A.1个 B.2个 C.3个 D.4个
【详解】解:∵平行四边形中,E是的中点,∴,,,∴,,
∴,∴,∴,故①正确;若,则平行四边形是矩形,由矩形的对角线相等,而点E是矩形的对角线的交点可知,E点到B、C两点的距离相等,∴E点在BC的垂直平分线上,由,可得BN=CN,所以N点是BC的中点,∴MN垂直平分BC,∴,故②正确;若,则BN=2CN,如图1,分别过D、E两点向BC作垂线,垂足分别为Q点和P点,∵E点是BD中点,∴DQ=2EP,∵,∴,故③正确;若,因为,所以,分别过N、C两点向AD作垂线,垂足分别为H、K,由平行线间的距离处处相等可知:NH=CK,∴,∴,∴,∴,又∵,∴,故④正确;故选:D.
(2022·湖南娄底·统考模拟预测)如图,在矩形ABCD中,DE平分交BC于点E,点F是CD边上一点(不与点D重合).点P为DE上一动点,,将绕点P逆时针旋转90°后,角的两边交射线DA于H,G两点,有下列结论:①;②;③;④,其中一定正确的是( )
A.①② B.②③ C.①④ D.③④
【详解】解:根据旋转的性质可知,,
∵DE平分,∴,∴,∴PH=PD,
∵∴
在和中,∵∴∴
∵∴∴故③正确;
∵,∴∴
即,故④正确;
根据已知条件无法证明①DH=DE,②DP=DG.故选:D.
题型03 根据矩形的性质与判定解决多结论问题
题型04 矩形与函数的相关问题
1.(2023·陕西·中考真题)如图,在矩形和正方形中,点A在y轴正半轴上,点C,F均在x轴正半轴上,点D在边上,,.若点B,E在同一个反比例函数的图象上,则这个反比例函数的表达式是 .
【详解】解:∵四边形是矩形,∴,
设正方形的边长为m,∴,
∵,∴,∴,,
设反比例函数的表达式为,∴,
解得或(不合题意,舍去),
∴,∴,∴这个反比例函数的表达式是,
故答案为:.
1.(2022·陕西西安·模拟预测)如图,一次函数的图象交轴于点,交轴于点,点在线段上不与点,重合,过点分别作和的垂线,垂足为,.当矩形的面积为时,点的坐标为( )
A., B. C.,或 D.,或,)
【详解】解:点在线段上不与点,重合,且直线的解析式为,
设点的坐标为,,
,.
矩形的面积为,
,
,,
点的坐标为,或,.
故选:D.
题型04 矩形与函数的相关问题
题型05 根据菱形的性质与判定求解
菱形的性质:
1)具有平行四边形的所有性质;
2)四条边都相等;
3)两条对角线互相垂直,且每条对角线平分一组对角.
4)菱形既是中心对称图形,又是轴对称图形,
菱形的对称中心是菱形对角线的交点,
菱形的对称轴是菱形对角线所在的直线,
菱形的对称轴过菱形的对称中心.
菱形的判定:
1)对角线互相垂直的平行四边形是菱形.
2)一组邻边相等的平行四边形是菱形.
3)四条边相等的四边形是菱形.
【解题思路】判定一个四边形是菱形时,可先说明它是平行四边形,
再说明它的一组邻边相等或它的对角线互相垂直,也可直接说明它的四条边都相等或它的对角线互相垂直平分.
菱形的面积公式:S=ah=对角线乘积的一半(其中a为边长,h为高).
菱形的周长公式:周长l=4a(其中a为边长).
提分笔记
易错点拨
1. 对于菱形的定义要注意两点:
a.是平行四边形;
b.一组邻边相等.
2. 定义说有一组邻边相等的平行四边形才是菱形,不要错误地理解为有一组邻边相等的四边形是菱形.
3. 菱形的面积S=对角线乘积的一半,适用于对角线互相垂直的任意四边形的面积的计算.
4. 在求菱形面积时,要根据图形特点及已知条体灵活选择面积公式来解决问题,
5. 在利用对角线长求菱形的面积时,要特别注意不要漏掉计算公式中的 .
(2022·江苏连云港·统考中考真题)如图,四边形为平行四边形,延长到点,使,且.
(1)求证:四边形为菱形;
(2)若是边长为2的等边三角形,点、、分别在线段、、上运动,求的最小值.
【详解】(1)证明:∵四边形是平行四边形,∴,,
∵,∴,又∵点在的延长线上,
∴,∴四边形为平行四边形,
又∵,∴四边形为菱形.
题型05 根据菱形的性质与判定求解
(2)解:如图,由菱形对称性得,点关于的对称点在上,∴,
当、、共线时,,
过点作,垂足为,
∵,∴的最小值即为平行线间的距离的长,
∵是边长为2的等边三角形,∴在中,,,,
∴,∴的最小值为.
1.(2023·湖南株洲·模拟预测)如图,菱形ABCD的对角线AC与BD相交于点O,E为AD的中点,连接OE,,,则( )
A.4 B. C.2 D.
【详解】是菱形,E为AD的中点,
,.
是直角三角形,.
,,
,.
,即,
,.
故选:C.
题型05 根据菱形的性质与判定求解
题型06 菱形与函数的相关问题
1.(2023·山东滨州·中考真题)如图,在平面直角坐标系中,菱形的一边在轴正半轴上,顶点的坐标为,点是边上的动点,过点作 交边于点,作交边于点,连接.设
的面积为.(1)求关于的函数解析式;(2)当取何值时,的值最大?请求出最大值.
【详解】(1)解:如图所示,过点作于点,连接,∵顶点的坐标为,∴,,
∴,∴,∵四边形是菱形,∴,,,∴是等边三角形,
∴,∵,∴,∴∴是等边三角形,∴∵,∴,∴,∵ ,,则,∴,∴,∴
∴∴
(2)解:∵
∵,∴当时,的值最大,最大值为.
1.(2023·吉林长春·长春市第八十七中学校考三模)如图,反比例函数的图象经过菱形的顶点A,B两点,若轴,菱形的面积为12,点A的纵坐标为1,则k的值为( )
A. B. C.6 D.
【详解】解:作轴于点G,交x轴于点F,
∵四边形是菱形,A,B两点在反比例函数的图象上,且轴,
∴,,
∵点A的纵坐标为1,∴,∴,∴,,
∴,∴,∴,
故选:B.
题型06 菱形与函数的相关问题
正方形的性质:
1)正方形具有平行四边形、矩形、菱形的所有性质.
2)正方形的四个角都是直角,四条边都相等.
3)正方形对边平行且相等.
4)正方形的对角线互相垂直平分且相等,每条对角线平分一组对角;
5)正方形的两条对角线把正方形分成四个全等的等腰直角三角形;
6)正方形既是中心对称图形,也是轴对称图形.
【补充】正方形对角线与边的夹角为45°.
题型07 根据正方形的性质与判定求解
提分笔记
正方形的判定:
1)平行四边形+一组邻边相等+一个角为直角;
2)矩形+一组邻边相等;
3)矩形+对角线互相垂直;
4)菱形+一个角是直角;
5)菱形+对角线相等.
【解题技巧】判定一个四边形是正方形通常先证明它是矩形,再证明它有一组邻边相等或对角线互相垂直;或者先证明它是菱形,再证明它有一个角是直角或对角线相等;还可以先判定四边形是平行四边形,再证明它有一个角为直角和一组邻边相等.
正方形的面积公式: 面积==对角线乘积的一半=2S△ABC=4S△AOB.
正方形的周长公式:周长= 4a
1.(2022·安徽·中考真题)如图,四边形ABCD是正方形,点E在边AD上,△BEF是以E为直角顶点的等腰直角三角形,EF,BF分别交CD于点M,N,过点F作AD的垂线交AD的延长线于点G.连接DF,请完成下列问题:
(1) °;
(2)若,,则 .
【详解】(1)∵四边形ABCD是正方形,∴∠A=90°,AB=AD,∴∠ABE+∠AEB=90°,∵FG⊥AG,∴∠G=∠A=90°,
∵△BEF是等腰直角三角形,∴BE=FE,∠BEF=90°,∴∠AEB+∠FEG=90°,∴∠FEG=∠EBA,
在△ABE和△GEF中,,∴△ABE≌△GEF(AAS),∴AE=FG,AB=GE,
在正方形ABCD中,AB=AD∵AD=AE+DE,EG=DE+DG,∴AE=DG=FG,∴∠FDG=∠DFG=45°.
题型07 根据正方形的性质与判定求解
(2)如图作FH⊥CD于H,∴∠FHD=90°,又∵∠G=∠GDH=90°,∴四边形DGFH是矩形,又∵DG=FG,∴四边形DGFH是正方形,∴DH=FH=DG=2,∴∴,∴DM=,MH=,作MP⊥DF于P,∵∠MDP=∠DMP=45°,∴DP=MP,
∵DP2+MP2=DM2,∴DP=MP=,∴PF=∵∠MFP+∠MFH=∠MFH+∠NFH=45°,∴∠MFP=∠NFH,
∵∠MPF=∠NHF=90°,∴△MPF∽△NHF,∴,即,∴NH=,∴MN=MH+NH=+=.故填: .
1.(2023·吉林长春·二模)如图①,在正方形中,,M为对角线上一点(不与B、D重合),连接,过点M作交边于点N,连接.
(1)【问题发现】在图①中小明想过点M分别作的垂线,发现和有特殊的关系,请你判断的形状,并根据小明的方法给出证明;
(2)【问题解决】直接写出图①中的取值范围: ;
(3)【类比探究】如图②,在矩形中,,M为对角线上一点,
且,则 .
题型07 根据正方形的性质与判定求解
【分析】(1)如图:过点M作于E,于F,则四边形为矩形,
再说明四边形为正方形可得,进而证得可得即可解答;
(2)由是等腰直角三角形可知当时,有最小值,进而求得最小值;再根据题意可知,则即可解答;
(3)如图:过点M作于G,延长交于H,则,先证明可得,进而解得,再证可得,进而求得、,最后根据三角形的面公式即可解答
1.(2020·内蒙古鄂尔多斯·中考真题)如图,已知正方形ABCD,点M是边BA延长线上的动点(不与点A重合),且AM<AB,△CBE由平移得到,若过点E作EH⊥AC,H为垂足,则有以下结论:
①点M位置变化,使得∠DHC=60°时,2BE=DM;②无论点M运动到何处,都有DM=HM;
③在点M的运动过程中,四边形CEMD不可能成为菱形;④无论点M运动到何处,∠CHM一定大于135°.
以上结论正确的有 (把所有正确结论的序号都填上).
【详解】解:如图,连接DH,HM.由题可得,AM=BE,∴AB=EM=AD,
∵四边形ABCD是正方形,EH⊥AC,∴EM=AD,∠AHE=90°,∠MEH=∠DAH=45°=∠EAH,
∴EH=AH,∴△MEH≌△DAH(SAS),∴∠MHE=∠DHA,MH=DH,
∴∠MHD=∠AHE=90°,△DHM是等腰直角三角形,∴DM=HM,故②正确;
当∠DHC=60°时,∠ADH=60°﹣45°=15°,∴∠ADM=45°﹣15°=30°,∴Rt△ADM中,DM=2AM,
即DM=2BE,故①正确;
∵CD∥EM,EC∥DM,∴四边形CEMD是平行四边形,
∵DM>AD,AD=CD,∴DM>CD,∴四边形CEMD不可能是菱形,故③正确,
∵点M是边BA延长线上的动点(不与点A重合),且AM<AB,∴∠AHM<∠BAC=45°,
∴∠CHM>135°,故④正确;由上可得正确结论的序号为①②③.故答案为:①②③④.
题型08 根据正方形的性质与判定解决多结论问题
1.(2023·湖北孝感·统考二模)如图,正方形的边长为,点为对角线上一动点点不与、重合,过点作交直线于,将线段绕点逆时针旋转得到线段,连接,,,下列结论:;;;的最小值为,其中正确的是 填写所有正确结论的序号
【提示】过作,,可证得,故正确;可证四边形是正方形,得,,可证,进而得到,所以,得,即,可证正确;由可知,,所以,而可求,正确.由“”可证,可得,当点,点,点三点共线时,有最小值,由勾股定理可求的长,故正确,即可求解.
题型08 根据正方形的性质与判定解决多结论问题
题型09 正方形与函数的相关问题
1.(2023·吉林长春·吉林省第二实验学校校考二模)如图,已知正方形的面积为4,它的两个顶点B,D是反比例函数的图象上两点.若点D的坐标是,则的值为( )
A.3 B. C.2 D.
【详解】解:如图,延长、交y轴于点E、F,延长、交x轴于点M、N,
由的几何意义得,, ∴,
∵, ∴,
∵点D的坐标是, ∴,, ∴,
∵正方形的面积为4, ∴, 而,∴. 故选:D.
题型09 正方形与函数的相关问题
1.(2021·上海·中考真题)定义:在平面内,一个点到图形的距离是这个点到这个图上所有点的最短距离,在平面内有一个正方形,边长为2,中心为O,在正方形外有一点,当正方形绕着点O旋转时,则点P到正方形的最短距离d的取值范围为 .
【详解】解:如图1,设的中点为E,连接OA,OE,则AE=OE=1,∠AEO=90°,.
∴点O与正方形边上的所有点的连线中,
最小,等于1,最大,等于.
∵,∴点P与正方形边上的所有点的连线中,
如图2所示,当点E落在上时,最大值PE=PO-EO=2-1=1;
如图3所示,当点A落在上时,最小值.
∴当正方形ABCD绕中心O旋转时,点P到正方形的距离d的取值范围是.
故答案为:
题型10 与特殊四边形有关的新定义问题
1.(2023·广西崇左·二模)筝形的定义:两组邻边分别相等的四边形叫做筝形.
(1)根据筝形的定义,写出一种学过的满足筝形的定义的四边形:______;
(2)如图1,在正方形中,E是对角线延长线上一点,连接.求证:四边形是筝形:
(3)小明学习筝形后对筝形非常感兴趣,购买了一只风筝,通过测量它的主体(如图2)得,,发现它是一个筝形,还得到,,,求筝形的面积.
【提示】(1)根据筝形的定义结合所学知识可得答案;
(2)根据正方形的性质利用证明,得到,再由,即可证明四边形是筝形:
(3)如图所示,过点A作交延长线于E,连接,先证明,推出,求出,得到,进而求出,利用三角形面积公式求出,则.
题型10 与特殊四边形有关的新定义问题
2.(2023·广东广州·一模)定义新概念:有一组邻边相等,且它们的夹角是直角的凸四边形叫做等腰直角四边形.
(1)如图①,等腰直角四边形,,.
①若,于点,求的长;
②若,,求的长;
(2)如图②,在矩形中,,点是对角线上的一点,且,过点作直线分别交边,于点,,要使四边形是等腰直角四边形,求的长.
【提示】(1)①根据勾股定理求出,再根据勾股定理求出的值;
②连接、,交于点,过点C作,交于点E,证明垂直平分,得出,证明,得出,证明,得出,根据勾股定理求出,即可得出答案;
(2)若,则,,推出四边形表示等腰直角四边形,不符合条件.若与不垂直,当时,此时四边形是等腰直角四边形,当时,此时四边形是等腰直角四边形,分别求解即可.
题型10 与特殊四边形有关的新定义问题
1.(2022·山东烟台·中考真题)如图,正方形ABCD边长为1,以AC为边作第2个正方形ACEF,再以CF为边作第3个正方形FCGH,…,按照这样的规律作下去,第6个正方形的边长为( )A.(2)5 B.(2)6 C.()5 D.()6
【详解】解:由题知,第1个正方形的边长,
根据勾股定理得,第2个正方形的边长,第3个正方形的边长,第4个正方形的边长,第5个正方形的边长,第6个正方形的边长.故选:C.
题型11 与特殊四边形有关的规律探究问题
2.(2023·山东东营·中考真题)如图,在平面直角坐标系中,直线l:与x轴交于点,
以为边作正方形点在y轴上,延长交直线l于点,以为边作正方形,点在y轴上,
以同样的方式依次作正方形,…,正方形,则点的横坐标是 .
【详解】解:当,,解得,∴点,∵是正方形,∴,
∴点,∴点的横坐标是,当时,,解得,∴点,
∵是正方形,∴,∴点,即点的横坐标是,
当时,,解得,∴点,
∵是正方形,∴,∴点的横坐标是,……以此类推,则点的横坐标是故答案为:
1.(2022·广东广州·二模)如图,将4个边长都为2的正方形按如图所示摆放,、、、分别是正方形的中心,若按此规律摆放n个这样的正方形,则这n个正方形两两重叠(阴影)部分的面积之和是 .
【详解】解:由题意可得一个阴影部分面积等于正方形面积的,即是,
5个这样的正方形重叠部分(阴影部分)的面积和为:,
n个这样的正方形重叠部分(阴影部分)的面积和为:.故答案为:.
题型11 与特殊四边形有关的规律探究问题
2.(2022·河北唐山·二模)如图,平面直角坐标系中,边长为1的正方形的顶点A、B分别在x轴、y轴上,点在反比例函数的图象上,过的中点作矩形,使顶点落在反比例函数的图象上,再过的中点作矩形,使顶点落在反比例函数的图象上,…,依此规律可得:
(1)点的坐标为
(2)作出矩形时,落在反比例函数图象上的顶点的坐标为 .
【详解】解:(1)∵正方形OAP1B的边长为1,点P1在反比例函数(x>0)的图象上,
∴P1(1,1),∴k=1, ∴反比例函数的解析式为:,
∵B1是P1A的中点, ∴P2A1=AB1=, ∴OA1=2,∴.
(2)由(1)的解同理,得…∴,当时,.
等腰梯形性质:1)等腰梯形的两底平行,两腰相等;
2)等腰梯形的同一底边上的两个角相等;
3)等腰梯形的两条对角线相等;
4)等腰梯形是轴对称图形(底边的中垂线就是它的对称轴).
等腰梯形判定:1)两腰相等的梯形是等腰梯形;
2)同一底边上的两个角相等的梯形是等腰梯形;
3)对角线相等的梯形是等腰梯形.
【解题思路】判定一个四边形是等腰梯形,必须先判定四边形是梯形,
再证明同一底边上的两个角相等或两腰相等或两条对角线相等.
梯形的面积公式:S=×(上底+下底)×高
题型12 梯形的相关计算
提分笔记
解决梯形问题的常用方法(如下图所示):
1)“作高”:使两腰在两个直角三角形中;
2)“平移对角线”:使两条对角线在同一个三角形中.
3)“延长两腰”:构造具有公共角的两个三角形.
4)“等积变形”:连接梯形上底一端点和另一腰中点,
并延长交下底的延长线于一点,构成三角形.并且这个三角形面积与原来的梯形面积相等.
5)平移腰.过上底端点作一腰的平行线,构造一个平行四边形和三角形.
6)过上底中点平移两腰.构造两个平行四边形和一个三角形.
1.(2023·上海·中考真题)已知在梯形中,连接,且,设.下列两个说法:
①;②则下列说法正确的是( )
A.①正确②错误 B.①错误②正确 C.①②均正确 D.①②均错误
【详解】解:过作,交延长线于,如图所示:
若梯形为等腰梯形,即,时,四边形是平行四边形,
,,, ,即,
又 , ,在中,,,则,
,此时①正确;过作于,如图所示:
在中,,,,则,, ,此时②正确;
而题中,梯形是否为等腰梯形,并未确定;梯形是还是,并未确定,
无法保证①②正确,故选:D.
题型12 梯形的相关计算
1.(2023·上海虹口·二模)如图,在梯形中,,,点E为延长线上一点,,点F在上,联结.
(1)求证:;
(2)如果,求证:四边形为梯形.
【详解】(1)证明:,四边形是等腰梯形
又
,即又
(2),即
,即,
又
四边形为梯形.
题型12 梯形的相关计算
1)垂美四边形
【模型介绍】对角线互相垂直的四边形为垂美四边形.
【性质】四边形中AC⊥BD,则①S垂美四边形ABCD=AC BD ②AB2+DC2=AD2+BC2
2)中点四边形
【模型介绍】依次连接任意一个四边形各边中点所得的四边形叫做中点四边形.
中点四边形的性质:
已知点E、F、G、H分别为四边形ABCD四条边AB、BC、CD、AD的中点,则
①四边形EFGH是平行四边形 ②CEFGH =AC+BD ③sEFGH =sABCD
④顺次连接对角线互相垂直的四边形各边中点所组成的四边形是矩形.
⑤顺次连接对角线相等的四边形各边中点所组成的四边形是菱形.
⑥顺次连接对角线互相垂直且相等的四边形各边中点所组成的四边形是正方形.
速记口诀:矩中菱,菱中矩,正中正.
题型13 四边形的常见几何模型
高分秘籍
3)十字架模型
【模型介绍】如图,在正方形ABCD中,若EF⊥MN,则EF=MN
【易错点】正方形内十字架模型,垂直一定相等,相等不一定垂直.
【解题技巧】无论怎么变,只要垂直,十字架就相等.
4)对角线互补模型
类型一 90°对角互补模型
如图,在四边形ABCD中,若∠ABC=∠ADC=90°,BD平分∠ABC,则
①AD = CD ②AB+BC=BD ③S△ABD+S△BDC=BD2
类型一 120°对角互补模型
如图,已知∠AOB=2∠DCE=120°,OC 平分∠AOB,则
①CD=CE ②OD+OE=OC ③S△DCO+S△COE=
高分秘籍
题型13 四边形的常见几何模型
5)正方形半角模型
【模型介绍】从正方形的一个顶点引出夹角为45°的两条射线,并连结它们与该顶点的两对边的交点构成的基本平面几何模型.
已知正方形ABCD中,E,F分别是BC、CD上的点,∠EAF=45°,AE、AF分别与BD相交于点O、P,则:
①EF=BE+DF ②AE平分∠BEF,AF平分∠DFE ③C CEF=2倍正方形边长
④S ABE +S ADF =S AEF ⑤AB=AG=AD(过点A作AG⊥EF,垂足为点G)
⑥OP2=OB2+OD2 ⑦若点E为BC中点,则点F为CD三等分点
⑧ APO∽ AEF∽ DPF∽ BEO∽ DAO∽ BPA ⑨ABEP四点共圆、AOFD四点共圆、OECFP五点共圆
⑩ APE、 AOF为等腰直角三角形 (11) EF=OP
(12) S AEF=2S APO (13)AB2=BP×OD
(14)CE CF=2BE DF (15) EPC为等腰三角形
(16) PX=BX+DP(过点E作EX⊥BD,垂足为点X)
高分秘籍
题型13 四边形的常见几何模型
1.(2023·辽宁丹东·中考真题)如图,在正方形中,,点E,F分别在边,上,与相交于点G,若,则的长为 .
【详解】解:四边形是正方形,,,
,,,
,,,,
又,, ,
,,, , .
题型13 四边形的常见几何模型
题型13 四边形的常见几何模型
1.(2022·江苏无锡·一模)如图,在正方形ABCD中,点O是对角线BD的中点,点P在线段OD上,连接AP并延长交CD于点E,过点P作PF⊥AP交BC于点F,连接AF、EF,AF交BD于G,现有以下结论:①;②;③;④为定值;⑤.以上结论正确的有( )
A.①②③ B.①②③⑤ C.①②④⑤ D.①②③④⑤
【提示】①正确,证明A、B、F、P四点共圆,推出∠PAG=∠PBF=45°,可得结论;
②正确,将△ADE绕点A顺时针旋转90°得到 △ABM,利用全等三角形的性质证明即可;
③正确,连接PC,过点P作PQ⊥CF于 Q,过点P作PM⊥CD于 W ,则四边形PQCW是矩形,证明FQ=QC,由PB=BQ, PD=PW=CQ=FQ,推出 PB-PD= (BQ-FQ)=BF;
④错误,由△AEF△AMF,推出,因为FM 的长度是变化的,所以△AEF的面积不是定值;
⑤正确.利用相似三角形的性质证明即可.
题型13 四边形的常见几何模型
2.问题背景:“对角互补”是经典的四边形模型,解决相应问题,通常会涉及到旋转构造、全等三角形的证明等综合性较高的几何知识.如果问题中有“,”角度出现,一般会和等腰直角三角形、正方形、等边三角形等特殊图形结合起来考察.
(1)【问题解决】如图①,,平分,小明同学从P点分别向,作垂线,,由此得到正方形,与全等的三角形是________;
(2)【问题探究】如图②,若,,平分,,
,求的长;
(3)【拓展延伸】如图③,点P是正方形外一点,,,
对角线,交于点O,连接,且,求正方形的面积.
题型13 四边形的常见几何模型
【提示】(1)根据角平分线的性质及垂直的定义可得,,进而得四边形是正方形,再根据角的等量代换得,利用可证得,进而可求解.
(2)过点P作于M,于N,根据角平分线的性质可得,利用证得,
进而可得,再利用证得,进而可得,设,则,
,在中,利用直角三角形的特征即可求解.
(3)延长到,使,连接,根据正方形的性质可得,,
利用得,进而可得,.设,
利用勾股定理求得,再利用正方形的面积公式即可求解.
感谢观看
THANK YOU
同课章节目录
