三角形的常见模型课件(共61张PPT) 2023—2024学年苏科版数学八年级上册期末复习
文档属性
| 名称 | 三角形的常见模型课件(共61张PPT) 2023—2024学年苏科版数学八年级上册期末复习 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-03 00:00:00 | ||
图片预览









文档简介
(共61张PPT)
三角形的常见模型
探索新知
随堂训练
目 录
01 探索新知
由3条不在同一直线上的线段,首尾顺次相接组成的图形叫做三角形.
三角形的定义
如图,线段AB、BC、AC是三角形的边.
b
c
a
C
A
B
b
c
a
边也可以用a、b、c来表示。
顶点A所对的边BC用a表示,
顶点B所对的边AC用b表示,
顶点C所对的边AB用c表示。
三角形的边
∠A、∠B、∠C是相邻两边组成的角,叫做三角形的内角,简称三角形的角.
点A、B、C是三角形的顶点.
b
c
a
C
A
B
C
A
B
三角形的内角
三角形的分类
2.三角形按边分类:
三角形
不等边三角形
等腰三角形
等边三角形
底边和腰不等的等腰三角形
1.三角形按角分类:
锐角三角形
直角三角形
钝角三角形
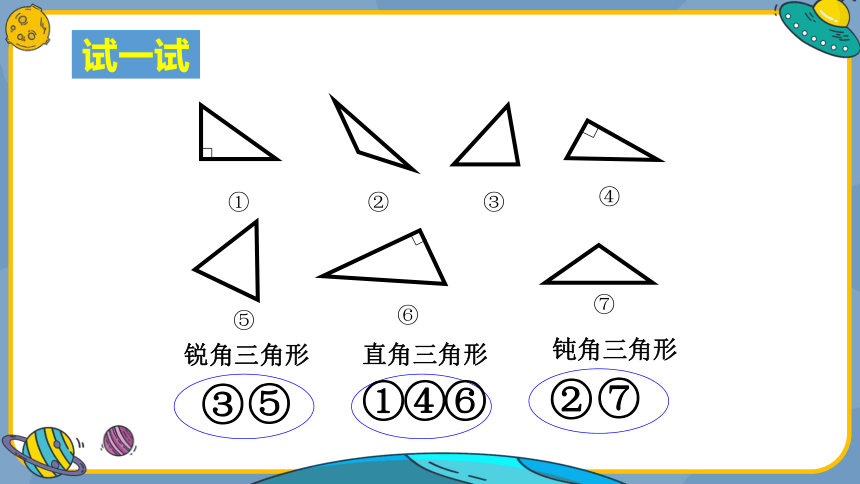
试一试
锐角三角形
直角三角形
钝角三角形
⑦
②
①
③
④
⑤
⑥
①
②
③
④
⑤
⑥
⑦
⑦
②
①
③
④
⑤
⑥
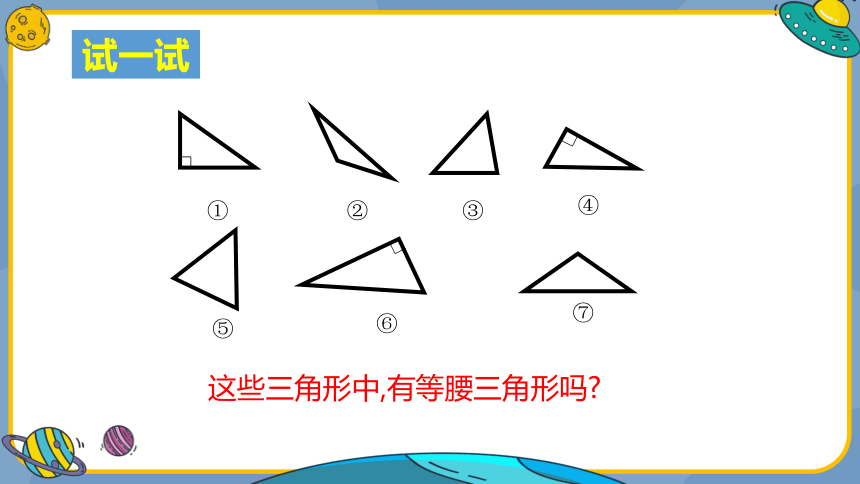
这些三角形中,有等腰三角形吗
试一试
任意两边之和大于第三边。
任意两边之差小于第三边。
A
B
C
a
b
c
你知道为什么吗?
两点之间线段最短!
第三边大于两边之差,小于两边之和.
三角形的三边定理
(1)5cm,8cm,2cm (2)3㎝,3㎝,4㎝
(3)5cm,8cm,13cm (4)3.5㎝,7.5㎝,4.5㎝
例1. 下面分别是三根小木棒的长度,用它们能摆成三角形吗
例题解析
×
√
×
√
3. 已知a、b、c是三角形的三边,且a–1||+(b-2)2=0,那么c的取值范围是多少
练一练
1<c<3
思考题
2.一个等腰三角形的两边分别为4和9,这个三角形的周长是多少
1. 若等腰△ABC周长为26,AB=6,求它的腰长.
10
21
在三角形中,从一个顶点向它的对边所在的直线作垂线,顶点与垂足之间的线段叫做三角形的高线,简称三角形的高.
三角形的高
三角形的角平分线
在三角形中,一个内角的平分线与它的对边相交,这个角的顶点与交点之间的线段叫做三角形的角平分线.
三角形的中线
在三角形中,连接一个顶点与它对边中点的线段,叫做三角形的中线.
例1. 请画出以下各三角形的角平分线,中线,高线。
例题精析
角平分 线交点 中线交点 高线交点
锐角三角形
直角三角形
钝角三角形
在内部
在内部
在内部
在内部
在内部
在内部
在内部
在边上
在外部
归纳总结
如图,∠ACB=90°,AD=BD,DE⊥BC,CF⊥AB,则在△ABC中, 是AB边上的高, 是BC边上的高, 是△ABC的中线 ; 在△BCD中, 是BC边上的高, 是BD边上的高。
F
E
D
C
B
A
练一练
CF
CD
DE
CF
例2. 如图,已知直角三角形ABC中∠ACB=90° CD是AB边上的高,AB=5cm,BC=4cm,AC=3cm, 求(1)△ABC的面积; (2)CD的长
D
A
B
C
练一练
6cm
2.4cm
三角形的八字模型
三角形的八字模型分为角的八字模型和边的八字模型
三角形的角的八字模型
如图所示,AC,BD相交于点O,连接AD、BC,证明:∠A+∠D=∠B+∠C.
三角形角的八字模型
如图所示,AC,BD相交于点O,连接AD、BC,结论:∠A+∠D=∠B+∠C.
证法一:∵∠AOB是△AOD的外角,
∴∠A+∠D=∠AOB
∵∠AOB是△BOC的外角
∴∠B+∠C=∠AOB
∴∠A+∠D=∠B+∠C.
证法二:∵∠A+∠D+∠AOD=180°
∴∠A+∠D=180°-∠AOD
∵∠B+∠C+∠BOC=180°
∴∠B+∠C=180°-∠BOC
又∵∠AOD=∠BOC
∴∠A+∠D=∠B+∠C.
三角形角的八字模型
观察下列图形,计算角度:
(1) 如图①,∠A+∠B+∠C+∠D+∠E=
(2) 如图②,∠A+∠B+∠C+∠D+∠E+∠F=
三角形角的八字模型
解析:解法一:(1)利用角的8字模型,如图③,连接CD,
∵∠BOC是△BOE的外角,
∴∠B+∠E=∠BOC
∵∠BOC是△COD的外角,
∴∠1+∠2=∠BOC
∴∠B+∠E=∠1+∠2(角的8字模型)
∴∠A+∠B+∠ACE+∠ADB+∠E
=∠A+∠ACE+∠ADB+∠1+∠2
=∠A+∠ACD+∠ADC=180°
三角形角的八字模型
解法二:如图④,利用三角形外角和定理,
∵∠1是△FCE的外角
∴∠1=∠C+∠E
∵∠2是△GBD的外角,
∴∠2=∠B+∠D
∴∠A+∠B+∠C+∠D+∠E
=∠A+∠1+∠2=180°
三角形角的八字模型
(1) 解法一:利用角的8字模型,如图⑤
∵∠AOP是△AOB的外角
∴∠A+∠B=∠AOP
∵∠AOP是△OPQ的外角
∴∠1+∠3=∠AOP
∴∠A+∠B=∠1+∠3
同理可得:∠C+∠D=∠1+∠2
∠E+∠F=∠2+∠3.
三角形角的八字模型
解法二:利用角的8字模型
如图⑥,连接DE,
∵∠AOE是△AOB的外角
∴∠A+∠B=∠AOE
∵∠AOE是△OED的外角
∴∠1+∠2=∠AOE
∴∠A+∠B=∠1+∠2(角的8字模型)
∴∠A+∠B+∠C+∠ADC+∠FEB+∠F=360°
三角形边的八字模型
如图所示,AC,BD相交于点O
连接AD,BC。证明:AC+BD>AD+BC
三角形边的八字模型
如图所示,AC,BD相交于点O
连接AD,BC。证明:AC+BD>AD+BC
三角形边的八字模型
模型分析:
∵OA+OD>AD
OB+OC>BC
以上两式进行相加即可得到
OA+OD+OB+OC>BC+AD
即AC+BD>AD+BC
三角形边的八字模型
如图,四边形ABCD的对角线AC,BD相交于点O
求证:(1)AB+BC+CD+AD>AC+BD
(2)AB+BC+CD+AD<2AC+2BD.
三角形边的八字模型
解析:(1)∵AB+BC>AC
CD+AD>AC
AB+AD>BD
BC+CD>BD
以上式子相加即可得到AB+BC+CD+AD>AC+BD
(2)∵AD<OA+OD
BC<OB+OC
两式相加即可得到AD+BC<OA+OD+OB+OC
∴AD+BC<AC+BD(边的8字模型)
同理可证:AB+CD<AC+BD
∴AB+BC+CD+AD<2AC+2BD
三角形的飞镖模型
如图所示,证明∠D=∠A+∠B+∠C
三角形角的飞镖模型
三角形的飞镖模型分为角的飞镖模型和边的飞镖模型
三角形角的飞镖模型
解法一,如图①,作射线AD
∵∠3是△ABD的外角
∴∠3=∠B+∠1
∵∠4是△ACD的外角
∴∠4=∠C+∠2
∴∠BDC=∠3+∠4
∴∠BDC=∠B+∠1+∠2+∠C∴∠BDC=∠BAC+∠B+∠C
三角形角的飞镖模型
解法二:如图②,连接BC
∵∠2+∠4+∠D=180°
∴∠D=180°-(∠2+∠4)
∵∠1+∠2+∠3+∠4+∠A=180°
∴∠A+∠1+∠3=180°-(∠2+∠4)
∴∠D=∠A+∠1+∠3
三角形角的飞镖模型
如图,在四边形ABCD中,AM,CM分别平分∠DAB和∠DCB,AM与CM交于M,探究∠AMC与∠B∠D之间的数量关系.
三角形角的飞镖模型
利用角的飞镖模型
如图所示,连接DM并延长,
∵∠3是△AMD的外角,
∴∠3=∠1+∠ADM
∵∠4是△CMD的外角
∴∠4=∠2+∠CDM
∵∠AMC=∠3+∠4
∴∠AMC=∠1+∠ADM+∠CDM+∠2
∴∠AMC=∠1+∠2+∠ADC(角的飞镖模型)|
利用四边形的内角和,以及AM,CM分别平分∠DAB和∠DCB就可以得出2∠AMC+∠B-∠ADC=360°.
三角形边的飞镖模型
如图所示,证明AB+AC>BD+CD
三角形边的飞镖模型
如图所示,证明AB+AC>BD+CD
三角形边的飞镖模型
解析:如图,延长BD交AC于点E
∵AB+AC=AB+AE+EC
AB+AE>BE
∴AB+AC>BE+EC
∵BE+EC=BD+DE+EC
DE+EC>CD
∴BE+EC>BD+CD
综上:AB+AC>BD+CD
02 随堂训练
3、如图,AD是△ABC的角平分线,DE∥CA,并且交AB于E,DF∥BA,交AC于F,∠1与∠2是否相等 为什么
2
A
B
C
D
E
F
1
练一练
相等
练一练
4、如图,在△ABC中,BC边上的高为( )
A.AD B.BE C.BF D.CG
A
练一练
5、已知小敏家距学校5km,小飞家距小敏家3km.若小飞家距学校距离为xkm,则x满足( )
A.x=2 B.2≤x≤8
C.2≤x≤5 D.2<x<8
B
练一练
6、如图,△ABC的角平分线AD、中线BE相交于点O,则①AO是△ABE的角平分线;②BO是△ABD的中线;③DE是△ADC的中线;④ED是△EBC的角平分线的结论中正确的有( )
A.1个 B.2个 C.3个 D.4个
B
练一练
如图1,求:∠CAD+∠B+∠C+∠D+∠E=
如图2,求:∠CAD+∠B+∠AC+∠D+∠E=
练一练
解析:
如图,连接DE
∠C+∠CAD=∠1+∠2
∠CAD+∠B+∠C+∠ADB+∠BEC=∠B+∠BEC+∠BDA+∠1+∠2=180°
如图,连接DE
∠ACE+∠CAD=∠1+∠2
∠CAD+∠B+∠ACE+∠ADB+∠BEC=∠B+∠BEC+∠BDA+∠1+∠2=180°
练一练
1、如图,求:∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H=
练一练
解析:如图,连接GH,CD
∠E+∠B=∠1+∠2
∠A+∠F=∠3+∠4
∠A+∠B+∠FCH+∠ADG+∠E+∠F+∠DGB+∠EHC
=∠1+∠2+∠3+∠4+∠GDA+∠FCH+∠DGB+∠EHC=360°
练一练
如图,求∠A+∠B+∠C+∠D+∠E+∠F=
练一练
解析:
∠C+∠E+∠D=∠EOC=115°
∠A+∠B+∠F=∠BOF=115°
∠A+∠B+∠C+∠D+∠E+∠F=115°+115°=230°
练一练
如图,求∠A+∠B+∠C+∠D=
练一练
解析:如图所示,连接BD
∠AED=∠A+∠3+∠1
∠BFC=∠2+∠4+∠C
∠A+∠ABF+∠C+∠CDE
=∠A+∠3+∠1+∠2+∠4+∠C=∠AED+∠BFC=220°
练一练
如图,点O为△ABC内部一点
求证:(1)2(AO+BO+CO)>AB+BC+AC;
(2)AB+BC+AC>AO+BO+CO
练一练
如图,点O为△ABC内部一点
求证:(1)2(AO+BO+CO)>AB+BC+AC;
(2)AB+BC+AC>AO+BO+CO
练一练
解析:(1)∵OA+OB>AB ①
OB+OC>BC ②
OC+OA>AC ③
由①+②+③可得
2(AO+BO+CO)>AB+BC+AC;
(2)如图,延长BO交AC于点E
∵AB+AC=AB+AE+EC
AB+AE>BE
∴AB+AC>BE+EC ①
∵BE+EC=BO+OE+EC
OE+EC>CO
∴BE+EC>BO+CO ②
由①②可得AB+AC>BO+CO ③(边的飞镖模型)
同理可得AB+BCD>OA+OC④
BC+AC>OA+OB⑤
由③+④+⑤得AB+BC+AC>AO+BO+CO
练一练
如图,在△ABC中,D、E在BC边上,且BD=CE,求证:AB+AC>AD+AE
练一练
解析:如图,将AC平移至BF,AD延长线于BF相交于点G,连接DF
由平移可得AC=BF
∵AC∥BF
∴∠ACE=∠FBD
∵BD=CE
∴△AEC≌△FDB
∴DF=AE
如图,延长AD交BF于点G
∵AB+BF=AB+BG+GF
∵AB+BG>AG
∴AB+BF>AG+GF ①
∵AG+GF=AD+DG+GF
∵DG+GF>DF
∴AG+GF>AD+DF ②
由①②可得
AB+AC=AB+BF>AD+DF=AD+AE
∴AB+AC>AD+AE.
同学们下课啦!
下次再见!
三角形的常见模型
探索新知
随堂训练
目 录
01 探索新知
由3条不在同一直线上的线段,首尾顺次相接组成的图形叫做三角形.
三角形的定义
如图,线段AB、BC、AC是三角形的边.
b
c
a
C
A
B
b
c
a
边也可以用a、b、c来表示。
顶点A所对的边BC用a表示,
顶点B所对的边AC用b表示,
顶点C所对的边AB用c表示。
三角形的边
∠A、∠B、∠C是相邻两边组成的角,叫做三角形的内角,简称三角形的角.
点A、B、C是三角形的顶点.
b
c
a
C
A
B
C
A
B
三角形的内角
三角形的分类
2.三角形按边分类:
三角形
不等边三角形
等腰三角形
等边三角形
底边和腰不等的等腰三角形
1.三角形按角分类:
锐角三角形
直角三角形
钝角三角形
试一试
锐角三角形
直角三角形
钝角三角形
⑦
②
①
③
④
⑤
⑥
①
②
③
④
⑤
⑥
⑦
⑦
②
①
③
④
⑤
⑥
这些三角形中,有等腰三角形吗
试一试
任意两边之和大于第三边。
任意两边之差小于第三边。
A
B
C
a
b
c
你知道为什么吗?
两点之间线段最短!
第三边大于两边之差,小于两边之和.
三角形的三边定理
(1)5cm,8cm,2cm (2)3㎝,3㎝,4㎝
(3)5cm,8cm,13cm (4)3.5㎝,7.5㎝,4.5㎝
例1. 下面分别是三根小木棒的长度,用它们能摆成三角形吗
例题解析
×
√
×
√
3. 已知a、b、c是三角形的三边,且a–1||+(b-2)2=0,那么c的取值范围是多少
练一练
1<c<3
思考题
2.一个等腰三角形的两边分别为4和9,这个三角形的周长是多少
1. 若等腰△ABC周长为26,AB=6,求它的腰长.
10
21
在三角形中,从一个顶点向它的对边所在的直线作垂线,顶点与垂足之间的线段叫做三角形的高线,简称三角形的高.
三角形的高
三角形的角平分线
在三角形中,一个内角的平分线与它的对边相交,这个角的顶点与交点之间的线段叫做三角形的角平分线.
三角形的中线
在三角形中,连接一个顶点与它对边中点的线段,叫做三角形的中线.
例1. 请画出以下各三角形的角平分线,中线,高线。
例题精析
角平分 线交点 中线交点 高线交点
锐角三角形
直角三角形
钝角三角形
在内部
在内部
在内部
在内部
在内部
在内部
在内部
在边上
在外部
归纳总结
如图,∠ACB=90°,AD=BD,DE⊥BC,CF⊥AB,则在△ABC中, 是AB边上的高, 是BC边上的高, 是△ABC的中线 ; 在△BCD中, 是BC边上的高, 是BD边上的高。
F
E
D
C
B
A
练一练
CF
CD
DE
CF
例2. 如图,已知直角三角形ABC中∠ACB=90° CD是AB边上的高,AB=5cm,BC=4cm,AC=3cm, 求(1)△ABC的面积; (2)CD的长
D
A
B
C
练一练
6cm
2.4cm
三角形的八字模型
三角形的八字模型分为角的八字模型和边的八字模型
三角形的角的八字模型
如图所示,AC,BD相交于点O,连接AD、BC,证明:∠A+∠D=∠B+∠C.
三角形角的八字模型
如图所示,AC,BD相交于点O,连接AD、BC,结论:∠A+∠D=∠B+∠C.
证法一:∵∠AOB是△AOD的外角,
∴∠A+∠D=∠AOB
∵∠AOB是△BOC的外角
∴∠B+∠C=∠AOB
∴∠A+∠D=∠B+∠C.
证法二:∵∠A+∠D+∠AOD=180°
∴∠A+∠D=180°-∠AOD
∵∠B+∠C+∠BOC=180°
∴∠B+∠C=180°-∠BOC
又∵∠AOD=∠BOC
∴∠A+∠D=∠B+∠C.
三角形角的八字模型
观察下列图形,计算角度:
(1) 如图①,∠A+∠B+∠C+∠D+∠E=
(2) 如图②,∠A+∠B+∠C+∠D+∠E+∠F=
三角形角的八字模型
解析:解法一:(1)利用角的8字模型,如图③,连接CD,
∵∠BOC是△BOE的外角,
∴∠B+∠E=∠BOC
∵∠BOC是△COD的外角,
∴∠1+∠2=∠BOC
∴∠B+∠E=∠1+∠2(角的8字模型)
∴∠A+∠B+∠ACE+∠ADB+∠E
=∠A+∠ACE+∠ADB+∠1+∠2
=∠A+∠ACD+∠ADC=180°
三角形角的八字模型
解法二:如图④,利用三角形外角和定理,
∵∠1是△FCE的外角
∴∠1=∠C+∠E
∵∠2是△GBD的外角,
∴∠2=∠B+∠D
∴∠A+∠B+∠C+∠D+∠E
=∠A+∠1+∠2=180°
三角形角的八字模型
(1) 解法一:利用角的8字模型,如图⑤
∵∠AOP是△AOB的外角
∴∠A+∠B=∠AOP
∵∠AOP是△OPQ的外角
∴∠1+∠3=∠AOP
∴∠A+∠B=∠1+∠3
同理可得:∠C+∠D=∠1+∠2
∠E+∠F=∠2+∠3.
三角形角的八字模型
解法二:利用角的8字模型
如图⑥,连接DE,
∵∠AOE是△AOB的外角
∴∠A+∠B=∠AOE
∵∠AOE是△OED的外角
∴∠1+∠2=∠AOE
∴∠A+∠B=∠1+∠2(角的8字模型)
∴∠A+∠B+∠C+∠ADC+∠FEB+∠F=360°
三角形边的八字模型
如图所示,AC,BD相交于点O
连接AD,BC。证明:AC+BD>AD+BC
三角形边的八字模型
如图所示,AC,BD相交于点O
连接AD,BC。证明:AC+BD>AD+BC
三角形边的八字模型
模型分析:
∵OA+OD>AD
OB+OC>BC
以上两式进行相加即可得到
OA+OD+OB+OC>BC+AD
即AC+BD>AD+BC
三角形边的八字模型
如图,四边形ABCD的对角线AC,BD相交于点O
求证:(1)AB+BC+CD+AD>AC+BD
(2)AB+BC+CD+AD<2AC+2BD.
三角形边的八字模型
解析:(1)∵AB+BC>AC
CD+AD>AC
AB+AD>BD
BC+CD>BD
以上式子相加即可得到AB+BC+CD+AD>AC+BD
(2)∵AD<OA+OD
BC<OB+OC
两式相加即可得到AD+BC<OA+OD+OB+OC
∴AD+BC<AC+BD(边的8字模型)
同理可证:AB+CD<AC+BD
∴AB+BC+CD+AD<2AC+2BD
三角形的飞镖模型
如图所示,证明∠D=∠A+∠B+∠C
三角形角的飞镖模型
三角形的飞镖模型分为角的飞镖模型和边的飞镖模型
三角形角的飞镖模型
解法一,如图①,作射线AD
∵∠3是△ABD的外角
∴∠3=∠B+∠1
∵∠4是△ACD的外角
∴∠4=∠C+∠2
∴∠BDC=∠3+∠4
∴∠BDC=∠B+∠1+∠2+∠C∴∠BDC=∠BAC+∠B+∠C
三角形角的飞镖模型
解法二:如图②,连接BC
∵∠2+∠4+∠D=180°
∴∠D=180°-(∠2+∠4)
∵∠1+∠2+∠3+∠4+∠A=180°
∴∠A+∠1+∠3=180°-(∠2+∠4)
∴∠D=∠A+∠1+∠3
三角形角的飞镖模型
如图,在四边形ABCD中,AM,CM分别平分∠DAB和∠DCB,AM与CM交于M,探究∠AMC与∠B∠D之间的数量关系.
三角形角的飞镖模型
利用角的飞镖模型
如图所示,连接DM并延长,
∵∠3是△AMD的外角,
∴∠3=∠1+∠ADM
∵∠4是△CMD的外角
∴∠4=∠2+∠CDM
∵∠AMC=∠3+∠4
∴∠AMC=∠1+∠ADM+∠CDM+∠2
∴∠AMC=∠1+∠2+∠ADC(角的飞镖模型)|
利用四边形的内角和,以及AM,CM分别平分∠DAB和∠DCB就可以得出2∠AMC+∠B-∠ADC=360°.
三角形边的飞镖模型
如图所示,证明AB+AC>BD+CD
三角形边的飞镖模型
如图所示,证明AB+AC>BD+CD
三角形边的飞镖模型
解析:如图,延长BD交AC于点E
∵AB+AC=AB+AE+EC
AB+AE>BE
∴AB+AC>BE+EC
∵BE+EC=BD+DE+EC
DE+EC>CD
∴BE+EC>BD+CD
综上:AB+AC>BD+CD
02 随堂训练
3、如图,AD是△ABC的角平分线,DE∥CA,并且交AB于E,DF∥BA,交AC于F,∠1与∠2是否相等 为什么
2
A
B
C
D
E
F
1
练一练
相等
练一练
4、如图,在△ABC中,BC边上的高为( )
A.AD B.BE C.BF D.CG
A
练一练
5、已知小敏家距学校5km,小飞家距小敏家3km.若小飞家距学校距离为xkm,则x满足( )
A.x=2 B.2≤x≤8
C.2≤x≤5 D.2<x<8
B
练一练
6、如图,△ABC的角平分线AD、中线BE相交于点O,则①AO是△ABE的角平分线;②BO是△ABD的中线;③DE是△ADC的中线;④ED是△EBC的角平分线的结论中正确的有( )
A.1个 B.2个 C.3个 D.4个
B
练一练
如图1,求:∠CAD+∠B+∠C+∠D+∠E=
如图2,求:∠CAD+∠B+∠AC+∠D+∠E=
练一练
解析:
如图,连接DE
∠C+∠CAD=∠1+∠2
∠CAD+∠B+∠C+∠ADB+∠BEC=∠B+∠BEC+∠BDA+∠1+∠2=180°
如图,连接DE
∠ACE+∠CAD=∠1+∠2
∠CAD+∠B+∠ACE+∠ADB+∠BEC=∠B+∠BEC+∠BDA+∠1+∠2=180°
练一练
1、如图,求:∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H=
练一练
解析:如图,连接GH,CD
∠E+∠B=∠1+∠2
∠A+∠F=∠3+∠4
∠A+∠B+∠FCH+∠ADG+∠E+∠F+∠DGB+∠EHC
=∠1+∠2+∠3+∠4+∠GDA+∠FCH+∠DGB+∠EHC=360°
练一练
如图,求∠A+∠B+∠C+∠D+∠E+∠F=
练一练
解析:
∠C+∠E+∠D=∠EOC=115°
∠A+∠B+∠F=∠BOF=115°
∠A+∠B+∠C+∠D+∠E+∠F=115°+115°=230°
练一练
如图,求∠A+∠B+∠C+∠D=
练一练
解析:如图所示,连接BD
∠AED=∠A+∠3+∠1
∠BFC=∠2+∠4+∠C
∠A+∠ABF+∠C+∠CDE
=∠A+∠3+∠1+∠2+∠4+∠C=∠AED+∠BFC=220°
练一练
如图,点O为△ABC内部一点
求证:(1)2(AO+BO+CO)>AB+BC+AC;
(2)AB+BC+AC>AO+BO+CO
练一练
如图,点O为△ABC内部一点
求证:(1)2(AO+BO+CO)>AB+BC+AC;
(2)AB+BC+AC>AO+BO+CO
练一练
解析:(1)∵OA+OB>AB ①
OB+OC>BC ②
OC+OA>AC ③
由①+②+③可得
2(AO+BO+CO)>AB+BC+AC;
(2)如图,延长BO交AC于点E
∵AB+AC=AB+AE+EC
AB+AE>BE
∴AB+AC>BE+EC ①
∵BE+EC=BO+OE+EC
OE+EC>CO
∴BE+EC>BO+CO ②
由①②可得AB+AC>BO+CO ③(边的飞镖模型)
同理可得AB+BCD>OA+OC④
BC+AC>OA+OB⑤
由③+④+⑤得AB+BC+AC>AO+BO+CO
练一练
如图,在△ABC中,D、E在BC边上,且BD=CE,求证:AB+AC>AD+AE
练一练
解析:如图,将AC平移至BF,AD延长线于BF相交于点G,连接DF
由平移可得AC=BF
∵AC∥BF
∴∠ACE=∠FBD
∵BD=CE
∴△AEC≌△FDB
∴DF=AE
如图,延长AD交BF于点G
∵AB+BF=AB+BG+GF
∵AB+BG>AG
∴AB+BF>AG+GF ①
∵AG+GF=AD+DG+GF
∵DG+GF>DF
∴AG+GF>AD+DF ②
由①②可得
AB+AC=AB+BF>AD+DF=AD+AE
∴AB+AC>AD+AE.
同学们下课啦!
下次再见!
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
