2023-2024学年青岛版小学数学六年级下册《期中复习卷》第1-5单元(含答案解析)
文档属性
| 名称 | 2023-2024学年青岛版小学数学六年级下册《期中复习卷》第1-5单元(含答案解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 542.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-03 00:00:00 | ||
图片预览




文档简介
期中复习卷(第1-5单元)(试题)2023-2024学年数学六年级下册青岛版
一、选择题
1.在12个羽毛球场地上同时羽毛球比赛,双打的比单打的多18人,进行双打的有( )人。
A.10 B.28 C.38 D.48
2.如下图,平行四边形a边上的高为b,c边上的高为d。根据这些信息,下列式子成立的有( )个。
①a∶c=b∶d ②a∶c=d∶b ③ ④
A.1 B.2 C.3 D.4
3.甲数的与乙数的相等,甲数的与丙数的相等。比较甲、乙、丙三个数的大小,下列结果正确的是哪一个?( )(甲、乙、丙均不为)
A.甲乙丙 B.丙乙甲 C.甲丙乙 D.丙甲乙
4.把一个底面半径是5厘米的圆锥,完全浸没在一个底面直径是20厘米的圆柱形水槽中(如右图),取出圆锥后,水面下降了3厘米,这个圆锥高( )厘米。
A.6 B.12 C.36 D.48
5.年的6月5日是“世界环境日”,胜利小学的“环保小卫士”对全校师生开展了以“垃圾分类,你我同行”为主题的问卷调查,他们将所有调查结果绘制成了统计图。下面说法正确的是( )。
A.对垃圾分类知识“不了解”的人数占总人数的。
B.对垃圾分类知识“非常了解”的人比“了解一些”的人数多。
C.若“不是很清楚”的人数有88人,则参加本次问卷总人数有400人。
D.如果再随机做一份问卷,某同学一定会回答“了解一些”。
二、填空题
6.今有鸡兔同笼,上有一十五首,下有四十八足,笼中鸡有( )只。
7.在一个比例中,两个比的比值是,两个内项分别是5和8,这个比例是( )。
8.小明步行从家出发,经过超市再到学校。如图是他行走的路线图。已知小明家到超市的距离是800米。根据图中提供的信息回答问题。
(1)超市在小明家( )( )方向800米处。
(2)这幅图的比例尺是( )。
(3)超市和学校之间的实际距离是( )米。
9.中百超市一种矿泉水,零售每瓶卖4元,超市为感谢广大客户对该产品的厚爱,特开展“买三赠一”大酬宾活动,超市的做法优惠了( )%。
10.一件羽绒服原价1050元,“换季促销”活动中打七折出售,买这件羽绒服实际需要花( )元钱。一件棉衣比羽绒服的实际售价少,这件棉衣( )元。
11.一个圆锥形的谷堆,它的底面半径是3米、高是2米,如果每立方米的谷重约为0.7吨,这堆谷的体积是( )立方米,谷约重有( )吨。
12.把一根长2米的圆柱截成3段,表面积增加了60平方分米,这个圆柱原来的体积是( )立方分米。
13.如图是阳光小学红领巾广播站每星期播出各类节目的时间统计(如图),观察填空。
(1)《音乐欣赏》的播出时间占总时间的( )。
(2)《校园快讯》每星期播出72分钟,红领巾广播站每星期共播出节目( )分钟。
(3)《音乐欣赏》每星期的播出时间比《诗书中华》少( )分钟。
三、判断题
14.要表示某小学各年级学生人数与全校学生总人数的关系,应选择扇形统计图。( )
15.车轮的直径一定,所行驶的路程与车轮转数成正比例。( )
16.把一个三角形按2∶1的比放大后,周长和面积都扩大到原来的2倍。( )
17.红星服装厂有职工300人,某天有6人请假,该天的出勤率是94%。( )
18.两个圆锥的底面半径比是1∶2,高相等,体积比为1∶2。( )
19.圆锥的体积是与它等底等高的圆柱体积的3倍。( )
四、计算题
20.直接写出得数。
0.1÷0.001÷7= 9÷30%= 4231÷68≈
()×12= 0.53=
21.求未知数x的值。
①4.25∶x=2.5∶4 ②
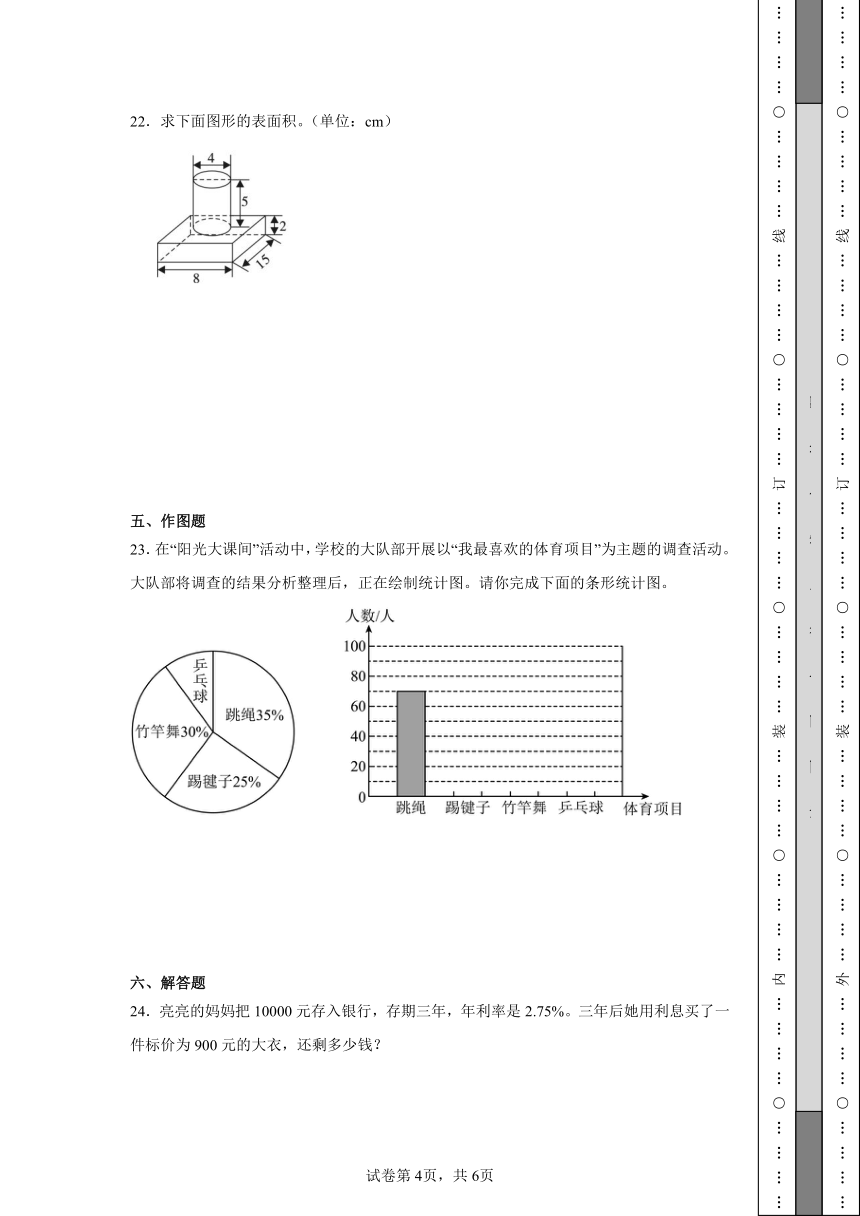
22.求下面图形的表面积。(单位:cm)
五、作图题
23.在“阳光大课间”活动中,学校的大队部开展以“我最喜欢的体育项目”为主题的调查活动。大队部将调查的结果分析整理后,正在绘制统计图。请你完成下面的条形统计图。
六、解答题
24.亮亮的妈妈把10000元存入银行,存期三年,年利率是2.75%。三年后她用利息买了一件标价为900元的大衣,还剩多少钱?
25.某工厂要生产一批电动车,每天生产的辆数和所需的天数如下表。
每天生产的辆数/辆 120 150 160 200 240
所需的天数/天 40 32 30 24 20
(1)每天生产的辆数和所需的天数是不是成反比例关系?说明理由。
(2)如果这批电动车要25天生产完,平均每天要生产多少辆?
26.给一间教室铺地砖,用边长是3分米的地砖共需400块,现在改用边长是4分米的地砖铺,共需多少块地砖?(用比例解)
27.把1.8米长的圆柱形钢材按截成3段,表面积比原来增加了80平方厘米,最短的那段钢材的体积是多少?
28.一个瓶子的下半部分是圆柱形,它的底面积是6平方厘米,瓶高8厘米。在瓶子里面注入高度为4厘米的水(图①),封好瓶口,将其倒立,则水高6厘米(图②)。这个瓶子的容积是多少毫升?
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
) (
学校:___________姓名:___________班级:___________考号:___________
) (
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【分析】单打的2人占一个场地,双打4人占一个场地,双打的比单打的多出的18人,占用(18÷4)个场地,单打的和双打的人数同样多时,单打占用的场地数是双打的2倍,据此先12减去18个双打的占用的场地数,求出单打的和与单打人数相等的双打的共占用多个少场地,再按比例分配求出单打的占用多少个场地,继而求出单打的有多少人,最后用单打人数加上18,即是双打人数。
【详解】(12-18÷4)××2+18
=(12-4.5)××2+18
=7.5××2+18
=5×2+18
=10+18
=28(人)
进行双打的有28人。
故答案为:B
【点睛】解答此题的关键是理解单打的和双打的人数同样多时,单打占用的场地数是双打的2倍,即单打的占用场地数的。
2.C
【分析】根据平行四边形面积公式:面积=底×高;平行四边形面积:ab=cd,再根据比例的基本性质:比例的两个内项之积等于两个外项之积,据此逐项分析,即可解答。
【详解】ab=cd
①a∶c=b∶d;ad=cb,不成立
②a∶c=d∶b;ab=cd,成立;
③=;ab=cd,成立;
④=;ab=cd,成立。
②③④成立。共有3个。
如下图,平行四边形a边上的高为b,c边上的高为d。根据这些信息,下列式子成立的有3个。
故答案为:C
【点睛】熟练掌握平行四边形的面积公式以及比例的基本性质是解答本题的关键。
3.D
【分析】本题可以采用设数法进行分析:将甲数设为20,分别计算出乙与丙表示的数的大小,再进行比较。
设甲数为20,求甲数的用等于4,求甲数的25%用20×25%等于5;
乙数的是4,求乙数用等于16;
丙数的20%是5,求丙数用5÷20%等于25;
【详解】假设甲数是20,
20×25%=5
5÷20%=25
25>20>16,所以丙>甲>乙。
故答案为:D
4.C
【分析】根据题意可知,把圆锥从容器中取出后,下降部分水的就等于圆锥的体积,根据圆柱的体积公式:,先求出下降的水的体积,再利用圆锥的体积公式:,把数据代入公式,求出高即可。
【详解】
=
=
=
=942(厘米)
=
=
=2826÷78.5
=36(厘米)
这个圆锥高36厘米。
故答案为:C
5.C
【分析】A.把总人数看作单位“1”,用1减去“非常了解”、“了解一些”、“不是很清楚”的人数占总人数的百分比,就是“不了解”的人数占总人数的百分比;
B.观察统计图可知,“了解一些”占45%,“非常了解”占28%,比较两个百分比大小,即可解答;
C.把总人数看作单位“1”,“不是很清楚”的人数占总人数的22%,对应的是88人,求单位“1”,用88÷22%解答,再进行比较,即可解答;
D.判断事件发生的可能性有几种情况:可能、不可能、一定,要结合生活实际,做出正确判断。
【详解】A.1-28%-45%-22%
=72%-45%-22%
=37%-22%
=15%
对垃圾分类知识“不了解”的人数占总人数占总调查人数的15%,应小于。原题干说法错误。
B.45%>28%,对垃圾分类知识“非常了解”的人比“了解一些”的人数少。原题干说法错误。
C.88÷22%=400(人)
以若“不是很清楚”的人数有88人,则参加本次问卷总人数有400人。原题干说法正确。
D.如果再随机做一份问卷,某同学不一定会回答“了解一些”。原题干说法错误。
每年的6月5日是“世界环境日”,胜利小学的“环保小卫士”对全校师生开展了以“垃圾分类,你我同行”为主题的问卷调查,他们将所有调查结果绘制成了统计图。下面说法正确的是若“不是很清楚”的人数有88人,则参加本次问卷总人数有400人。
故答案为:C
6.6
【分析】假设全是兔,应有兔足4×15=60只,比实际48只足多了60-48=12只,是因为把每只鸡看作兔子,就多加了2只足,由此可知鸡的只数为12÷2=6只,据此解答。
【详解】(4×15-48)÷(4-2)
=(60-48)÷2
=12÷2
=6(只)
鸡有6只。
7.2∶5=8∶20
【分析】比例的意义:表示两个比相等的式子叫做比例。
两个外项在两个比中,一个外项是比的前项,另一个外项是比的后项;根据“比的前项=比值×后项”,“比的后项=前项÷比值”,据此求出两个外项,再组成比例即可。
【详解】设这个比例式为a∶5=8∶b,那么:
a∶5=,a=×5=2;
8∶b=,b=8÷=8×=20;
所以,这个比例是2∶5=8∶20。(答案不唯一)
8.(1) 南偏东 60
(2)
(3)1200
【分析】(1)根据“上北下南,左西右东”,超市距小明家800米,角度是南偏东60°,据此解答;
(2)比例尺图上距离∶实际距离,据此代入数据解答即可;
(3)根据实际距离图上距离比例尺,代入数据解答即可。
【详解】(1)超市在小明家南偏东60°方向800米处。
(2)2厘米:800米
厘米:80000厘米
即这幅图的比例尺是。
(3)超市和学校的实际距离为:(厘米)=1200(米)
9.25
【分析】已知一种矿泉水每瓶4元,现在“买三赠一”,即现在只需花买3瓶的钱数就可以买到4瓶;
求“买三赠一”优惠了百分之几,就是求现在买4瓶需要的钱数比原来便宜了百分之几;
先根据“总价=单价×数量”,分别求出原来买4瓶需要的钱数与现在买4瓶需要的钱数;然后用减法求出它们的差值,再除以原来买4瓶需要的钱数,即可求解。
【详解】原来买4瓶矿泉水需:4×4=16(元)
现在买4瓶矿泉水需:4×3=12(元)
“买三赠一”优惠了:
(16-12)÷16×100%
=4÷16×100%
=0.25×100%
=25%
超市的做法优惠了25%。
10. 735 441
【分析】打七折即售价是原价的,用原价乘,即可得实际需要花的钱数;把羽绒服的实际售价看作单位“1”,一件棉衣是羽绒服的实际售价的,用乘法计算,即可得这件棉衣的钱数。
【详解】1050×70%
=1050×0.7
=735(元
买这件羽绒服实际需要花735元钱。
(元
这件棉衣441元。
11. 18.84 13.188
【分析】已知圆锥的底面半径和高,根据圆锥的体积公式V=πr2h,代入数据计算即可求出谷堆的体积;再用每立方米谷的重量乘谷堆的体积,即可求出这堆谷的重量。
【详解】×3.14×32×2
=×3.14×9×2
=18.84(立方米)
0.7×18.84=13.188(吨)
这堆谷的体积是18.84立方米,谷约重有13.188吨。
【点睛】本题考查圆锥体积公式的运用。
12.300
【分析】根据锯木问题可知,截的段数比截的次数多1,截成3段需要截2次,每截1次就增加两个截面,那么截2次增加4个截面;已知截成3段后,表面积比原来增加60平方分米,由此可以求出长方体木料的底面积,再根据长方体的体积公式,代入数据计算即可。
【详解】2米分米
(平方分米)
(立方分米)
这根木料的体积是300立方分米。
13.(1)15
(2)180
(3)18
【分析】(1)求《音乐欣赏》的播出时间占总时间的百分数,用1减去《校园快讯》、《国际大事》、《诗书中华》节目的播出时间占总时间的百分数。
(2)求红领巾广播站每星期共播出节目的总时间,用《校园快讯》每星期播出的时间除以《校园快讯》每星期播出的时间占总时间的百分数。
(3)用红领巾广播站每星期共播出节目的总时间分别乘《音乐欣赏》和《诗书中华》节目的播出时间占总时间的百分数,就是《音乐欣赏》和《诗书中华》播出的时间;用《诗书中华》播出的时间减去《音乐欣赏》的播出时间,就是《音乐欣赏》每星期的播出时间比《诗书中华》少的时间。
【详解】(1)
《音乐欣赏》的播出时间占总时间的。
(2)
(分钟)
《校园快讯》每星期播出72分钟,红领巾广播站每星期共播出节目180分钟。
(3)
(分钟)
《音乐欣赏》每星期的播出时间比《诗书中华》少18分钟。
14.√
【分析】条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系。
【详解】某小学各年级学生人数与全校学生总人数的关系是反映部分与整体的关系,应选择扇形统计图。
故答案为:√
15.√
【分析】车轮周长=圆周率×直径,车轮周长=行驶路程÷车轮转数,根据x÷y=k(一定),x和y成正比例关系,据此分析。
【详解】根据圆周率×直径×车轮转数=行驶路程,可得行驶路程÷车轮转数=圆周率×直径,车轮的直径一定,所行驶的路程与车轮转数成正比例,原题说法正确。
故答案为:√
16.×
【分析】根据题意,把一个三角形按2∶1的比放大,那么三角形的三条边都乘2,三角形的底和高也乘2。
根据三角形的周长等于三条边的长度之和,可知三角形的周长扩大到原来的2倍。三角形的面积=底×高÷2,根据积的变化规律可知,三角形的面积扩大到原来的(2×2)倍。
【详解】把一个三角形按2∶1的比放大后,周长扩大到原来的2倍,面积扩大到原来的4倍。
原题说法错误。
故答案为:×
17.×
【分析】根据出勤率=出勤人数÷总人数×100%,代入数据求出出勤率即可判断。
【详解】(300-6)÷300×100%
=294÷300×100%
=0.98×100%
=98%
该天的出勤率是98%,原题说法错误。
故答案为:×
18.×
【分析】两个圆锥的底面半径比是1∶2,将底面半径分别看作1和2,假设高是h,圆锥体积=底面积×高÷3,据此表示出两个圆锥的体积,写出体积比,化简即可。
【详解】(π×12×h÷3)∶(π×22×h÷3)
=12∶22
=1∶4
两个圆锥的底面半径比是1∶2,高相等,体积比为1∶4,所以原题说法错误。
故答案为:×
19.×
【分析】等底等高的圆柱和圆锥,圆锥的体积是圆柱体积的,圆柱的体积是圆锥体积的3倍,据此解答即可。
【详解】根据分析可知,圆锥的体积是与它等底等高的圆柱体积的。
原题干说法错误。
故答案为:×
20.;1;30;60
4;12;0.125;a
【详解】略
21.①x=6.8;②x=42
【分析】①4.25∶x=2.5∶4,解比例,原式化为:2.5x=4.25×4,再根据等式的性质2,方程两边同时除以2.5即可;
②xx=35,先化简方程左边含有x的算式,即求出+的和,再根据等式的性质2,方程的两边同时除以+的和即可。
【详解】①4.25∶x=2.5∶4
解:2.5x=4.25×4
2.5x=17÷2.5
2.5x÷2.5=17÷2.5
x=6.8
②xx=35
解:x+x=35
x=35
x35
x=35×
x=42
22.394.8cm2
【分析】观察图形可知,组合体的表面积=长是8cm,宽是15cm,高是2cm的长方体的表面积+底面半径是4cm的圆柱的侧面积;根据长方体表面积公式:表面积=(长×宽+长×高+宽×高)×2,圆柱的侧面积公式:侧面积=底面周长×高,代入数据,即可解答。
【详解】(8×15+8×2+15×2)×2+3.14×4×5
=(120+16+30)×2+12.56×5
=(136+30)×2+62.8
=166×2+62.8
=332+62.8
=394.8(cm2)
23.见详解
【分析】参加调查的总人数=参加跳绳的人数÷占的百分率;参加其它各项的人数=参加调查的总人数×各自占的百分率,然后依据计算出的人数画出直条,标上数据。
【详解】70÷35%=200(人)
200×25%=50(人)
200×30%=60(人)
200-70-50-60
=130-50-60
=80-60
=20(人)
【点睛】本题考查的是扇形统计图和条形统计图的综合运用,读懂统计图,从统计图中得到必要的信息是解决问题的关键,条形统计图能清楚地表示出每个项目的数据。
24.60元
【分析】根据利息=本金×年利率×存期,据此求出利息;再根据原价×折扣=现价,用利息减去大衣的现价即可求出还剩多少钱。
【详解】
=275×3-765
=825-765
=60(元)
答:还剩60元。
【点睛】本题考查利率问题,明确利息的计算方法是解题的关键。
25.(1)成反比例,见详解;
(2)192辆
【分析】(1)根据表中数据求出每天生产的辆数和所需的天数的乘积,再进一步判断即可。
(2)求平均每天要生产多少辆,用总辆数(120×40)除以时间25天即可。
【详解】(1)每天生产的辆数和所需的天数成反比例关系,理由如下:
因为定值,所以每天生产的辆数和所需的天数成反比例关系。
(2)
(辆)
答:平均每天要生产192辆。
【点睛】此题属于辨识成正、反比例的量以及利用反比例的意义解决实际问题。
26.225块
【分析】由题意可知,教室的总面积不变,则每块地砖的面积和需要地砖的块数成反比例,每块地砖的面积×需要地砖的块数=教室的总面积(一定),据此解答。
【详解】解:设共需x块地砖。
4×4×x=3×3×400
16x=9×400
16x=3600
x=3600÷16
x=225
答:共需225块地砖。
【点睛】本题主要考查反比例的应用,明确题中相关联的两种量成反比例关系是解答题目的关键。
27.600立方厘米
【分析】根据“圆柱形钢材按截成三段”,最短的一段占总长的,用总长乘可以求出最短一段的长度。把钢材截成3段,表面积增加了4个底面的面积,则80平方厘米就是圆柱的4个底面的面积,由此即可求出一个底面的面积。最后根据圆柱的体积=底面积×高,求出最短的一段的体积。
【详解】圆柱底面积:(平方厘米)
最短的一段的高:
=1.8×
=0.3(米
0.3米厘米
(立方厘米)
答:这三段圆钢最短的一段体积是600立方厘米。
28.36毫升
【分析】瓶子的容积=水的体积+空余部分的容积,封好瓶口,将其倒立,空余部分可以转化成高(8-6)厘米的圆柱,根据圆柱体积=底面积×高,分别求出水的体积和空余部分的容积,相加即可。
【详解】6×4+6×(8-6)
=24+6×2
=24+12
=36(立方厘米)
=36(毫升)
答:这个瓶子的容积是36毫升。
答案第1页,共2页
答案第1页,共2页
一、选择题
1.在12个羽毛球场地上同时羽毛球比赛,双打的比单打的多18人,进行双打的有( )人。
A.10 B.28 C.38 D.48
2.如下图,平行四边形a边上的高为b,c边上的高为d。根据这些信息,下列式子成立的有( )个。
①a∶c=b∶d ②a∶c=d∶b ③ ④
A.1 B.2 C.3 D.4
3.甲数的与乙数的相等,甲数的与丙数的相等。比较甲、乙、丙三个数的大小,下列结果正确的是哪一个?( )(甲、乙、丙均不为)
A.甲乙丙 B.丙乙甲 C.甲丙乙 D.丙甲乙
4.把一个底面半径是5厘米的圆锥,完全浸没在一个底面直径是20厘米的圆柱形水槽中(如右图),取出圆锥后,水面下降了3厘米,这个圆锥高( )厘米。
A.6 B.12 C.36 D.48
5.年的6月5日是“世界环境日”,胜利小学的“环保小卫士”对全校师生开展了以“垃圾分类,你我同行”为主题的问卷调查,他们将所有调查结果绘制成了统计图。下面说法正确的是( )。
A.对垃圾分类知识“不了解”的人数占总人数的。
B.对垃圾分类知识“非常了解”的人比“了解一些”的人数多。
C.若“不是很清楚”的人数有88人,则参加本次问卷总人数有400人。
D.如果再随机做一份问卷,某同学一定会回答“了解一些”。
二、填空题
6.今有鸡兔同笼,上有一十五首,下有四十八足,笼中鸡有( )只。
7.在一个比例中,两个比的比值是,两个内项分别是5和8,这个比例是( )。
8.小明步行从家出发,经过超市再到学校。如图是他行走的路线图。已知小明家到超市的距离是800米。根据图中提供的信息回答问题。
(1)超市在小明家( )( )方向800米处。
(2)这幅图的比例尺是( )。
(3)超市和学校之间的实际距离是( )米。
9.中百超市一种矿泉水,零售每瓶卖4元,超市为感谢广大客户对该产品的厚爱,特开展“买三赠一”大酬宾活动,超市的做法优惠了( )%。
10.一件羽绒服原价1050元,“换季促销”活动中打七折出售,买这件羽绒服实际需要花( )元钱。一件棉衣比羽绒服的实际售价少,这件棉衣( )元。
11.一个圆锥形的谷堆,它的底面半径是3米、高是2米,如果每立方米的谷重约为0.7吨,这堆谷的体积是( )立方米,谷约重有( )吨。
12.把一根长2米的圆柱截成3段,表面积增加了60平方分米,这个圆柱原来的体积是( )立方分米。
13.如图是阳光小学红领巾广播站每星期播出各类节目的时间统计(如图),观察填空。
(1)《音乐欣赏》的播出时间占总时间的( )。
(2)《校园快讯》每星期播出72分钟,红领巾广播站每星期共播出节目( )分钟。
(3)《音乐欣赏》每星期的播出时间比《诗书中华》少( )分钟。
三、判断题
14.要表示某小学各年级学生人数与全校学生总人数的关系,应选择扇形统计图。( )
15.车轮的直径一定,所行驶的路程与车轮转数成正比例。( )
16.把一个三角形按2∶1的比放大后,周长和面积都扩大到原来的2倍。( )
17.红星服装厂有职工300人,某天有6人请假,该天的出勤率是94%。( )
18.两个圆锥的底面半径比是1∶2,高相等,体积比为1∶2。( )
19.圆锥的体积是与它等底等高的圆柱体积的3倍。( )
四、计算题
20.直接写出得数。
0.1÷0.001÷7= 9÷30%= 4231÷68≈
()×12= 0.53=
21.求未知数x的值。
①4.25∶x=2.5∶4 ②
22.求下面图形的表面积。(单位:cm)
五、作图题
23.在“阳光大课间”活动中,学校的大队部开展以“我最喜欢的体育项目”为主题的调查活动。大队部将调查的结果分析整理后,正在绘制统计图。请你完成下面的条形统计图。
六、解答题
24.亮亮的妈妈把10000元存入银行,存期三年,年利率是2.75%。三年后她用利息买了一件标价为900元的大衣,还剩多少钱?
25.某工厂要生产一批电动车,每天生产的辆数和所需的天数如下表。
每天生产的辆数/辆 120 150 160 200 240
所需的天数/天 40 32 30 24 20
(1)每天生产的辆数和所需的天数是不是成反比例关系?说明理由。
(2)如果这批电动车要25天生产完,平均每天要生产多少辆?
26.给一间教室铺地砖,用边长是3分米的地砖共需400块,现在改用边长是4分米的地砖铺,共需多少块地砖?(用比例解)
27.把1.8米长的圆柱形钢材按截成3段,表面积比原来增加了80平方厘米,最短的那段钢材的体积是多少?
28.一个瓶子的下半部分是圆柱形,它的底面积是6平方厘米,瓶高8厘米。在瓶子里面注入高度为4厘米的水(图①),封好瓶口,将其倒立,则水高6厘米(图②)。这个瓶子的容积是多少毫升?
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
) (
学校:___________姓名:___________班级:___________考号:___________
) (
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【分析】单打的2人占一个场地,双打4人占一个场地,双打的比单打的多出的18人,占用(18÷4)个场地,单打的和双打的人数同样多时,单打占用的场地数是双打的2倍,据此先12减去18个双打的占用的场地数,求出单打的和与单打人数相等的双打的共占用多个少场地,再按比例分配求出单打的占用多少个场地,继而求出单打的有多少人,最后用单打人数加上18,即是双打人数。
【详解】(12-18÷4)××2+18
=(12-4.5)××2+18
=7.5××2+18
=5×2+18
=10+18
=28(人)
进行双打的有28人。
故答案为:B
【点睛】解答此题的关键是理解单打的和双打的人数同样多时,单打占用的场地数是双打的2倍,即单打的占用场地数的。
2.C
【分析】根据平行四边形面积公式:面积=底×高;平行四边形面积:ab=cd,再根据比例的基本性质:比例的两个内项之积等于两个外项之积,据此逐项分析,即可解答。
【详解】ab=cd
①a∶c=b∶d;ad=cb,不成立
②a∶c=d∶b;ab=cd,成立;
③=;ab=cd,成立;
④=;ab=cd,成立。
②③④成立。共有3个。
如下图,平行四边形a边上的高为b,c边上的高为d。根据这些信息,下列式子成立的有3个。
故答案为:C
【点睛】熟练掌握平行四边形的面积公式以及比例的基本性质是解答本题的关键。
3.D
【分析】本题可以采用设数法进行分析:将甲数设为20,分别计算出乙与丙表示的数的大小,再进行比较。
设甲数为20,求甲数的用等于4,求甲数的25%用20×25%等于5;
乙数的是4,求乙数用等于16;
丙数的20%是5,求丙数用5÷20%等于25;
【详解】假设甲数是20,
20×25%=5
5÷20%=25
25>20>16,所以丙>甲>乙。
故答案为:D
4.C
【分析】根据题意可知,把圆锥从容器中取出后,下降部分水的就等于圆锥的体积,根据圆柱的体积公式:,先求出下降的水的体积,再利用圆锥的体积公式:,把数据代入公式,求出高即可。
【详解】
=
=
=
=942(厘米)
=
=
=2826÷78.5
=36(厘米)
这个圆锥高36厘米。
故答案为:C
5.C
【分析】A.把总人数看作单位“1”,用1减去“非常了解”、“了解一些”、“不是很清楚”的人数占总人数的百分比,就是“不了解”的人数占总人数的百分比;
B.观察统计图可知,“了解一些”占45%,“非常了解”占28%,比较两个百分比大小,即可解答;
C.把总人数看作单位“1”,“不是很清楚”的人数占总人数的22%,对应的是88人,求单位“1”,用88÷22%解答,再进行比较,即可解答;
D.判断事件发生的可能性有几种情况:可能、不可能、一定,要结合生活实际,做出正确判断。
【详解】A.1-28%-45%-22%
=72%-45%-22%
=37%-22%
=15%
对垃圾分类知识“不了解”的人数占总人数占总调查人数的15%,应小于。原题干说法错误。
B.45%>28%,对垃圾分类知识“非常了解”的人比“了解一些”的人数少。原题干说法错误。
C.88÷22%=400(人)
以若“不是很清楚”的人数有88人,则参加本次问卷总人数有400人。原题干说法正确。
D.如果再随机做一份问卷,某同学不一定会回答“了解一些”。原题干说法错误。
每年的6月5日是“世界环境日”,胜利小学的“环保小卫士”对全校师生开展了以“垃圾分类,你我同行”为主题的问卷调查,他们将所有调查结果绘制成了统计图。下面说法正确的是若“不是很清楚”的人数有88人,则参加本次问卷总人数有400人。
故答案为:C
6.6
【分析】假设全是兔,应有兔足4×15=60只,比实际48只足多了60-48=12只,是因为把每只鸡看作兔子,就多加了2只足,由此可知鸡的只数为12÷2=6只,据此解答。
【详解】(4×15-48)÷(4-2)
=(60-48)÷2
=12÷2
=6(只)
鸡有6只。
7.2∶5=8∶20
【分析】比例的意义:表示两个比相等的式子叫做比例。
两个外项在两个比中,一个外项是比的前项,另一个外项是比的后项;根据“比的前项=比值×后项”,“比的后项=前项÷比值”,据此求出两个外项,再组成比例即可。
【详解】设这个比例式为a∶5=8∶b,那么:
a∶5=,a=×5=2;
8∶b=,b=8÷=8×=20;
所以,这个比例是2∶5=8∶20。(答案不唯一)
8.(1) 南偏东 60
(2)
(3)1200
【分析】(1)根据“上北下南,左西右东”,超市距小明家800米,角度是南偏东60°,据此解答;
(2)比例尺图上距离∶实际距离,据此代入数据解答即可;
(3)根据实际距离图上距离比例尺,代入数据解答即可。
【详解】(1)超市在小明家南偏东60°方向800米处。
(2)2厘米:800米
厘米:80000厘米
即这幅图的比例尺是。
(3)超市和学校的实际距离为:(厘米)=1200(米)
9.25
【分析】已知一种矿泉水每瓶4元,现在“买三赠一”,即现在只需花买3瓶的钱数就可以买到4瓶;
求“买三赠一”优惠了百分之几,就是求现在买4瓶需要的钱数比原来便宜了百分之几;
先根据“总价=单价×数量”,分别求出原来买4瓶需要的钱数与现在买4瓶需要的钱数;然后用减法求出它们的差值,再除以原来买4瓶需要的钱数,即可求解。
【详解】原来买4瓶矿泉水需:4×4=16(元)
现在买4瓶矿泉水需:4×3=12(元)
“买三赠一”优惠了:
(16-12)÷16×100%
=4÷16×100%
=0.25×100%
=25%
超市的做法优惠了25%。
10. 735 441
【分析】打七折即售价是原价的,用原价乘,即可得实际需要花的钱数;把羽绒服的实际售价看作单位“1”,一件棉衣是羽绒服的实际售价的,用乘法计算,即可得这件棉衣的钱数。
【详解】1050×70%
=1050×0.7
=735(元
买这件羽绒服实际需要花735元钱。
(元
这件棉衣441元。
11. 18.84 13.188
【分析】已知圆锥的底面半径和高,根据圆锥的体积公式V=πr2h,代入数据计算即可求出谷堆的体积;再用每立方米谷的重量乘谷堆的体积,即可求出这堆谷的重量。
【详解】×3.14×32×2
=×3.14×9×2
=18.84(立方米)
0.7×18.84=13.188(吨)
这堆谷的体积是18.84立方米,谷约重有13.188吨。
【点睛】本题考查圆锥体积公式的运用。
12.300
【分析】根据锯木问题可知,截的段数比截的次数多1,截成3段需要截2次,每截1次就增加两个截面,那么截2次增加4个截面;已知截成3段后,表面积比原来增加60平方分米,由此可以求出长方体木料的底面积,再根据长方体的体积公式,代入数据计算即可。
【详解】2米分米
(平方分米)
(立方分米)
这根木料的体积是300立方分米。
13.(1)15
(2)180
(3)18
【分析】(1)求《音乐欣赏》的播出时间占总时间的百分数,用1减去《校园快讯》、《国际大事》、《诗书中华》节目的播出时间占总时间的百分数。
(2)求红领巾广播站每星期共播出节目的总时间,用《校园快讯》每星期播出的时间除以《校园快讯》每星期播出的时间占总时间的百分数。
(3)用红领巾广播站每星期共播出节目的总时间分别乘《音乐欣赏》和《诗书中华》节目的播出时间占总时间的百分数,就是《音乐欣赏》和《诗书中华》播出的时间;用《诗书中华》播出的时间减去《音乐欣赏》的播出时间,就是《音乐欣赏》每星期的播出时间比《诗书中华》少的时间。
【详解】(1)
《音乐欣赏》的播出时间占总时间的。
(2)
(分钟)
《校园快讯》每星期播出72分钟,红领巾广播站每星期共播出节目180分钟。
(3)
(分钟)
《音乐欣赏》每星期的播出时间比《诗书中华》少18分钟。
14.√
【分析】条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系。
【详解】某小学各年级学生人数与全校学生总人数的关系是反映部分与整体的关系,应选择扇形统计图。
故答案为:√
15.√
【分析】车轮周长=圆周率×直径,车轮周长=行驶路程÷车轮转数,根据x÷y=k(一定),x和y成正比例关系,据此分析。
【详解】根据圆周率×直径×车轮转数=行驶路程,可得行驶路程÷车轮转数=圆周率×直径,车轮的直径一定,所行驶的路程与车轮转数成正比例,原题说法正确。
故答案为:√
16.×
【分析】根据题意,把一个三角形按2∶1的比放大,那么三角形的三条边都乘2,三角形的底和高也乘2。
根据三角形的周长等于三条边的长度之和,可知三角形的周长扩大到原来的2倍。三角形的面积=底×高÷2,根据积的变化规律可知,三角形的面积扩大到原来的(2×2)倍。
【详解】把一个三角形按2∶1的比放大后,周长扩大到原来的2倍,面积扩大到原来的4倍。
原题说法错误。
故答案为:×
17.×
【分析】根据出勤率=出勤人数÷总人数×100%,代入数据求出出勤率即可判断。
【详解】(300-6)÷300×100%
=294÷300×100%
=0.98×100%
=98%
该天的出勤率是98%,原题说法错误。
故答案为:×
18.×
【分析】两个圆锥的底面半径比是1∶2,将底面半径分别看作1和2,假设高是h,圆锥体积=底面积×高÷3,据此表示出两个圆锥的体积,写出体积比,化简即可。
【详解】(π×12×h÷3)∶(π×22×h÷3)
=12∶22
=1∶4
两个圆锥的底面半径比是1∶2,高相等,体积比为1∶4,所以原题说法错误。
故答案为:×
19.×
【分析】等底等高的圆柱和圆锥,圆锥的体积是圆柱体积的,圆柱的体积是圆锥体积的3倍,据此解答即可。
【详解】根据分析可知,圆锥的体积是与它等底等高的圆柱体积的。
原题干说法错误。
故答案为:×
20.;1;30;60
4;12;0.125;a
【详解】略
21.①x=6.8;②x=42
【分析】①4.25∶x=2.5∶4,解比例,原式化为:2.5x=4.25×4,再根据等式的性质2,方程两边同时除以2.5即可;
②xx=35,先化简方程左边含有x的算式,即求出+的和,再根据等式的性质2,方程的两边同时除以+的和即可。
【详解】①4.25∶x=2.5∶4
解:2.5x=4.25×4
2.5x=17÷2.5
2.5x÷2.5=17÷2.5
x=6.8
②xx=35
解:x+x=35
x=35
x35
x=35×
x=42
22.394.8cm2
【分析】观察图形可知,组合体的表面积=长是8cm,宽是15cm,高是2cm的长方体的表面积+底面半径是4cm的圆柱的侧面积;根据长方体表面积公式:表面积=(长×宽+长×高+宽×高)×2,圆柱的侧面积公式:侧面积=底面周长×高,代入数据,即可解答。
【详解】(8×15+8×2+15×2)×2+3.14×4×5
=(120+16+30)×2+12.56×5
=(136+30)×2+62.8
=166×2+62.8
=332+62.8
=394.8(cm2)
23.见详解
【分析】参加调查的总人数=参加跳绳的人数÷占的百分率;参加其它各项的人数=参加调查的总人数×各自占的百分率,然后依据计算出的人数画出直条,标上数据。
【详解】70÷35%=200(人)
200×25%=50(人)
200×30%=60(人)
200-70-50-60
=130-50-60
=80-60
=20(人)
【点睛】本题考查的是扇形统计图和条形统计图的综合运用,读懂统计图,从统计图中得到必要的信息是解决问题的关键,条形统计图能清楚地表示出每个项目的数据。
24.60元
【分析】根据利息=本金×年利率×存期,据此求出利息;再根据原价×折扣=现价,用利息减去大衣的现价即可求出还剩多少钱。
【详解】
=275×3-765
=825-765
=60(元)
答:还剩60元。
【点睛】本题考查利率问题,明确利息的计算方法是解题的关键。
25.(1)成反比例,见详解;
(2)192辆
【分析】(1)根据表中数据求出每天生产的辆数和所需的天数的乘积,再进一步判断即可。
(2)求平均每天要生产多少辆,用总辆数(120×40)除以时间25天即可。
【详解】(1)每天生产的辆数和所需的天数成反比例关系,理由如下:
因为定值,所以每天生产的辆数和所需的天数成反比例关系。
(2)
(辆)
答:平均每天要生产192辆。
【点睛】此题属于辨识成正、反比例的量以及利用反比例的意义解决实际问题。
26.225块
【分析】由题意可知,教室的总面积不变,则每块地砖的面积和需要地砖的块数成反比例,每块地砖的面积×需要地砖的块数=教室的总面积(一定),据此解答。
【详解】解:设共需x块地砖。
4×4×x=3×3×400
16x=9×400
16x=3600
x=3600÷16
x=225
答:共需225块地砖。
【点睛】本题主要考查反比例的应用,明确题中相关联的两种量成反比例关系是解答题目的关键。
27.600立方厘米
【分析】根据“圆柱形钢材按截成三段”,最短的一段占总长的,用总长乘可以求出最短一段的长度。把钢材截成3段,表面积增加了4个底面的面积,则80平方厘米就是圆柱的4个底面的面积,由此即可求出一个底面的面积。最后根据圆柱的体积=底面积×高,求出最短的一段的体积。
【详解】圆柱底面积:(平方厘米)
最短的一段的高:
=1.8×
=0.3(米
0.3米厘米
(立方厘米)
答:这三段圆钢最短的一段体积是600立方厘米。
28.36毫升
【分析】瓶子的容积=水的体积+空余部分的容积,封好瓶口,将其倒立,空余部分可以转化成高(8-6)厘米的圆柱,根据圆柱体积=底面积×高,分别求出水的体积和空余部分的容积,相加即可。
【详解】6×4+6×(8-6)
=24+6×2
=24+12
=36(立方厘米)
=36(毫升)
答:这个瓶子的容积是36毫升。
答案第1页,共2页
答案第1页,共2页
同课章节目录
