2024年中考数学三轮冲刺备考圆专题之模型训练: 圆综合之正A型专项训练(八)(含答案)
文档属性
| 名称 | 2024年中考数学三轮冲刺备考圆专题之模型训练: 圆综合之正A型专项训练(八)(含答案) | 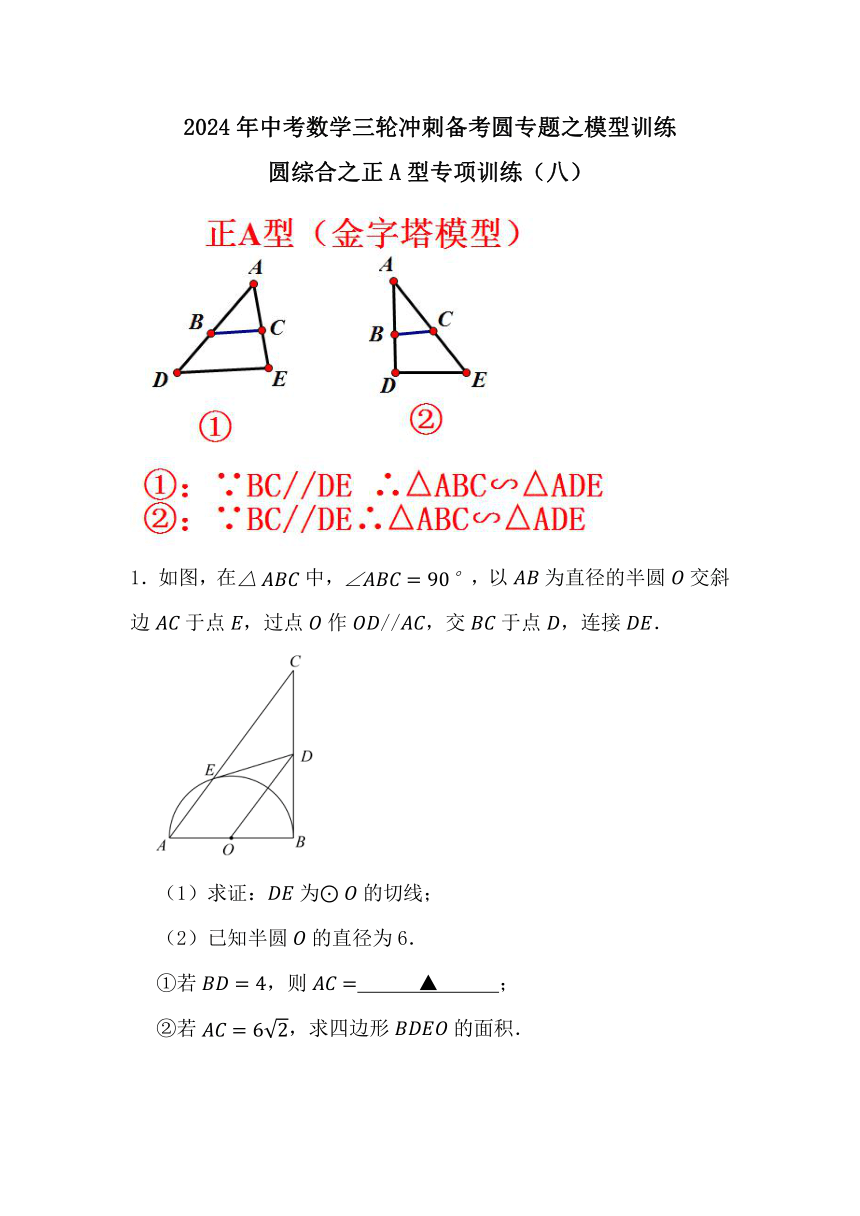 | |
| 格式 | docx | ||
| 文件大小 | 433.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-04 16:43:16 | ||
图片预览



文档简介
2024年中考数学三轮冲刺备考圆专题之模型训练
圆综合之正A型专项训练(八)
1.如图,在中,,以为直径的半圆交斜边于点,过点作//,交于点,连接.
(1)求证:为的切线;
(2)已知半圆的直径为6.
①若,则 ▲ ;
②若,求四边形的面积.
2.如图,已知的直径与弦相交于点E.且E为中点,过点B作交的延长线于点F.
(1)求证:是的切线.
(2)连接,若的半径为4,,求、的长.
3.如图所示,在中,,以AB为直径的⊙O与交于点D,过点D作于点F,交的延长线于E.
(1)判断直线与⊙O的位置关系,并说明理由;
(2)当,⊙O的直径为30时,求的长.
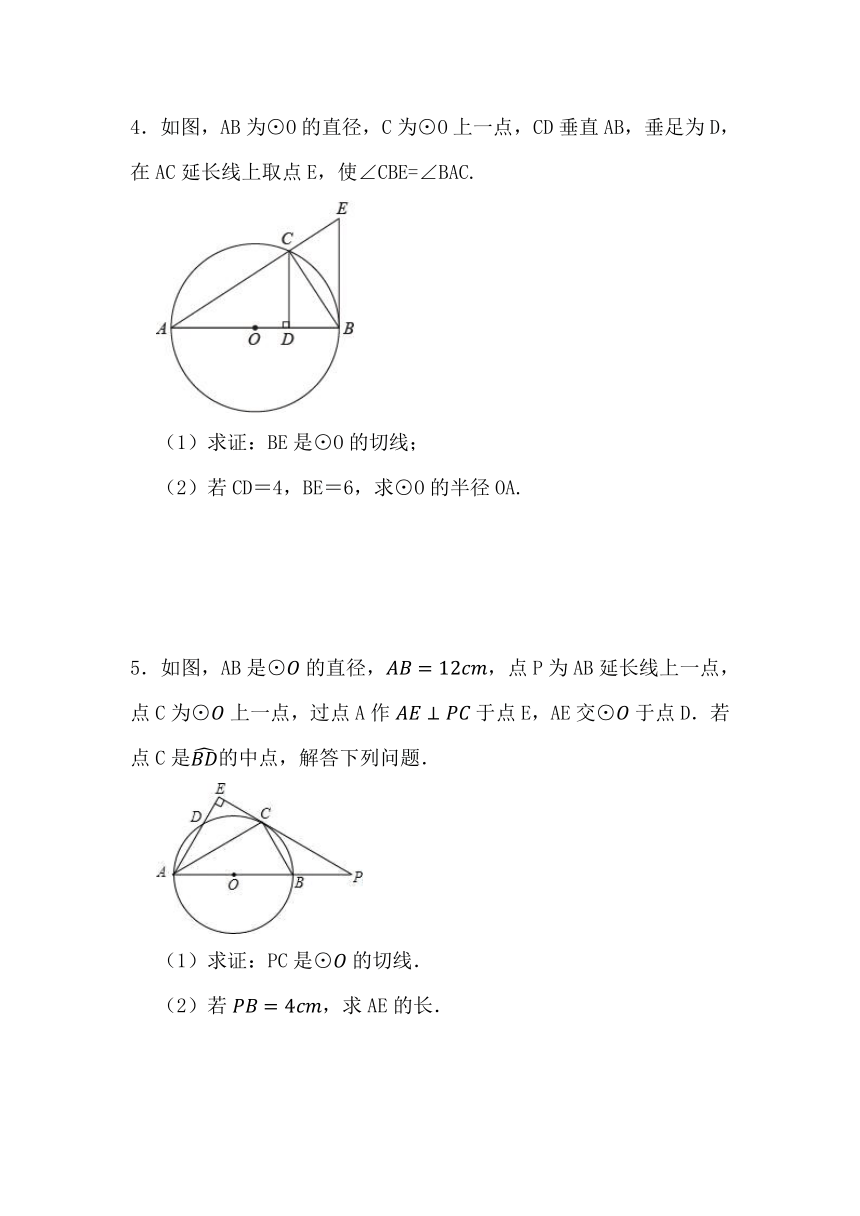
4.如图,AB为⊙O的直径,C为⊙O上一点,CD垂直AB,垂足为D,在AC延长线上取点E,使∠CBE=∠BAC.
(1)求证:BE是⊙O的切线;
(2)若CD=4,BE=6,求⊙O的半径OA.
5.如图,AB是⊙的直径,,点P为AB延长线上一点,点C为⊙上一点,过点A作于点E,AE交⊙于点D.若点C是的中点,解答下列问题.
(1)求证:PC是⊙的切线.
(2)若,求AE的长.
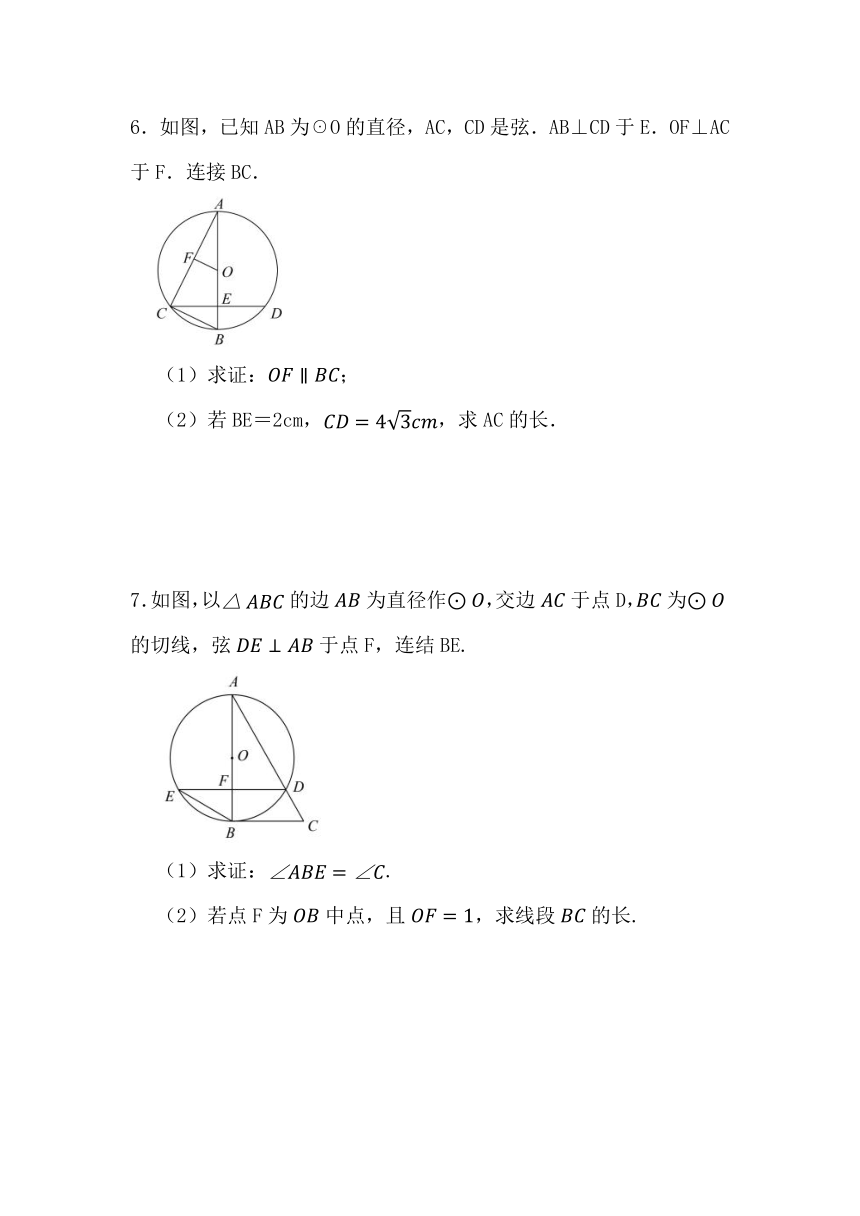
6.如图,已知AB为☉O的直径,AC,CD是弦.AB⊥CD于E.OF⊥AC于F.连接BC.
(1)求证:;
(2)若BE=2cm,,求AC的长.
7.如图,以的边为直径作,交边于点D,为的切线,弦于点F,连结BE.
(1)求证:.
(2)若点F为中点,且,求线段的长.
8.如图,四边形ABCD中,ADBC,AD⊥AB,AD=AB=1,DC=,以A为圆心,AD为半径作圆,延长CD交⊙A于点F,延长DA交⊙A于点E,连结BF,交DE于点G.
(1)求证:BC为⊙A的切线;
(2)求cos∠EDF的值;
(3)求线段BG的长.
9.已知:如图,AB是⊙O的直径,点D是AB延长线上一点,CD与⊙O相切于点E,连接AC交⊙O于点F,AE平分∠DAC.
(1)求证:AC⊥CD;
(2)若∠D=30°,AD=6,求AF的长.
10.如图,在中,,以AB为直径的交AC于点D,E是BC的中点,连接DE,BD.
(1)求证:DE是的切线;
(2)若,,求BD的长.
11.如图,AB为⊙O的直径,C为BA延长线上一点,D为⊙O上一点,OF⊥AD于点E,交CD于点F,且∠ADC=∠AOF.
(1)求证:CD与⊙O相切于点D;
(2)若sin∠C=,BD=12,求EF的长.
12.如图, 与 的AB,AC边分别相切于点D、C,与BC边交于点E,CE是 的直径.
(1)求证: .
(2)若 ,求BE的长.
13.如图,在△ABC中,∠ACB=90°,D为AB边上一点,以AD为直径的⊙O分别交AC、BC边于点E、F,连接EF,OE,已知EF平分∠OEC,OE的延长线交BC的延长线于点G.
(1)求证:BC是⊙O的切线;
(2)若EG=5,CG=3,求线段AE的长.
14.如图,AB是⊙O的直径,C是⊙O上一点,过C作⊙O的切线交AB的延长线于点D,连接AC、BC,过O作OF∥AC,交BC于G,交DC于F.
(1)求证:∠DCB=∠DOF;
(2)若tan∠A= ,BC=4,求OF、DF的长.
参考答案
1.【答案】(1)证明:连接OE,
∵OD∥AC,
∴∠BOD=∠A,
∠EOD=∠AEO,
又∵OA=OE,
∴∠A=∠OEA,
∴∠DOB=∠DOE,
在△DOE和△DOB中,
∴△DOE≌△DOB,
∴∠DEO=∠DBO=90°,
∴DE为圆O的切线;
(2)解:①10;
②有①知AC=2OD,
∴OD= ,
在直角△BOD中,
BD= ,
∴S△BOD= ,
由(1)知△OED≌△OBD,
∴S△DOE= S△BOD=,
∴S四边形BDEO =9.
2.【答案】(1)证明:∵⊙O的直径AB与弦CD相交于点E,且E为CD中点,
∴∠AED=90°,
∵,
∴∠ABF=∠AED=90°,
∴AB⊥BF,
∵AB是⊙O的直径,
∴BF是⊙O的切线
(2)解:连接BD,CD,
∴∠BCD=∠BAD,
∵AB是⊙O的直径,
∴∠ADB=90°,
∵sin∠BAD=sin∠BCD=,
∴,
∴设BD=3x,AB=4x,
∴
∵⊙O的半径为4,
∴AB=8,
∴4x=8,
解得x=2 ,
∴AD=.
由
3.【答案】(1)解:直线与⊙O相切.
理由如下:
如图所示,连接OD.
∵OA=OD,
∴∠OAD=∠ADO.
∵∠DOE是△AOD的一个外角,
∴∠DOE=2∠A.
∵∠CBE=2∠A,
∴∠DOE=∠CBE.
∴OD//BC.
∵ DF⊥BC,
∴∠BFE=90°.
∴∠ODE =90°.
∴ OD⊥DE,
∵OD是⊙O的半径,
∴直线DE与⊙O相切.
(2)解:由(1)可知OD⊥DE,
∵DF⊥BC,
∴ OD∥BC.
∴△EFB∽△EDO.
∴.
在Rt△BEF中,
∵,设BF=3x,BE=5x.
∵AB=30,
∴OB=OD=15.
∴,
解得:x1=0,x2=2.
经检验x=2是原分式方程的解.
∴BF =3x=3×2=6.
4.【答案】(1)证明:∵AB为⊙O直径,
∴∠ACB=90°,
∴∠CAB+∠ABC=90°,
∵∠CBE=∠BAC,
∴∠ABC+∠CBE=90°,
∴∠ABE=90°,
∴BE是⊙O的切线;
(2)解:连接OC,
设OA=r,
∵∠CDA=∠ABE=90°,∠BAF=∠DAC,
∴△ADC∽△ABE,
∴,
∴,
∴,
在Rt△OCD中,OD2+CD5=OC2,
∴,
∵r>0,
∴,
∴OA=3.
5.【答案】(1)解:如图,连接OC,
∵点C是的中点,
∴∠DAC=∠CAB,
∵OA=OC,
∴∠CAB=∠ACO,
∴∠ACO=∠EAC,
∴OC//AE,
∵AE⊥PE,
∴∠OCP=∠AEP=90°,
∵OC为⊙半径,
∴PC是⊙的切线.
(2)解:∵AB=12,BP=4,
∴OC=OB=AB=6,OP=OB+BP=10,AP=AB+BP=16,
由(1)可知OC//AE,
∴△PCO∽△PEA,
∴,即,
解得:AE=.
6.【答案】(1)证明:∵AB为☉O的直径,
∴∠ACB=90°,即BC⊥AC,
又∵OF⊥AC,
∴.
(2)解:∵AB为☉O的直径,AB⊥CD,,
∴,
在中,由勾股定理得,
∵,,
∴,
∴,即,
解得;
∴的长为cm.
7.【答案】(1)证明 ∵AB是⊙O的直径,BC为⊙O的切线,
∴ABBC,
∵DE⊥AB,
∴DE//BC,
∴,
∵弧AE所对圆周角是和,
∴,
∴;
(2)解:连接OE,
∵点F为OB中点,ABBC,
∴=,
,
∴,
EF=FD=,
∴ AF=3,
,
∽,
∴,即,
得,.
8.【答案】(1)证明:∵AD⊥AB,
∴∠BAD=90°,
∵AD∥BC,
∴∠ABC=180°﹣∠BAD=90°,
∵AB=AD,
∴BC为⊙A的切线;
(2)解:如图1,过点D作DH⊥BC于H,
∠DHB=90°,由(1)知,∠BAD=∠ABC=90°,
∴∠ABC=∠BAD=∠BHD=90°,
∴四边形ABHD为矩形,
∵AB=AD=1,
∴矩形ABHD是正方形,
∴BH=DH=AB=1,
在Rt△DHC中,CD=,根据勾股定理得,CH==2,
∴cosC===,
∵AD∥BC,
∴∠EDF=∠C,
∴cos∠EDF=cosC=;
(3)解:如图2,
过点A作AM⊥DF于M,则DF=2DM,∠AMD=90°,
在Rt△AMD中,AD=1,cos∠EDF=,
∴DM=AD cos∠EDF=1×=,
∴DF=2DM=,
∴CF=DF+CD==,
∵AD∥BC,
∴△DFG∽△CFB,
∴,
由(2)知,BC=1+2=3,
∴=,
∴DG=,
∴AG=DG﹣AD=,
在Rt△BAG中,BG===.
9.【答案】(1)证明:如图,连接OE,
∵CD与⊙O相切于点E,
∴CD,
∵OE=OA,
∴∠OEA=∠OAE,
又AE平分∠DAC,
∴∠EAC=∠OAE,
∴∠OEA=∠EAC,
∴OEAC,
∴CD.
(2)解:如图,连接BF,
由(1)得CD,∠C=90°
又∵AB是⊙O的直径,
∴∠BFA=90°,
∴∠BFA=∠C,
∴BFCD,∠FBA=∠D=30°,
设⊙O的半径为r,
∵∠D=30°,由(1)得CD,
∴DO=2OE=2r,
AD=DO+AO=3r,
∵AD=6,
∴r=2.则AB=2r=4,
在Rt△BFA中,∠FBA=30° ,
AF=AB=2.
10.【答案】(1)证明:连接OD,如图所示,
∵AB为的直径,
∴,
∴,
∵点E为BC的中点,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
∵OD是的半径,
∴DE与相切;
(2)解:由(1)知,,
∵E是BC的中点,
∴,
∴,
∵,
∴.
11.【答案】(1)解:如图,连接OD,
∵OA=OD,
∴∠OAD=∠ODA,
∵OF⊥AD,
∴∠AEO=90°,
∴∠AOF+∠OAD=90°,
∵∠ADC=∠AOF,
∴∠ADC+∠ODA=90°,
即∠ODC=90°,
∴OD⊥CD,
∴CD与⊙O相切于点D;
(2)解:∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠ADB=∠AEO,
∴OF∥BD,OA=OB,
∴OE=BD=×12=6,
∵sinC=,
设OD=x,OC=3x,则OB=x,
∴CB=OC+OB=4x,
∵OF∥BD,
∴△COF∽△CBD,
∴,
∴,
∴OF=9,
∴EF=OF OE=9 6=3.
12.【答案】(1)证明:连接OD,
∵AB,AC是 的切线,
∴ , ,
∵ ,
∴ ,
∴ .
∵ ,
∴ ,
∴ .
(2)解:∵ ,
∴ ,
∴ ,
∵ ,
∴ ,
∴ .
∵ , ,
∴ ,
∴ ,即 ,
∴ ,
∴ .
13.【答案】(1)证明:连接OF,
∵EF平分∠OEC,
∴∠OEF=∠CEF,
又∵OE=OF,
∴∠OEF=∠OFE,
∴∠CEF=∠OEF=∠OFE,
∴OF AC,
∵∠ACB=90°,
∴∠OFC=90°,即:OF⊥BC,
又∵OF为半径,
∴BC是⊙O的切线;
(2)解:连接ED交OF于点H.
∵EG=5,CG=3,∠ECG=90°,
∴CE= =4,
∵AD是直径,
∴∠AED=90°,从而∠CEH=90°,
∴∠OFC=∠ACB=∠CEH=90°,
∴四边形CEHF是矩形,
∴HF=CE=4,且∠EHF=90°,
∴OF垂直平分弦ED,H为ED中点,
∵OF CE,
∴△GCE∽△GFO,
∴ ,
又∵OE=OF,GO=OE+EG,
∴有 ,
解得OF=20,
经检验,OF=20是分式方程的根,
∴OH=OF HF=20 4=16,
又∵在△AED中,点O和点H分别是AD和ED边的中点,
∴AE=2OH=32.
∴线段AE的长为32.
14.【答案】(1)证明:如图所示,连接OC,
∵CD是圆O的切线,AB是圆O的直径,
∴∠OCD=∠ACB=90°,
∴∠DCB+∠OCB=∠OCA+∠OCB,
∴∠DCB=∠OCA,
∵OC=OA,
∴∠OAC=∠OCA=∠DCB,
∵ ,
∴∠DOF=∠OAC,
∴∠DOF=∠DCB;
(2)解:设OF与BC交于点G,
∵ ,
∴△OBG∽△ABC,∠BGO=∠ACB=90°
∴ ,∠CGF=90°
∴ ,
∴CG=2,
∵∠BCD=∠OAC, ,
∴ ,
∴ ,
∴ , ,
∴ ,
同理可证△OFD∽△ACD,
∴ ,
∴ ,
∴ .
圆综合之正A型专项训练(八)
1.如图,在中,,以为直径的半圆交斜边于点,过点作//,交于点,连接.
(1)求证:为的切线;
(2)已知半圆的直径为6.
①若,则 ▲ ;
②若,求四边形的面积.
2.如图,已知的直径与弦相交于点E.且E为中点,过点B作交的延长线于点F.
(1)求证:是的切线.
(2)连接,若的半径为4,,求、的长.
3.如图所示,在中,,以AB为直径的⊙O与交于点D,过点D作于点F,交的延长线于E.
(1)判断直线与⊙O的位置关系,并说明理由;
(2)当,⊙O的直径为30时,求的长.
4.如图,AB为⊙O的直径,C为⊙O上一点,CD垂直AB,垂足为D,在AC延长线上取点E,使∠CBE=∠BAC.
(1)求证:BE是⊙O的切线;
(2)若CD=4,BE=6,求⊙O的半径OA.
5.如图,AB是⊙的直径,,点P为AB延长线上一点,点C为⊙上一点,过点A作于点E,AE交⊙于点D.若点C是的中点,解答下列问题.
(1)求证:PC是⊙的切线.
(2)若,求AE的长.
6.如图,已知AB为☉O的直径,AC,CD是弦.AB⊥CD于E.OF⊥AC于F.连接BC.
(1)求证:;
(2)若BE=2cm,,求AC的长.
7.如图,以的边为直径作,交边于点D,为的切线,弦于点F,连结BE.
(1)求证:.
(2)若点F为中点,且,求线段的长.
8.如图,四边形ABCD中,ADBC,AD⊥AB,AD=AB=1,DC=,以A为圆心,AD为半径作圆,延长CD交⊙A于点F,延长DA交⊙A于点E,连结BF,交DE于点G.
(1)求证:BC为⊙A的切线;
(2)求cos∠EDF的值;
(3)求线段BG的长.
9.已知:如图,AB是⊙O的直径,点D是AB延长线上一点,CD与⊙O相切于点E,连接AC交⊙O于点F,AE平分∠DAC.
(1)求证:AC⊥CD;
(2)若∠D=30°,AD=6,求AF的长.
10.如图,在中,,以AB为直径的交AC于点D,E是BC的中点,连接DE,BD.
(1)求证:DE是的切线;
(2)若,,求BD的长.
11.如图,AB为⊙O的直径,C为BA延长线上一点,D为⊙O上一点,OF⊥AD于点E,交CD于点F,且∠ADC=∠AOF.
(1)求证:CD与⊙O相切于点D;
(2)若sin∠C=,BD=12,求EF的长.
12.如图, 与 的AB,AC边分别相切于点D、C,与BC边交于点E,CE是 的直径.
(1)求证: .
(2)若 ,求BE的长.
13.如图,在△ABC中,∠ACB=90°,D为AB边上一点,以AD为直径的⊙O分别交AC、BC边于点E、F,连接EF,OE,已知EF平分∠OEC,OE的延长线交BC的延长线于点G.
(1)求证:BC是⊙O的切线;
(2)若EG=5,CG=3,求线段AE的长.
14.如图,AB是⊙O的直径,C是⊙O上一点,过C作⊙O的切线交AB的延长线于点D,连接AC、BC,过O作OF∥AC,交BC于G,交DC于F.
(1)求证:∠DCB=∠DOF;
(2)若tan∠A= ,BC=4,求OF、DF的长.
参考答案
1.【答案】(1)证明:连接OE,
∵OD∥AC,
∴∠BOD=∠A,
∠EOD=∠AEO,
又∵OA=OE,
∴∠A=∠OEA,
∴∠DOB=∠DOE,
在△DOE和△DOB中,
∴△DOE≌△DOB,
∴∠DEO=∠DBO=90°,
∴DE为圆O的切线;
(2)解:①10;
②有①知AC=2OD,
∴OD= ,
在直角△BOD中,
BD= ,
∴S△BOD= ,
由(1)知△OED≌△OBD,
∴S△DOE= S△BOD=,
∴S四边形BDEO =9.
2.【答案】(1)证明:∵⊙O的直径AB与弦CD相交于点E,且E为CD中点,
∴∠AED=90°,
∵,
∴∠ABF=∠AED=90°,
∴AB⊥BF,
∵AB是⊙O的直径,
∴BF是⊙O的切线
(2)解:连接BD,CD,
∴∠BCD=∠BAD,
∵AB是⊙O的直径,
∴∠ADB=90°,
∵sin∠BAD=sin∠BCD=,
∴,
∴设BD=3x,AB=4x,
∴
∵⊙O的半径为4,
∴AB=8,
∴4x=8,
解得x=2 ,
∴AD=.
由
3.【答案】(1)解:直线与⊙O相切.
理由如下:
如图所示,连接OD.
∵OA=OD,
∴∠OAD=∠ADO.
∵∠DOE是△AOD的一个外角,
∴∠DOE=2∠A.
∵∠CBE=2∠A,
∴∠DOE=∠CBE.
∴OD//BC.
∵ DF⊥BC,
∴∠BFE=90°.
∴∠ODE =90°.
∴ OD⊥DE,
∵OD是⊙O的半径,
∴直线DE与⊙O相切.
(2)解:由(1)可知OD⊥DE,
∵DF⊥BC,
∴ OD∥BC.
∴△EFB∽△EDO.
∴.
在Rt△BEF中,
∵,设BF=3x,BE=5x.
∵AB=30,
∴OB=OD=15.
∴,
解得:x1=0,x2=2.
经检验x=2是原分式方程的解.
∴BF =3x=3×2=6.
4.【答案】(1)证明:∵AB为⊙O直径,
∴∠ACB=90°,
∴∠CAB+∠ABC=90°,
∵∠CBE=∠BAC,
∴∠ABC+∠CBE=90°,
∴∠ABE=90°,
∴BE是⊙O的切线;
(2)解:连接OC,
设OA=r,
∵∠CDA=∠ABE=90°,∠BAF=∠DAC,
∴△ADC∽△ABE,
∴,
∴,
∴,
在Rt△OCD中,OD2+CD5=OC2,
∴,
∵r>0,
∴,
∴OA=3.
5.【答案】(1)解:如图,连接OC,
∵点C是的中点,
∴∠DAC=∠CAB,
∵OA=OC,
∴∠CAB=∠ACO,
∴∠ACO=∠EAC,
∴OC//AE,
∵AE⊥PE,
∴∠OCP=∠AEP=90°,
∵OC为⊙半径,
∴PC是⊙的切线.
(2)解:∵AB=12,BP=4,
∴OC=OB=AB=6,OP=OB+BP=10,AP=AB+BP=16,
由(1)可知OC//AE,
∴△PCO∽△PEA,
∴,即,
解得:AE=.
6.【答案】(1)证明:∵AB为☉O的直径,
∴∠ACB=90°,即BC⊥AC,
又∵OF⊥AC,
∴.
(2)解:∵AB为☉O的直径,AB⊥CD,,
∴,
在中,由勾股定理得,
∵,,
∴,
∴,即,
解得;
∴的长为cm.
7.【答案】(1)证明 ∵AB是⊙O的直径,BC为⊙O的切线,
∴ABBC,
∵DE⊥AB,
∴DE//BC,
∴,
∵弧AE所对圆周角是和,
∴,
∴;
(2)解:连接OE,
∵点F为OB中点,ABBC,
∴=,
,
∴,
EF=FD=,
∴ AF=3,
,
∽,
∴,即,
得,.
8.【答案】(1)证明:∵AD⊥AB,
∴∠BAD=90°,
∵AD∥BC,
∴∠ABC=180°﹣∠BAD=90°,
∵AB=AD,
∴BC为⊙A的切线;
(2)解:如图1,过点D作DH⊥BC于H,
∠DHB=90°,由(1)知,∠BAD=∠ABC=90°,
∴∠ABC=∠BAD=∠BHD=90°,
∴四边形ABHD为矩形,
∵AB=AD=1,
∴矩形ABHD是正方形,
∴BH=DH=AB=1,
在Rt△DHC中,CD=,根据勾股定理得,CH==2,
∴cosC===,
∵AD∥BC,
∴∠EDF=∠C,
∴cos∠EDF=cosC=;
(3)解:如图2,
过点A作AM⊥DF于M,则DF=2DM,∠AMD=90°,
在Rt△AMD中,AD=1,cos∠EDF=,
∴DM=AD cos∠EDF=1×=,
∴DF=2DM=,
∴CF=DF+CD==,
∵AD∥BC,
∴△DFG∽△CFB,
∴,
由(2)知,BC=1+2=3,
∴=,
∴DG=,
∴AG=DG﹣AD=,
在Rt△BAG中,BG===.
9.【答案】(1)证明:如图,连接OE,
∵CD与⊙O相切于点E,
∴CD,
∵OE=OA,
∴∠OEA=∠OAE,
又AE平分∠DAC,
∴∠EAC=∠OAE,
∴∠OEA=∠EAC,
∴OEAC,
∴CD.
(2)解:如图,连接BF,
由(1)得CD,∠C=90°
又∵AB是⊙O的直径,
∴∠BFA=90°,
∴∠BFA=∠C,
∴BFCD,∠FBA=∠D=30°,
设⊙O的半径为r,
∵∠D=30°,由(1)得CD,
∴DO=2OE=2r,
AD=DO+AO=3r,
∵AD=6,
∴r=2.则AB=2r=4,
在Rt△BFA中,∠FBA=30° ,
AF=AB=2.
10.【答案】(1)证明:连接OD,如图所示,
∵AB为的直径,
∴,
∴,
∵点E为BC的中点,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
∵OD是的半径,
∴DE与相切;
(2)解:由(1)知,,
∵E是BC的中点,
∴,
∴,
∵,
∴.
11.【答案】(1)解:如图,连接OD,
∵OA=OD,
∴∠OAD=∠ODA,
∵OF⊥AD,
∴∠AEO=90°,
∴∠AOF+∠OAD=90°,
∵∠ADC=∠AOF,
∴∠ADC+∠ODA=90°,
即∠ODC=90°,
∴OD⊥CD,
∴CD与⊙O相切于点D;
(2)解:∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠ADB=∠AEO,
∴OF∥BD,OA=OB,
∴OE=BD=×12=6,
∵sinC=,
设OD=x,OC=3x,则OB=x,
∴CB=OC+OB=4x,
∵OF∥BD,
∴△COF∽△CBD,
∴,
∴,
∴OF=9,
∴EF=OF OE=9 6=3.
12.【答案】(1)证明:连接OD,
∵AB,AC是 的切线,
∴ , ,
∵ ,
∴ ,
∴ .
∵ ,
∴ ,
∴ .
(2)解:∵ ,
∴ ,
∴ ,
∵ ,
∴ ,
∴ .
∵ , ,
∴ ,
∴ ,即 ,
∴ ,
∴ .
13.【答案】(1)证明:连接OF,
∵EF平分∠OEC,
∴∠OEF=∠CEF,
又∵OE=OF,
∴∠OEF=∠OFE,
∴∠CEF=∠OEF=∠OFE,
∴OF AC,
∵∠ACB=90°,
∴∠OFC=90°,即:OF⊥BC,
又∵OF为半径,
∴BC是⊙O的切线;
(2)解:连接ED交OF于点H.
∵EG=5,CG=3,∠ECG=90°,
∴CE= =4,
∵AD是直径,
∴∠AED=90°,从而∠CEH=90°,
∴∠OFC=∠ACB=∠CEH=90°,
∴四边形CEHF是矩形,
∴HF=CE=4,且∠EHF=90°,
∴OF垂直平分弦ED,H为ED中点,
∵OF CE,
∴△GCE∽△GFO,
∴ ,
又∵OE=OF,GO=OE+EG,
∴有 ,
解得OF=20,
经检验,OF=20是分式方程的根,
∴OH=OF HF=20 4=16,
又∵在△AED中,点O和点H分别是AD和ED边的中点,
∴AE=2OH=32.
∴线段AE的长为32.
14.【答案】(1)证明:如图所示,连接OC,
∵CD是圆O的切线,AB是圆O的直径,
∴∠OCD=∠ACB=90°,
∴∠DCB+∠OCB=∠OCA+∠OCB,
∴∠DCB=∠OCA,
∵OC=OA,
∴∠OAC=∠OCA=∠DCB,
∵ ,
∴∠DOF=∠OAC,
∴∠DOF=∠DCB;
(2)解:设OF与BC交于点G,
∵ ,
∴△OBG∽△ABC,∠BGO=∠ACB=90°
∴ ,∠CGF=90°
∴ ,
∴CG=2,
∵∠BCD=∠OAC, ,
∴ ,
∴ ,
∴ , ,
∴ ,
同理可证△OFD∽△ACD,
∴ ,
∴ ,
∴ .
同课章节目录
