高二数学大单元整体学习学程《第二章 直线与圆》学案(无答案)
文档属性
| 名称 | 高二数学大单元整体学习学程《第二章 直线与圆》学案(无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 736.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-03 00:00:00 | ||
图片预览




文档简介
《空间几何体》大单元整体学习学程 班级:________小组:________ 姓名:_______评价:__________
高二数学
大单元整体学习学程
直线与圆
班级:
小组:
姓名:
第八单元:直线与圆
单元概述
【学科大概念】
利用点的坐标,刻画几何对象,研究几何对象的性质以及探讨几何对象之间的关系。
【课程大概念】
建立平面直角坐标系,依托对方程和几何性质的研究,揭示解析几何的本质,发展数学抽象和数学建模能力,初步形成研究解析几何的一般思路即用代数方法解决几何问题。
【单元内容】
坐标法、直线及其方程、圆及其方程、两直线位置关系、两圆的位置关系、直线与圆的位置关系。
【课标要求】
1.直线与方程
(1)在平面直角坐标系中,结合具体图形,探索确定直线位置的几何要素。
(2)理解直线的倾斜角和斜率的概念,经历用代数方法刻画直线斜率的过程,掌握过两点的直线斜率的计算公式。
(3)能根据斜率判定两条直线平行或垂直。
(4)根据确定直线位置的几何要素,探索并掌握直线方程的几种形式(点斜式、两点式及一般式)。
(5)能用解方程组的方法求两条直线的交点坐标。
(6)探索并掌握平面上两点间的距离公式、点到直线的距离公式,会求两条平行直线间的距离。
2.圆与方程
(1)回顾确定圆的几何要素,在平面直角坐标系中,探索并掌握圆的标准方程与一般方程。
(2)能根据给定直线、圆的方程,判断直线与圆、圆与圆的位置关系。
(3)能用直线和圆的方程解决一些简单的数学问题与实际问题。
【单元目标】
1.类比数轴上的点与实数的对应关系,确立点、直线、曲线几何性质的研究方法,能用坐标法表述直线方程、圆的方程,初步接触解析几何的思想。
2.探索空间中两直线位置关系、圆与圆的位置关系、直线与圆的位置,并能用代数法刻画这三种位置关系,形成数与形问题的相互转化能力。
3.结合实际问题,建立数学模型,运用坐标法解决解析几何的核心问题,提升数学建模和数学抽象的数学核心素养。
4.从直线方程、圆的方程、直线与圆的位置关系重构单元结构,掌握解析几何的基本思想和方法即借助数和形的对应关系建立曲线方程,把形的问题转化为数的研究,再把数的研究转化为形来讨论。
【评价预设】
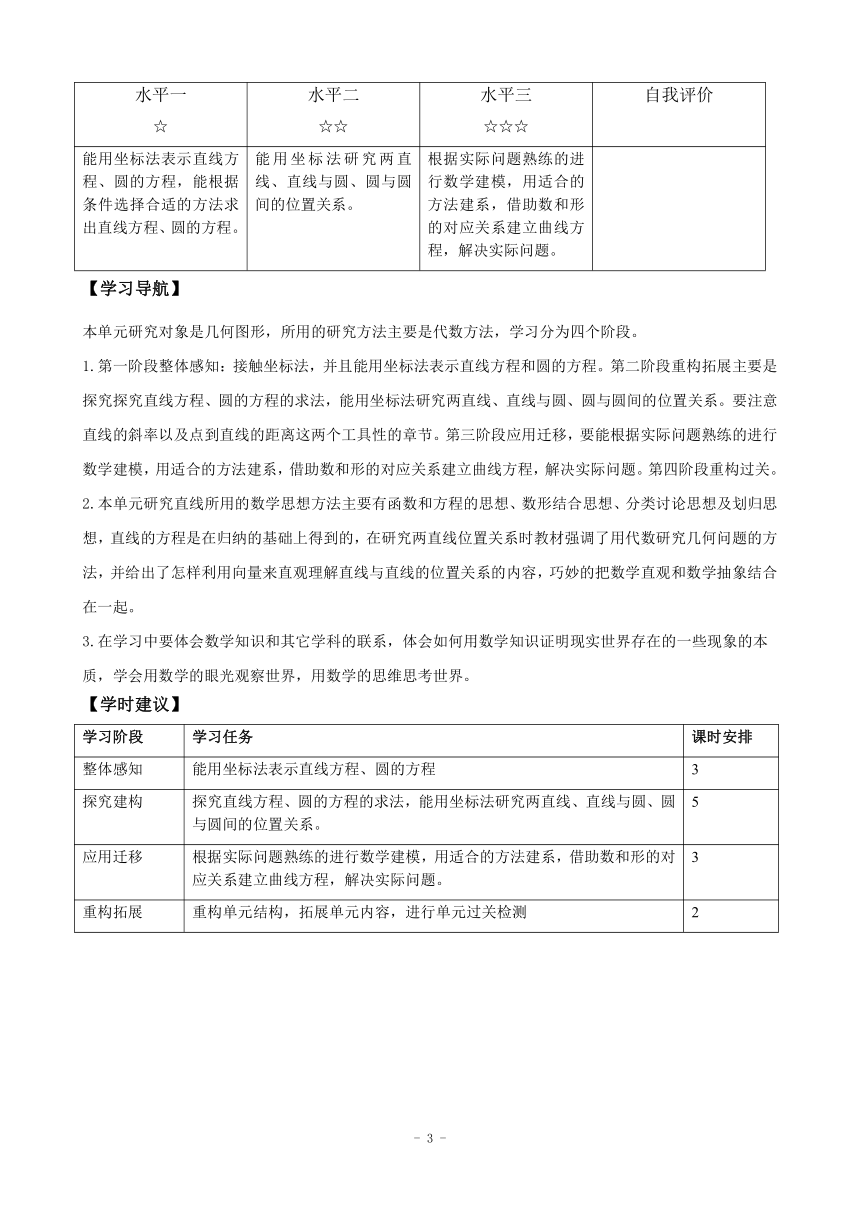
水平一 ☆ 水平二 ☆☆ 水平三 ☆☆☆ 自我评价
能用坐标法表示直线方程、圆的方程,能根据条件选择合适的方法求出直线方程、圆的方程。 能用坐标法研究两直线、直线与圆、圆与圆间的位置关系。 根据实际问题熟练的进行数学建模,用适合的方法建系,借助数和形的对应关系建立曲线方程,解决实际问题。
【学习导航】
本单元研究对象是几何图形,所用的研究方法主要是代数方法,学习分为四个阶段。
1.第一阶段整体感知:接触坐标法,并且能用坐标法表示直线方程和圆的方程。第二阶段重构拓展主要是探究探究直线方程、圆的方程的求法,能用坐标法研究两直线、直线与圆、圆与圆间的位置关系。要注意直线的斜率以及点到直线的距离这两个工具性的章节。第三阶段应用迁移,要能根据实际问题熟练的进行数学建模,用适合的方法建系,借助数和形的对应关系建立曲线方程,解决实际问题。第四阶段重构过关。
2.本单元研究直线所用的数学思想方法主要有函数和方程的思想、数形结合思想、分类讨论思想及划归思想,直线的方程是在归纳的基础上得到的,在研究两直线位置关系时教材强调了用代数研究几何问题的方法,并给出了怎样利用向量来直观理解直线与直线的位置关系的内容,巧妙的把数学直观和数学抽象结合在一起。
3.在学习中要体会数学知识和其它学科的联系,体会如何用数学知识证明现实世界存在的一些现象的本质,学会用数学的眼光观察世界,用数学的思维思考世界。
【学时建议】
学习阶段 学习任务 课时安排
整体感知 能用坐标法表示直线方程、圆的方程 3
探究建构 探究直线方程、圆的方程的求法,能用坐标法研究两直线、直线与圆、圆与圆间的位置关系。 5
应用迁移 根据实际问题熟练的进行数学建模,用适合的方法建系,借助数和形的对应关系建立曲线方程,解决实际问题。 3
重构拓展 重构单元结构,拓展单元内容,进行单元过关检测 2
直线与圆
----探究解析几何的研究路径
【学习目标】
1.类比向量的坐标表示,探索平面直角坐标系中的两点间的距离公式和中点坐标公式,说出坐标法解决平面几何问题的简便性。
2.经历对直线、圆两种几何图形的直观感知到坐标刻画过程,能表述直线方程、圆的方程。
3.通过对直线的方程、圆的方程的概念获得过程的研究,体验感悟概念的本质内涵。
【学习任务】探究解析几何的研究路径
—类比向量的坐标表示将直线与圆放到平面直角坐标系中
问题1:回顾必修四所学内容,与同小组的同学说一说如何运用坐标表示向量,如何计算向量的模。
问题2:借助向量的模计算公式推导出在平面直角坐标系中计算两点间的距离,借助向量的坐标表示推导出平面直角坐标系两点间的中点坐标公式。
问题3:借助平面直角坐标系解决以下问题:
已知ABCD是一个长方形,且M是ABCD所在平面上任意一个点,求证:.
--探究直线的基本要素并表示出直线方程
小明同学周末去逛超市,在乘坐自动扶梯的时候,发现超市里有从一楼直达二楼和直达三楼的两种电梯,若超市的层高相同,水平宽度相同,你能用数学的知识来解释这两种扶梯的区别吗?
问题1:(1)上述情境中容易看出,两种扶梯的倾斜程度不同.如果将一个扶梯看作一条直线,你如何描述它的倾斜程度呢?倾斜角的范围是什么?
、
(2)在生活中,我们常用“升高量与前进量的比”表示倾斜面的“坡度”(倾斜程度),则坡度的公式是怎样?并结合倾斜角,抽象出直线斜率的概念及表示方法.
问题2:设是平面直角坐标系中的直线,分别满足下列条件的是否唯一.如果唯一,作出相应的直线,并思考直线上任意一点的坐标应该满足什么条件.
(1)已知的斜率不存在;
(2)已知的斜率不存在且过点;
(3)已知的斜率为;
(4)已知的斜率为且经过点.
问题3:写出满足下列条件的直线的方程.
①经过点(3,2),斜率为; ②在轴上的截距为2,斜率为-1;
③经过点(-2,1)且垂直于轴; ④在轴上的截距为2,且与轴平行;
⑤在,轴上的截距分别是4,-3; ⑥经过A(-1,8),B(4,-2)两点.
——探究确定圆的几何要素并推导圆的方程
摩天轮从建成以来之所以能一直吸引众多的爱好者,除了寻找刺激之外,还因为它独特而五彩缤纷的外观,你能用数学语言来描述它的外观美吗?
问题1:探究圆的标准方程
1.在乘坐摩天轮的时候,我们的座椅在旋转的过程中会画出一个圆形,我们是如何定义这个图形的?那确定图形的几何要素是什么?哪个几何要素决定了圆的大小?哪个几何要素决定了圆的位置?
2.根据圆的定义中蕴含的确定圆的几何要素,怎样从动点轨迹的角度理解圆的定义?
3.在平面直角坐标系中,表示出圆心为,半径为的点的集合.
问题2:探究圆的一般方程
1.圆的标准方程是关于的二元二次方程,而二元二次方程都表示圆吗?
2.把圆的标准方程左边展开,如果令,则这个方程变成了怎样的形式?有什么特点?
【形成性评价1】
请你自己选择一个曲线,按照解析几何研究的思路来阐述你怎样研究这一曲线。
直线与圆
-----解决直线与圆的综合问题
【学习目标】
1.探索直线方程五种形式的区别与联系,能求直线方程;类比直线方程的求法,探索圆的方程的两种求解方法并进行比较;
2.从具体情境中抽象并探究两直线位置关系、两圆位置关系、直线与圆位置关系的代数刻画,说出对代数方法研究几何问题的理解;
3.经历几何问题代数化的过程,掌握解析几何方法,解决直线与圆的综合问题。
【情境任务】解决直线与圆的综合问题
——探究直线方程的求法
问题1.如果已知a=(u,v)为直线的一个方向向量,你能由此写出的斜率k和倾斜角吗?
问题2.在平面直角坐标系中,给定一个点和斜率,如何推导出直线的点斜式方程?
问题3.直线的斜截式方程是什么?直线的斜截式方程和直线的点斜式方程什么关系?直线的斜截式方程和一次函数的表达式有什么联系和区别?
问题4.直线经过与,直线的方程是什么?写出推导过程.
问题5.直线在轴上的截距是如何定义的?直线在上截距分别为,且,写出直线的方程.
问题6.写出直线的一般式方程.它可以表示平面直角坐标系上的任意直线吗?
【学习评测】
1.直线经过点P(2,3),且在x,y轴上的截距相等,试求该直线的方程.
2.求经过两条直线l1:2x+y-8=0和l2:x-2y+1=0的交点且与两坐标轴围成的三角形面积为的直线l的方程.
----探究圆的方程的求法
某施工队要建一座圆拱桥,其跨度为20m, 拱高为4m.已知一条满载货物的集装箱船,该船及货物离水面的高度是2米,船4米,问该船能否通过该桥?若能,那么船在什么区域内可通过?若不能,说明理由.
【归纳生成】
总结用圆的标准方程解决实际问题的活动经验.
【学习评测】
1.已知圆心在直线y=-4x上,且圆与直线l:x+y-1=0相切于点P(3,-2),则该圆的方程是________________.
2.已知三点A(1,0),B(0,),C(2,),则△ABC外接圆的圆心到原点的距离为________.
3.已知以点P为圆心的圆经过点A(-1,0)和B(3,4),线段AB的垂直平分线交圆P于点C和D,且|CD|=4.
(1)求直线CD的方程;
(2)求圆P的方程.
----探究直线与直线的位置关系
在初中我们已经明确在同一平面内,两直线的位置关系主要有相交、平行和重合,那么我们能否通过直线的斜率,用代数方法来判断平面上两条直线的位置关系呢?
问题1.设两条直线的斜率分别为.当时,与满足什么关系?请写出推导过程.
问题2.设两条直线的斜率分别为.当时,与满足什么关系?请写出推导过程.
问题3.如何判断斜率不存在的直线的位置关系.
问题4.已知两条直线的方程为,则下列系数满足什么条件,使得相交、平行、垂直?
【归纳生成】
归纳出判断两直线平行、相交、垂直的方法.
【学习评测】
1.已知直线方程::2x-4y+7=0,:x-2y+5=0,则与的关系是_________.
2.若点A(0,1),B(,4)在直线上,直线⊥,则的倾斜角为________.
3.下列直线中,能够与直线x+3y+4=0相交的直线是________.
①x+3y=1;②3x+y=0;③+=1;④y=-x+4.
---探究点到直线的距离
类比空间中点到直线的距离,你能想办法求出到直线的距离吗?写出求解过程.
问题1.如何求点到直线的距离?写出研究过程.
问题2.你能用向量的数量积推导点到直线的距离公式吗?写出推导过程.
【归纳生成】
用向量研究点到直线距离的思路.
【学习评测】
1.求下列点到直线的距离
(1) (2)
2.在轴上与的距离等于5的点的坐标是 .
3.两直线与之间的距离是 .
---探究直线与圆的位置关系
《使至塞上》
王维
单车欲问边,属国过居延.
征蓬出汉塞,归雁入胡天.
大漠孤烟直,长河落日圆.
萧关逢候骑,都护在燕然.
第三句以出色的描写,道出了边塞之景的奇特壮丽和作者的孤寂之感.诗中的夕阳在西落的过程中,与地平线的位置关系有哪几种,请用图形语言描述.那你的分类依据又是什么?
问题1.我们已经知道,在平面直角坐标系中,直线和圆都可以用方程来表示,一个点是否在直线或圆上,只要看这个点的坐标是否满足他们的方程即可。那么能否利用直线与圆的方程来研究它们之间的位置关系呢?请尝试用代数法判断直线与圆的位置关系。
问题2. 如何利用几何法研究直线与圆的位置关系?
【归纳生成】
归纳直线与圆位置关系的判定方法.
【学习评测】
1.过原点且倾斜角为的直线被圆所截得的弦长为 .
2.已知过点的直线被圆所截得的弦长为,求直线的方程.
---探究圆与圆的位置关系
观察下面生活中常见的图形,感受圆与圆之间有哪些位置关系?
问题1.圆与圆位置关系有哪几种?如何刻画这几种关系?
问题2.类比直线与圆的位置关系判断方法,思考如何用代数法与几何法判断两圆的位置关系?
【归纳生成】
归纳判断圆与圆位置关系的方法.
【学习评测】
1.已知圆交于A、B两点,则AB所在的直线方程是_______________.
2.已知和,则这两圆的公共弦长为 .
3.已知圆和圆相交于A、B两点,求:(1)公共弦AB所在直线的方程 (2)公共弦的长度.
【形成性评价2】
评价标准1:用两种方法求直线方程、圆的方程
评价问题:直线经过直线和的交点,且在两坐标轴上的截距相等,求直线的方程.
评价标准2:两直线的位置关系求参数
评价问题:已知直线,求满足下列条件的的取值.
(1) 相交 (2) 平行 (3) 重合
评价标准3:直线与圆的位置关系解决综合问题
评价问题:已知直线与圆C:交于A、B两点。
(1)求线段AB的垂直平分线的方程;
(2)若,求的值
(3)在(2)的条件下,求过点的圆C的切线方程
直线与圆
-- --运用代数法解决平面几何的核心问题
【学习目标】
1.运用代数法解决平面几何的核心问题,举实例说明代数法和几何法的异同及转化策略;
2.从实际问题情境中抽象出解析几何模型,解决直线与圆的位置关系问题;
3.通过问题的解决提升直观想象、数学建模和数学抽象的数学核心素养。
【情境任务】运用代数法解决平面几何的核心问题
----点到直线的距离
某仓库附近有一条铁路,现需要修一条公路把仓库和铁路连接起来,为了节约成本,距离越短费用越低,现将铁路看成一条直线,应如何求出仓库到铁路的最短距离?
问题1:设仓库的坐标为,铁路所在直线方程为,如何求点到直线的最短距离,尝试写出求解过程?
问题2:验证当时,问题1中的公式是否成立?
问题3:建立适当的坐标系,可得仓库所在位置的坐标为,铁路所在直线方程为,求出仓库到铁路的最短距离?
----直线与圆的方程在平面几何中的应用
已知内接于圆的四边形的对角线互相垂直,求证:圆心到一边的距离等于这条边所对边长的一半.
问题1:许多平面几何问题常利用“坐标法”来解决,首先要做的工作是建立适当的直角坐标系,在本题中应如何选取坐标系?
问题2:如图所示建立直角坐标系,设四边形的四个顶点分别为点A(a,0),B(0,b),C(c,0),D(0,d),那么BC边的长为多少?
问题3:四边形ABCD的外接圆圆心M的坐标如何?
问题4:如何计算圆心M到直线AD的距离|MN|?
问题5:由上述计算可得|BC|=2|MN|,从而命题成立.你能用平面几何知识证明这个命题吗?
----直线与圆的方程在实际生活中的应用
一艘轮船在沿直线返回港口的途中,接到气象台的台风预报:台风中心位于轮船正西70 km处, 受影响的范围是半径长为30km的圆形区域. 已知港口位于台风中心正北40 km处,如果这艘轮船不改变航线,那么它是否会受到台风的影响?
问题1:你有什么办法判断轮船航线是否经过台风圆域?
问题2:如图所示建立直角坐标系,取10km为长度单位,那么轮船航线所在直线和台风圆域边界所在圆的方程分别是什么?
问题3:直线4x+7y-28=0与圆x2+y2=9的位置关系如何?对问题1应作怎样的回答?
【学习评测】
如图是某圆拱形桥一孔圆拱的示意图. 这个圆的圆拱跨度AB=20m,拱高OP=4m,建造时每间隔4m需要用一根支柱支撑,求支柱A2P2的高度(精确到0.01m)
你能用几何法求支柱A2P2的高度吗?
如图所示建立直角坐标系,那么求支柱A2P2的高度,化归为求一个什么问题?
取1m为长度单位,如何求圆拱所在圆的方程?
利用这个圆的方程可求得点P2的纵坐标是多少?问题Ⅱ的答案如何?
【形成性评价3】
评价标准1:能够利用直线和圆方程解决几何问题
评价问题:(1)求直线l: 2x-y-2=0被圆C: (x-3)2+y2=0所截得的弦长.
(2)已知圆C:x2+y2-4x-6y+12=0,点A(3,5).
(1)求过点A的圆的切线方程;
(2)O点是坐标原点,连接OA,OC,求△AOC的面积S.
评价标准2:能够利用直线和圆方程解决实际问题
评价问题: 一个小岛的周围有环岛暗礁,暗礁分布以小岛的中心为圆心,半径30km的圆形区域.已知小岛中心位于轮船正西70km处,港口位于小岛中心正北40km处,如果轮船沿直线返航,那么它是否会有触礁危险
直线与圆
---应用代数法解决解析几何中的综合问题
【学习目标】
1.结合271bay中的学习资源,从直线与圆的几何要素、方程、关系三个方面构建单元知识与逻辑体系。
2.能够掌握平面解析几何解决问题的基本过程,体会数学学习中的类比、由特殊到一般等探索的学习方式。
3.类比直线方程、圆的方程的求法,探索出三种圆锥曲线的方程,深刻理解解析几何思想。
【单元重构】
从直线方程、圆的方程、位置关系等方面层层深入,再次阅读《直线与圆》的课本内容及271BAY相关资源,梳理本单元的核心知识和它们逻辑体系,重构思维导图.
【单元拓展】
学习了解析几何解决问题的方法后,我们能熟练地建立坐标系求出直线方程和圆的方程,并能研究两者的位置关系。请大家按照下面的要求动手操作,给出切割后得到了什么曲线?能不能类比求出这些曲线的方程?
(1)当平面与圆锥面的母线平行,且不过圆锥顶点;
(2)当平面只与圆锥面一侧相交,且不过圆锥顶点;
(3)当平面只与圆锥面一侧相交,且不过圆锥顶点,并与圆锥面的对称轴垂直;
(4)当平面与圆锥面两侧都相交,且不过圆锥顶点,结果为双曲线的一支(另一支为此圆锥面的对顶圆锥面与平面的交线);
【单元过关】
——求直线方程、圆的方程
1.已知点A(-7,4),点B(-5,6),则线段AB的垂直平分线的方程 ________________________.
2.已知直线过点且其法向量为,则其方程为 ;已知直线过点且其方向向量为,则其方程为 .
——直线与圆位置关系的应用
3.已知圆心在直线y=-4x上,且圆与直线l:x+y-1=0相切于点P(3,-2),则该圆的方程是________________.
4.已知三点A(1,0),B(0,),C(2,),则△ABC外接圆的圆心到原点的距离为________.
5.已知以点P为圆心的圆经过点A(-1,0)和B(3,4),线段AB的垂直平分线交圆P于点C和D,且|CD|=4.
(1)求直线CD的方程;
(2)求圆P的方程.
形成性评价4
水平划分 水平标准 自我评价
水平一 从直线与圆的几何要素、方程、关系三个方面构建单元知识与逻辑体系
水平二 能够掌握平面解析几何解决问题的基本过程,体会数学学习中的类比、由特殊到一般等探索的学习方式。
水平三 类比直线方程、圆的方程的求法,探索出三种圆锥曲线的方程,深刻理解解析几何思想。
单元检测
一、选择题:
1. 直线的倾斜角为( )
A. B. C. D.
2.将直线绕原点逆时针旋转,再向右平移1个单位,所得到的直线为( )
A. B. C. D.
3.直线与圆相切,则实数等于( )
A.或 B.或 C.或 D.或
4.过点的直线与圆相交于,两点,则的最小值为( )
A.2 B. C.3 D.
5.若圆C的半径为1,圆心在第一象限,且与直线和x轴都相切,则该圆的标准
方程是( )
A. B.
C. D.
6.已知圆:+=1,圆与圆关于直线对称,则圆的方
程为( )
A.+=1 B.+=1
C.+=1 D.+=1
7.已知圆C与直线 及都相切,圆心在直线上,则圆C的
方程为( )
A. B.
C. D.
8.设在轴上,它到点的距离等于到点的距离的两倍,那么点的坐标是( )
A.(1,0,0)和( -1,0,0) B.(2,0,0)和(-2,0,0)
C.(,0,0)和(,0,0) D.(,0,0)和(,0,0)
9.直线被圆所截得的弦长为( )
A. B. C. D.
10.若直线与曲线有公共点,则b的取值范围是( )
A.[,] B.[,3] C.[-1,] D.[,3]
二、填空题:
11.设若圆与圆的公共弦长为,则=______.
12.已知圆过点,且圆心在轴的正半轴上,直线被该圆所截得的弦长为,则圆的标准方程为_________ ___.
13.已知圆的圆心与点关于直线对称.直线与圆相
交于两点,且,则圆的方程为 .
14.已知直线与直线 平行,则 .
15.直线被两平行线所截得的线段的长为,则的
倾斜角可以是①;②;③;④;⑤. 其中正确答案的序号是 .
三、解答题:
16(1).已知圆C经过A(5,1),B(1,3)两点,圆心在x轴上,求圆C的方程.
.(2)求与圆同心,且与直线相切的圆的方程.
17.已知圆,
(Ⅰ)若直线过定点(1,0),且与圆相切,求的方程;
(Ⅱ) 若圆的半径为3,圆心在直线:上,且与圆外切,求圆的方程.
18.在平面直角坐标系xOy中,已知圆C1:(x+3)2+(y-1)2=4和圆C2:(x-4)2+(y-5)2=9.
(1)判断两圆的位置关系;
(2)求直线m的方程,使直线m被圆C1截得的弦长为4,与圆C截得的弦长是6.
19.已知圆C: 直线
(1)证明:不论取何实数,直线与圆C恒相交;
(2)求直线被圆C所截得的弦长的最小值及此时直线的方程;
20.已知以点C (t∈R,t≠0)为圆心的圆与x轴交于点O、A,与y轴交于点O、B,其中O为原点.
(1)求证:△AOB的面积为定值;
(2)设直线2x+y-4=0与圆C交于点M、N,若OM=ON,求圆C的方程;
21.在平面直角坐标系中,已知圆 的圆心为,过点且斜率为的直线与圆相交于不同的两点.
(Ⅰ)求的取值范围;
(Ⅱ)以OA,OB为邻边作平行四边形OADB,是否存在常数,使得直线OD与PQ平行如果存在,求值;如果不存在,请说明理由.
高二数学
大单元整体学习学程
直线与圆
班级:
小组:
姓名:
第八单元:直线与圆
单元概述
【学科大概念】
利用点的坐标,刻画几何对象,研究几何对象的性质以及探讨几何对象之间的关系。
【课程大概念】
建立平面直角坐标系,依托对方程和几何性质的研究,揭示解析几何的本质,发展数学抽象和数学建模能力,初步形成研究解析几何的一般思路即用代数方法解决几何问题。
【单元内容】
坐标法、直线及其方程、圆及其方程、两直线位置关系、两圆的位置关系、直线与圆的位置关系。
【课标要求】
1.直线与方程
(1)在平面直角坐标系中,结合具体图形,探索确定直线位置的几何要素。
(2)理解直线的倾斜角和斜率的概念,经历用代数方法刻画直线斜率的过程,掌握过两点的直线斜率的计算公式。
(3)能根据斜率判定两条直线平行或垂直。
(4)根据确定直线位置的几何要素,探索并掌握直线方程的几种形式(点斜式、两点式及一般式)。
(5)能用解方程组的方法求两条直线的交点坐标。
(6)探索并掌握平面上两点间的距离公式、点到直线的距离公式,会求两条平行直线间的距离。
2.圆与方程
(1)回顾确定圆的几何要素,在平面直角坐标系中,探索并掌握圆的标准方程与一般方程。
(2)能根据给定直线、圆的方程,判断直线与圆、圆与圆的位置关系。
(3)能用直线和圆的方程解决一些简单的数学问题与实际问题。
【单元目标】
1.类比数轴上的点与实数的对应关系,确立点、直线、曲线几何性质的研究方法,能用坐标法表述直线方程、圆的方程,初步接触解析几何的思想。
2.探索空间中两直线位置关系、圆与圆的位置关系、直线与圆的位置,并能用代数法刻画这三种位置关系,形成数与形问题的相互转化能力。
3.结合实际问题,建立数学模型,运用坐标法解决解析几何的核心问题,提升数学建模和数学抽象的数学核心素养。
4.从直线方程、圆的方程、直线与圆的位置关系重构单元结构,掌握解析几何的基本思想和方法即借助数和形的对应关系建立曲线方程,把形的问题转化为数的研究,再把数的研究转化为形来讨论。
【评价预设】
水平一 ☆ 水平二 ☆☆ 水平三 ☆☆☆ 自我评价
能用坐标法表示直线方程、圆的方程,能根据条件选择合适的方法求出直线方程、圆的方程。 能用坐标法研究两直线、直线与圆、圆与圆间的位置关系。 根据实际问题熟练的进行数学建模,用适合的方法建系,借助数和形的对应关系建立曲线方程,解决实际问题。
【学习导航】
本单元研究对象是几何图形,所用的研究方法主要是代数方法,学习分为四个阶段。
1.第一阶段整体感知:接触坐标法,并且能用坐标法表示直线方程和圆的方程。第二阶段重构拓展主要是探究探究直线方程、圆的方程的求法,能用坐标法研究两直线、直线与圆、圆与圆间的位置关系。要注意直线的斜率以及点到直线的距离这两个工具性的章节。第三阶段应用迁移,要能根据实际问题熟练的进行数学建模,用适合的方法建系,借助数和形的对应关系建立曲线方程,解决实际问题。第四阶段重构过关。
2.本单元研究直线所用的数学思想方法主要有函数和方程的思想、数形结合思想、分类讨论思想及划归思想,直线的方程是在归纳的基础上得到的,在研究两直线位置关系时教材强调了用代数研究几何问题的方法,并给出了怎样利用向量来直观理解直线与直线的位置关系的内容,巧妙的把数学直观和数学抽象结合在一起。
3.在学习中要体会数学知识和其它学科的联系,体会如何用数学知识证明现实世界存在的一些现象的本质,学会用数学的眼光观察世界,用数学的思维思考世界。
【学时建议】
学习阶段 学习任务 课时安排
整体感知 能用坐标法表示直线方程、圆的方程 3
探究建构 探究直线方程、圆的方程的求法,能用坐标法研究两直线、直线与圆、圆与圆间的位置关系。 5
应用迁移 根据实际问题熟练的进行数学建模,用适合的方法建系,借助数和形的对应关系建立曲线方程,解决实际问题。 3
重构拓展 重构单元结构,拓展单元内容,进行单元过关检测 2
直线与圆
----探究解析几何的研究路径
【学习目标】
1.类比向量的坐标表示,探索平面直角坐标系中的两点间的距离公式和中点坐标公式,说出坐标法解决平面几何问题的简便性。
2.经历对直线、圆两种几何图形的直观感知到坐标刻画过程,能表述直线方程、圆的方程。
3.通过对直线的方程、圆的方程的概念获得过程的研究,体验感悟概念的本质内涵。
【学习任务】探究解析几何的研究路径
—类比向量的坐标表示将直线与圆放到平面直角坐标系中
问题1:回顾必修四所学内容,与同小组的同学说一说如何运用坐标表示向量,如何计算向量的模。
问题2:借助向量的模计算公式推导出在平面直角坐标系中计算两点间的距离,借助向量的坐标表示推导出平面直角坐标系两点间的中点坐标公式。
问题3:借助平面直角坐标系解决以下问题:
已知ABCD是一个长方形,且M是ABCD所在平面上任意一个点,求证:.
--探究直线的基本要素并表示出直线方程
小明同学周末去逛超市,在乘坐自动扶梯的时候,发现超市里有从一楼直达二楼和直达三楼的两种电梯,若超市的层高相同,水平宽度相同,你能用数学的知识来解释这两种扶梯的区别吗?
问题1:(1)上述情境中容易看出,两种扶梯的倾斜程度不同.如果将一个扶梯看作一条直线,你如何描述它的倾斜程度呢?倾斜角的范围是什么?
、
(2)在生活中,我们常用“升高量与前进量的比”表示倾斜面的“坡度”(倾斜程度),则坡度的公式是怎样?并结合倾斜角,抽象出直线斜率的概念及表示方法.
问题2:设是平面直角坐标系中的直线,分别满足下列条件的是否唯一.如果唯一,作出相应的直线,并思考直线上任意一点的坐标应该满足什么条件.
(1)已知的斜率不存在;
(2)已知的斜率不存在且过点;
(3)已知的斜率为;
(4)已知的斜率为且经过点.
问题3:写出满足下列条件的直线的方程.
①经过点(3,2),斜率为; ②在轴上的截距为2,斜率为-1;
③经过点(-2,1)且垂直于轴; ④在轴上的截距为2,且与轴平行;
⑤在,轴上的截距分别是4,-3; ⑥经过A(-1,8),B(4,-2)两点.
——探究确定圆的几何要素并推导圆的方程
摩天轮从建成以来之所以能一直吸引众多的爱好者,除了寻找刺激之外,还因为它独特而五彩缤纷的外观,你能用数学语言来描述它的外观美吗?
问题1:探究圆的标准方程
1.在乘坐摩天轮的时候,我们的座椅在旋转的过程中会画出一个圆形,我们是如何定义这个图形的?那确定图形的几何要素是什么?哪个几何要素决定了圆的大小?哪个几何要素决定了圆的位置?
2.根据圆的定义中蕴含的确定圆的几何要素,怎样从动点轨迹的角度理解圆的定义?
3.在平面直角坐标系中,表示出圆心为,半径为的点的集合.
问题2:探究圆的一般方程
1.圆的标准方程是关于的二元二次方程,而二元二次方程都表示圆吗?
2.把圆的标准方程左边展开,如果令,则这个方程变成了怎样的形式?有什么特点?
【形成性评价1】
请你自己选择一个曲线,按照解析几何研究的思路来阐述你怎样研究这一曲线。
直线与圆
-----解决直线与圆的综合问题
【学习目标】
1.探索直线方程五种形式的区别与联系,能求直线方程;类比直线方程的求法,探索圆的方程的两种求解方法并进行比较;
2.从具体情境中抽象并探究两直线位置关系、两圆位置关系、直线与圆位置关系的代数刻画,说出对代数方法研究几何问题的理解;
3.经历几何问题代数化的过程,掌握解析几何方法,解决直线与圆的综合问题。
【情境任务】解决直线与圆的综合问题
——探究直线方程的求法
问题1.如果已知a=(u,v)为直线的一个方向向量,你能由此写出的斜率k和倾斜角吗?
问题2.在平面直角坐标系中,给定一个点和斜率,如何推导出直线的点斜式方程?
问题3.直线的斜截式方程是什么?直线的斜截式方程和直线的点斜式方程什么关系?直线的斜截式方程和一次函数的表达式有什么联系和区别?
问题4.直线经过与,直线的方程是什么?写出推导过程.
问题5.直线在轴上的截距是如何定义的?直线在上截距分别为,且,写出直线的方程.
问题6.写出直线的一般式方程.它可以表示平面直角坐标系上的任意直线吗?
【学习评测】
1.直线经过点P(2,3),且在x,y轴上的截距相等,试求该直线的方程.
2.求经过两条直线l1:2x+y-8=0和l2:x-2y+1=0的交点且与两坐标轴围成的三角形面积为的直线l的方程.
----探究圆的方程的求法
某施工队要建一座圆拱桥,其跨度为20m, 拱高为4m.已知一条满载货物的集装箱船,该船及货物离水面的高度是2米,船4米,问该船能否通过该桥?若能,那么船在什么区域内可通过?若不能,说明理由.
【归纳生成】
总结用圆的标准方程解决实际问题的活动经验.
【学习评测】
1.已知圆心在直线y=-4x上,且圆与直线l:x+y-1=0相切于点P(3,-2),则该圆的方程是________________.
2.已知三点A(1,0),B(0,),C(2,),则△ABC外接圆的圆心到原点的距离为________.
3.已知以点P为圆心的圆经过点A(-1,0)和B(3,4),线段AB的垂直平分线交圆P于点C和D,且|CD|=4.
(1)求直线CD的方程;
(2)求圆P的方程.
----探究直线与直线的位置关系
在初中我们已经明确在同一平面内,两直线的位置关系主要有相交、平行和重合,那么我们能否通过直线的斜率,用代数方法来判断平面上两条直线的位置关系呢?
问题1.设两条直线的斜率分别为.当时,与满足什么关系?请写出推导过程.
问题2.设两条直线的斜率分别为.当时,与满足什么关系?请写出推导过程.
问题3.如何判断斜率不存在的直线的位置关系.
问题4.已知两条直线的方程为,则下列系数满足什么条件,使得相交、平行、垂直?
【归纳生成】
归纳出判断两直线平行、相交、垂直的方法.
【学习评测】
1.已知直线方程::2x-4y+7=0,:x-2y+5=0,则与的关系是_________.
2.若点A(0,1),B(,4)在直线上,直线⊥,则的倾斜角为________.
3.下列直线中,能够与直线x+3y+4=0相交的直线是________.
①x+3y=1;②3x+y=0;③+=1;④y=-x+4.
---探究点到直线的距离
类比空间中点到直线的距离,你能想办法求出到直线的距离吗?写出求解过程.
问题1.如何求点到直线的距离?写出研究过程.
问题2.你能用向量的数量积推导点到直线的距离公式吗?写出推导过程.
【归纳生成】
用向量研究点到直线距离的思路.
【学习评测】
1.求下列点到直线的距离
(1) (2)
2.在轴上与的距离等于5的点的坐标是 .
3.两直线与之间的距离是 .
---探究直线与圆的位置关系
《使至塞上》
王维
单车欲问边,属国过居延.
征蓬出汉塞,归雁入胡天.
大漠孤烟直,长河落日圆.
萧关逢候骑,都护在燕然.
第三句以出色的描写,道出了边塞之景的奇特壮丽和作者的孤寂之感.诗中的夕阳在西落的过程中,与地平线的位置关系有哪几种,请用图形语言描述.那你的分类依据又是什么?
问题1.我们已经知道,在平面直角坐标系中,直线和圆都可以用方程来表示,一个点是否在直线或圆上,只要看这个点的坐标是否满足他们的方程即可。那么能否利用直线与圆的方程来研究它们之间的位置关系呢?请尝试用代数法判断直线与圆的位置关系。
问题2. 如何利用几何法研究直线与圆的位置关系?
【归纳生成】
归纳直线与圆位置关系的判定方法.
【学习评测】
1.过原点且倾斜角为的直线被圆所截得的弦长为 .
2.已知过点的直线被圆所截得的弦长为,求直线的方程.
---探究圆与圆的位置关系
观察下面生活中常见的图形,感受圆与圆之间有哪些位置关系?
问题1.圆与圆位置关系有哪几种?如何刻画这几种关系?
问题2.类比直线与圆的位置关系判断方法,思考如何用代数法与几何法判断两圆的位置关系?
【归纳生成】
归纳判断圆与圆位置关系的方法.
【学习评测】
1.已知圆交于A、B两点,则AB所在的直线方程是_______________.
2.已知和,则这两圆的公共弦长为 .
3.已知圆和圆相交于A、B两点,求:(1)公共弦AB所在直线的方程 (2)公共弦的长度.
【形成性评价2】
评价标准1:用两种方法求直线方程、圆的方程
评价问题:直线经过直线和的交点,且在两坐标轴上的截距相等,求直线的方程.
评价标准2:两直线的位置关系求参数
评价问题:已知直线,求满足下列条件的的取值.
(1) 相交 (2) 平行 (3) 重合
评价标准3:直线与圆的位置关系解决综合问题
评价问题:已知直线与圆C:交于A、B两点。
(1)求线段AB的垂直平分线的方程;
(2)若,求的值
(3)在(2)的条件下,求过点的圆C的切线方程
直线与圆
-- --运用代数法解决平面几何的核心问题
【学习目标】
1.运用代数法解决平面几何的核心问题,举实例说明代数法和几何法的异同及转化策略;
2.从实际问题情境中抽象出解析几何模型,解决直线与圆的位置关系问题;
3.通过问题的解决提升直观想象、数学建模和数学抽象的数学核心素养。
【情境任务】运用代数法解决平面几何的核心问题
----点到直线的距离
某仓库附近有一条铁路,现需要修一条公路把仓库和铁路连接起来,为了节约成本,距离越短费用越低,现将铁路看成一条直线,应如何求出仓库到铁路的最短距离?
问题1:设仓库的坐标为,铁路所在直线方程为,如何求点到直线的最短距离,尝试写出求解过程?
问题2:验证当时,问题1中的公式是否成立?
问题3:建立适当的坐标系,可得仓库所在位置的坐标为,铁路所在直线方程为,求出仓库到铁路的最短距离?
----直线与圆的方程在平面几何中的应用
已知内接于圆的四边形的对角线互相垂直,求证:圆心到一边的距离等于这条边所对边长的一半.
问题1:许多平面几何问题常利用“坐标法”来解决,首先要做的工作是建立适当的直角坐标系,在本题中应如何选取坐标系?
问题2:如图所示建立直角坐标系,设四边形的四个顶点分别为点A(a,0),B(0,b),C(c,0),D(0,d),那么BC边的长为多少?
问题3:四边形ABCD的外接圆圆心M的坐标如何?
问题4:如何计算圆心M到直线AD的距离|MN|?
问题5:由上述计算可得|BC|=2|MN|,从而命题成立.你能用平面几何知识证明这个命题吗?
----直线与圆的方程在实际生活中的应用
一艘轮船在沿直线返回港口的途中,接到气象台的台风预报:台风中心位于轮船正西70 km处, 受影响的范围是半径长为30km的圆形区域. 已知港口位于台风中心正北40 km处,如果这艘轮船不改变航线,那么它是否会受到台风的影响?
问题1:你有什么办法判断轮船航线是否经过台风圆域?
问题2:如图所示建立直角坐标系,取10km为长度单位,那么轮船航线所在直线和台风圆域边界所在圆的方程分别是什么?
问题3:直线4x+7y-28=0与圆x2+y2=9的位置关系如何?对问题1应作怎样的回答?
【学习评测】
如图是某圆拱形桥一孔圆拱的示意图. 这个圆的圆拱跨度AB=20m,拱高OP=4m,建造时每间隔4m需要用一根支柱支撑,求支柱A2P2的高度(精确到0.01m)
你能用几何法求支柱A2P2的高度吗?
如图所示建立直角坐标系,那么求支柱A2P2的高度,化归为求一个什么问题?
取1m为长度单位,如何求圆拱所在圆的方程?
利用这个圆的方程可求得点P2的纵坐标是多少?问题Ⅱ的答案如何?
【形成性评价3】
评价标准1:能够利用直线和圆方程解决几何问题
评价问题:(1)求直线l: 2x-y-2=0被圆C: (x-3)2+y2=0所截得的弦长.
(2)已知圆C:x2+y2-4x-6y+12=0,点A(3,5).
(1)求过点A的圆的切线方程;
(2)O点是坐标原点,连接OA,OC,求△AOC的面积S.
评价标准2:能够利用直线和圆方程解决实际问题
评价问题: 一个小岛的周围有环岛暗礁,暗礁分布以小岛的中心为圆心,半径30km的圆形区域.已知小岛中心位于轮船正西70km处,港口位于小岛中心正北40km处,如果轮船沿直线返航,那么它是否会有触礁危险
直线与圆
---应用代数法解决解析几何中的综合问题
【学习目标】
1.结合271bay中的学习资源,从直线与圆的几何要素、方程、关系三个方面构建单元知识与逻辑体系。
2.能够掌握平面解析几何解决问题的基本过程,体会数学学习中的类比、由特殊到一般等探索的学习方式。
3.类比直线方程、圆的方程的求法,探索出三种圆锥曲线的方程,深刻理解解析几何思想。
【单元重构】
从直线方程、圆的方程、位置关系等方面层层深入,再次阅读《直线与圆》的课本内容及271BAY相关资源,梳理本单元的核心知识和它们逻辑体系,重构思维导图.
【单元拓展】
学习了解析几何解决问题的方法后,我们能熟练地建立坐标系求出直线方程和圆的方程,并能研究两者的位置关系。请大家按照下面的要求动手操作,给出切割后得到了什么曲线?能不能类比求出这些曲线的方程?
(1)当平面与圆锥面的母线平行,且不过圆锥顶点;
(2)当平面只与圆锥面一侧相交,且不过圆锥顶点;
(3)当平面只与圆锥面一侧相交,且不过圆锥顶点,并与圆锥面的对称轴垂直;
(4)当平面与圆锥面两侧都相交,且不过圆锥顶点,结果为双曲线的一支(另一支为此圆锥面的对顶圆锥面与平面的交线);
【单元过关】
——求直线方程、圆的方程
1.已知点A(-7,4),点B(-5,6),则线段AB的垂直平分线的方程 ________________________.
2.已知直线过点且其法向量为,则其方程为 ;已知直线过点且其方向向量为,则其方程为 .
——直线与圆位置关系的应用
3.已知圆心在直线y=-4x上,且圆与直线l:x+y-1=0相切于点P(3,-2),则该圆的方程是________________.
4.已知三点A(1,0),B(0,),C(2,),则△ABC外接圆的圆心到原点的距离为________.
5.已知以点P为圆心的圆经过点A(-1,0)和B(3,4),线段AB的垂直平分线交圆P于点C和D,且|CD|=4.
(1)求直线CD的方程;
(2)求圆P的方程.
形成性评价4
水平划分 水平标准 自我评价
水平一 从直线与圆的几何要素、方程、关系三个方面构建单元知识与逻辑体系
水平二 能够掌握平面解析几何解决问题的基本过程,体会数学学习中的类比、由特殊到一般等探索的学习方式。
水平三 类比直线方程、圆的方程的求法,探索出三种圆锥曲线的方程,深刻理解解析几何思想。
单元检测
一、选择题:
1. 直线的倾斜角为( )
A. B. C. D.
2.将直线绕原点逆时针旋转,再向右平移1个单位,所得到的直线为( )
A. B. C. D.
3.直线与圆相切,则实数等于( )
A.或 B.或 C.或 D.或
4.过点的直线与圆相交于,两点,则的最小值为( )
A.2 B. C.3 D.
5.若圆C的半径为1,圆心在第一象限,且与直线和x轴都相切,则该圆的标准
方程是( )
A. B.
C. D.
6.已知圆:+=1,圆与圆关于直线对称,则圆的方
程为( )
A.+=1 B.+=1
C.+=1 D.+=1
7.已知圆C与直线 及都相切,圆心在直线上,则圆C的
方程为( )
A. B.
C. D.
8.设在轴上,它到点的距离等于到点的距离的两倍,那么点的坐标是( )
A.(1,0,0)和( -1,0,0) B.(2,0,0)和(-2,0,0)
C.(,0,0)和(,0,0) D.(,0,0)和(,0,0)
9.直线被圆所截得的弦长为( )
A. B. C. D.
10.若直线与曲线有公共点,则b的取值范围是( )
A.[,] B.[,3] C.[-1,] D.[,3]
二、填空题:
11.设若圆与圆的公共弦长为,则=______.
12.已知圆过点,且圆心在轴的正半轴上,直线被该圆所截得的弦长为,则圆的标准方程为_________ ___.
13.已知圆的圆心与点关于直线对称.直线与圆相
交于两点,且,则圆的方程为 .
14.已知直线与直线 平行,则 .
15.直线被两平行线所截得的线段的长为,则的
倾斜角可以是①;②;③;④;⑤. 其中正确答案的序号是 .
三、解答题:
16(1).已知圆C经过A(5,1),B(1,3)两点,圆心在x轴上,求圆C的方程.
.(2)求与圆同心,且与直线相切的圆的方程.
17.已知圆,
(Ⅰ)若直线过定点(1,0),且与圆相切,求的方程;
(Ⅱ) 若圆的半径为3,圆心在直线:上,且与圆外切,求圆的方程.
18.在平面直角坐标系xOy中,已知圆C1:(x+3)2+(y-1)2=4和圆C2:(x-4)2+(y-5)2=9.
(1)判断两圆的位置关系;
(2)求直线m的方程,使直线m被圆C1截得的弦长为4,与圆C截得的弦长是6.
19.已知圆C: 直线
(1)证明:不论取何实数,直线与圆C恒相交;
(2)求直线被圆C所截得的弦长的最小值及此时直线的方程;
20.已知以点C (t∈R,t≠0)为圆心的圆与x轴交于点O、A,与y轴交于点O、B,其中O为原点.
(1)求证:△AOB的面积为定值;
(2)设直线2x+y-4=0与圆C交于点M、N,若OM=ON,求圆C的方程;
21.在平面直角坐标系中,已知圆 的圆心为,过点且斜率为的直线与圆相交于不同的两点.
(Ⅰ)求的取值范围;
(Ⅱ)以OA,OB为邻边作平行四边形OADB,是否存在常数,使得直线OD与PQ平行如果存在,求值;如果不存在,请说明理由.
