数学好玩同步练习 北师大版数学五年级下册(含解析)
文档属性
| 名称 | 数学好玩同步练习 北师大版数学五年级下册(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 357.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-03 14:34:05 | ||
图片预览





文档简介
数学好玩
(共24题,满分100分)
题号 一 二 三 四 总分
得分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.注意书写整洁
一、选择题
1.下面的展开图折叠后所围成的图形是( )。
A. B. C.
2.两盒糖果包成一包,( )种包装方法最节省包装纸。
A. B. C.
3.把4个长8厘米,宽6厘米,高4厘米的长方体盒子(如图),包装成一个大长方体礼盒,下面最节约包装纸的是( )。
A. B. C.
4.下面的平面图形中,不能围成长方体或正方体的是( )。
A. B. C.
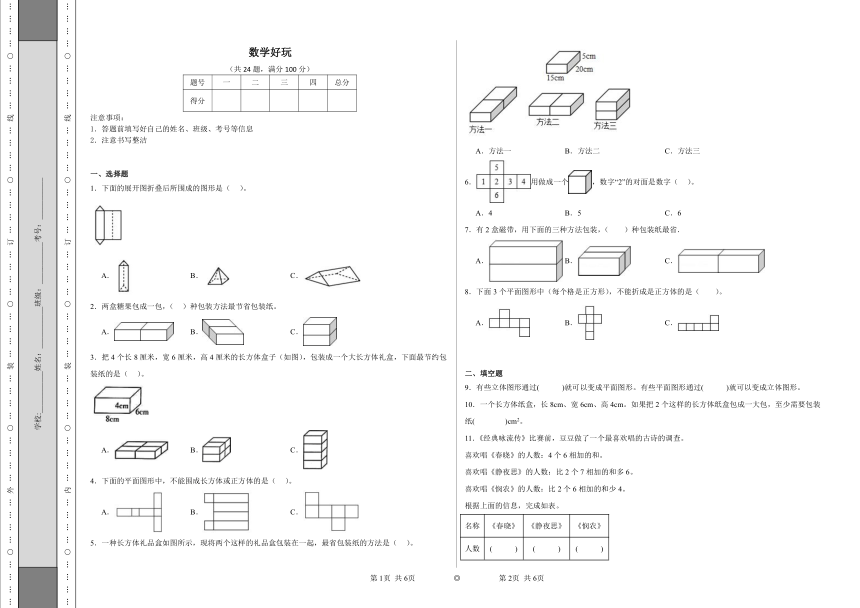
5.一种长方体礼品盒如图所示,现将两个这样的礼品盒包装在一起,最省包装纸的方法是( )。
A.方法一 B.方法二 C.方法三
6.用做成一个,数字“2”的对面是数字( )。
A.4 B.5 C.6
7.有2盒磁带,用下面的三种方法包装,( )种包装纸最省.
A. B. C.
8.下面3个平面图形中(每个格是正方形),不能折成是正方体的是( )。
A. B. C.
二、填空题
9.有些立体图形通过( )就可以变成平面图形。有些平面图形通过( )就可以变成立体图形。
10.一个长方体纸盒,长8cm、宽6cm、高4cm。如果把2个这样的长方体纸盒包成一大包,至少需要包装纸( )cm2。
11.《经典咏流传》比赛前,豆豆做了一个最喜欢唱的古诗的调查。
喜欢唱《春晓》的人数:4个6相加的和。
喜欢唱《静夜思》的人数:比2个7相加的和多6。
喜欢唱《悯农》的人数:比2个6相加的和少4。
根据上面的信息,完成如表。
名称 《春晓》 《静夜思》 《悯农》
人数 ( ) ( ) ( )
12.将下图按虚线折叠成一个封闭的立体图形,它的形状像什么?
分析与解答:它的形状像( )。
观察上图,房顶的侧面是边长分别为2cm、2cm、3cm的三角形,房子的侧面是长4cm、宽3cm的长方形,这两个长方形夹着的长8cm、宽4cm的大长方形就是小房子的正面。
13.下面是二(1)班同学体育课上参加体育活动的情况。
(1)参加( )的人数最多,参加( )的人数最少。
(2)参加跳绳的同学比参加跳远的多( )人。
(3)你还发现了什么?
(4)如果每个表示2个同学,上面的数据应该是多少?填一填。
活动 跳绳 踢球 跳远 踢毽子
人数 ( ) ( ) ( ) ( )
14.下面是二(3)班同学最喜欢的图书情况。
图书名称 《二年级的小豆豆》 《格林童话》 《昆虫记》 《父与子》 《成语故事》
人数 正 正 正正正 正正一 正
(1)把上面的统计结果填在如表中。
图书名称 《二年级的小豆豆》 《格林童话》 《昆虫记》 《父与子》 《成语故事》
人数
(2)最喜欢( )的人数最多,最喜欢( )的人数最少。
(3)最喜欢《昆虫记》的比最喜欢《父与子》的多( )人。
(4)这个班一共( )人。
15.将一个棱长为8cm的正方体分成两个相同的长方体,表面积增加了( )cm2。
三、判断题
16.如果1+2x=15,那么13x﹣7x=30。( )
17.用长7厘米、宽4厘米的长方形纸能折出一个周长是16厘米的正方形。( )
18.、、都不能折成一个无盖的正方体。( )
19.七巧板中没有平行四边形这个图形.( )
四、解决问题
20.小明和芳芳去爬山。
21.小娟和小军在校门口分手。8分钟后他们同时到家,小娟平均每分钟走42m,小军平均每分钟走多少米?
22.李阿姨带着陈阿姨去体验洛阳王城大道快速路。洛阳王城大道快速路通车前小汽车从龙门高铁站到北郊机场走王城大道需要0.5小时,每小时行40千米。通车后(公路全长不变),她俩乘小汽车从龙门高铁站到北郊机场走王城大道快速路,每小时行80千米,需要多少小时?
23.一辆客车从甲城开往乙城两城相距195千米。在前1.5小时的时间里平均每小时行82千米,剩下的路程0.8小时行完。平均每小时需行多少千米?
24.在5月的第二个星期日是母亲节。母亲节这天,张亮为妈妈买了礼物,他按下面的方法给礼品盒扎丝带,打结处用去丝带20厘米。
(1)扎这个礼品盒用去丝带多少厘米?
(2)制作这样一个礼品盒,至少需要纸板多少平方厘米?(接缝处忽略不计)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
) (
学校:___________姓名:___________班级:___________考号:___________
) (
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
第1页 共4页 ◎ 第2页 共4页
第1页 共4页 ◎ 第2页 共4页
参考答案:
1.A
【分析】根据展开图可知,围成的图形的上下面是两个相同的三角形,侧面是由3个长方形组成,也就是一个三棱柱,据此选择。
【详解】由分析可知,展开图折叠后所围成的图形是。
故选择:A
【点睛】此题考查了图形的展开与折叠,培养了学生的空间想象能力。
2.C
【分析】首先搞清是求长方体的表面积.要求怎样包装才能节约包装纸,应使这两盒糖果接触的面积最大,也就是说让最大面结合在一起,据此解答即可。
【详解】由分析可知:
将两盒糖包装成一包,最省包装纸的方案是C。
故答案为:C
【点睛】这是一道长方体表面积的实际应用,考查了学生对长方体表面积计算公式的掌握情况,以及实际操作能力。
3.B
【分析】求出选项中各长方体的长、宽、高,利用“长方体的表面积=(长×宽+宽×高+长×高)×2”求出长方体的表面积,最后比较大小,据此解答。
【详解】A.长:8×2=16(厘米)
宽:6×2=12(厘米)
高:4厘米
(16×12+16×4+12×4)×2
=(192+64+48)×2
=304×2
=608(平方厘米)
B.长:8厘米
宽:6×2=12(厘米)
高:4×2=8(厘米)
(8×12+8×8+12×8)×2
=(96+64+96)×2
=256×2
=512(平方厘米)
C.长:8厘米
宽:6厘米
高:4×4=16(厘米)
(8×6+8×16+6×16)×2
=(48+128+96)×2
=272×2
=544(平方厘米)
因为512平方厘米<544平方厘米<608平方厘米,所以最节约包装纸的是。
故答案为:B
【点睛】本题主要考查了包装问题,掌握长方体的表面积计算公式是解答题目的关键。
4.B
【分析】通过空间想象,一一分析,找出不能围成长方体或正方体的平面图形。
【详解】A.能围成一个长方体;
B.不能围成长方体或正方体;
C.能围成一个正方体。
故答案为:B
【点睛】本题考查了长方体或正方体的展开图,有一定空间想象力是解题的关键。
5.C
【分析】将两个礼品盒包装在一起,最省包装纸的方法是:把长方体中最大的面覆盖起来。这样包装在一起后表面积最小,即最省包装纸。
【详解】观察长方体礼品盒,结合长方体礼品盒长宽高数据可知,长方体的上、下面面积最大,则方法三最省包装纸。
故答案为:C
【点睛】求几个盒子包装在一起最省包装纸的方法,使包装好的图形表面积最小即可。
6.A
【分析】根据正方体展开图的11种特征,左面的平面图属于正方体展开图的“1-4-1”型,折成正方体后,数字“1”与“3”相对,“2”与“4”相对,“5”与“6”相对。
【详解】用做成一个,数字“2”的对面是数字“4”。
故答案为:A。
【点睛】正方体展开图分四种类型,11种情况,每种情况折成正方体后哪些面相对是有规律的,可自己动手操作一下并记住,能快速解答此类题。
7.A
【详解】试题分析:要想更省包装纸,需使表面积最小,由题意可知:只要让磁带的最大面露出的尽量少,则其表面积就会小,也就更能省包装纸,据此即可作出正确选择.
解:由图意可知:选项A露出的最大面最少,则其表面积最小,
所以A最省包装纸;
故选A.
点评:解答此题的关键是明白:要想更省包装纸,需使表面积最小,本题中,只要让磁带的最大面露出的尽量少,则其表面积就会小.
8.C
【分析】图A横排的四个正方形能折成正方体的四个面,另外两个正方形在这四个正方形的两旁,能折成正方体的另外两个面,能折成正方体;图B纵排的四个正方形能折成正方体的四个面,另外两个正方形在这四个正方形的两旁,能折成正方体的另外两个面,能折成正方体;图C上面的一个正方形能折成正方体的一个面,横排着五个正方形,折成正方体的四个面只需要四个正方形,剩下的一个正方形不能折成正方体的一个面,不能折成正方体。
【详解】由分析可知:图A和图B能折成正方体;图C不能折成正方体;
故选:C
【点睛】本题主要是考查正方体的展开图,训练学生的空间想象能力。
9. 展开 折叠
【解析】略
10.320
【分析】把这2个这样的长方体纸盒包成一包,要想使表面积最小,那么应该把它们的最大的面相粘合,由此拼成的新长方体的长、宽、高分别是:8cm、6cm、(4+4)cm,根据长方体的表面积公式:S=(ab+ah+bh)×2,把数据代入公式解答。
【详解】4+4=8(cm)
(8×6+8×8+8×6)×2
=(48+64+48)×2
=(112+48)×2
=160×2
=320(cm2)
【点睛】此题主要考查长方体的表面积公式的灵活运用。解答关键是理解:把它们的最大的面相粘合,包装最省纸。
11. 24 20 8
【分析】根据题目中的调查情况,可以分别计算出喜欢唱《春晓》、《静夜思》、《悯农》的人数,然后即可将表格补充完整。
【详解】6+6+6+6
=12+6+6
=18+6
=24(人)
7+7+6
=14+6
=20(人)
6+6-4
=12-4
=8(人)
名称 《春晓》 《静夜思》 《悯农》
人数 24 20 8
【点睛】本题考查统计图表的填补,明确题意,从统计图表中获取解答问题的信息是解答本题的关键。
12.小房子
【详解】本题属于操作题,通过操作可以想像折成的立体图形像什么。观察上图,房顶的侧面是边长分别为2cm、2cm、3cm的三角形,房子的侧面是长4cm、宽3cm的长方形,这两个长方形夹着的长8cm、宽4cm的大长方形就是小房子的正面;将上面展开图按虚线折叠成一个封闭的立体图形,它的形状像小房子。
13.(1)踢球;跳远
(2)4
(3)参加跳绳的人数是参加跳远的人数的3倍
(4)12;18;4;10
【分析】(1)从统计图可知,参加踢球的人数最多,参加跳远的人数最少。
(2)从统计图可知,参加跳绳的同学比参加跳远的多4人。
(3)从统计图可知,参加跳绳的人数是参加跳远的人数的3倍。
(4)根据每个表示2个同学,利用乘法的意义解答即可。
【详解】(1)参加踢球的人数最多,参加跳远的人数最少。
(2)参加跳绳的同学比参加跳远的多4人。
(3)从统计图可知,参加跳绳的人数是参加跳远的人数的3倍。
(4)
活动 跳绳 踢球 跳远 踢毽子
人数 12 18 4 10
【点睛】本题考查了条形统计图的画法以及从统计图表中获取信息的能力。
14. 7 8 15 11 5 《昆虫记》 《成语故事》 4 46
【分析】(1)根据同学最喜欢的图书“正”字,填入统计表相应的格内;
(2)分别比较同学最喜欢的图书情况,即可得最喜欢《昆虫记》的人数最多,最喜欢《成语故事》的人数最少;
(3)最喜欢《昆虫记》的有15人,最喜欢《父与子》的有11人,用15-11=4,即可得最喜欢《昆虫记》的比最喜欢《父与子》的多几人;
(4)根据加法的意义,把喜欢各类图书的人数加起来即可得这个班一共多少人。
【详解】(1)把上面的统计结果填在如表中。
图书名称 《二年级的小豆豆》 《格林童话》 《昆虫记》 《父与子》 《成语故事》
人数 7 8 15 11 5
(2)最喜欢《二年级的小豆豆》的有7人,
最喜欢《格林童话》的有8人,
最喜欢《昆虫记》的有15人,
最喜欢《父与子》的有11人,
最喜欢《成语故事》的有5人,
通过比较可知:最喜欢《昆虫记》的人数最多,最喜欢《成语故事》的人数最少;
(3)最喜欢《昆虫记》的有15人,最喜欢《父与子》的有11人,
15-11=4(人)
(4)7+8+15+11+5=46(人)
【点睛】此题考查的目的是理解掌握统计表的特点及作用,并且能够根据统计表提供的信息,解决有关的实际问题。
15.128
【分析】
当正方体被分成两个完全相同的长方体后,表面积增加了2个正方体的底面积,也就是2个边长为8cm的正方形的面积和。
【详解】8×8×2
=64×2
=128(cm2)
表面积增加了128cm2。
16.错误
【分析】先把方程1+2x=15,依据等式的性质求出x的值,再把x的值代入13x﹣7x,看求出的值是否等于30解答。
【详解】1+2x=15,
1+2x﹣1=15﹣1,
2x÷2=14÷2,
x=7;
把x=7代入:
13x﹣7x,
=13×7﹣7×7,
=91﹣49,
=42,
42≠30,
故答案为错误。
【点睛】本题主要考查学生依据等式的性质解方程的能力。
17.√
【分析】根据正方形的周长求出正方形的边长,再看长方形纸的长和宽是否大于正方形的边长即可。
【详解】正方形的周长是16厘米,则边长是16÷4=4(厘米)。因为长方形纸的长是7厘米、宽是4厘米,均大于4厘米,所以可以折成。
故答案为:√
【点睛】本题主要考查的是正方形和长方形特征以及周长公式的应用。
18.×
【分析】根据正方体展开图的特征,图1、图2都不能折成一个无盖的正方体,只有图3比正方体展开图的“3-3”型少一个正方形,正好折成一个无盖的正方体。
【详解】观察三个展开图,再结合正方体展开图的特征可知:
图1和图2均不能折成一个无盖的正方体,但图3能折成一个无盖的正方体。
故答案为:×。
【点睛】正方体展开图有11种特征,分四种类型,即:第一种:“1-4-1”结构,即第一行放1个,第二行放4个,第三行放1个;第二种:“2-2-2”结构,即每一行放2个正方形,此种结构只有一种展开图;第三种:“3-3”结构,即每一行放3个正方形,只有一种展开图;第四种:“1-3-2”结构,即第一行放1个正方形,第二行放3个正方形,第三行放2个正方形。无盖的正方体在四种类型上变化即可。
19.错误
【详解】略
20.5千米
【分析】先利用6乘1.5小时,求出从山脚到山顶的路程。再将其除以1.8小时,求出他们实际每小时走多少千米。
【详解】6×1.5÷1.8
=9÷1.8
=5(千米)
答:他们平均每小时走5千米。
【点睛】本题考查了行程问题,灵活运用“速度×时间=路程”是解题的关键。
21.48米
【分析】把小军的速度设为未知数,等量关系式:(小娟的速度+小军的速度)×行驶时间=小娟家和小军家的距离,据此解答。
【详解】解:设小军平均每分钟走x米。
(42+x)×8=720
42+x=720÷8
42+x=90
x=90-42
x=48
答:小军平均每分钟走48米。
【点睛】掌握路程、时间、速度之间的数量关系是解答题目的关键。
22.0.25小时
【分析】根据通车前的速度和时间,可求出总路程,再根据“时间=路程÷速度”求出通车后的时间即可。
【详解】40×0.5÷80
=20÷80
=0.25(小时)
答:需要0.25小时。
【点睛】根据通车前的速度和时间,求出总路程是解答本题的关键。
23.90千米
【分析】先根据剩余的路程=总路程-已行驶路程,求出客车前1.5小时行驶路程,再根据速度=路程÷时间,求出最后的速度,列式解答即可。
【详解】(195-1.5×82)÷0.8
=72÷0.8
=90(千米)
【点睛】解答本题的依据是等量关系式:速度=路程÷时间,关键是求出客车前1.5小时行驶路程,和后剩余的路程。
24.(1)72厘米
(2)312平方厘米
【分析】(1)从图中可知,扎这个礼品盒用去丝带的长度=两条长+两条宽+4条高+打结处丝带的长度。
(2)求制作这样一个礼品盒,至少需要纸板的面积,就是求长方体的表面积,根据长方体的表面积=(长×宽+长×高+宽×高)×2,代入数据计算即可。
【详解】(1)12×2+8×2+3×4+20
=24+16+12+20
=72(厘米)
答:扎这个礼品盒用去丝带72厘米。
(2)(12×8+12×3+8×3)×2
=(96+36+24)×2
=156×2
=312(平方厘米)
答:至少需要纸板312平方厘米。
【点睛】本题考查长方体棱长总和、表面积公式的灵活运用,关键是结合图形,分析出给礼品盒扎丝带时的包装方法。
答案第1页,共2页
答案第1页,共2页
(共24题,满分100分)
题号 一 二 三 四 总分
得分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.注意书写整洁
一、选择题
1.下面的展开图折叠后所围成的图形是( )。
A. B. C.
2.两盒糖果包成一包,( )种包装方法最节省包装纸。
A. B. C.
3.把4个长8厘米,宽6厘米,高4厘米的长方体盒子(如图),包装成一个大长方体礼盒,下面最节约包装纸的是( )。
A. B. C.
4.下面的平面图形中,不能围成长方体或正方体的是( )。
A. B. C.
5.一种长方体礼品盒如图所示,现将两个这样的礼品盒包装在一起,最省包装纸的方法是( )。
A.方法一 B.方法二 C.方法三
6.用做成一个,数字“2”的对面是数字( )。
A.4 B.5 C.6
7.有2盒磁带,用下面的三种方法包装,( )种包装纸最省.
A. B. C.
8.下面3个平面图形中(每个格是正方形),不能折成是正方体的是( )。
A. B. C.
二、填空题
9.有些立体图形通过( )就可以变成平面图形。有些平面图形通过( )就可以变成立体图形。
10.一个长方体纸盒,长8cm、宽6cm、高4cm。如果把2个这样的长方体纸盒包成一大包,至少需要包装纸( )cm2。
11.《经典咏流传》比赛前,豆豆做了一个最喜欢唱的古诗的调查。
喜欢唱《春晓》的人数:4个6相加的和。
喜欢唱《静夜思》的人数:比2个7相加的和多6。
喜欢唱《悯农》的人数:比2个6相加的和少4。
根据上面的信息,完成如表。
名称 《春晓》 《静夜思》 《悯农》
人数 ( ) ( ) ( )
12.将下图按虚线折叠成一个封闭的立体图形,它的形状像什么?
分析与解答:它的形状像( )。
观察上图,房顶的侧面是边长分别为2cm、2cm、3cm的三角形,房子的侧面是长4cm、宽3cm的长方形,这两个长方形夹着的长8cm、宽4cm的大长方形就是小房子的正面。
13.下面是二(1)班同学体育课上参加体育活动的情况。
(1)参加( )的人数最多,参加( )的人数最少。
(2)参加跳绳的同学比参加跳远的多( )人。
(3)你还发现了什么?
(4)如果每个表示2个同学,上面的数据应该是多少?填一填。
活动 跳绳 踢球 跳远 踢毽子
人数 ( ) ( ) ( ) ( )
14.下面是二(3)班同学最喜欢的图书情况。
图书名称 《二年级的小豆豆》 《格林童话》 《昆虫记》 《父与子》 《成语故事》
人数 正 正 正正正 正正一 正
(1)把上面的统计结果填在如表中。
图书名称 《二年级的小豆豆》 《格林童话》 《昆虫记》 《父与子》 《成语故事》
人数
(2)最喜欢( )的人数最多,最喜欢( )的人数最少。
(3)最喜欢《昆虫记》的比最喜欢《父与子》的多( )人。
(4)这个班一共( )人。
15.将一个棱长为8cm的正方体分成两个相同的长方体,表面积增加了( )cm2。
三、判断题
16.如果1+2x=15,那么13x﹣7x=30。( )
17.用长7厘米、宽4厘米的长方形纸能折出一个周长是16厘米的正方形。( )
18.、、都不能折成一个无盖的正方体。( )
19.七巧板中没有平行四边形这个图形.( )
四、解决问题
20.小明和芳芳去爬山。
21.小娟和小军在校门口分手。8分钟后他们同时到家,小娟平均每分钟走42m,小军平均每分钟走多少米?
22.李阿姨带着陈阿姨去体验洛阳王城大道快速路。洛阳王城大道快速路通车前小汽车从龙门高铁站到北郊机场走王城大道需要0.5小时,每小时行40千米。通车后(公路全长不变),她俩乘小汽车从龙门高铁站到北郊机场走王城大道快速路,每小时行80千米,需要多少小时?
23.一辆客车从甲城开往乙城两城相距195千米。在前1.5小时的时间里平均每小时行82千米,剩下的路程0.8小时行完。平均每小时需行多少千米?
24.在5月的第二个星期日是母亲节。母亲节这天,张亮为妈妈买了礼物,他按下面的方法给礼品盒扎丝带,打结处用去丝带20厘米。
(1)扎这个礼品盒用去丝带多少厘米?
(2)制作这样一个礼品盒,至少需要纸板多少平方厘米?(接缝处忽略不计)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
) (
学校:___________姓名:___________班级:___________考号:___________
) (
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
第1页 共4页 ◎ 第2页 共4页
第1页 共4页 ◎ 第2页 共4页
参考答案:
1.A
【分析】根据展开图可知,围成的图形的上下面是两个相同的三角形,侧面是由3个长方形组成,也就是一个三棱柱,据此选择。
【详解】由分析可知,展开图折叠后所围成的图形是。
故选择:A
【点睛】此题考查了图形的展开与折叠,培养了学生的空间想象能力。
2.C
【分析】首先搞清是求长方体的表面积.要求怎样包装才能节约包装纸,应使这两盒糖果接触的面积最大,也就是说让最大面结合在一起,据此解答即可。
【详解】由分析可知:
将两盒糖包装成一包,最省包装纸的方案是C。
故答案为:C
【点睛】这是一道长方体表面积的实际应用,考查了学生对长方体表面积计算公式的掌握情况,以及实际操作能力。
3.B
【分析】求出选项中各长方体的长、宽、高,利用“长方体的表面积=(长×宽+宽×高+长×高)×2”求出长方体的表面积,最后比较大小,据此解答。
【详解】A.长:8×2=16(厘米)
宽:6×2=12(厘米)
高:4厘米
(16×12+16×4+12×4)×2
=(192+64+48)×2
=304×2
=608(平方厘米)
B.长:8厘米
宽:6×2=12(厘米)
高:4×2=8(厘米)
(8×12+8×8+12×8)×2
=(96+64+96)×2
=256×2
=512(平方厘米)
C.长:8厘米
宽:6厘米
高:4×4=16(厘米)
(8×6+8×16+6×16)×2
=(48+128+96)×2
=272×2
=544(平方厘米)
因为512平方厘米<544平方厘米<608平方厘米,所以最节约包装纸的是。
故答案为:B
【点睛】本题主要考查了包装问题,掌握长方体的表面积计算公式是解答题目的关键。
4.B
【分析】通过空间想象,一一分析,找出不能围成长方体或正方体的平面图形。
【详解】A.能围成一个长方体;
B.不能围成长方体或正方体;
C.能围成一个正方体。
故答案为:B
【点睛】本题考查了长方体或正方体的展开图,有一定空间想象力是解题的关键。
5.C
【分析】将两个礼品盒包装在一起,最省包装纸的方法是:把长方体中最大的面覆盖起来。这样包装在一起后表面积最小,即最省包装纸。
【详解】观察长方体礼品盒,结合长方体礼品盒长宽高数据可知,长方体的上、下面面积最大,则方法三最省包装纸。
故答案为:C
【点睛】求几个盒子包装在一起最省包装纸的方法,使包装好的图形表面积最小即可。
6.A
【分析】根据正方体展开图的11种特征,左面的平面图属于正方体展开图的“1-4-1”型,折成正方体后,数字“1”与“3”相对,“2”与“4”相对,“5”与“6”相对。
【详解】用做成一个,数字“2”的对面是数字“4”。
故答案为:A。
【点睛】正方体展开图分四种类型,11种情况,每种情况折成正方体后哪些面相对是有规律的,可自己动手操作一下并记住,能快速解答此类题。
7.A
【详解】试题分析:要想更省包装纸,需使表面积最小,由题意可知:只要让磁带的最大面露出的尽量少,则其表面积就会小,也就更能省包装纸,据此即可作出正确选择.
解:由图意可知:选项A露出的最大面最少,则其表面积最小,
所以A最省包装纸;
故选A.
点评:解答此题的关键是明白:要想更省包装纸,需使表面积最小,本题中,只要让磁带的最大面露出的尽量少,则其表面积就会小.
8.C
【分析】图A横排的四个正方形能折成正方体的四个面,另外两个正方形在这四个正方形的两旁,能折成正方体的另外两个面,能折成正方体;图B纵排的四个正方形能折成正方体的四个面,另外两个正方形在这四个正方形的两旁,能折成正方体的另外两个面,能折成正方体;图C上面的一个正方形能折成正方体的一个面,横排着五个正方形,折成正方体的四个面只需要四个正方形,剩下的一个正方形不能折成正方体的一个面,不能折成正方体。
【详解】由分析可知:图A和图B能折成正方体;图C不能折成正方体;
故选:C
【点睛】本题主要是考查正方体的展开图,训练学生的空间想象能力。
9. 展开 折叠
【解析】略
10.320
【分析】把这2个这样的长方体纸盒包成一包,要想使表面积最小,那么应该把它们的最大的面相粘合,由此拼成的新长方体的长、宽、高分别是:8cm、6cm、(4+4)cm,根据长方体的表面积公式:S=(ab+ah+bh)×2,把数据代入公式解答。
【详解】4+4=8(cm)
(8×6+8×8+8×6)×2
=(48+64+48)×2
=(112+48)×2
=160×2
=320(cm2)
【点睛】此题主要考查长方体的表面积公式的灵活运用。解答关键是理解:把它们的最大的面相粘合,包装最省纸。
11. 24 20 8
【分析】根据题目中的调查情况,可以分别计算出喜欢唱《春晓》、《静夜思》、《悯农》的人数,然后即可将表格补充完整。
【详解】6+6+6+6
=12+6+6
=18+6
=24(人)
7+7+6
=14+6
=20(人)
6+6-4
=12-4
=8(人)
名称 《春晓》 《静夜思》 《悯农》
人数 24 20 8
【点睛】本题考查统计图表的填补,明确题意,从统计图表中获取解答问题的信息是解答本题的关键。
12.小房子
【详解】本题属于操作题,通过操作可以想像折成的立体图形像什么。观察上图,房顶的侧面是边长分别为2cm、2cm、3cm的三角形,房子的侧面是长4cm、宽3cm的长方形,这两个长方形夹着的长8cm、宽4cm的大长方形就是小房子的正面;将上面展开图按虚线折叠成一个封闭的立体图形,它的形状像小房子。
13.(1)踢球;跳远
(2)4
(3)参加跳绳的人数是参加跳远的人数的3倍
(4)12;18;4;10
【分析】(1)从统计图可知,参加踢球的人数最多,参加跳远的人数最少。
(2)从统计图可知,参加跳绳的同学比参加跳远的多4人。
(3)从统计图可知,参加跳绳的人数是参加跳远的人数的3倍。
(4)根据每个表示2个同学,利用乘法的意义解答即可。
【详解】(1)参加踢球的人数最多,参加跳远的人数最少。
(2)参加跳绳的同学比参加跳远的多4人。
(3)从统计图可知,参加跳绳的人数是参加跳远的人数的3倍。
(4)
活动 跳绳 踢球 跳远 踢毽子
人数 12 18 4 10
【点睛】本题考查了条形统计图的画法以及从统计图表中获取信息的能力。
14. 7 8 15 11 5 《昆虫记》 《成语故事》 4 46
【分析】(1)根据同学最喜欢的图书“正”字,填入统计表相应的格内;
(2)分别比较同学最喜欢的图书情况,即可得最喜欢《昆虫记》的人数最多,最喜欢《成语故事》的人数最少;
(3)最喜欢《昆虫记》的有15人,最喜欢《父与子》的有11人,用15-11=4,即可得最喜欢《昆虫记》的比最喜欢《父与子》的多几人;
(4)根据加法的意义,把喜欢各类图书的人数加起来即可得这个班一共多少人。
【详解】(1)把上面的统计结果填在如表中。
图书名称 《二年级的小豆豆》 《格林童话》 《昆虫记》 《父与子》 《成语故事》
人数 7 8 15 11 5
(2)最喜欢《二年级的小豆豆》的有7人,
最喜欢《格林童话》的有8人,
最喜欢《昆虫记》的有15人,
最喜欢《父与子》的有11人,
最喜欢《成语故事》的有5人,
通过比较可知:最喜欢《昆虫记》的人数最多,最喜欢《成语故事》的人数最少;
(3)最喜欢《昆虫记》的有15人,最喜欢《父与子》的有11人,
15-11=4(人)
(4)7+8+15+11+5=46(人)
【点睛】此题考查的目的是理解掌握统计表的特点及作用,并且能够根据统计表提供的信息,解决有关的实际问题。
15.128
【分析】
当正方体被分成两个完全相同的长方体后,表面积增加了2个正方体的底面积,也就是2个边长为8cm的正方形的面积和。
【详解】8×8×2
=64×2
=128(cm2)
表面积增加了128cm2。
16.错误
【分析】先把方程1+2x=15,依据等式的性质求出x的值,再把x的值代入13x﹣7x,看求出的值是否等于30解答。
【详解】1+2x=15,
1+2x﹣1=15﹣1,
2x÷2=14÷2,
x=7;
把x=7代入:
13x﹣7x,
=13×7﹣7×7,
=91﹣49,
=42,
42≠30,
故答案为错误。
【点睛】本题主要考查学生依据等式的性质解方程的能力。
17.√
【分析】根据正方形的周长求出正方形的边长,再看长方形纸的长和宽是否大于正方形的边长即可。
【详解】正方形的周长是16厘米,则边长是16÷4=4(厘米)。因为长方形纸的长是7厘米、宽是4厘米,均大于4厘米,所以可以折成。
故答案为:√
【点睛】本题主要考查的是正方形和长方形特征以及周长公式的应用。
18.×
【分析】根据正方体展开图的特征,图1、图2都不能折成一个无盖的正方体,只有图3比正方体展开图的“3-3”型少一个正方形,正好折成一个无盖的正方体。
【详解】观察三个展开图,再结合正方体展开图的特征可知:
图1和图2均不能折成一个无盖的正方体,但图3能折成一个无盖的正方体。
故答案为:×。
【点睛】正方体展开图有11种特征,分四种类型,即:第一种:“1-4-1”结构,即第一行放1个,第二行放4个,第三行放1个;第二种:“2-2-2”结构,即每一行放2个正方形,此种结构只有一种展开图;第三种:“3-3”结构,即每一行放3个正方形,只有一种展开图;第四种:“1-3-2”结构,即第一行放1个正方形,第二行放3个正方形,第三行放2个正方形。无盖的正方体在四种类型上变化即可。
19.错误
【详解】略
20.5千米
【分析】先利用6乘1.5小时,求出从山脚到山顶的路程。再将其除以1.8小时,求出他们实际每小时走多少千米。
【详解】6×1.5÷1.8
=9÷1.8
=5(千米)
答:他们平均每小时走5千米。
【点睛】本题考查了行程问题,灵活运用“速度×时间=路程”是解题的关键。
21.48米
【分析】把小军的速度设为未知数,等量关系式:(小娟的速度+小军的速度)×行驶时间=小娟家和小军家的距离,据此解答。
【详解】解:设小军平均每分钟走x米。
(42+x)×8=720
42+x=720÷8
42+x=90
x=90-42
x=48
答:小军平均每分钟走48米。
【点睛】掌握路程、时间、速度之间的数量关系是解答题目的关键。
22.0.25小时
【分析】根据通车前的速度和时间,可求出总路程,再根据“时间=路程÷速度”求出通车后的时间即可。
【详解】40×0.5÷80
=20÷80
=0.25(小时)
答:需要0.25小时。
【点睛】根据通车前的速度和时间,求出总路程是解答本题的关键。
23.90千米
【分析】先根据剩余的路程=总路程-已行驶路程,求出客车前1.5小时行驶路程,再根据速度=路程÷时间,求出最后的速度,列式解答即可。
【详解】(195-1.5×82)÷0.8
=72÷0.8
=90(千米)
【点睛】解答本题的依据是等量关系式:速度=路程÷时间,关键是求出客车前1.5小时行驶路程,和后剩余的路程。
24.(1)72厘米
(2)312平方厘米
【分析】(1)从图中可知,扎这个礼品盒用去丝带的长度=两条长+两条宽+4条高+打结处丝带的长度。
(2)求制作这样一个礼品盒,至少需要纸板的面积,就是求长方体的表面积,根据长方体的表面积=(长×宽+长×高+宽×高)×2,代入数据计算即可。
【详解】(1)12×2+8×2+3×4+20
=24+16+12+20
=72(厘米)
答:扎这个礼品盒用去丝带72厘米。
(2)(12×8+12×3+8×3)×2
=(96+36+24)×2
=156×2
=312(平方厘米)
答:至少需要纸板312平方厘米。
【点睛】本题考查长方体棱长总和、表面积公式的灵活运用,关键是结合图形,分析出给礼品盒扎丝带时的包装方法。
答案第1页,共2页
答案第1页,共2页
