4.3长方体的体积同步练习 北师大版数学五年级下册(含解析)
文档属性
| 名称 | 4.3长方体的体积同步练习 北师大版数学五年级下册(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 102.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-03 00:00:00 | ||
图片预览





文档简介
4.3长方体的体积
(共26题,满分100分)
题号 一 二 三 四 总分
得分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.注意书写整洁
一、选择题
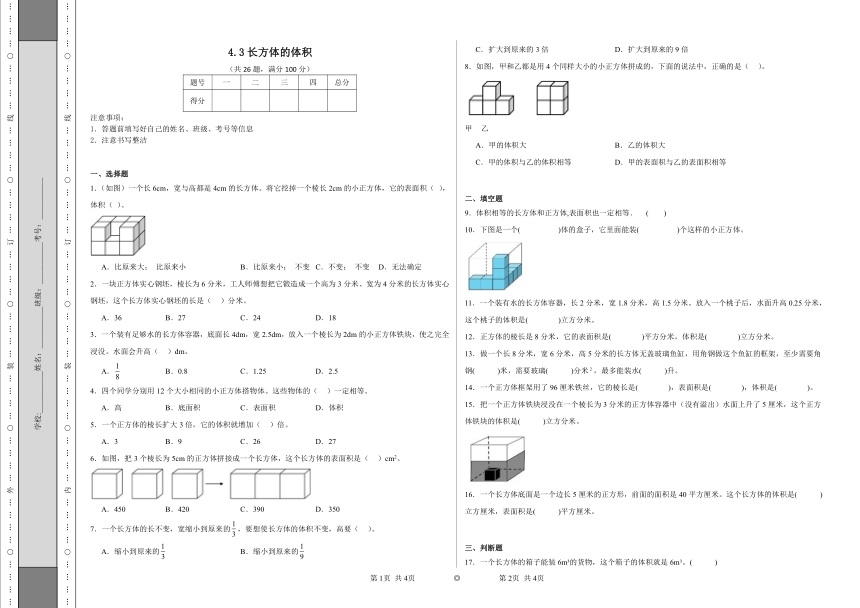
1.(如图)一个长6cm,宽与高都是4cm的长方体。将它挖掉一个棱长2cm的小正方体,它的表面积( ),体积( )。
A.比原来大; 比原来小 B.比原来小; 不变 C.不变; 不变 D.无法确定
2.一块正方体实心钢坯,棱长为6分米,工人师傅想把它锻造成一个高为3分米、宽为4分米的长方体实心钢坯,这个长方体实心钢坯的长是( )分米。
A.36 B.27 C.24 D.18
3.一个装有足够水的长方体容器,底面长4dm,宽2.5dm,放入一个棱长为2dm的小正方体铁块,使之完全浸没。水面会升高( )dm。
A. B.0.8 C.1.25 D.2.5
4.四个同学分别用12个大小相同的小正方体搭物体。这些物体的( )一定相等。
A.高 B.底面积 C.表面积 D.体积
5.一个正方体的棱长扩大3倍,它的体积就增加( )倍。
A.3 B.9 C.26 D.27
6.如图,把3个棱长为5cm的正方体拼接成一个长方体,这个长方体的表面积是( )cm2。
A.450 B.420 C.390 D.350
7.一个长方体的长不变,宽缩小到原来的,要想使长方体的体积不变,高要( )。
A.缩小到原来的 B.缩小到原来的
C.扩大到原来的3倍 D.扩大到原来的9倍
8.如图,甲和乙都是用4个同样大小的小正方体拼成的,下面的说法中,正确的是( )。
甲 乙
A.甲的体积大 B.乙的体积大
C.甲的体积与乙的体积相等 D.甲的表面积与乙的表面积相等
二、填空题
9.体积相等的长方体和正方体,表面积也一定相等. ( )
10.下图是一个( )体的盒子,它里面能装( )个这样的小正方体。
11.一个装有水的长方体容器,长2分米,宽1.8分米,高1.5分米。放入一个桃子后,水面升高0.25分米,这个桃子的体积是( )立方分米。
12.正方体的棱长是8分米,它的表面积是( )平方分米,体积是( )立方分米。
13.做一个长8分米,宽6分米,高5分米的长方体无盖玻璃鱼缸,用角钢做这个鱼缸的框架,至少需要角钢( )米,需要玻璃( )分米,最多能装水( )升。
14.一个正方体框架用了96厘米铁丝,它的棱长是( ),表面积是( ),体积是( )。
15.把一个正方体铁块浸没在一个棱长为3分米的正方体容器中(没有溢出)水面上升了5厘米,这个正方体铁块的体积是( )立方分米。
16.一个长方体底面是一个边长5厘米的正方形,前面的面积是40平方厘米。这个长方体的体积是( )立方厘米,表面积是( )平方厘米。
三、判断题
17.一个长方体的箱子能装6m 的货物,这个箱子的体积就是6m 。( )
18.正方体的棱长扩大2倍,则表面积和体积都扩大4倍。( )
19.棱长和相等的正方体与长方体的表面积不相等,但它们的体积相等。( )
20.棱长1分米的正方体最多可以截成5个棱长2厘米的小正方体。( )
21.是由体积是1立方厘米的小正方体组成的,它的体积是4立方厘米。( )
四、解答题
22.幼儿园有一排长方体储物柜,共占地0.84m ,储物柜的高均为75cm,这排储物柜所占的空间是多少立方米?
23.一块体积为0.48立方米的长方体钢材,底面是边长为0.2米的正方形,这块钢材有多长?
24.有一个长方体,表面积是184平方厘米,底面积是20平方厘米,底面周长是18厘米,这个长方体的体积是多少立方厘米?
25.在一块长90米,宽56米的长方形地上铺一层厚4厘米的沙土.
(1)需要多少沙土?
(2)一辆车每次运送1.5米3的沙土,至少需要运多少次?
26.在一个长为10米、宽为3.5米的长方形客厅的地面上铺设2厘米厚的木地板,至少需要木材多少立方米?铺好后要在地板上涂油漆,涂油漆部分的面积是多少?
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
) (
学校:___________姓名:___________班级:___________考号:___________
) (
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
第1页 共4页 ◎ 第2页 共4页
第1页 共4页 ◎ 第2页 共4页
参考答案:
1.A
【分析】由图意知:从长方体中挖掉一个棱长2cm的小正方体,少了小正方体的正面和上面,但又多了下面小正方体的上面和里面小正方体的正面、左右两个小正方体的左右侧面,也就是减少两个面,多了四个面,表面积变大;因少了一个小正方体,体积减少。据此解答。
【详解】由分析知:这个长方体的表面积多了两个小正方体的面,表面积增大,体积变小。
故答案为:A
【点睛】本题考查了长方体的表面积和体积、了解如上图挖掉一个小正方体,表面积增加了两个小正方体的面,体积变小是解答本题的关键。
2.D
【分析】把正方体实心钢坯锻造成长方体,体积不变;根据正方体体积公式:体积=棱长×棱长×棱长,代入数据,求出正方体实心钢胚的体积,再根据长方体体积公式:体积=长×宽×高;长=体积÷(宽×高),代入数据,即可解答。
【详解】6×6×6÷(4×3)
=36×6÷12
=216÷12
=18(分米)
一块正方体实心钢坯,棱长为6分米,工人师傅想把它锻造成一个高为3分米、宽为4分米的长方体实心钢坯,这个长方体实心钢坯的长是18分米。
故答案为:D
【点睛】熟练掌握和灵活运用长方体体积公式和正方体体积公式是解答本题的关键。
3.B
【分析】长方体容器中原来装有足够的水,而铁块本身具有一定的体积,放入水中后会占有一定的空间,导致水面上升,此时,水面升高所增加的水的体积就等于铁块的体积,则水面上升的高度=水面上升的体积÷长方体容器的底面积。
【详解】-
=8÷10
=0.8(dm)
故答案为:B
【点睛】解决这类问题,要特别注意两点:一是放入物体后水面是否溢出,二是物体是否完全浸入水中。
4.D
【分析】用12个大小相同的小正方体搭物体,无论搭成什么形状,体积都等于12个小正方体的体积之和,但是底面积、高和表面积都有可能发生变化,据此选择。
【详解】由分析可知,四个同学分别用12个大小相同的小正方体搭物体。这些物体的体积一定相等。
故选择:D
【点睛】此题考查了立体图形的切拼,明确物体的体积不会随着物体的形状发生变化。
5.C
【分析】根据正方体的体积公式:,再根据因数与积的变化规律,正方体的棱长扩大3倍,体积扩大27倍,所以它的体积增加(27-1)倍,据此解答。
【详解】一个正方体的棱长扩大3倍,它的体积就扩大倍
它的体积就增加
故答案为:C
【点睛】此题考查的目的是理解掌握正方体的体积公式。
6.D
【分析】3个正方体拼接一个长方体,长方体的长=正方体的棱长×3,长方体的宽=正方体的棱长,长方体的高=正方体的棱长,根据长方体的表面积公式:表面积=(长×宽+长×高+宽×高)×2,代入数据,即可解答。
【详解】长方体的长:5×3=15(cm),宽:5cm,高:5cm。
(15×5+15×5+5×5)×2
=(75+75+25)×2
=(150+25)×2
=175×2
=350(cm2)
故答案为:D
【点睛】本题考查立体图形的切拼,以及长方体表面积公式的应用,熟练掌握长方体表面积公式,是解答本题的关键。
7.C
【分析】根据长方体的体积=长×宽×高,依据积不变的规律可知,其中一个乘数缩小到原来的,如果要使积不变,那么另一个乘数扩大到原来的3倍。
【详解】根据分析可知,一个长方体的长不变,宽缩小到原来的,要想使长方体的体积不变,高要扩大到原来的3倍。
故答案为:C
【点睛】此题主要考查学生对长方体体积的认识与了解,也考查了积不变的规律。
8.C
【分析】由图可知:甲比原来4个小正方体减少6个正方形面,体积等于4个小正方体体积之和;乙比原来4个小正方体减少8个正方形面,体积等于4个小正方体体积之和;据此解答。
【详解】因为甲比原来4个小正方体减少6个正方形面;乙比原来4个小正方体减少8个正方形面,乙减少的多,所以甲的表面积大于乙的表面积;
甲的体积=等于4个小正方体体积之和=乙的体积,所以甲的体积与乙的体积相等。
故答案为:C
【点睛】本题主要考查立体图形的切拼,解题时要明确拼接时体积就不变。
9.×
【分析】长方体的体积=长×宽×高,正方体的体积=棱长×棱长×棱长,此题可以采用举例说明的方法进行判断.
【详解】一个长方体和正方体的体积相等,都是8,
所以正方体的棱长是2,表面积是2×2×6=24;
长方体的长宽高可以分别是:1、2、4,表面积是1×2×2+1×4×2+2×4×2,
=4+8+16,
=28,
所以原题说法错误.
故答案为×.
10. 长方 36
【分析】观察图可知,它是一个长方体的盒子,长方体的长是3,宽是4,高是3,即长方体的盒子里一行能摆3个小正方体,能摆4行,总共有3层。根据长方体的体积计算公式V=abh计算出能装多少个小正方体。
【详解】它是一个长方体的盒子
3×4×3
=12×3
=36(个)
【点睛】本题考查的是长方体体积计算公式的运用,熟练掌握它的体积并灵活运用。
11.0.9
【分析】根据题意可知,把桃子放入容器中,上升部分水的体积就等于桃子的体积,根据长方体的体积公式:V=abh,把数据代入公式解答。
【详解】2×1.8×0.25
=3.6×0.25
=0.9(立方分米)
【点睛】此题主要考查长方体的体积(容积)公式的灵活运用,关键是熟记公式。
12. 384 512
【分析】根据正方体的表面积公式:S=6a2,体积公式:V=a3,把数据分别代入公式解答。
【详解】8×8×6
=64×6
=384(平方分米);
8×8×8
=64×8
=512(立方分米);
【点睛】此题主要考查正方体的表面积公式、体积公式的灵活运用,关键是熟记公式。
13. 7.6 188 240
【分析】至少需要多少角钢,就是求长方体的棱长之和;
做这个鱼缸至少需要玻璃多少平方分米,就是求长方体5个面的面积;
鱼缸最多可以装水多少升,就是求长方体的体积,长方体的体积=长×宽×高。
【详解】(8+6+5)×4
=19×4
=76(分米)
=7.6(米)
8×6+(8×5+5×6)×2
=48+140
=188(分米)
8×6×5
=48×5
=240(分米3)
=240(升)
【点睛】考查了长方体的棱长、表面积、体积的实际应用,学生应掌握。
14. 8厘米 384平方厘米 512立方厘米
【分析】根据正方体的棱长总和=棱长×12,那么棱长=棱长总和÷12,据此求出棱长,再根据正方体的表面积公式:S=6a2,正方体的体积公式:V=a3,把数据代入公式解答。
【详解】96÷12=8(厘米)
8×8×6
=64×6
=384(平方厘米)
8×8×8
=64×8
=512(立方厘米)
【点睛】此题主要看正方体的棱长总和公式、表面积公式、体积公式的灵活运用,关键是熟记公式。
15.4.5
【分析】根据题意可知:容器中上升部分水的体积等于这个正方体铁块的体积,根据长方体的体积=底面积×高,求出这个正方体铁块的体积。
【详解】5厘米=0.5分米
3×3×0.5
=9×0.5
=4.5(立方分米)
【点睛】此题主要考查长方体的体积公式的灵活运用,关键是熟记公式。
16. 200 210
【分析】前面的面积=长×高,由此可以求出高,再根据长方体的体积公式、表面积公式解答即可。
【详解】40÷5=8(厘米)
5×5×8
=25×8
=200(立方厘米)
5×5×2+5×8×4
=50+160
=210(平方厘米)
【点睛】此题主要考查长方体的体积公式、表面积公式的灵活运用,关键是熟记公式。
17.×
【分析】物体的体积是指物体所占空间的大小,物体的容积是指物体所能容纳物体的大小,求物体的体积从物体外面测量有关数据,而容积是从里面测量有关数据。
【详解】根据分析可知,一个长方体的箱子能装6m 的货物,这个箱子的容积就是6m ,体积要大于容积。
故答案为:×
【点睛】本题是考查体积和容积的意义,注意,体积和容积是两个不同的概念,有计时容器的壁较薄可能忽略不计,但不是说物体的体积就是容积。
18.×
【分析】根据正方体的表面积公式:S=6a2,再根据因数与积的变化规律,积扩大的倍数等于因数扩大倍数的乘积,据此判断即可。
【详解】正方体的棱长扩大2倍,它的表面积就扩大倍。
体积扩大倍。
因此,正方体的棱长扩大2倍,则表面积和体积都扩大4倍。这种说法是错误的。
故答案为:×
【点睛】此题考查的目的是理解掌握正方体的表面积公式、因数与积的变化规律及应用。
19.×
【详解】略
20.×
【分析】把1分米化成10厘米,10÷2=5,大正方体的每条棱上都可截得5个棱长为2厘米的小正方体,所以一共可以截得5×5×5=125个小正方体。据此判断。
【详解】根据分析可得:
1分米=10厘米
10÷2=5(个)
所以5×5×5=125(个)
故答案为:×
【点睛】本题也可以利用大正方体的体积除以小正方体的体积求出切割出的小正方体的总个数。
21.×
【详解】略
22.0.63m
【详解】75cm=0.75m
0.84×0.75=0.63(m )
答:这排储物柜所占的空间是0.63m 立方米。
23.12米
【分析】根据长方体的体积公式求解即可。
【详解】0.48÷0.2÷0.2
=2.4÷0.2
=12(米)
答:这块钢材有12米长。
【点睛】本题主要考查长方体的体积公式灵活运用。
24.160立方厘米
【分析】根据题意,要求长方体的体积,必须要知道长方体的长、宽和高,用表面积减去上下两个底面面积,可求出剩下的四个侧面面积:分别为长乘高的两个面和宽乘高的两个面,则侧面积表示为:S=2ah+2bh,底面周长可以表示为:(a+b)×2,将侧面积公式变形为:S=2h(a+b),用四个面的面积除以底面周长可以求出长方体的高,再根据体积公式:V=Sh求出长方体体积即可。
【详解】四个侧面面积为:
184-20×2
=184-40
=144(平方厘米)
长方体高为:144÷18=8(厘米)
长方体体积为:20×8=160(立方厘米)
答:该长方体体积为160立方厘米。
【点睛】本题考查了长方体表面积和体积的计算,难度较大,主要是通过分析能求出长方体的高是解题的关键。
25.(1)201.6立方米 (2)135次
【分析】(1)先统一单位为“米”,长方体体积=长×宽×高,代入数据解答即可;
(2)用需要沙土总量除以每次可运图量,小数结果要进一位.
【详解】(1)4厘米=0.04米,90×56×0.04=201.6(立方米)
答:需要201.6立方米的沙土.
(2)201.6÷1.5=134.4(次)
134+1=135(次)
答:至少需要运135次.
26.0.7立方米; 35平方米
【详解】客厅的面积是
10×3.5=35(平方米)
2厘米=0.02(米)
所以,需要木材为
35×0.02=0.7(立方米)
答:至少需要木材0.7立方米.铺好要在地板上涂上油漆,油漆面积是35平方米.
答案第1页,共2页
答案第1页,共2页
(共26题,满分100分)
题号 一 二 三 四 总分
得分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.注意书写整洁
一、选择题
1.(如图)一个长6cm,宽与高都是4cm的长方体。将它挖掉一个棱长2cm的小正方体,它的表面积( ),体积( )。
A.比原来大; 比原来小 B.比原来小; 不变 C.不变; 不变 D.无法确定
2.一块正方体实心钢坯,棱长为6分米,工人师傅想把它锻造成一个高为3分米、宽为4分米的长方体实心钢坯,这个长方体实心钢坯的长是( )分米。
A.36 B.27 C.24 D.18
3.一个装有足够水的长方体容器,底面长4dm,宽2.5dm,放入一个棱长为2dm的小正方体铁块,使之完全浸没。水面会升高( )dm。
A. B.0.8 C.1.25 D.2.5
4.四个同学分别用12个大小相同的小正方体搭物体。这些物体的( )一定相等。
A.高 B.底面积 C.表面积 D.体积
5.一个正方体的棱长扩大3倍,它的体积就增加( )倍。
A.3 B.9 C.26 D.27
6.如图,把3个棱长为5cm的正方体拼接成一个长方体,这个长方体的表面积是( )cm2。
A.450 B.420 C.390 D.350
7.一个长方体的长不变,宽缩小到原来的,要想使长方体的体积不变,高要( )。
A.缩小到原来的 B.缩小到原来的
C.扩大到原来的3倍 D.扩大到原来的9倍
8.如图,甲和乙都是用4个同样大小的小正方体拼成的,下面的说法中,正确的是( )。
甲 乙
A.甲的体积大 B.乙的体积大
C.甲的体积与乙的体积相等 D.甲的表面积与乙的表面积相等
二、填空题
9.体积相等的长方体和正方体,表面积也一定相等. ( )
10.下图是一个( )体的盒子,它里面能装( )个这样的小正方体。
11.一个装有水的长方体容器,长2分米,宽1.8分米,高1.5分米。放入一个桃子后,水面升高0.25分米,这个桃子的体积是( )立方分米。
12.正方体的棱长是8分米,它的表面积是( )平方分米,体积是( )立方分米。
13.做一个长8分米,宽6分米,高5分米的长方体无盖玻璃鱼缸,用角钢做这个鱼缸的框架,至少需要角钢( )米,需要玻璃( )分米,最多能装水( )升。
14.一个正方体框架用了96厘米铁丝,它的棱长是( ),表面积是( ),体积是( )。
15.把一个正方体铁块浸没在一个棱长为3分米的正方体容器中(没有溢出)水面上升了5厘米,这个正方体铁块的体积是( )立方分米。
16.一个长方体底面是一个边长5厘米的正方形,前面的面积是40平方厘米。这个长方体的体积是( )立方厘米,表面积是( )平方厘米。
三、判断题
17.一个长方体的箱子能装6m 的货物,这个箱子的体积就是6m 。( )
18.正方体的棱长扩大2倍,则表面积和体积都扩大4倍。( )
19.棱长和相等的正方体与长方体的表面积不相等,但它们的体积相等。( )
20.棱长1分米的正方体最多可以截成5个棱长2厘米的小正方体。( )
21.是由体积是1立方厘米的小正方体组成的,它的体积是4立方厘米。( )
四、解答题
22.幼儿园有一排长方体储物柜,共占地0.84m ,储物柜的高均为75cm,这排储物柜所占的空间是多少立方米?
23.一块体积为0.48立方米的长方体钢材,底面是边长为0.2米的正方形,这块钢材有多长?
24.有一个长方体,表面积是184平方厘米,底面积是20平方厘米,底面周长是18厘米,这个长方体的体积是多少立方厘米?
25.在一块长90米,宽56米的长方形地上铺一层厚4厘米的沙土.
(1)需要多少沙土?
(2)一辆车每次运送1.5米3的沙土,至少需要运多少次?
26.在一个长为10米、宽为3.5米的长方形客厅的地面上铺设2厘米厚的木地板,至少需要木材多少立方米?铺好后要在地板上涂油漆,涂油漆部分的面积是多少?
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
) (
学校:___________姓名:___________班级:___________考号:___________
) (
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
第1页 共4页 ◎ 第2页 共4页
第1页 共4页 ◎ 第2页 共4页
参考答案:
1.A
【分析】由图意知:从长方体中挖掉一个棱长2cm的小正方体,少了小正方体的正面和上面,但又多了下面小正方体的上面和里面小正方体的正面、左右两个小正方体的左右侧面,也就是减少两个面,多了四个面,表面积变大;因少了一个小正方体,体积减少。据此解答。
【详解】由分析知:这个长方体的表面积多了两个小正方体的面,表面积增大,体积变小。
故答案为:A
【点睛】本题考查了长方体的表面积和体积、了解如上图挖掉一个小正方体,表面积增加了两个小正方体的面,体积变小是解答本题的关键。
2.D
【分析】把正方体实心钢坯锻造成长方体,体积不变;根据正方体体积公式:体积=棱长×棱长×棱长,代入数据,求出正方体实心钢胚的体积,再根据长方体体积公式:体积=长×宽×高;长=体积÷(宽×高),代入数据,即可解答。
【详解】6×6×6÷(4×3)
=36×6÷12
=216÷12
=18(分米)
一块正方体实心钢坯,棱长为6分米,工人师傅想把它锻造成一个高为3分米、宽为4分米的长方体实心钢坯,这个长方体实心钢坯的长是18分米。
故答案为:D
【点睛】熟练掌握和灵活运用长方体体积公式和正方体体积公式是解答本题的关键。
3.B
【分析】长方体容器中原来装有足够的水,而铁块本身具有一定的体积,放入水中后会占有一定的空间,导致水面上升,此时,水面升高所增加的水的体积就等于铁块的体积,则水面上升的高度=水面上升的体积÷长方体容器的底面积。
【详解】-
=8÷10
=0.8(dm)
故答案为:B
【点睛】解决这类问题,要特别注意两点:一是放入物体后水面是否溢出,二是物体是否完全浸入水中。
4.D
【分析】用12个大小相同的小正方体搭物体,无论搭成什么形状,体积都等于12个小正方体的体积之和,但是底面积、高和表面积都有可能发生变化,据此选择。
【详解】由分析可知,四个同学分别用12个大小相同的小正方体搭物体。这些物体的体积一定相等。
故选择:D
【点睛】此题考查了立体图形的切拼,明确物体的体积不会随着物体的形状发生变化。
5.C
【分析】根据正方体的体积公式:,再根据因数与积的变化规律,正方体的棱长扩大3倍,体积扩大27倍,所以它的体积增加(27-1)倍,据此解答。
【详解】一个正方体的棱长扩大3倍,它的体积就扩大倍
它的体积就增加
故答案为:C
【点睛】此题考查的目的是理解掌握正方体的体积公式。
6.D
【分析】3个正方体拼接一个长方体,长方体的长=正方体的棱长×3,长方体的宽=正方体的棱长,长方体的高=正方体的棱长,根据长方体的表面积公式:表面积=(长×宽+长×高+宽×高)×2,代入数据,即可解答。
【详解】长方体的长:5×3=15(cm),宽:5cm,高:5cm。
(15×5+15×5+5×5)×2
=(75+75+25)×2
=(150+25)×2
=175×2
=350(cm2)
故答案为:D
【点睛】本题考查立体图形的切拼,以及长方体表面积公式的应用,熟练掌握长方体表面积公式,是解答本题的关键。
7.C
【分析】根据长方体的体积=长×宽×高,依据积不变的规律可知,其中一个乘数缩小到原来的,如果要使积不变,那么另一个乘数扩大到原来的3倍。
【详解】根据分析可知,一个长方体的长不变,宽缩小到原来的,要想使长方体的体积不变,高要扩大到原来的3倍。
故答案为:C
【点睛】此题主要考查学生对长方体体积的认识与了解,也考查了积不变的规律。
8.C
【分析】由图可知:甲比原来4个小正方体减少6个正方形面,体积等于4个小正方体体积之和;乙比原来4个小正方体减少8个正方形面,体积等于4个小正方体体积之和;据此解答。
【详解】因为甲比原来4个小正方体减少6个正方形面;乙比原来4个小正方体减少8个正方形面,乙减少的多,所以甲的表面积大于乙的表面积;
甲的体积=等于4个小正方体体积之和=乙的体积,所以甲的体积与乙的体积相等。
故答案为:C
【点睛】本题主要考查立体图形的切拼,解题时要明确拼接时体积就不变。
9.×
【分析】长方体的体积=长×宽×高,正方体的体积=棱长×棱长×棱长,此题可以采用举例说明的方法进行判断.
【详解】一个长方体和正方体的体积相等,都是8,
所以正方体的棱长是2,表面积是2×2×6=24;
长方体的长宽高可以分别是:1、2、4,表面积是1×2×2+1×4×2+2×4×2,
=4+8+16,
=28,
所以原题说法错误.
故答案为×.
10. 长方 36
【分析】观察图可知,它是一个长方体的盒子,长方体的长是3,宽是4,高是3,即长方体的盒子里一行能摆3个小正方体,能摆4行,总共有3层。根据长方体的体积计算公式V=abh计算出能装多少个小正方体。
【详解】它是一个长方体的盒子
3×4×3
=12×3
=36(个)
【点睛】本题考查的是长方体体积计算公式的运用,熟练掌握它的体积并灵活运用。
11.0.9
【分析】根据题意可知,把桃子放入容器中,上升部分水的体积就等于桃子的体积,根据长方体的体积公式:V=abh,把数据代入公式解答。
【详解】2×1.8×0.25
=3.6×0.25
=0.9(立方分米)
【点睛】此题主要考查长方体的体积(容积)公式的灵活运用,关键是熟记公式。
12. 384 512
【分析】根据正方体的表面积公式:S=6a2,体积公式:V=a3,把数据分别代入公式解答。
【详解】8×8×6
=64×6
=384(平方分米);
8×8×8
=64×8
=512(立方分米);
【点睛】此题主要考查正方体的表面积公式、体积公式的灵活运用,关键是熟记公式。
13. 7.6 188 240
【分析】至少需要多少角钢,就是求长方体的棱长之和;
做这个鱼缸至少需要玻璃多少平方分米,就是求长方体5个面的面积;
鱼缸最多可以装水多少升,就是求长方体的体积,长方体的体积=长×宽×高。
【详解】(8+6+5)×4
=19×4
=76(分米)
=7.6(米)
8×6+(8×5+5×6)×2
=48+140
=188(分米)
8×6×5
=48×5
=240(分米3)
=240(升)
【点睛】考查了长方体的棱长、表面积、体积的实际应用,学生应掌握。
14. 8厘米 384平方厘米 512立方厘米
【分析】根据正方体的棱长总和=棱长×12,那么棱长=棱长总和÷12,据此求出棱长,再根据正方体的表面积公式:S=6a2,正方体的体积公式:V=a3,把数据代入公式解答。
【详解】96÷12=8(厘米)
8×8×6
=64×6
=384(平方厘米)
8×8×8
=64×8
=512(立方厘米)
【点睛】此题主要看正方体的棱长总和公式、表面积公式、体积公式的灵活运用,关键是熟记公式。
15.4.5
【分析】根据题意可知:容器中上升部分水的体积等于这个正方体铁块的体积,根据长方体的体积=底面积×高,求出这个正方体铁块的体积。
【详解】5厘米=0.5分米
3×3×0.5
=9×0.5
=4.5(立方分米)
【点睛】此题主要考查长方体的体积公式的灵活运用,关键是熟记公式。
16. 200 210
【分析】前面的面积=长×高,由此可以求出高,再根据长方体的体积公式、表面积公式解答即可。
【详解】40÷5=8(厘米)
5×5×8
=25×8
=200(立方厘米)
5×5×2+5×8×4
=50+160
=210(平方厘米)
【点睛】此题主要考查长方体的体积公式、表面积公式的灵活运用,关键是熟记公式。
17.×
【分析】物体的体积是指物体所占空间的大小,物体的容积是指物体所能容纳物体的大小,求物体的体积从物体外面测量有关数据,而容积是从里面测量有关数据。
【详解】根据分析可知,一个长方体的箱子能装6m 的货物,这个箱子的容积就是6m ,体积要大于容积。
故答案为:×
【点睛】本题是考查体积和容积的意义,注意,体积和容积是两个不同的概念,有计时容器的壁较薄可能忽略不计,但不是说物体的体积就是容积。
18.×
【分析】根据正方体的表面积公式:S=6a2,再根据因数与积的变化规律,积扩大的倍数等于因数扩大倍数的乘积,据此判断即可。
【详解】正方体的棱长扩大2倍,它的表面积就扩大倍。
体积扩大倍。
因此,正方体的棱长扩大2倍,则表面积和体积都扩大4倍。这种说法是错误的。
故答案为:×
【点睛】此题考查的目的是理解掌握正方体的表面积公式、因数与积的变化规律及应用。
19.×
【详解】略
20.×
【分析】把1分米化成10厘米,10÷2=5,大正方体的每条棱上都可截得5个棱长为2厘米的小正方体,所以一共可以截得5×5×5=125个小正方体。据此判断。
【详解】根据分析可得:
1分米=10厘米
10÷2=5(个)
所以5×5×5=125(个)
故答案为:×
【点睛】本题也可以利用大正方体的体积除以小正方体的体积求出切割出的小正方体的总个数。
21.×
【详解】略
22.0.63m
【详解】75cm=0.75m
0.84×0.75=0.63(m )
答:这排储物柜所占的空间是0.63m 立方米。
23.12米
【分析】根据长方体的体积公式求解即可。
【详解】0.48÷0.2÷0.2
=2.4÷0.2
=12(米)
答:这块钢材有12米长。
【点睛】本题主要考查长方体的体积公式灵活运用。
24.160立方厘米
【分析】根据题意,要求长方体的体积,必须要知道长方体的长、宽和高,用表面积减去上下两个底面面积,可求出剩下的四个侧面面积:分别为长乘高的两个面和宽乘高的两个面,则侧面积表示为:S=2ah+2bh,底面周长可以表示为:(a+b)×2,将侧面积公式变形为:S=2h(a+b),用四个面的面积除以底面周长可以求出长方体的高,再根据体积公式:V=Sh求出长方体体积即可。
【详解】四个侧面面积为:
184-20×2
=184-40
=144(平方厘米)
长方体高为:144÷18=8(厘米)
长方体体积为:20×8=160(立方厘米)
答:该长方体体积为160立方厘米。
【点睛】本题考查了长方体表面积和体积的计算,难度较大,主要是通过分析能求出长方体的高是解题的关键。
25.(1)201.6立方米 (2)135次
【分析】(1)先统一单位为“米”,长方体体积=长×宽×高,代入数据解答即可;
(2)用需要沙土总量除以每次可运图量,小数结果要进一位.
【详解】(1)4厘米=0.04米,90×56×0.04=201.6(立方米)
答:需要201.6立方米的沙土.
(2)201.6÷1.5=134.4(次)
134+1=135(次)
答:至少需要运135次.
26.0.7立方米; 35平方米
【详解】客厅的面积是
10×3.5=35(平方米)
2厘米=0.02(米)
所以,需要木材为
35×0.02=0.7(立方米)
答:至少需要木材0.7立方米.铺好要在地板上涂上油漆,油漆面积是35平方米.
答案第1页,共2页
答案第1页,共2页
