初中数学人教版八年级下册18.1平行四边形同步练习(含解析)
文档属性
| 名称 | 初中数学人教版八年级下册18.1平行四边形同步练习(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 214.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-04 00:00:00 | ||
图片预览


文档简介
人教版八年级下册18.1平行四边形
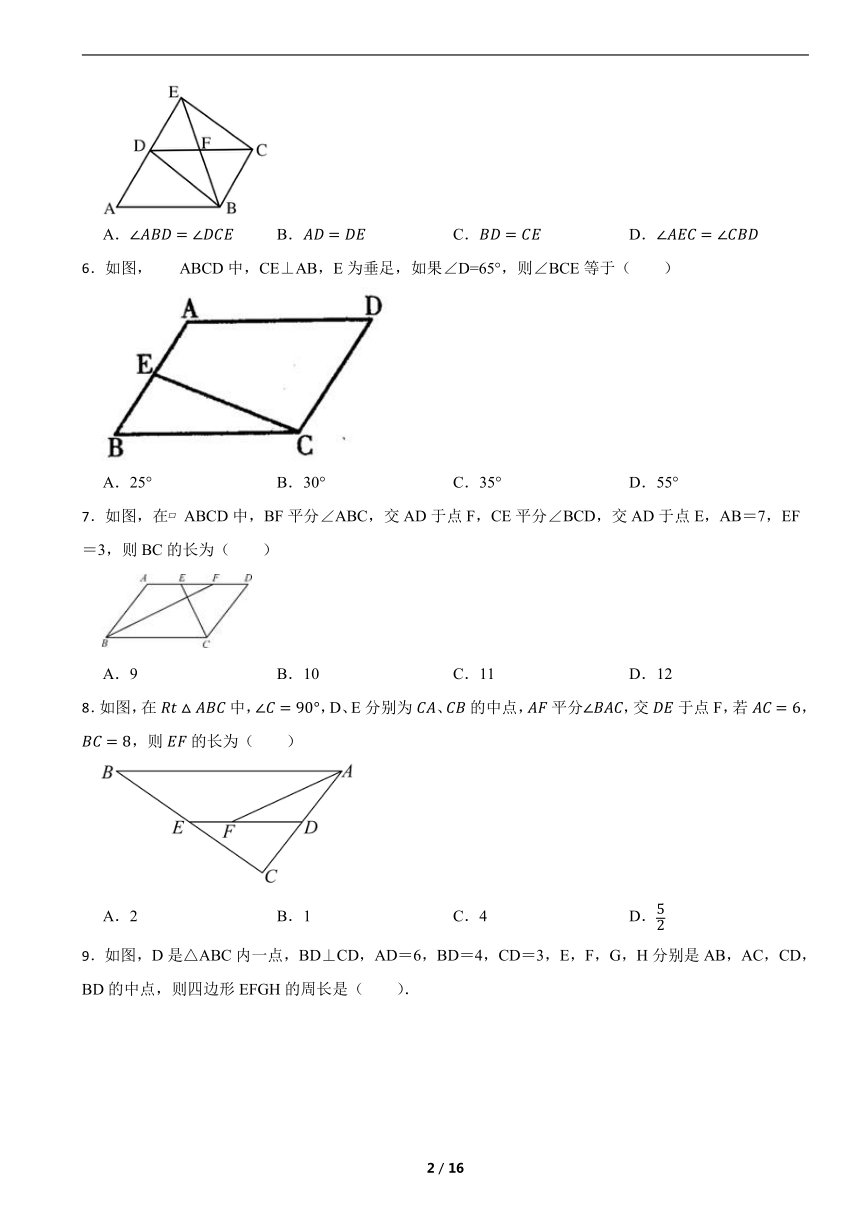
一、单选题
1.下列不能作为判定四边形ABCD为平行四边形的条件的是( )
A.AB=CD,AD=BC B.AB CD
C.AB=CD,AD∥BC D.AB∥CD,AD∥BC
2.如图矩形的对角线,相交于点,,,若,则四边形的周长是( )
A.4 B.6 C.8 D.10
3.如图,要测量池塘两侧的两点A、B之间的距离,可以取一个能直接到达A、B的点C,连结CA、CB,分别在线段CA、CB上取中点D、E,连结DE,测得DE=35m,则可得A、B之间的距离为( )
A.30m B.70m C.105m D.140m
4.如图是一个由5张纸片拼成的平行四边形,相邻纸片之间互不重叠也无缝隙,其中两张等腰直角三角形纸片的面积都为S1,另两张直角三角形纸片的面积都为S2,中间一张正方形纸片的面积为S3,则这个平行四边形的面积一定可以表示为( )
A.4S1 B.4S2 C.4S2+S3 D.3S1+4S3
5.如图,E是的边延长线上一点,连接,,,交于点F,添加以下条件,不能判定四边形为平行四边形的是( )
A. B. C. D.
6.如图, ABCD中,CE⊥AB,E为垂足,如果∠D=65°,则∠BCE等于( )
A.25° B.30° C.35° D.55°
7.如图,在 ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,AB=7,EF=3,则BC的长为( )
A.9 B.10 C.11 D.12
8.如图,在中,,D、E分别为、的中点,平分,交于点F,若,,则的长为( )
A.2 B.1 C.4 D.
9.如图,D是△ABC内一点,BD⊥CD,AD=6,BD=4,CD=3,E,F,G,H分别是AB,AC,CD,BD的中点,则四边形EFGH的周长是( ).
A.12 B.11 C.10 D.9
10.如图中,,,,为的中线,点、点分别为线段、上的动点,连接、,则的最小值为( )
A. B. C. D.
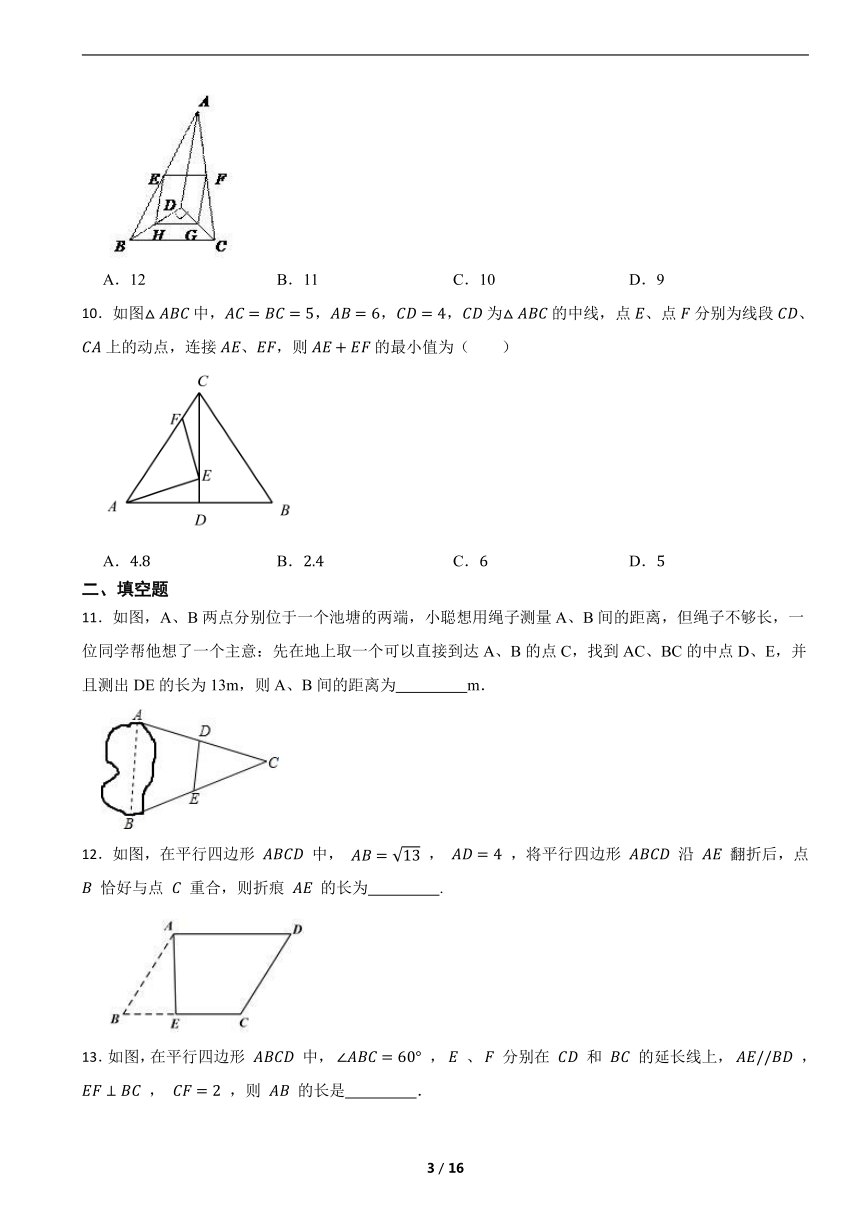
二、填空题
11.如图,A、B两点分别位于一个池塘的两端,小聪想用绳子测量A、B间的距离,但绳子不够长,一位同学帮他想了一个主意:先在地上取一个可以直接到达A、B的点C,找到AC、BC的中点D、E,并且测出DE的长为13m,则A、B间的距离为 m.
12.如图,在平行四边形 中, , ,将平行四边形 沿 翻折后,点 恰好与点 重合,则折痕 的长为 .
13.如图,在平行四边形 中, , 、 分别在 和 的延长线上, , , ,则 的长是 .
14.如图,平行四边形ABCD的对角线AC与BD相交于点O,按以下步骤作图:①以点A为圆心,以任意长为半径作弧,分别交AO,AB于点M,N;②以点O为圆心,以AM长为半径作弧,交OC于点M';③以点M'为圆心,以MN长为半径作弧,在∠COB内部交前面的弧于点N';④过点N'作射线ON'交BC于点E.若AB=8,则线段OE的长为 .
15.如图,在 ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论中一定成立的是 (把所有正确结论的序号都填在横线上)
①∠DCF= ∠BCD;②EF=CF;③S△BEC=2S△CEF;④∠DFE=3∠AEF.
16.如图,在 ABCD中,AD=3cm,动点P以每秒0.5cm的速度从点A向点D运动,另一动点Q以每秒1cm的速度从点C出发,在BC间往返运动,P、Q两点同时出发,当点P到达点D时停止运动(同时Q点也停止),若P,D,Q,B四点组成的四边形是平行四边形时,则运动时间为
秒.
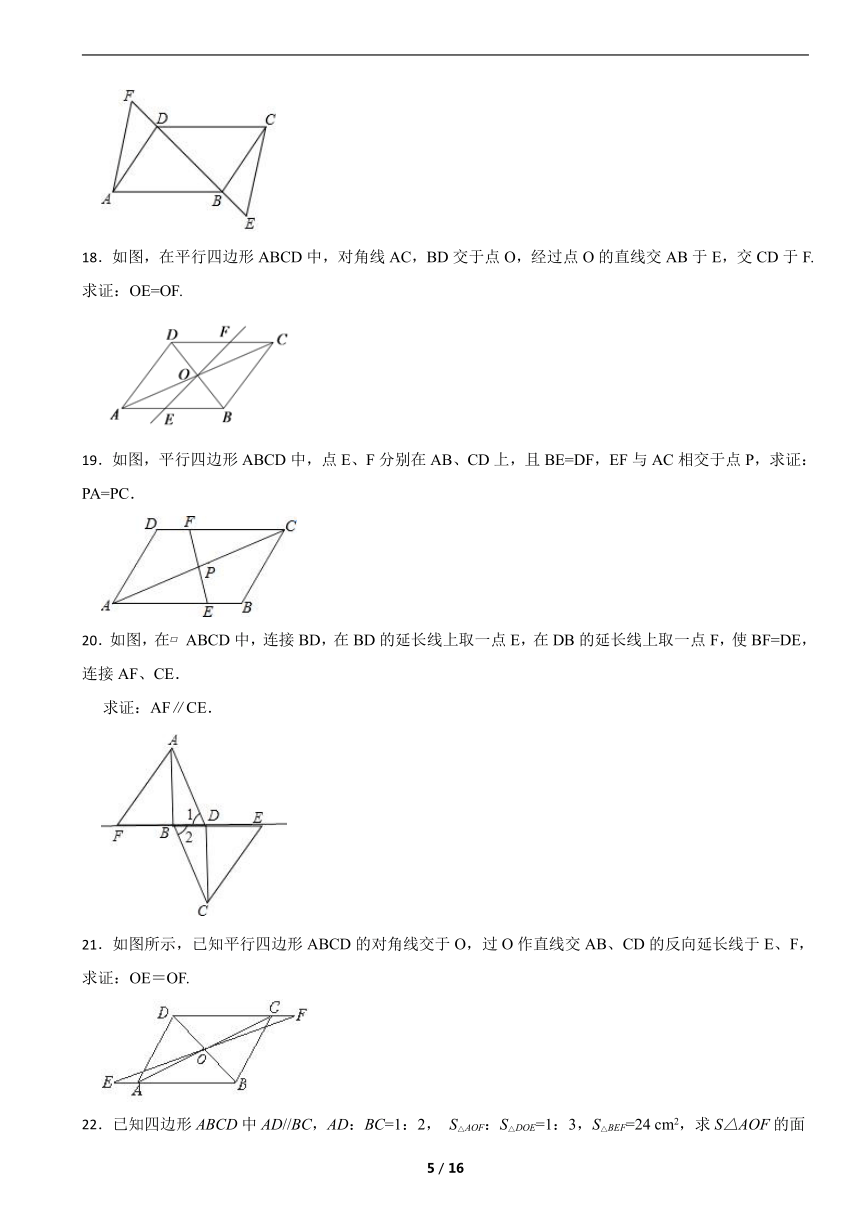
三、解答题
17.如图,四边形ABCD为平行四边形,E,F是直线BD上两点,且BE=DF,连接AF,CE求证:AF=CE.
18.如图,在平行四边形ABCD中,对角线AC,BD交于点O,经过点O的直线交AB于E,交CD于F. 求证:OE=OF.
19.如图,平行四边形ABCD中,点E、F分别在AB、CD上,且BE=DF,EF与AC相交于点P,求证:PA=PC.
20.如图,在 ABCD中,连接BD,在BD的延长线上取一点E,在DB的延长线上取一点F,使BF=DE,连接AF、CE.
求证:AF∥CE.
21.如图所示,已知平行四边形ABCD的对角线交于O,过O作直线交AB、CD的反向延长线于E、F,求证:OE=OF.
22.已知四边形ABCD中AD//BC,AD:BC=1:2, S△AOF:S△DOE=1:3,S△BEF=24 cm2,求S△AOF的面积。
答案解析部分
1.【答案】C
【解析】【解答】解:A.∵AB=CD,AD=BC,∴四边形ABCD的两组对边相等,可以判定四边形ABCD是平行四边形;故不符合题意;
B.∵AB∥CD,AB=CD,∴四边形ABCD的一组对边平行且相等,可以判定四边形ABCD是平行四边形;故不符合题意;
C.∵AB=CD,AD∥CD,无法判定四边形ABCD是平行四边形;故符合题意;
D.∵AB∥CD,AD∥BC,四边形ABCD的两组对边分别平行,四边形ABCD是平行四边形;故不符合题意.
故答案为:C.
【分析】平行四边形的判定方法:①四边形的两组对边分别相等,四边形是平行四边形;②四边形的一组对边平行且相等,四边形是平行四边形;③四边形的两组对边分别平行,四边形是平行四边形;四边形的对角线互相平分,四边形为平行四边形.
2.【答案】C
【解析】【解答】解:
∵,
∴四边形CODE是平行四边形
∵OC=OD=12BD=2
∴平行四边形CODE是菱形
∴CODE的周长是24=8
故答案为:C
【分析】熟练掌握平行四边形、矩形、菱形的判定定理。
3.【答案】B
【解析】【解答】解:∵D、E分别是AC、BC的中点,
∴DE是△ABC的中位线,
根据三角形的中位线定理,得:AB=2DE=70m.
故答案为:B.
【分析】由D,E分别是边AC,AB的中点,首先判定DE是三角形的中位线,然后根据三角形的中位线定理求得AB的长即可.
4.【答案】A
【解析】【解答】解:设等腰直角三角形的直角边为a,正方形边长为c,
则S2= (a+c)(a﹣c)= a2﹣ c2,
∴S2=S1﹣ S3,
∴S3=2S1﹣2S2,
∴平行四边形面积=2S1+2S2+S3=2S1+2S2+2S1﹣2S2=4S1.
故选A.
【分析】设等腰直角三角形的直角边为a,正方形边长为c,求出S2(用a、c表示),得出S1,S2,S3之间的关系,由此即可解决问题.
5.【答案】C
【解析】【解答】解:A、∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴DE∥BC,∠ABD=∠CDB,
∵∠ABD=∠DCE,
∴∠DCE=∠CDB,
∴BD∥CE,
∴四边形BCED为平行四边形,故A不符合题意;
B、∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∵,
∴ED=CB,
∴四边形BCED为平行四边形,故B不符合题意;
C、∵四边形ABCD是平行四边形,
∴AD∥BC,
根据
,不能判定四边形BCED为平行四边形;故C符合题意;
D、∵AE∥BC,
∴∠DEC+∠BCE=∠EDB+∠DBC=180°,
∵∠AEC=∠CBD,
∴∠BDE=∠BCE,
∴四边形BCED为平行四边形,故D不符合题意,
故答案为:C.
【分析】根据平行四边形的判定方法逐项判断即可。
6.【答案】A
【解析】【解答】解:∵四边形ABCD是平行四边形,
∴∠B=∠D=65°,
∵CE⊥AB,
∴∠BEC=90°,
∴∠BCE=90° ∠B=25°.
故答案为:A.
【分析】先根据平行四边形的性质得到∠B=∠D=65°,进而根据垂直即可求解.
7.【答案】C
【解析】【解答】∵四边形ABCD是平行四边形,∴AB=CD=7,BC=AD,AD∥BC.
∵BF平分∠ABC交AD于F,CE平分∠BCD交AD于E,∴∠ABF=∠CBF=∠AFB,∠BCE=∠DCE=∠CED,∴AB=AF=7,DC=DE=7,∴EF=AF+DE﹣AD=7+7﹣AD=3,∴AD=11,∴BC=11.
故答案为:C.
【分析】先证明AB=AF=7,DC=DE,再根据EF=AF+DE﹣AD求出AD,即可得出答案.
8.【答案】A
【解析】【解答】解:在Rt△ABC中,∠C=90°,AC=6,BC=8,
∴AB=
=
=10
∵D、E分别为CA、CB的中点
∴DE是△ABC的中位线
∴DE=AB=5,DE//AB
∴∠AFD=∠BAF
∵AF平分∠BAC
∴∠DAF=∠BAF
∴∠DAF=∠AFD
∴DF=AD=AC=×6=3
∴EF=DE-DF=5-3=2
故答案为:A.
【分析】根据勾股定理求出AB的长,再根据三角形中位线定理求出DE的长和DE∥AB,然后根据平行线的性质并结合角平分线的定义看得到∠DAF=∠DFA,进而得到DF=AD,即可求出EF的长。
9.【答案】B
【解析】【解答】∵BD⊥DC,BD=4,CD=3,
由勾股定理得: ,
∵E、F、G、H分别是AB、AC、CD、BD的中点,
, ,
∴四边形EFGH的周长是EF+FG+HG+EH=2×(2.5+3)=11.
答案为:B.
【分析】先用勾股定理求出BC,利用中位线定理得 E F = B C = 2.5, EH=FG=AD=3,进而求出周长.
10.【答案】A
【解析】【解答】解:连接,过B点作于N点,如图,
∵中,,,为的中线,
∴,,
∴垂直平分,
∴,
∴根据垂线段最短可知:当B、E、F三点共线,且此线与垂直时有最小值,
∴的最小值为的长,
∵,,
∴,
∴,
∵,,,
∴,
∴的最小值为,
故选:A.
【分析】连接,过B点作于N点,根据三角形中位线定理可得垂直平分,则,根据垂线段最短可得当B、E、F三点共线,且此线与垂直时有最小值,再根据三角形面积公式可得,再代入值即可求出答案.
11.【答案】26
【解析】【解答】解:∵D,E分别是AC,BC的中点,
∴AB=2DE=26m.
故答案为:26.
【分析】易得DE是△ABC的中位线,根据三角形中位线等于第三边的一半即可求解.
12.【答案】3
【解析】【解答】解:点 恰好与点 重合,且四边形 是平行四边形,根据翻折的性质, 则 , ,在 中,由勾股定理得
故答案为:3.
【分析】根据翻折可知,,在直角三角形ABE中利用勾股定理即可求得AE长.
13.【答案】2
【解析】【解答】解:∵四边形ABCD是平行四边形,
∴AB∥DC,AB=CD.
∵AE∥BD,
∴四边形ABDE是平行四边形.
∴AB=DE=CD= CE.
∵EF⊥BC,
∴∠EFC=90°.
∵AB∥CD,
∴∠ECF=∠ABC=60°.
∴∠CEF=30°.
∴CF= CE.
∵CF=2,
∴AB=CF=2.
故答案为:2.
【分析】根据平行四边形的判定定理可得出四边形ABDE是平行四边形,得出AB=DE=CD= CE.由EF⊥BC,AB∥CD,得出∠ECF=∠ABC=60°,∠CEF=30°,CF= CE,由CF=2,即可得出 的长 。
14.【答案】4
【解析】【解答】解:由作法得∠COE=∠OAB,
∴OE∥AB,
∵四边形ABCD为平行四边形,
∴OC=OA,
∴CE=BE,
∴OE为△ABC的中位线,
∴OE= AB= ×8=4.
故答案为4.
【分析】利用作法得到∠COE=∠OAB,则OE//AB,利用平行四边形的性质判断OE为△A BC的中位线,从而得到OE的长.
15.【答案】①②④.
【解析】【解答】①∵F是AD的中点,
∴AF=FD,
∵在 ABCD中,AD=2AB,
∴AF=FD=CD,
∴∠DFC=∠DCF,
∵AD∥BC,
∴∠DFC=∠FCB,
∴∠DCF=∠BCF,
∴∠DCF= ∠BCD,故此选项正确;
延长EF,交CD延长线于M,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠A=∠MDF,
∵F为AD中点,
∴AF=FD,
在△AEF和△DFM中,
,
∴△AEF≌△DMF(ASA),
∴FE=MF,∠AEF=∠M,
∵CE⊥AB,
∴∠AEC=90°,
∴∠AEC=∠ECD=90°,
∵FM=EF,
∴FC=FM,故②正确;
③∵EF=FM,
∴S△EFC=S△CFM,
∵MC>BE,
∴S△BEC<2S△EFC
故S△BEC=2S△CEF错误;
④设∠FEC=x,则∠FCE=x,
∴∠DCF=∠DFC=90°-x,
∴∠EFC=180°-2x,
∴∠EFD=90°-x+180°-2x=270°-3x,
∵∠AEF=90°-x,
∴∠DFE=3∠AEF,故此选项正确.
16.【答案】4
【解析】【解答】解:∵四边形ABCD是平行四边形,
∴AD∥BC,BC=AD=3cm,
若以P,D,Q,B四点组成的四边形是平行四边形,则PD=BQ,
设运动时间为t秒,当点Q从C到B过程中,
则AP=0.5t,CQ=t,PD=3-0.5t,BQ=3-t,
∴3-0.5t=3-t,
解得:t=0,不合题意;
当点P到达B返回过程中,PD=3-0.5t,BQ=t-3,
∴3-0.5t=t-3,
解得:t=4,
∴当运动时间为4时,以P,D,Q,B四点组成的四边形是平行四边形 ;
故答案为:4.
【分析】由PD∥BQ,可知以P,D,Q,B四点组成的四边形是平行四边形时,则PD=BQ,设运动时间为t秒,分两种情况:当点Q从C到B过程中和当点P到达B返回过程中,据此分别列出方程并求解即可.
17.【答案】解:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴∠ADB=∠DBC,
∵∠ADF+∠ADB=180°,∠CBE+∠DBC=180°,
∴∠ADF=∠CBE,
∵DF=BE,
∴△ADF≌△CBE,
∴AF=CE.
【解析】【分析】根据平行四边形的性质得出 AD∥BC,AD=BC, 根据二直线平行,内错角相等得出 ∠ADB=∠DBC, 进而根据等角的补角相等得出 ∠ADF=∠CBE, 从而利用SAS判断出 △ADF≌△CBE, 根据全等三角形的对应边相等得出 AF=CE.
18.【答案】证明:∵四边形ABCD是平行四边形,∴OA=OC,AB∥CD 。∴∠OAE=∠OCF 。∵∠AOE=∠COF ,∴△OAE≌△OCF(ASA)。∴OE=OF。
【解析】【分析】根据平行四边形的性质得出OA=OC,AB∥CD ,可证得∠OAE=∠OCF,再利用ASA证明△OAE≌△OCF,然后利用全等三角形的性质即可证得结论。
19.【答案】证明:连接AF,CE,
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵BE=DF,
∴AB﹣BE=CD﹣DF,
∴AE=CF,
∴四边形AECF是平行四边形,
∴PA=PC.
【解析】【分析】首先连接AF,CE,由四边形ABCD是平行四边形,可得AB∥CD,AB=CD,又由BE=DF,证得AE=CF,即可证得四边形AECF是平行四边形,继而证得结论.
20.【答案】证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴∠1=∠2,
∵BF=DE,
∴BF+BD=DE+BD,
即DF=BE,
在△ADF和△CBE中,
,
∴△ADF≌△CBE(SAS),
∴∠AFD=∠CEB,
∴AF∥CE.
【解析】【分析】由平行四边形的性质得出AD∥BC,AD=BC,证出∠1=∠2,DF=BE,由SAS证明△ADF≌△CBE,得出对应角相等,再由平行线的判定即可得出结论.本题考查了平行四边形的性质,全等三角形的判定与性质、平行线的性质;熟练掌握平行四边形的性质,证明三角形全等是解决问题的关键.
21.【答案】证明:∵四边形ABCD是平行四边形ABCD,
∴OA=OC,DF∥EB
∴∠E=∠F
又∵∠EOA=∠FOC
∴△OAE≌△OCF,∴OE=OF
【解析】【分析】本题考查平行四边形的性质.掌握平行四边形对边相等、对角线互相平分的性质,同时结合此前学过的证明线段相等的方法,就能解答本题
22.【答案】6
【解析】【解答】解 :如图,取BC的中点G,连接DG、EG、FG.
∵ AD∶BC=1∶2 ;G是BC的中点,
∴ BG=AD ;
又∵AD//BC ;
∴四边形ABGD是平行四边形;
∴S△ADE+S△BEG=S平行四边形ABDG
S△AFD+S△BG=S平行四边形ABDG
∴上面两个三角形的面积差与下面两个三角形面积差相等。
∵上面两个三角形面积差相当于图中△OAF和△ODE的面积之差,是△AOF的2倍。
下面两个三角形面积差是(S△BEC+24)÷2 S△BEC÷2=12
∴S△AOF=12÷2=6m2.
【分析】如图,取BC的中点G,连接DG、EG、FG.根据一组对边平行且相等的四边形是平行四边形得出四边形ABGD是平行四边形; 根据平行四边形的面积公式,三角形的面积计算公式得出S△ADE+S△BEG=S平行四边形ABDG,S△AFD+S△BG=S平行四边形ABDG;从而得出上面两个三角形的面积差与下面两个三角形面积差相等;进而得出上面两个三角形面积差相当于图中△OAF和△ODE的面积之差,是△AOF的2倍;下面两个三角形面积差是(S△BEC+24)÷2 S△BEC÷2=12;从而得出答案。
1 / 1
一、单选题
1.下列不能作为判定四边形ABCD为平行四边形的条件的是( )
A.AB=CD,AD=BC B.AB CD
C.AB=CD,AD∥BC D.AB∥CD,AD∥BC
2.如图矩形的对角线,相交于点,,,若,则四边形的周长是( )
A.4 B.6 C.8 D.10
3.如图,要测量池塘两侧的两点A、B之间的距离,可以取一个能直接到达A、B的点C,连结CA、CB,分别在线段CA、CB上取中点D、E,连结DE,测得DE=35m,则可得A、B之间的距离为( )
A.30m B.70m C.105m D.140m
4.如图是一个由5张纸片拼成的平行四边形,相邻纸片之间互不重叠也无缝隙,其中两张等腰直角三角形纸片的面积都为S1,另两张直角三角形纸片的面积都为S2,中间一张正方形纸片的面积为S3,则这个平行四边形的面积一定可以表示为( )
A.4S1 B.4S2 C.4S2+S3 D.3S1+4S3
5.如图,E是的边延长线上一点,连接,,,交于点F,添加以下条件,不能判定四边形为平行四边形的是( )
A. B. C. D.
6.如图, ABCD中,CE⊥AB,E为垂足,如果∠D=65°,则∠BCE等于( )
A.25° B.30° C.35° D.55°
7.如图,在 ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,AB=7,EF=3,则BC的长为( )
A.9 B.10 C.11 D.12
8.如图,在中,,D、E分别为、的中点,平分,交于点F,若,,则的长为( )
A.2 B.1 C.4 D.
9.如图,D是△ABC内一点,BD⊥CD,AD=6,BD=4,CD=3,E,F,G,H分别是AB,AC,CD,BD的中点,则四边形EFGH的周长是( ).
A.12 B.11 C.10 D.9
10.如图中,,,,为的中线,点、点分别为线段、上的动点,连接、,则的最小值为( )
A. B. C. D.
二、填空题
11.如图,A、B两点分别位于一个池塘的两端,小聪想用绳子测量A、B间的距离,但绳子不够长,一位同学帮他想了一个主意:先在地上取一个可以直接到达A、B的点C,找到AC、BC的中点D、E,并且测出DE的长为13m,则A、B间的距离为 m.
12.如图,在平行四边形 中, , ,将平行四边形 沿 翻折后,点 恰好与点 重合,则折痕 的长为 .
13.如图,在平行四边形 中, , 、 分别在 和 的延长线上, , , ,则 的长是 .
14.如图,平行四边形ABCD的对角线AC与BD相交于点O,按以下步骤作图:①以点A为圆心,以任意长为半径作弧,分别交AO,AB于点M,N;②以点O为圆心,以AM长为半径作弧,交OC于点M';③以点M'为圆心,以MN长为半径作弧,在∠COB内部交前面的弧于点N';④过点N'作射线ON'交BC于点E.若AB=8,则线段OE的长为 .
15.如图,在 ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论中一定成立的是 (把所有正确结论的序号都填在横线上)
①∠DCF= ∠BCD;②EF=CF;③S△BEC=2S△CEF;④∠DFE=3∠AEF.
16.如图,在 ABCD中,AD=3cm,动点P以每秒0.5cm的速度从点A向点D运动,另一动点Q以每秒1cm的速度从点C出发,在BC间往返运动,P、Q两点同时出发,当点P到达点D时停止运动(同时Q点也停止),若P,D,Q,B四点组成的四边形是平行四边形时,则运动时间为
秒.
三、解答题
17.如图,四边形ABCD为平行四边形,E,F是直线BD上两点,且BE=DF,连接AF,CE求证:AF=CE.
18.如图,在平行四边形ABCD中,对角线AC,BD交于点O,经过点O的直线交AB于E,交CD于F. 求证:OE=OF.
19.如图,平行四边形ABCD中,点E、F分别在AB、CD上,且BE=DF,EF与AC相交于点P,求证:PA=PC.
20.如图,在 ABCD中,连接BD,在BD的延长线上取一点E,在DB的延长线上取一点F,使BF=DE,连接AF、CE.
求证:AF∥CE.
21.如图所示,已知平行四边形ABCD的对角线交于O,过O作直线交AB、CD的反向延长线于E、F,求证:OE=OF.
22.已知四边形ABCD中AD//BC,AD:BC=1:2, S△AOF:S△DOE=1:3,S△BEF=24 cm2,求S△AOF的面积。
答案解析部分
1.【答案】C
【解析】【解答】解:A.∵AB=CD,AD=BC,∴四边形ABCD的两组对边相等,可以判定四边形ABCD是平行四边形;故不符合题意;
B.∵AB∥CD,AB=CD,∴四边形ABCD的一组对边平行且相等,可以判定四边形ABCD是平行四边形;故不符合题意;
C.∵AB=CD,AD∥CD,无法判定四边形ABCD是平行四边形;故符合题意;
D.∵AB∥CD,AD∥BC,四边形ABCD的两组对边分别平行,四边形ABCD是平行四边形;故不符合题意.
故答案为:C.
【分析】平行四边形的判定方法:①四边形的两组对边分别相等,四边形是平行四边形;②四边形的一组对边平行且相等,四边形是平行四边形;③四边形的两组对边分别平行,四边形是平行四边形;四边形的对角线互相平分,四边形为平行四边形.
2.【答案】C
【解析】【解答】解:
∵,
∴四边形CODE是平行四边形
∵OC=OD=12BD=2
∴平行四边形CODE是菱形
∴CODE的周长是24=8
故答案为:C
【分析】熟练掌握平行四边形、矩形、菱形的判定定理。
3.【答案】B
【解析】【解答】解:∵D、E分别是AC、BC的中点,
∴DE是△ABC的中位线,
根据三角形的中位线定理,得:AB=2DE=70m.
故答案为:B.
【分析】由D,E分别是边AC,AB的中点,首先判定DE是三角形的中位线,然后根据三角形的中位线定理求得AB的长即可.
4.【答案】A
【解析】【解答】解:设等腰直角三角形的直角边为a,正方形边长为c,
则S2= (a+c)(a﹣c)= a2﹣ c2,
∴S2=S1﹣ S3,
∴S3=2S1﹣2S2,
∴平行四边形面积=2S1+2S2+S3=2S1+2S2+2S1﹣2S2=4S1.
故选A.
【分析】设等腰直角三角形的直角边为a,正方形边长为c,求出S2(用a、c表示),得出S1,S2,S3之间的关系,由此即可解决问题.
5.【答案】C
【解析】【解答】解:A、∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴DE∥BC,∠ABD=∠CDB,
∵∠ABD=∠DCE,
∴∠DCE=∠CDB,
∴BD∥CE,
∴四边形BCED为平行四边形,故A不符合题意;
B、∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∵,
∴ED=CB,
∴四边形BCED为平行四边形,故B不符合题意;
C、∵四边形ABCD是平行四边形,
∴AD∥BC,
根据
,不能判定四边形BCED为平行四边形;故C符合题意;
D、∵AE∥BC,
∴∠DEC+∠BCE=∠EDB+∠DBC=180°,
∵∠AEC=∠CBD,
∴∠BDE=∠BCE,
∴四边形BCED为平行四边形,故D不符合题意,
故答案为:C.
【分析】根据平行四边形的判定方法逐项判断即可。
6.【答案】A
【解析】【解答】解:∵四边形ABCD是平行四边形,
∴∠B=∠D=65°,
∵CE⊥AB,
∴∠BEC=90°,
∴∠BCE=90° ∠B=25°.
故答案为:A.
【分析】先根据平行四边形的性质得到∠B=∠D=65°,进而根据垂直即可求解.
7.【答案】C
【解析】【解答】∵四边形ABCD是平行四边形,∴AB=CD=7,BC=AD,AD∥BC.
∵BF平分∠ABC交AD于F,CE平分∠BCD交AD于E,∴∠ABF=∠CBF=∠AFB,∠BCE=∠DCE=∠CED,∴AB=AF=7,DC=DE=7,∴EF=AF+DE﹣AD=7+7﹣AD=3,∴AD=11,∴BC=11.
故答案为:C.
【分析】先证明AB=AF=7,DC=DE,再根据EF=AF+DE﹣AD求出AD,即可得出答案.
8.【答案】A
【解析】【解答】解:在Rt△ABC中,∠C=90°,AC=6,BC=8,
∴AB=
=
=10
∵D、E分别为CA、CB的中点
∴DE是△ABC的中位线
∴DE=AB=5,DE//AB
∴∠AFD=∠BAF
∵AF平分∠BAC
∴∠DAF=∠BAF
∴∠DAF=∠AFD
∴DF=AD=AC=×6=3
∴EF=DE-DF=5-3=2
故答案为:A.
【分析】根据勾股定理求出AB的长,再根据三角形中位线定理求出DE的长和DE∥AB,然后根据平行线的性质并结合角平分线的定义看得到∠DAF=∠DFA,进而得到DF=AD,即可求出EF的长。
9.【答案】B
【解析】【解答】∵BD⊥DC,BD=4,CD=3,
由勾股定理得: ,
∵E、F、G、H分别是AB、AC、CD、BD的中点,
, ,
∴四边形EFGH的周长是EF+FG+HG+EH=2×(2.5+3)=11.
答案为:B.
【分析】先用勾股定理求出BC,利用中位线定理得 E F = B C = 2.5, EH=FG=AD=3,进而求出周长.
10.【答案】A
【解析】【解答】解:连接,过B点作于N点,如图,
∵中,,,为的中线,
∴,,
∴垂直平分,
∴,
∴根据垂线段最短可知:当B、E、F三点共线,且此线与垂直时有最小值,
∴的最小值为的长,
∵,,
∴,
∴,
∵,,,
∴,
∴的最小值为,
故选:A.
【分析】连接,过B点作于N点,根据三角形中位线定理可得垂直平分,则,根据垂线段最短可得当B、E、F三点共线,且此线与垂直时有最小值,再根据三角形面积公式可得,再代入值即可求出答案.
11.【答案】26
【解析】【解答】解:∵D,E分别是AC,BC的中点,
∴AB=2DE=26m.
故答案为:26.
【分析】易得DE是△ABC的中位线,根据三角形中位线等于第三边的一半即可求解.
12.【答案】3
【解析】【解答】解:点 恰好与点 重合,且四边形 是平行四边形,根据翻折的性质, 则 , ,在 中,由勾股定理得
故答案为:3.
【分析】根据翻折可知,,在直角三角形ABE中利用勾股定理即可求得AE长.
13.【答案】2
【解析】【解答】解:∵四边形ABCD是平行四边形,
∴AB∥DC,AB=CD.
∵AE∥BD,
∴四边形ABDE是平行四边形.
∴AB=DE=CD= CE.
∵EF⊥BC,
∴∠EFC=90°.
∵AB∥CD,
∴∠ECF=∠ABC=60°.
∴∠CEF=30°.
∴CF= CE.
∵CF=2,
∴AB=CF=2.
故答案为:2.
【分析】根据平行四边形的判定定理可得出四边形ABDE是平行四边形,得出AB=DE=CD= CE.由EF⊥BC,AB∥CD,得出∠ECF=∠ABC=60°,∠CEF=30°,CF= CE,由CF=2,即可得出 的长 。
14.【答案】4
【解析】【解答】解:由作法得∠COE=∠OAB,
∴OE∥AB,
∵四边形ABCD为平行四边形,
∴OC=OA,
∴CE=BE,
∴OE为△ABC的中位线,
∴OE= AB= ×8=4.
故答案为4.
【分析】利用作法得到∠COE=∠OAB,则OE//AB,利用平行四边形的性质判断OE为△A BC的中位线,从而得到OE的长.
15.【答案】①②④.
【解析】【解答】①∵F是AD的中点,
∴AF=FD,
∵在 ABCD中,AD=2AB,
∴AF=FD=CD,
∴∠DFC=∠DCF,
∵AD∥BC,
∴∠DFC=∠FCB,
∴∠DCF=∠BCF,
∴∠DCF= ∠BCD,故此选项正确;
延长EF,交CD延长线于M,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠A=∠MDF,
∵F为AD中点,
∴AF=FD,
在△AEF和△DFM中,
,
∴△AEF≌△DMF(ASA),
∴FE=MF,∠AEF=∠M,
∵CE⊥AB,
∴∠AEC=90°,
∴∠AEC=∠ECD=90°,
∵FM=EF,
∴FC=FM,故②正确;
③∵EF=FM,
∴S△EFC=S△CFM,
∵MC>BE,
∴S△BEC<2S△EFC
故S△BEC=2S△CEF错误;
④设∠FEC=x,则∠FCE=x,
∴∠DCF=∠DFC=90°-x,
∴∠EFC=180°-2x,
∴∠EFD=90°-x+180°-2x=270°-3x,
∵∠AEF=90°-x,
∴∠DFE=3∠AEF,故此选项正确.
16.【答案】4
【解析】【解答】解:∵四边形ABCD是平行四边形,
∴AD∥BC,BC=AD=3cm,
若以P,D,Q,B四点组成的四边形是平行四边形,则PD=BQ,
设运动时间为t秒,当点Q从C到B过程中,
则AP=0.5t,CQ=t,PD=3-0.5t,BQ=3-t,
∴3-0.5t=3-t,
解得:t=0,不合题意;
当点P到达B返回过程中,PD=3-0.5t,BQ=t-3,
∴3-0.5t=t-3,
解得:t=4,
∴当运动时间为4时,以P,D,Q,B四点组成的四边形是平行四边形 ;
故答案为:4.
【分析】由PD∥BQ,可知以P,D,Q,B四点组成的四边形是平行四边形时,则PD=BQ,设运动时间为t秒,分两种情况:当点Q从C到B过程中和当点P到达B返回过程中,据此分别列出方程并求解即可.
17.【答案】解:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴∠ADB=∠DBC,
∵∠ADF+∠ADB=180°,∠CBE+∠DBC=180°,
∴∠ADF=∠CBE,
∵DF=BE,
∴△ADF≌△CBE,
∴AF=CE.
【解析】【分析】根据平行四边形的性质得出 AD∥BC,AD=BC, 根据二直线平行,内错角相等得出 ∠ADB=∠DBC, 进而根据等角的补角相等得出 ∠ADF=∠CBE, 从而利用SAS判断出 △ADF≌△CBE, 根据全等三角形的对应边相等得出 AF=CE.
18.【答案】证明:∵四边形ABCD是平行四边形,∴OA=OC,AB∥CD 。∴∠OAE=∠OCF 。∵∠AOE=∠COF ,∴△OAE≌△OCF(ASA)。∴OE=OF。
【解析】【分析】根据平行四边形的性质得出OA=OC,AB∥CD ,可证得∠OAE=∠OCF,再利用ASA证明△OAE≌△OCF,然后利用全等三角形的性质即可证得结论。
19.【答案】证明:连接AF,CE,
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵BE=DF,
∴AB﹣BE=CD﹣DF,
∴AE=CF,
∴四边形AECF是平行四边形,
∴PA=PC.
【解析】【分析】首先连接AF,CE,由四边形ABCD是平行四边形,可得AB∥CD,AB=CD,又由BE=DF,证得AE=CF,即可证得四边形AECF是平行四边形,继而证得结论.
20.【答案】证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴∠1=∠2,
∵BF=DE,
∴BF+BD=DE+BD,
即DF=BE,
在△ADF和△CBE中,
,
∴△ADF≌△CBE(SAS),
∴∠AFD=∠CEB,
∴AF∥CE.
【解析】【分析】由平行四边形的性质得出AD∥BC,AD=BC,证出∠1=∠2,DF=BE,由SAS证明△ADF≌△CBE,得出对应角相等,再由平行线的判定即可得出结论.本题考查了平行四边形的性质,全等三角形的判定与性质、平行线的性质;熟练掌握平行四边形的性质,证明三角形全等是解决问题的关键.
21.【答案】证明:∵四边形ABCD是平行四边形ABCD,
∴OA=OC,DF∥EB
∴∠E=∠F
又∵∠EOA=∠FOC
∴△OAE≌△OCF,∴OE=OF
【解析】【分析】本题考查平行四边形的性质.掌握平行四边形对边相等、对角线互相平分的性质,同时结合此前学过的证明线段相等的方法,就能解答本题
22.【答案】6
【解析】【解答】解 :如图,取BC的中点G,连接DG、EG、FG.
∵ AD∶BC=1∶2 ;G是BC的中点,
∴ BG=AD ;
又∵AD//BC ;
∴四边形ABGD是平行四边形;
∴S△ADE+S△BEG=S平行四边形ABDG
S△AFD+S△BG=S平行四边形ABDG
∴上面两个三角形的面积差与下面两个三角形面积差相等。
∵上面两个三角形面积差相当于图中△OAF和△ODE的面积之差,是△AOF的2倍。
下面两个三角形面积差是(S△BEC+24)÷2 S△BEC÷2=12
∴S△AOF=12÷2=6m2.
【分析】如图,取BC的中点G,连接DG、EG、FG.根据一组对边平行且相等的四边形是平行四边形得出四边形ABGD是平行四边形; 根据平行四边形的面积公式,三角形的面积计算公式得出S△ADE+S△BEG=S平行四边形ABDG,S△AFD+S△BG=S平行四边形ABDG;从而得出上面两个三角形的面积差与下面两个三角形面积差相等;进而得出上面两个三角形面积差相当于图中△OAF和△ODE的面积之差,是△AOF的2倍;下面两个三角形面积差是(S△BEC+24)÷2 S△BEC÷2=12;从而得出答案。
1 / 1
