沪教版八年级数学下册 期末模拟卷(含解析)
文档属性
| 名称 | 沪教版八年级数学下册 期末模拟卷(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 170.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-05 10:28:52 | ||
图片预览



文档简介
期末模拟卷
一、选择题(本大题共6小题,每小题2分,共12分)
1.下列关于向量的运算中,正确的是( )
A. B.
C. D.
2.若﹣=0有增根,则m的值是( )
A.3 B.2 C.﹣3 D.﹣2
3.下列事件:①上海明天是晴天,②铅球浮在水面上,③平面中,多边形的外角和都等于360度,属于确定事件的个数有( )
A.0个 B.1个 C.2个 D.3个
4.如图,五边形ABCDE是正五边形,则x为( )
A.30° B.35° C.36° D.45°
5.如图,已知一次函数y=kx+b的图象经过A、B两点,那么不等式kx+b>0的解集是( )
A.x>3 B.x<3 C.x>5 D.x<5
6.如图,在 ABCD中,DE平分∠ADC,AD=6,BE=2,则 ABCD的周长是( )
A.60 B.30 C.20 D.16
二、填空题(本大题共12小题,每小题2分,共24分.不需写出解答过程,请把答案直接填写在横线上)
7.方程x3+8=0的根是 .
8.关于x的方程a2x+x=1的解是 .
9.已知直线y=kx+b经过点(﹣2,2),并且与直线y=2x+1平行,那么b= .
10.已知关于x的方程+=,如果设=y,那么原方程化为关于y的方程是 .
11.方程的解为 .
12.2名男生和2名女生抓阄分派2张电影票,恰好2名女生得到电影票的概率是 .
13.如果多边形的每个外角都是40°,那么这个多边形的边数是 .
14.在 ABCD中,对角线AC和BD交于点O,AB=2,AC=6,BD=8,那么△COD的周长为 .
15.已知菱形的边长为6cm,一个角为60°,那么菱形的面积为 cm2.
16.一个矩形在直角坐标平面上的三个顶点的坐标分别是(﹣2,﹣1)、(3,﹣1)、(﹣2,3),那么第四个顶点的坐标是 .
17.如图,平行四边形ABCD中,∠B=60°,AB=8cm,AD=10cm,点P在边BC上从B向C运动,点Q在边DA上从D向A运动,如果P,Q运动的速度都为每秒1cm,那么当运动时间t= 秒时,四边形ABPQ是直角梯形.
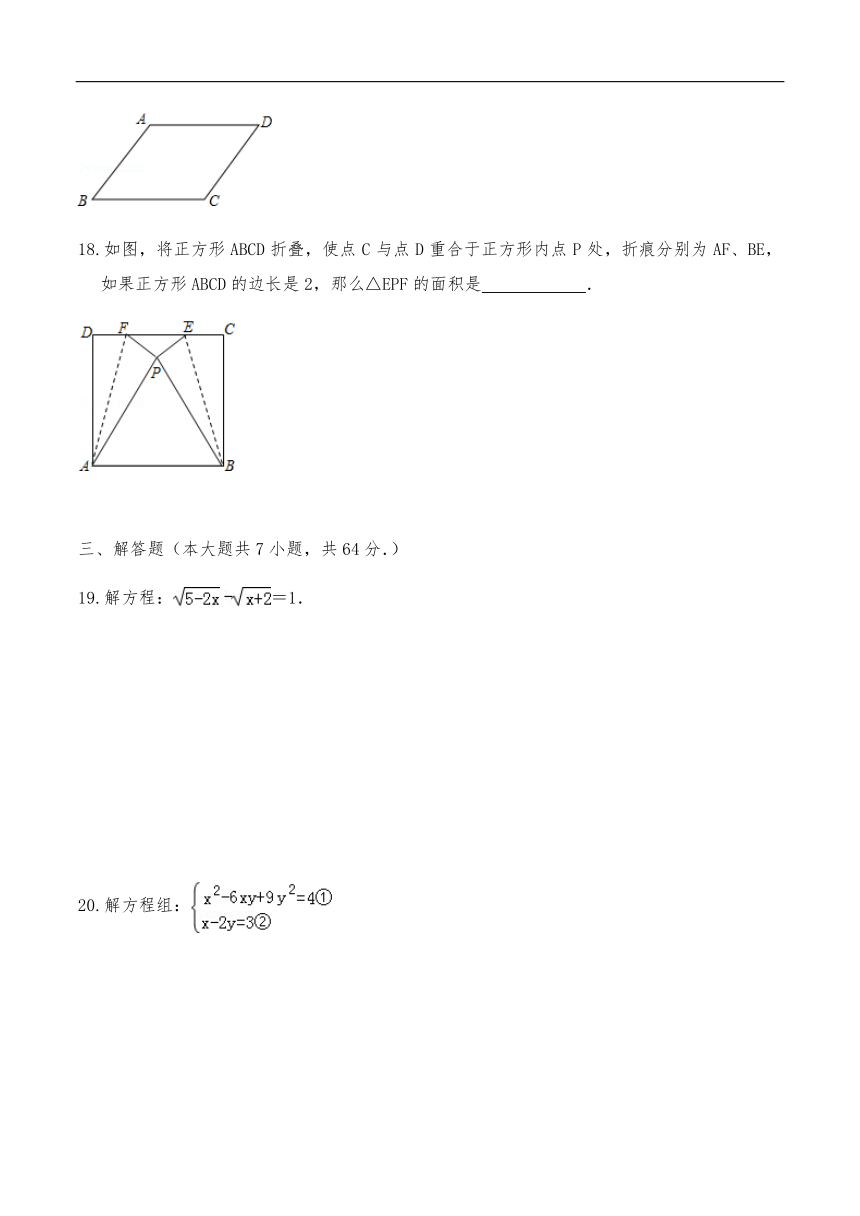
18.如图,将正方形ABCD折叠,使点C与点D重合于正方形内点P处,折痕分别为AF、BE,如果正方形ABCD的边长是2,那么△EPF的面积是 .
三、解答题(本大题共7小题,共64分.)
19.解方程:=1.
20.解方程组:
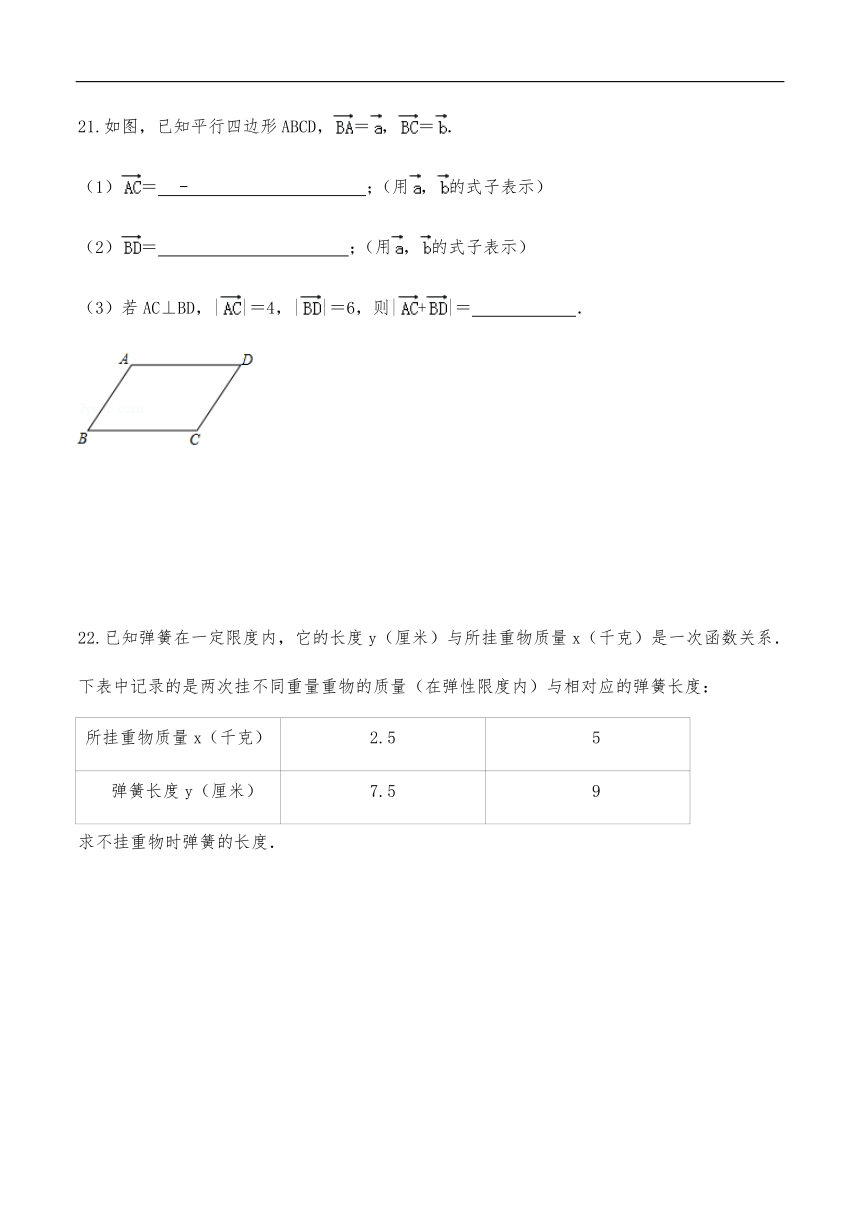
21.如图,已知平行四边形ABCD,=,=.
(1)= ﹣ ;(用,的式子表示)
(2)= ;(用,的式子表示)
(3)若AC⊥BD,||=4,||=6,则|+|= .
22.已知弹簧在一定限度内,它的长度y(厘米)与所挂重物质量x(千克)是一次函数关系.
下表中记录的是两次挂不同重量重物的质量(在弹性限度内)与相对应的弹簧长度:
所挂重物质量x(千克) 2.5 5
弹簧长度y(厘米) 7.5 9
求不挂重物时弹簧的长度.
23.如图,△ABC中,AD是边BC上的中线,过点A作AE∥BC,过点D作DE∥AB,DE与AC、AE分别交于点O、点E,连接EC.
(1)求证:AD=EC;
(2)当∠BAC=90°时,求证:四边形ADCE是菱形.
24.黄浦区政府为残疾人办实事,在道路改造工程中为盲人修建一条长3000米的盲道,根据规划设计和要求,某工程队在实际施工中增加了施工人员,每天修建的盲道比原计划多250米,结果提前2天完成工程,问实际每天修建盲道多少米.
25.如图,已知正方形ABCD的边长为3,菱形EFGH的三个顶点E、G、H分别在正方形的边AB、CD、DA上,AH=1,联结CF.
(1)当DG=1时,求证:菱形EFGH为正方形;
(2)设DG=x,△FCG的面积为y,写出y关于x的函数解析式,并指出x的取值范围;
(3)当DG=时,求∠GHE的度数.
答案
一、选择题
1.B
【解答】解:A、,故本选项错误.
B、,故本选项正确.
C、+(﹣)=,故本选项错误.
D、+=,故本选项错误.
故选:B.
2.A
【解答】解:去分母得m+1﹣x=0,
方程的增根为4,
把x=4代入m+1﹣x=0得m+1﹣4=0,解得m=3.
故选:A.
3.C
【解答】解:①上海明天是晴天,是随机事件;
②铅球浮在水面上,是不可能事件,属于确定事件;
③平面中,多边形的外角和都等于360度,是必然事件,属于确定事件;
故选:C.
4.C
【解答】解:因为五边形ABCDE是正五边形,
所以∠E=∠CDE==108°,AE=DE,
所以,
所以x=∠CDE﹣∠1﹣∠3=36°.
故选:C.
5.D
【解答】解:∵一次函数y=kx+b的图象经过A、B两点,
由图象可知:A(5,0),
根据图象当x<5时,y>0,
即:不等式kx+b>0的解集是x<5.
故选:D.
6.C
【解答】解:∵DE平分∠ADC,
∴∠ADE=∠CDE,
∵ ABCD中,AD∥BC,
∴∠ADE=∠CED,
∴∠CDE=∠CED,
∴CE=CD,
在 ABCD中,AD=6,BE=2,
∴AD=BC=6,
∴CE=BC﹣BE=6﹣2=4,
∴CD=AB=4,
∴ ABCD的周长=6+6+4+4=20.
故选:C.
二、填空题
7.x=-2
【解答】解:(法1)方程可变形为x3=﹣8,
因为(﹣2)3=﹣8,
所以方程的解为x=﹣2.
故答案为:x=﹣2
(法2)方程可变形为x3=﹣8,
所以x==﹣2.
故答案为:x=﹣2
8.解:方程合并得:(a2+1)x=1,
解得:x=,
故答案为:
9.6
【解答】解:∵直线y=kx+b与直线y=2x+1平行,
∴k=2,
把(﹣2,2)代入y=2x+b得2×(﹣2)+b=2,解得b=6.
故答案为6;
10.解:由=y,可得
∴原方程化为3y+=
故答案为:3y+=
11.3
【解答】解:两边平方得:2x+3=x2
∴x2﹣2x﹣3=0,
解方程得:x1=3,x2=﹣1,
检验:当x1=3时,方程的左边=右边,所以x1=3为原方程的解,
当x2=﹣1时,原方程的左边≠右边,所以x2=﹣1不是原方程的解.
故答案为3.
12.解:画树状图得:
∵共有12种等可能的结果,恰好2名女生得到电影票的有2种情况,
∴恰好2名女生得到电影票的概率是:=.
故答案为:.
13.9
【解答】解:多边形的边数是:=9,
故答案为:9.
14.9
【解答】解:∵四边形ABCD是平行四边形,
∴OC=OA=AC=3,OD=OB=BD=4,CD=AB=2,
∴△COD的周长=OC+OD+CD=3+4+2=9.
故答案为9.
15.解:如图,过点D作DE⊥AB于点E,∠A=60°,
∵菱形的边长是6cm,
∴AB=AD=6cm,
∵在Rt△ADE中,∠A=60°,
∴∠ADE=30°,
∴AE=AD=3cm,
∴DE==3cm,
∴该菱形的面积=AB DE=18cm2.
故答案为:18.
16.(3,3)
【解答】解:过(﹣2,3)、(3,﹣1)两点分别作x轴、y轴的平行线,
交点为(3,3),即为第四个顶点坐标.
故答案为:(3,3).
17.7
【解答】解:
∵四边形ABCD是平行四边形,
∴AD∥BC,
过点A作AE⊥BC于E,
∴当AE∥QP时,则四边形ABPQ是直角梯形,
∵∠B=60°,AB=8cm,
∴BE=4cm,
∵P,Q运动的速度都为每秒1cm,
∴AQ=10﹣t,AP=t,
∵BE=4,
∴EP=t﹣4,
∵AE⊥BC,AQ∥EP,AE∥QP,
∴QP⊥BC,AQ⊥AD,
∴四边形AEPQ是矩形,
∴AQ=EP,
即10﹣t=t﹣4,
解得t=7,
故答案为:7.
18.解:过P作PH⊥DC于H,交AB于G,如图,
则PG⊥AB,
∵四边形ABCD为正方形,
∴AD=AB=BC=DC=2;∠D=∠C=90°,
又∵将正方形ABCD折叠,使点C与点D重合于形内点P处,
∴PA=PB=2,∠FPA=∠EPB=90°,
∴△PAB为等边三角形,
∴∠APB=60°,PG=AB=,
∴∠EPF=120°,PH=HG﹣PG=2﹣,
∴∠HEP=30°,
∴HE=PH=(2﹣)=2﹣3,
∴EF=2HE=4﹣6,
∴△EPF的面积=FE PH=(2﹣)(4﹣6)
=7﹣12.
故答案为7﹣12.
三、解答题
19.解:移项得:=1+,
两边平方得:5﹣2x=1+x+2+2,
2﹣3x=2,
两边平方得:4﹣12x+9x2=4x+8,
9x2﹣16x﹣4=0,
解得:x=2或x=﹣,
经检验:x=2是增根,x=﹣是原方程的根,
所以原方程的根是x=﹣.
20.解:由①,得(x﹣3y)2=4,
∴x﹣3y=±2,
∴原方程组可转化为:或
解得或
所以原方程组的解为:或
21.解:(1)=+=﹣+;
(2)=+=+;
(3)∵AC⊥BD,||=4,||=6,
∴|+|=2.
故答案为﹣+,+,2
22.解:设长度y(厘米)与所挂重物质量x(千克)的一次函数关系式是:y=kx+b(k≠0)
将表格中数据分别代入为:,
解得:,
∴y=x+6,
当x=0时,y=6.
答:不挂重物时弹簧的长度为6厘米.
23.证明:(1)∵DE∥AB,AE∥BC,
∴四边形ABDE是平行四边形,
∴AE∥BD,且AE=BD
又∵AD是BC边的中线,
∴BD=CD,
∴AE=CD,
∵AE∥CD,
∴四边形ADCE是平行四边形,
∴AD=EC;
(2)∵∠BAC=90°,AD是斜边BC上的中线,
∴AD=BD=CD,
又∵四边形ADCE是平行四边形,
∴四边形ADCE是菱形.
24.解:设实际每天修建盲道x米,根据题意可得:
﹣=2,
解得:x1=﹣500(不合题意舍去),x2=750,
经检验x=750是原方程的根,
答:实际每天修建盲道750米.
25.解:(1)在正方形ABCD中,
∵AH=1,
∴DH=2.
又∵DG=1,
∴HG=
在△AHE和△DGH中,
∵∠A=∠D=90°,AH=DG=1,EH=HG=,
∴△AHE≌△DGH,
∴∠AHE=∠DGH.
∵∠DGH+∠DHG=90°,∠AHE+∠DHG=90°.
∴∠GHE=90°
所以菱形EFGH是正方形;
(2)如图1,过点F作FM⊥DC交DC所在直线于M,联结GE.
∵AB∥CD,
∴∠AEG=∠MGE.
∵HE∥GF,
∴∠HEG=∠FGE.
∴∠HEA=∠FGM,
在△AHE和△MFG中,
∵∠A=∠M=90°,EH=GF.
∴△AHE≌△MFG.
∴FM=HA=1.
即无论菱形EFGH如何变化,点F到直线CD的距离始终为定值1,
∴y=GC FM=(3﹣x)×1=﹣x+(0≤x≤);
(3)如图2,当DG=时,
在Rt△HDG中,DH=2,根据勾股定理得,GH==;
∴HE=GH=,
在Rt△AEH中,根据勾股定理得,AE==,
过点G作GN⊥AB于N,
∴EN=AE﹣DG=
在Rt△ENG中,根据勾股定理得,GE==
∴GH=HE=GE,
∴△GHE为等边三角形.
∴∠GHE=60°.
一、选择题(本大题共6小题,每小题2分,共12分)
1.下列关于向量的运算中,正确的是( )
A. B.
C. D.
2.若﹣=0有增根,则m的值是( )
A.3 B.2 C.﹣3 D.﹣2
3.下列事件:①上海明天是晴天,②铅球浮在水面上,③平面中,多边形的外角和都等于360度,属于确定事件的个数有( )
A.0个 B.1个 C.2个 D.3个
4.如图,五边形ABCDE是正五边形,则x为( )
A.30° B.35° C.36° D.45°
5.如图,已知一次函数y=kx+b的图象经过A、B两点,那么不等式kx+b>0的解集是( )
A.x>3 B.x<3 C.x>5 D.x<5
6.如图,在 ABCD中,DE平分∠ADC,AD=6,BE=2,则 ABCD的周长是( )
A.60 B.30 C.20 D.16
二、填空题(本大题共12小题,每小题2分,共24分.不需写出解答过程,请把答案直接填写在横线上)
7.方程x3+8=0的根是 .
8.关于x的方程a2x+x=1的解是 .
9.已知直线y=kx+b经过点(﹣2,2),并且与直线y=2x+1平行,那么b= .
10.已知关于x的方程+=,如果设=y,那么原方程化为关于y的方程是 .
11.方程的解为 .
12.2名男生和2名女生抓阄分派2张电影票,恰好2名女生得到电影票的概率是 .
13.如果多边形的每个外角都是40°,那么这个多边形的边数是 .
14.在 ABCD中,对角线AC和BD交于点O,AB=2,AC=6,BD=8,那么△COD的周长为 .
15.已知菱形的边长为6cm,一个角为60°,那么菱形的面积为 cm2.
16.一个矩形在直角坐标平面上的三个顶点的坐标分别是(﹣2,﹣1)、(3,﹣1)、(﹣2,3),那么第四个顶点的坐标是 .
17.如图,平行四边形ABCD中,∠B=60°,AB=8cm,AD=10cm,点P在边BC上从B向C运动,点Q在边DA上从D向A运动,如果P,Q运动的速度都为每秒1cm,那么当运动时间t= 秒时,四边形ABPQ是直角梯形.
18.如图,将正方形ABCD折叠,使点C与点D重合于正方形内点P处,折痕分别为AF、BE,如果正方形ABCD的边长是2,那么△EPF的面积是 .
三、解答题(本大题共7小题,共64分.)
19.解方程:=1.
20.解方程组:
21.如图,已知平行四边形ABCD,=,=.
(1)= ﹣ ;(用,的式子表示)
(2)= ;(用,的式子表示)
(3)若AC⊥BD,||=4,||=6,则|+|= .
22.已知弹簧在一定限度内,它的长度y(厘米)与所挂重物质量x(千克)是一次函数关系.
下表中记录的是两次挂不同重量重物的质量(在弹性限度内)与相对应的弹簧长度:
所挂重物质量x(千克) 2.5 5
弹簧长度y(厘米) 7.5 9
求不挂重物时弹簧的长度.
23.如图,△ABC中,AD是边BC上的中线,过点A作AE∥BC,过点D作DE∥AB,DE与AC、AE分别交于点O、点E,连接EC.
(1)求证:AD=EC;
(2)当∠BAC=90°时,求证:四边形ADCE是菱形.
24.黄浦区政府为残疾人办实事,在道路改造工程中为盲人修建一条长3000米的盲道,根据规划设计和要求,某工程队在实际施工中增加了施工人员,每天修建的盲道比原计划多250米,结果提前2天完成工程,问实际每天修建盲道多少米.
25.如图,已知正方形ABCD的边长为3,菱形EFGH的三个顶点E、G、H分别在正方形的边AB、CD、DA上,AH=1,联结CF.
(1)当DG=1时,求证:菱形EFGH为正方形;
(2)设DG=x,△FCG的面积为y,写出y关于x的函数解析式,并指出x的取值范围;
(3)当DG=时,求∠GHE的度数.
答案
一、选择题
1.B
【解答】解:A、,故本选项错误.
B、,故本选项正确.
C、+(﹣)=,故本选项错误.
D、+=,故本选项错误.
故选:B.
2.A
【解答】解:去分母得m+1﹣x=0,
方程的增根为4,
把x=4代入m+1﹣x=0得m+1﹣4=0,解得m=3.
故选:A.
3.C
【解答】解:①上海明天是晴天,是随机事件;
②铅球浮在水面上,是不可能事件,属于确定事件;
③平面中,多边形的外角和都等于360度,是必然事件,属于确定事件;
故选:C.
4.C
【解答】解:因为五边形ABCDE是正五边形,
所以∠E=∠CDE==108°,AE=DE,
所以,
所以x=∠CDE﹣∠1﹣∠3=36°.
故选:C.
5.D
【解答】解:∵一次函数y=kx+b的图象经过A、B两点,
由图象可知:A(5,0),
根据图象当x<5时,y>0,
即:不等式kx+b>0的解集是x<5.
故选:D.
6.C
【解答】解:∵DE平分∠ADC,
∴∠ADE=∠CDE,
∵ ABCD中,AD∥BC,
∴∠ADE=∠CED,
∴∠CDE=∠CED,
∴CE=CD,
在 ABCD中,AD=6,BE=2,
∴AD=BC=6,
∴CE=BC﹣BE=6﹣2=4,
∴CD=AB=4,
∴ ABCD的周长=6+6+4+4=20.
故选:C.
二、填空题
7.x=-2
【解答】解:(法1)方程可变形为x3=﹣8,
因为(﹣2)3=﹣8,
所以方程的解为x=﹣2.
故答案为:x=﹣2
(法2)方程可变形为x3=﹣8,
所以x==﹣2.
故答案为:x=﹣2
8.解:方程合并得:(a2+1)x=1,
解得:x=,
故答案为:
9.6
【解答】解:∵直线y=kx+b与直线y=2x+1平行,
∴k=2,
把(﹣2,2)代入y=2x+b得2×(﹣2)+b=2,解得b=6.
故答案为6;
10.解:由=y,可得
∴原方程化为3y+=
故答案为:3y+=
11.3
【解答】解:两边平方得:2x+3=x2
∴x2﹣2x﹣3=0,
解方程得:x1=3,x2=﹣1,
检验:当x1=3时,方程的左边=右边,所以x1=3为原方程的解,
当x2=﹣1时,原方程的左边≠右边,所以x2=﹣1不是原方程的解.
故答案为3.
12.解:画树状图得:
∵共有12种等可能的结果,恰好2名女生得到电影票的有2种情况,
∴恰好2名女生得到电影票的概率是:=.
故答案为:.
13.9
【解答】解:多边形的边数是:=9,
故答案为:9.
14.9
【解答】解:∵四边形ABCD是平行四边形,
∴OC=OA=AC=3,OD=OB=BD=4,CD=AB=2,
∴△COD的周长=OC+OD+CD=3+4+2=9.
故答案为9.
15.解:如图,过点D作DE⊥AB于点E,∠A=60°,
∵菱形的边长是6cm,
∴AB=AD=6cm,
∵在Rt△ADE中,∠A=60°,
∴∠ADE=30°,
∴AE=AD=3cm,
∴DE==3cm,
∴该菱形的面积=AB DE=18cm2.
故答案为:18.
16.(3,3)
【解答】解:过(﹣2,3)、(3,﹣1)两点分别作x轴、y轴的平行线,
交点为(3,3),即为第四个顶点坐标.
故答案为:(3,3).
17.7
【解答】解:
∵四边形ABCD是平行四边形,
∴AD∥BC,
过点A作AE⊥BC于E,
∴当AE∥QP时,则四边形ABPQ是直角梯形,
∵∠B=60°,AB=8cm,
∴BE=4cm,
∵P,Q运动的速度都为每秒1cm,
∴AQ=10﹣t,AP=t,
∵BE=4,
∴EP=t﹣4,
∵AE⊥BC,AQ∥EP,AE∥QP,
∴QP⊥BC,AQ⊥AD,
∴四边形AEPQ是矩形,
∴AQ=EP,
即10﹣t=t﹣4,
解得t=7,
故答案为:7.
18.解:过P作PH⊥DC于H,交AB于G,如图,
则PG⊥AB,
∵四边形ABCD为正方形,
∴AD=AB=BC=DC=2;∠D=∠C=90°,
又∵将正方形ABCD折叠,使点C与点D重合于形内点P处,
∴PA=PB=2,∠FPA=∠EPB=90°,
∴△PAB为等边三角形,
∴∠APB=60°,PG=AB=,
∴∠EPF=120°,PH=HG﹣PG=2﹣,
∴∠HEP=30°,
∴HE=PH=(2﹣)=2﹣3,
∴EF=2HE=4﹣6,
∴△EPF的面积=FE PH=(2﹣)(4﹣6)
=7﹣12.
故答案为7﹣12.
三、解答题
19.解:移项得:=1+,
两边平方得:5﹣2x=1+x+2+2,
2﹣3x=2,
两边平方得:4﹣12x+9x2=4x+8,
9x2﹣16x﹣4=0,
解得:x=2或x=﹣,
经检验:x=2是增根,x=﹣是原方程的根,
所以原方程的根是x=﹣.
20.解:由①,得(x﹣3y)2=4,
∴x﹣3y=±2,
∴原方程组可转化为:或
解得或
所以原方程组的解为:或
21.解:(1)=+=﹣+;
(2)=+=+;
(3)∵AC⊥BD,||=4,||=6,
∴|+|=2.
故答案为﹣+,+,2
22.解:设长度y(厘米)与所挂重物质量x(千克)的一次函数关系式是:y=kx+b(k≠0)
将表格中数据分别代入为:,
解得:,
∴y=x+6,
当x=0时,y=6.
答:不挂重物时弹簧的长度为6厘米.
23.证明:(1)∵DE∥AB,AE∥BC,
∴四边形ABDE是平行四边形,
∴AE∥BD,且AE=BD
又∵AD是BC边的中线,
∴BD=CD,
∴AE=CD,
∵AE∥CD,
∴四边形ADCE是平行四边形,
∴AD=EC;
(2)∵∠BAC=90°,AD是斜边BC上的中线,
∴AD=BD=CD,
又∵四边形ADCE是平行四边形,
∴四边形ADCE是菱形.
24.解:设实际每天修建盲道x米,根据题意可得:
﹣=2,
解得:x1=﹣500(不合题意舍去),x2=750,
经检验x=750是原方程的根,
答:实际每天修建盲道750米.
25.解:(1)在正方形ABCD中,
∵AH=1,
∴DH=2.
又∵DG=1,
∴HG=
在△AHE和△DGH中,
∵∠A=∠D=90°,AH=DG=1,EH=HG=,
∴△AHE≌△DGH,
∴∠AHE=∠DGH.
∵∠DGH+∠DHG=90°,∠AHE+∠DHG=90°.
∴∠GHE=90°
所以菱形EFGH是正方形;
(2)如图1,过点F作FM⊥DC交DC所在直线于M,联结GE.
∵AB∥CD,
∴∠AEG=∠MGE.
∵HE∥GF,
∴∠HEG=∠FGE.
∴∠HEA=∠FGM,
在△AHE和△MFG中,
∵∠A=∠M=90°,EH=GF.
∴△AHE≌△MFG.
∴FM=HA=1.
即无论菱形EFGH如何变化,点F到直线CD的距离始终为定值1,
∴y=GC FM=(3﹣x)×1=﹣x+(0≤x≤);
(3)如图2,当DG=时,
在Rt△HDG中,DH=2,根据勾股定理得,GH==;
∴HE=GH=,
在Rt△AEH中,根据勾股定理得,AE==,
过点G作GN⊥AB于N,
∴EN=AE﹣DG=
在Rt△ENG中,根据勾股定理得,GE==
∴GH=HE=GE,
∴△GHE为等边三角形.
∴∠GHE=60°.
同课章节目录
