初中数学沪科版八年级上册1.3.2三角形内角和定理教学设计(含答案)
文档属性
| 名称 | 初中数学沪科版八年级上册1.3.2三角形内角和定理教学设计(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 103.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-05 11:02:52 | ||
图片预览


文档简介
教学设计
课程基本信息
学科 数学 年级 八年级 学期 秋季
课题 命题与证明:三角形内角和定理
教科书 书 名:义务教育教科书数学八年级上册 出版社:上海科学技术出版社 出版日期:2013年6月
教学目标
1.理解三角形内角和定理,在参与观察、实验、折纸、剪纸等数学活动中,体会思维实验和理性推理的作用,清晰地表达自己的想法。 2.掌握三角形内角和定理的证明和简单应用,初步学会作辅助线证明的基本方法。 3.运用三角形内角和定理解决简单的问题。获得分析问题和解决问题的一些基本方法,体验证明定理方法的多样性,发展创新意识。 4.学生积极参与数学活动,对数学有好奇心和求知欲。在分组展示中体验成功的乐趣,建立自信心。
教学内容
教学重点: 1.在动手实践过程中会寻找证明三角形内角和定理的路径、思考多种证明方法的本质联系。
2. 能够根据不同方法在证明中添加合适的辅助线,感受辅助线的必要性。
教学难点: 1.学会利用三角形内角和定理进行几何计算。
2.学会利用三角形内角和定理解决实际生活问题。
教学过程
教学环节所用时间教学过程课前准备学生准备三角形纸片、直尺、剪刀、量角器等工具;布置复习作业:平角的定义、平行线的性质 引入与操作 3分钟引入:三角形是我们从小学到初中一直在学习,一直在应用的一个几何基本图形,三角形在生活中也随处可见,比如交通标识、热带鱼、三角蛋糕以及金字塔等等,三角形已经成为我们生活中最常见的图形之一,可见三角形对我们的生活、学习有多重要。 问题1:在小学我们就学习过了三角形的三个内角之和为180°,那大家还记得我们在小学是怎样验证这个结论的吗?请大家利用手中的三角形纸片进行探究.
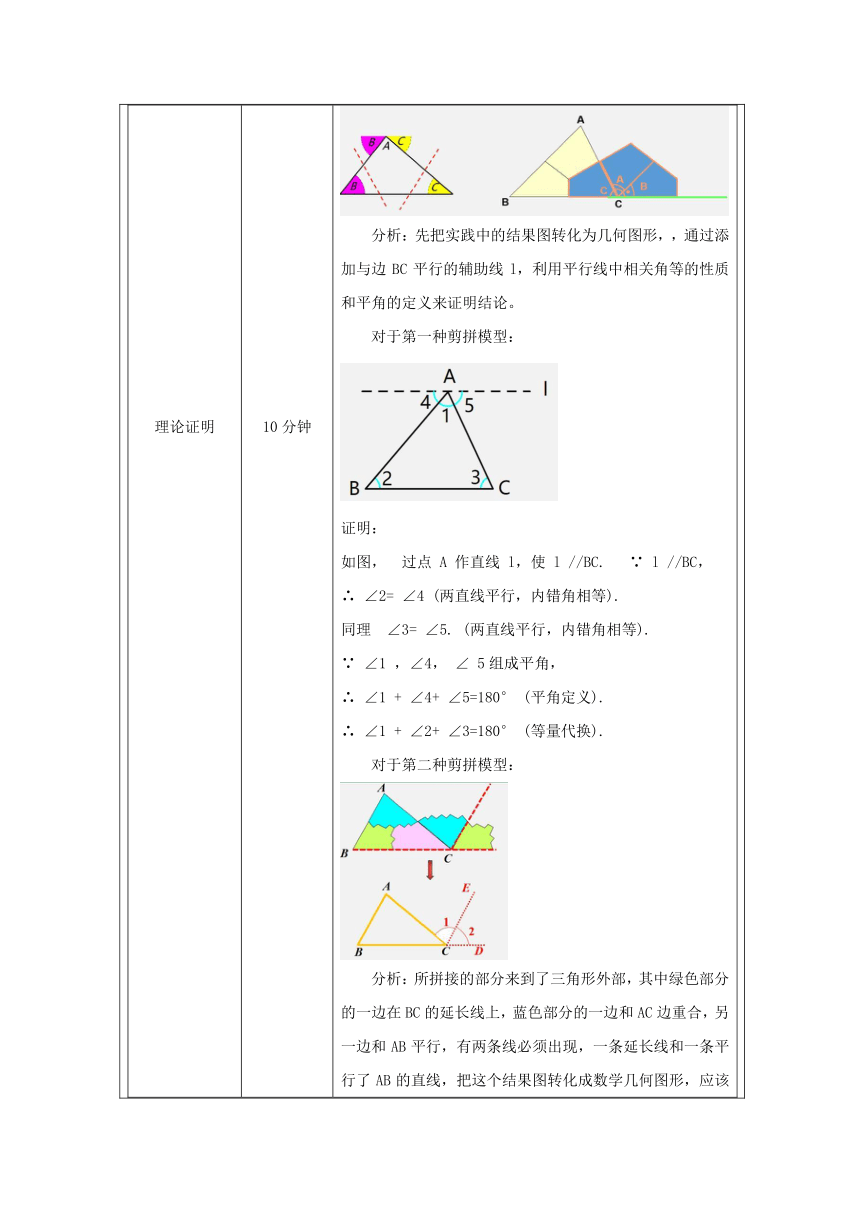
有的同学利用量角器度量一个三角形的三个内角的度数,计算这三个内角的和. 但是,在度量的过程中,往往会有误差;有的同学采用折叠的方法,将各角沿着一边所在的直线折叠;有的同学如下图通过剪图、拼图的方法得出结论。 大家通过自己动手实践验证了自己手中的三角形内角和是180°,形状不同的、大小不同的三角形有无数个,那我们能不能把通过剪拼或折叠把所有三角形都验证一遍,显然不行,那基于刚才的实践,我们能不能找适合的方法、用严谨的的证明来验证所有三角形的内角和都等于180°呢? 分析:用数学语言来翻译,验证对象是三角形,所以我们应该先任意画一个三角形,把文字叙述翻译为了几何图形直观叙述,其次要验证的是三个内角之和,也就是∠A+∠B+∠C=180°在 ABC,∠A+∠B+∠C=180° 理论证明 10分钟问题2:拼接实验,∠B 和∠C 分别拼在∠A 的左右,三个角合起来形成一个平角,发现了一条过点A 平行与边BC的直线l,从平行线的性质入手,大家能给出三角形内角和为180°的严谨证明吗? 分析:先把实践中的结果图转化为几何图形,,通过添加与边BC平行的辅助线l,利用平行线中相关角等的性质和平角的定义来证明结论。 对于第一种剪拼模型: 证明: 如图, 过点 A 作直线 l,使 l //BC. ∵ l //BC, ∴ ∠2= ∠4 (两直线平行,内错角相等). 同理 ∠3= ∠5. (两直线平行,内错角相等). ∵ ∠1 ,∠4, ∠ 5组成平角, ∴ ∠1 + ∠4+ ∠5=180° (平角定义). ∴ ∠1 + ∠2+ ∠3=180° (等量代换). 对于第二种剪拼模型: 分析:所拼接的部分来到了三角形外部,其中绿色部分的一边在BC的延长线上,蓝色部分的一边和AC边重合,另一边和AB平行,有两条线必须出现,一条延长线和一条平行了AB的直线,把这个结果图转化成数学几何图形,应该先是一个三角形,在三角形的基础之上,延长BC,过点C做AB的平行线CE. 证明: 延长BC到D,过点C作CE//BA, ∴ ∠A=∠1 ,(两直线平行,内错角相等) ∠B=∠2.(两直线平行,同位角相等) 又∵∠1+∠2+∠ACB=180°.(平角定义) ∴∠A+∠B+∠ACB=180°.(等量代换) 总结结论: 三角形内角和定理:三角形的内角和等于180° 符号语言:在△ABC 中,∠A +∠B +∠C=180° 应用新知 5分钟解决以下问题,以下度数能否组成三角形: 3°, 150°, 27° ; 60°, 40°, 90° 答案:能、不能 答案:100° 已知△ABC是直角三角形,∠B=90°,则∠A+∠C=( ) A.90° B.80° C.110° D.45° 分析:∵在△ABC中,有∠A +∠B +∠C=180°,且∠B=90°, ∴ ∠A+∠C=180°- ∠B= 180°- 90°=90° 3.在△ABC中,∠ B+∠ C=90°,则△ABC是一个( ) A.锐角三角形 B.直角三角形 C.钝角三角形 D.不能确定 分析: ∵在△ABC中,有∠A +∠B +∠C=180°,且∠B+∠C=90° ∴ ∠A=180°- (∠B +∠C )= 180°- 90°=90° 归纳总结:可以利用三角形内角和定理解决: (1)判断三个角能否是某个三角形的三个内角 (2)已知两角计算第三个角、判断直角三角形 (3)生活中的实际问题 4.图是A,B,C三岛的平面图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80°方向,C岛在B岛的北偏西40°方向。求∠ABC和∠ACB的度数? 分析:首先将题目中的方位角标出如下图: A,B,C三岛的连线构成△ABC,所求的∠ABC和∠ ACB是△ABC的两个内角。 ∠ABC可以通过平行线知识求出,如果能求出∠CAB,就能求出∠ACB的度数 解:由题知: ∠CAD=50°,∠BAD=80°,∠EBC=40° ∴ ∠CAB=∠BAD -∠CAD=80°-50°=30° ∵ AD//BE ∴ ∠BAD+∠ ABE=180° ∴ ∠ABE=180°-∠BAD = 180°- 80°= 100° ∴ ∠ABC=∠ABE -∠EBC=100°-40°=60° ∴ 在△ABC中,∠ACB =180°-∠ABC-∠ CAB =180°-60°-30°=90°. 综上: ∠ABC=60°, ∠ACB=90° 课堂小结 2分钟1.本节课主要学习了什么知识?学习到了什么新的方法? 2.思考为什么需要对三角形内角和定理进行严谨证明? 3.思考:在△ABC中除了三个内角的关系外,你还能探索出其他的角吗?这些角又有什么关系呢?
课程基本信息
学科 数学 年级 八年级 学期 秋季
课题 命题与证明:三角形内角和定理
教科书 书 名:义务教育教科书数学八年级上册 出版社:上海科学技术出版社 出版日期:2013年6月
教学目标
1.理解三角形内角和定理,在参与观察、实验、折纸、剪纸等数学活动中,体会思维实验和理性推理的作用,清晰地表达自己的想法。 2.掌握三角形内角和定理的证明和简单应用,初步学会作辅助线证明的基本方法。 3.运用三角形内角和定理解决简单的问题。获得分析问题和解决问题的一些基本方法,体验证明定理方法的多样性,发展创新意识。 4.学生积极参与数学活动,对数学有好奇心和求知欲。在分组展示中体验成功的乐趣,建立自信心。
教学内容
教学重点: 1.在动手实践过程中会寻找证明三角形内角和定理的路径、思考多种证明方法的本质联系。
2. 能够根据不同方法在证明中添加合适的辅助线,感受辅助线的必要性。
教学难点: 1.学会利用三角形内角和定理进行几何计算。
2.学会利用三角形内角和定理解决实际生活问题。
教学过程
教学环节所用时间教学过程课前准备学生准备三角形纸片、直尺、剪刀、量角器等工具;布置复习作业:平角的定义、平行线的性质 引入与操作 3分钟引入:三角形是我们从小学到初中一直在学习,一直在应用的一个几何基本图形,三角形在生活中也随处可见,比如交通标识、热带鱼、三角蛋糕以及金字塔等等,三角形已经成为我们生活中最常见的图形之一,可见三角形对我们的生活、学习有多重要。 问题1:在小学我们就学习过了三角形的三个内角之和为180°,那大家还记得我们在小学是怎样验证这个结论的吗?请大家利用手中的三角形纸片进行探究.
有的同学利用量角器度量一个三角形的三个内角的度数,计算这三个内角的和. 但是,在度量的过程中,往往会有误差;有的同学采用折叠的方法,将各角沿着一边所在的直线折叠;有的同学如下图通过剪图、拼图的方法得出结论。 大家通过自己动手实践验证了自己手中的三角形内角和是180°,形状不同的、大小不同的三角形有无数个,那我们能不能把通过剪拼或折叠把所有三角形都验证一遍,显然不行,那基于刚才的实践,我们能不能找适合的方法、用严谨的的证明来验证所有三角形的内角和都等于180°呢? 分析:用数学语言来翻译,验证对象是三角形,所以我们应该先任意画一个三角形,把文字叙述翻译为了几何图形直观叙述,其次要验证的是三个内角之和,也就是∠A+∠B+∠C=180°在 ABC,∠A+∠B+∠C=180° 理论证明 10分钟问题2:拼接实验,∠B 和∠C 分别拼在∠A 的左右,三个角合起来形成一个平角,发现了一条过点A 平行与边BC的直线l,从平行线的性质入手,大家能给出三角形内角和为180°的严谨证明吗? 分析:先把实践中的结果图转化为几何图形,,通过添加与边BC平行的辅助线l,利用平行线中相关角等的性质和平角的定义来证明结论。 对于第一种剪拼模型: 证明: 如图, 过点 A 作直线 l,使 l //BC. ∵ l //BC, ∴ ∠2= ∠4 (两直线平行,内错角相等). 同理 ∠3= ∠5. (两直线平行,内错角相等). ∵ ∠1 ,∠4, ∠ 5组成平角, ∴ ∠1 + ∠4+ ∠5=180° (平角定义). ∴ ∠1 + ∠2+ ∠3=180° (等量代换). 对于第二种剪拼模型: 分析:所拼接的部分来到了三角形外部,其中绿色部分的一边在BC的延长线上,蓝色部分的一边和AC边重合,另一边和AB平行,有两条线必须出现,一条延长线和一条平行了AB的直线,把这个结果图转化成数学几何图形,应该先是一个三角形,在三角形的基础之上,延长BC,过点C做AB的平行线CE. 证明: 延长BC到D,过点C作CE//BA, ∴ ∠A=∠1 ,(两直线平行,内错角相等) ∠B=∠2.(两直线平行,同位角相等) 又∵∠1+∠2+∠ACB=180°.(平角定义) ∴∠A+∠B+∠ACB=180°.(等量代换) 总结结论: 三角形内角和定理:三角形的内角和等于180° 符号语言:在△ABC 中,∠A +∠B +∠C=180° 应用新知 5分钟解决以下问题,以下度数能否组成三角形: 3°, 150°, 27° ; 60°, 40°, 90° 答案:能、不能 答案:100° 已知△ABC是直角三角形,∠B=90°,则∠A+∠C=( ) A.90° B.80° C.110° D.45° 分析:∵在△ABC中,有∠A +∠B +∠C=180°,且∠B=90°, ∴ ∠A+∠C=180°- ∠B= 180°- 90°=90° 3.在△ABC中,∠ B+∠ C=90°,则△ABC是一个( ) A.锐角三角形 B.直角三角形 C.钝角三角形 D.不能确定 分析: ∵在△ABC中,有∠A +∠B +∠C=180°,且∠B+∠C=90° ∴ ∠A=180°- (∠B +∠C )= 180°- 90°=90° 归纳总结:可以利用三角形内角和定理解决: (1)判断三个角能否是某个三角形的三个内角 (2)已知两角计算第三个角、判断直角三角形 (3)生活中的实际问题 4.图是A,B,C三岛的平面图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80°方向,C岛在B岛的北偏西40°方向。求∠ABC和∠ACB的度数? 分析:首先将题目中的方位角标出如下图: A,B,C三岛的连线构成△ABC,所求的∠ABC和∠ ACB是△ABC的两个内角。 ∠ABC可以通过平行线知识求出,如果能求出∠CAB,就能求出∠ACB的度数 解:由题知: ∠CAD=50°,∠BAD=80°,∠EBC=40° ∴ ∠CAB=∠BAD -∠CAD=80°-50°=30° ∵ AD//BE ∴ ∠BAD+∠ ABE=180° ∴ ∠ABE=180°-∠BAD = 180°- 80°= 100° ∴ ∠ABC=∠ABE -∠EBC=100°-40°=60° ∴ 在△ABC中,∠ACB =180°-∠ABC-∠ CAB =180°-60°-30°=90°. 综上: ∠ABC=60°, ∠ACB=90° 课堂小结 2分钟1.本节课主要学习了什么知识?学习到了什么新的方法? 2.思考为什么需要对三角形内角和定理进行严谨证明? 3.思考:在△ABC中除了三个内角的关系外,你还能探索出其他的角吗?这些角又有什么关系呢?
