初中数学北师大版八年级下册6.3构造三角形中位线的常用方法习题课件(23张PPT)
文档属性
| 名称 | 初中数学北师大版八年级下册6.3构造三角形中位线的常用方法习题课件(23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-05 00:00:00 | ||
图片预览







文档简介
(共23张PPT)
微专题
构造三角形中位线的常用方法
北师版 八年级下
例
典 例 剖 析
证明:如图,延长AM,AN分别交BC于点F,G.
∵BD平分∠ABC,AN⊥BD,
∴∠ABN=∠GBN,∠ANB=∠GNB=90°.
又∵BN=BN,
∴△ABN≌△GBN(ASA).
∴AN=NG,AB=BG.
方法 1 连接两点构造三角形的中位线
分 类 训 练
1 [2023·成都外国语学校模拟]如图,在 ABCD中,对角线AC,BD相交于点O,∠BCD的平分线交边AB于点E,BF⊥CE于点F.
(1)求证:CF=EF;
(2)连接OF,若CD=9,AD=6,求OF的长.
(1)求证:CF=EF;
【证明】在 ABCD中,AB与CD平行,
∴∠DCE=∠BEC.
∵CE平分∠BCD,∴∠DCE=∠BCE,
∴∠BEC=∠BCE,∴BC=BE.
∵BF⊥CE,∴CF=EF.
(2)连接OF,若CD=9,AD=6,求OF的长.
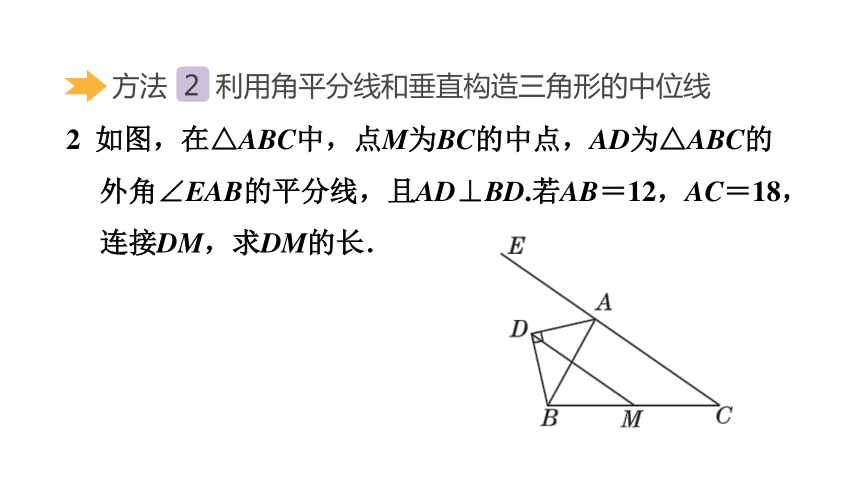
2 如图,在△ABC中,点M为BC的中点,AD为△ABC的外角∠EAB的平分线,且AD⊥BD.若AB=12,AC=18,连接DM,求DM的长.
方法 2 利用角平分线和垂直构造三角形的中位线
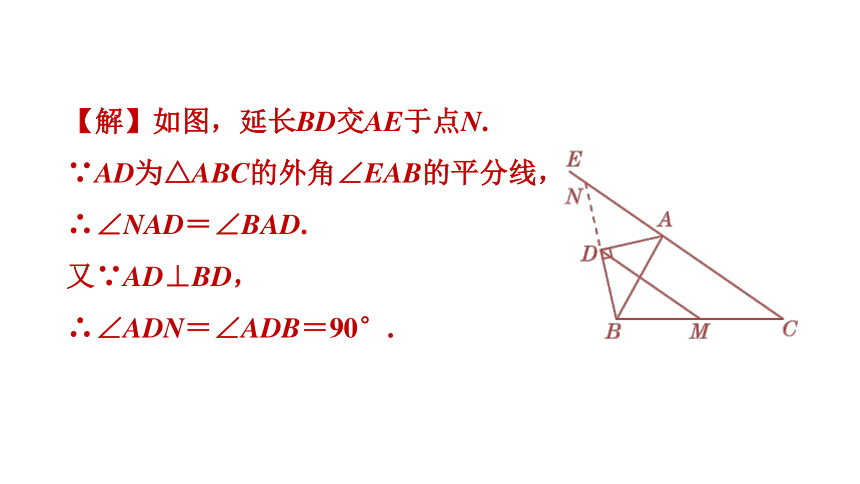
【解】如图,延长BD交AE于点N.
∵AD为△ABC的外角∠EAB的平分线,
∴∠NAD=∠BAD.
又∵AD⊥BD,
∴∠ADN=∠ADB=90°.
3 如图,在△ABC中,AB=6,AC=10,AD平分∠BAC,BD⊥AD于点D,点E为BC的中点,连接DE.求DE的长.
【解】如图,延长BD交AC于点F.
∵AD平分∠BAC,
∴∠BAD=∠FAD.
∵BD⊥AD,
∴∠ADB=∠ADF=90°.
方法 3 倍长法(延长)构造三角形的中位线
【点方法】
本题运用倍长法构造全等的三角形,再利用三角形的中位线定理解决.
5 如图,在四边形ABCD中,AB与CD不平行,M,N分别是AD,BC的中点.若AB=10,CD=8,求MN长度的取值范围.
方法 4 已知一边中点,取另一边中点构造三角形的中位线
6 [2023·天津中学月考]如图所示,在△ABC中,∠A=40°,D,E分别在AB,AC上,BD=CE,
BE,CD的中点分别是M,N,直线MN
分别交AB,AC于点P,Q,求∠APQ的
度数.
方法 5 已知两边中点,取第三边中点构造三角形的中位线
方法 6 平行四边形的对角线交点与三线合一构造中位线
微专题
构造三角形中位线的常用方法
北师版 八年级下
例
典 例 剖 析
证明:如图,延长AM,AN分别交BC于点F,G.
∵BD平分∠ABC,AN⊥BD,
∴∠ABN=∠GBN,∠ANB=∠GNB=90°.
又∵BN=BN,
∴△ABN≌△GBN(ASA).
∴AN=NG,AB=BG.
方法 1 连接两点构造三角形的中位线
分 类 训 练
1 [2023·成都外国语学校模拟]如图,在 ABCD中,对角线AC,BD相交于点O,∠BCD的平分线交边AB于点E,BF⊥CE于点F.
(1)求证:CF=EF;
(2)连接OF,若CD=9,AD=6,求OF的长.
(1)求证:CF=EF;
【证明】在 ABCD中,AB与CD平行,
∴∠DCE=∠BEC.
∵CE平分∠BCD,∴∠DCE=∠BCE,
∴∠BEC=∠BCE,∴BC=BE.
∵BF⊥CE,∴CF=EF.
(2)连接OF,若CD=9,AD=6,求OF的长.
2 如图,在△ABC中,点M为BC的中点,AD为△ABC的外角∠EAB的平分线,且AD⊥BD.若AB=12,AC=18,连接DM,求DM的长.
方法 2 利用角平分线和垂直构造三角形的中位线
【解】如图,延长BD交AE于点N.
∵AD为△ABC的外角∠EAB的平分线,
∴∠NAD=∠BAD.
又∵AD⊥BD,
∴∠ADN=∠ADB=90°.
3 如图,在△ABC中,AB=6,AC=10,AD平分∠BAC,BD⊥AD于点D,点E为BC的中点,连接DE.求DE的长.
【解】如图,延长BD交AC于点F.
∵AD平分∠BAC,
∴∠BAD=∠FAD.
∵BD⊥AD,
∴∠ADB=∠ADF=90°.
方法 3 倍长法(延长)构造三角形的中位线
【点方法】
本题运用倍长法构造全等的三角形,再利用三角形的中位线定理解决.
5 如图,在四边形ABCD中,AB与CD不平行,M,N分别是AD,BC的中点.若AB=10,CD=8,求MN长度的取值范围.
方法 4 已知一边中点,取另一边中点构造三角形的中位线
6 [2023·天津中学月考]如图所示,在△ABC中,∠A=40°,D,E分别在AB,AC上,BD=CE,
BE,CD的中点分别是M,N,直线MN
分别交AB,AC于点P,Q,求∠APQ的
度数.
方法 5 已知两边中点,取第三边中点构造三角形的中位线
方法 6 平行四边形的对角线交点与三线合一构造中位线
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
