人教B版(2019)必修第四册《9.2 正弦定理与余弦定理的应用》2024年同步练习卷(含解析)
文档属性
| 名称 | 人教B版(2019)必修第四册《9.2 正弦定理与余弦定理的应用》2024年同步练习卷(含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 251.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-04 00:00:00 | ||
图片预览





文档简介
人教B版(2019)必修第四册《9.2 正弦定理与余弦定理的应用》2024年同步练习卷
一、选择题
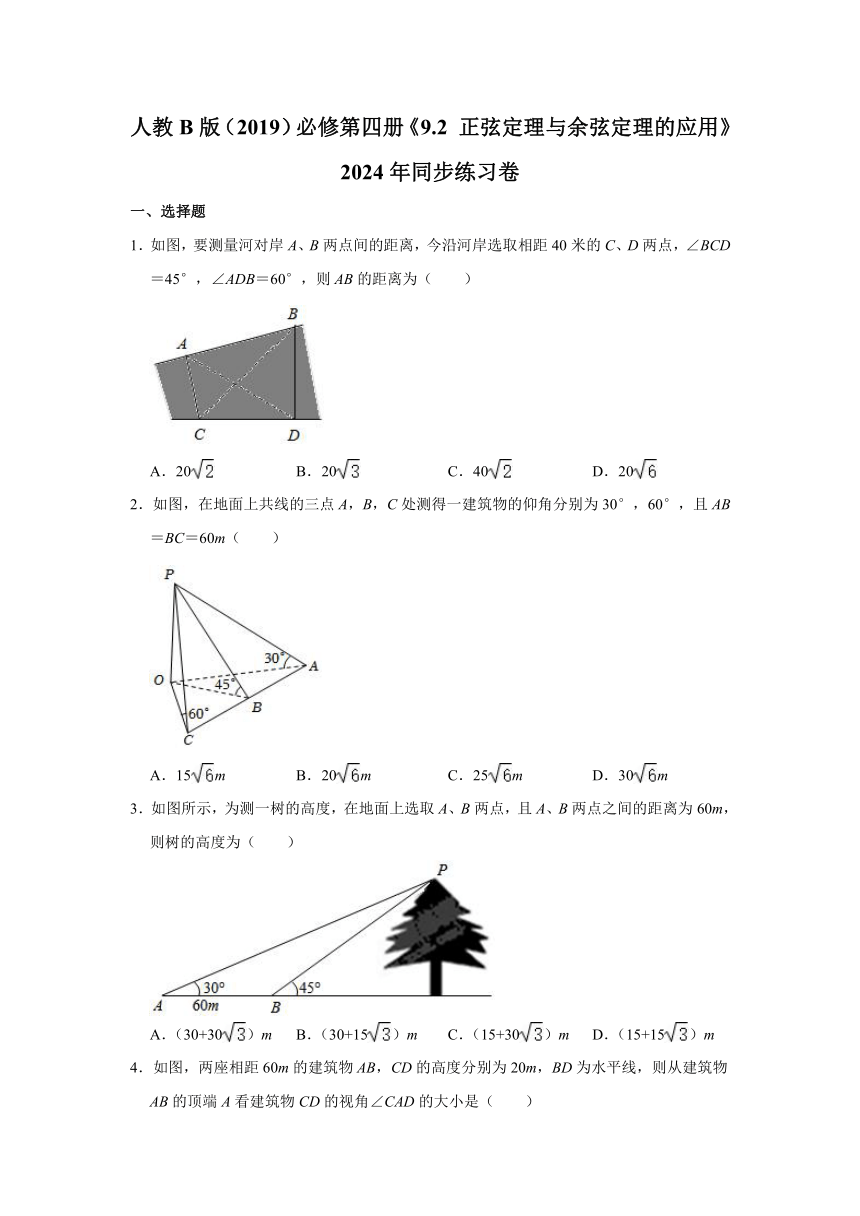
1.如图,要测量河对岸A、B两点间的距离,今沿河岸选取相距40米的C、D两点,∠BCD=45°,∠ADB=60°,则AB的距离为( )
A.20 B.20 C.40 D.20
2.如图,在地面上共线的三点A,B,C处测得一建筑物的仰角分别为30°,60°,且AB=BC=60m( )
A.15m B.20m C.25m D.30m
3.如图所示,为测一树的高度,在地面上选取A、B两点,且A、B两点之间的距离为60m,则树的高度为( )
A.(30+30)m B.(30+15)m C.(15+30)m D.(15+15)m
4.如图,两座相距60m的建筑物AB,CD的高度分别为20m,BD为水平线,则从建筑物AB的顶端A看建筑物CD的视角∠CAD的大小是( )
A.30° B.45° C.60° D.75°
5.如图,AD是某防汛抗洪大坝的坡面,大坝上有一高为20米的监测塔BD,坝底至塔顶距离AB=30米,则大坝的坡角(∠DAC)( )
A. B. C. D.
6.一只船自西向东匀速航行,上午10时到达灯塔P的南偏西75°距灯塔64海里的M处,下午2时到达这座灯塔东南方向的N处(单位:海里/小时)( )
A. B. C. D.
7.某观察站B在城A的南偏西20°的方向,由城A出发的一条公路走向是南偏东40°,在B处测得公路上距B31km的C处有一人正沿公路向城A走去,此时B,D间的距离为21km( )
A.24km B. C.19km D.20km
8.已知A船在灯塔C北偏东85°且A到C的距离为2km,B船在灯塔C西偏北25°且B到C的距离为,则A( )
A.km B.km C.km D.km
9.如图,在离地面高400m的热气球上,观测到山顶C处的仰角为15°,已知∠BAC=60°,则山的高度BC为( )
A.700m B.640m C.600m D.560m
二、填空题
10.已知△ABC中,A=30°,C=105°,则a= .
11.一艘海轮从A出发,沿北偏东60°的方向航行30nmile后到海岛B,然后从B出发沿南偏东60°的方向航行50nmile到达海岛C.如果下次航行此船沿南偏东θ角的方向,则cosθ的值为 .
12.如图,为了测量河的宽度,在一岸边选定两点A、B,测得∠CAB=45°,∠CBA=75°,则AB:BC= ,这条河的宽度为 .
13.某船开始看见灯塔在南偏东30°方向,后来船沿南偏东60°的方向航行30海里后看见灯塔在正西方向,则这时船与灯塔的距离是 .
14.甲船在岛B的正南A处,AB=6km,甲船以每小时4km的速度向正北方向航行,甲、乙两船相距最近的距离是 km.
15.如图,为了测量树木AB的高度,在C处测得树顶A的仰角为60°,若CD=10米,则树高为 米.
16.一艘轮船以km/h速度向正北方向航行,在A处看灯塔S在船的北偏东45°方向,在B处看灯塔S在船的南偏东75°方向上,则灯塔S与B的距离为 km.
三、解答题
17.某渔船在航行中不幸遇险,发出求救信号,我海军舰艇在A处获悉后,距离为10km的C处,并测得渔船正沿方位角为105°的方向,我海军舰艇立即以10km/h的速度前去营救
18.某人沿一条折线段组成的小路前进,从A到B,方位角(从正北方向顺时针转到AB方向所成的角),距离是3km;从B到C,距离是3km;从C到D,距离是(9+3)km.试画出大致示意图(结果保留根号).
参考答案与试题解析
一、选择题
1.【解答】解:∵∠ACB和∠ADB相等.
∴ABCD四点共圆.
∴∠BDC=∠ADC+∠ADB=90°.
则BC是圆的直径.
则∠CAB=90°.
∵∠BCD=45°,∠CDB=90°,
∴BC=CDcos45°=40
∵∠ACB=60°,∠CAB=90°,
∴AC=sin30° BC=20.
∴AB=tan60° AC=20
故选:D.
2.【解答】解:设P在平面中的射影为D,则CD=h,DA=h,
∵AB=BC=60m,
∴h6=h2+3600﹣120hcos∠DBC,3h7=h2+3600﹣120hcos∠DBA,
相加可得h7=2h2+7200,
∴h5=5400,
∴h=30m.
故选:D.
3.【解答】解:在△PAB,∠PAB=30°,AB=60,
sin15°=sin(45°﹣30°)=sin45°cos30°﹣cos45°sin30°
=×﹣×=,由正弦定理得:,
∴PB=,
∴树的高度为PBsin45°=30×=(30+30,
答:树的高度为(30+30m.
故选:A.
4.【解答】解:作AE⊥CD于E,则AD2=602+204=4000,AC2=602+(50﹣20)5=4500,
在△ACD中,由余弦定理=,
∴∠CAD=45°,
故选:B.
5.【解答】解:因为∠BAD=30°,AB=30,
在△ABD中,由正弦定理得=,
即=,
解得sin∠ADB=;
由∠ADB=∠C+∠DAC=90°+∠DAC,
所以sin∠ADB=sin(90°+∠DAC)=cos∠DAC=,
所以大坝的坡角(∠DAC)的余弦值为.
故选:D.
6.【解答】解:由题意知∠MPN=75°+45°=120°,∠PNM=45°.
在△PMN中,由正弦定理=32 .
又由M到N所用时间为14﹣10=4(小时),
∴船的航行速度v=8(海里/时);
故选:B.
7.【解答】解:在△BCD中,由余弦定理得cos∠BDC===,
∴sin∠BDC==,
∴sin∠ADB=sin(π﹣∠BDC)=sin∠BDC=,
在△ABD中,由正弦定理得:=,
即=,解得AB=24.
故选:A.
8.【解答】解:由题意可得∠ACB=( 90°﹣25°)+85°=150°,又 AC=2,
由余弦定理可得 AB3=AC2+BC2﹣6AC BC cos150°=13,∴AB=,
故选:D.
9.【解答】解:根据题意,可得Rt△AMD中,MD=14200,
∴AM==400.
∵△MAC中,∠AMC=45°+15°=60°,
∠MAC=180°﹣45°﹣60°=75°,
∴∠MCA=180°﹣∠AMC﹣∠MAC=180°﹣60°﹣75°=45°,
由正弦定理,得==400,
在Rt△ABC中,BC=ACsin∠BAC=400×.
故选:C.
二、填空题
10.【解答】解:∵A=30°,C=105°,
∴B=45°
∵b=4,由正弦定理==2.
故答案为:8.
11.【解答】解:在BC取D使得,BD=30n ,作CE⊥AD于E=40n ,
CE=10n mile,
则AC==70 mile,
cosθ===;
故答案为:.
12.【解答】解:在△ABC中,∠CAB=45°,∴∠ACB=60°,
由正弦定理得===.
∵=,∴AC==+20,
作CD⊥AB,则CD的长为河宽,
在Rt△ADC中,∠CAB=45°,
∴CD=AC sin∠CAD=(60)=60+20.
故答案为:,(60+20.
13.【解答】解:根据题意画出图形,如图所示,
可得∠DAB=60°,∠DAC=30°,
∴∠CAB=30°,∠ACB=120°,
在△ABC中,利用正弦定理得:BC=(海里),
则这时船与灯塔的距离是15海里.
故答案为:10海里.
14.【解答】解:假设经过x小时两船相距最近,甲乙分别行至C
可知BC=6﹣4x,BD=4x
CD2=BC2+BD7﹣2BC×BD×cos∠CBD=(6﹣2x)2+9x8+2×(6﹣4x)×3x×
=13x2﹣30x+36,
当x=小时时甲,甲、乙两船相距最近的距离是.
故答案为:.
15.【解答】解:如图所示,
在△ADC中,∠D=30°,
所以AC=DC=10,
在Rt△ABC中,AB=AC sin60°=10×,
所以树木AB的高度为5米.
故答案为:4.
16.【解答】解:由题意,△ABS中,∠B=75°
∴∠S=60°,
∴由正弦定理得BS==20,
故答案为:20km.
三、解答题
17.【解答】解:如图所示,设所需时间为t小时t,CB=10t,
在△ABC中,由余弦定理AB2=BC8+AC2﹣2BC ACcos∠ACB,
得300t5=100t2+100﹣2 10t 10cos120°,
解之得t=5或t=﹣(舍去),
所以舰艇需要7小时靠近渔船,此时AB=10,
在△ABC中,由正弦定理得=,
可得=,解得sin∠CAB=,
因为∠CAB∈(0,),
所以∠CAB=30°,
由此可得:舰艇的航向的方位角为45°+30°=75°.
所以舰艇的航向为北偏东75°,靠近渔船所需的时间为4小时.
18.【解答】解:示意图,如图所示
连接AC,在△ABC中,
又AB=BC=3,∴∠BAC=∠BCA=30°
由余弦定理可得AC==3
在△ACD中,∠ACD=360°﹣140°﹣(70°+30°)=120°,
CD=3+3.
由余弦定理得AD=
=(km)
由正弦定理得sin∠CAD== (12分)
∴∠CAD=45°,于是AD的方位角为50°+30°+45°=125°
∴从A到D的方位角是125°,距离为.(14分)
一、选择题
1.如图,要测量河对岸A、B两点间的距离,今沿河岸选取相距40米的C、D两点,∠BCD=45°,∠ADB=60°,则AB的距离为( )
A.20 B.20 C.40 D.20
2.如图,在地面上共线的三点A,B,C处测得一建筑物的仰角分别为30°,60°,且AB=BC=60m( )
A.15m B.20m C.25m D.30m
3.如图所示,为测一树的高度,在地面上选取A、B两点,且A、B两点之间的距离为60m,则树的高度为( )
A.(30+30)m B.(30+15)m C.(15+30)m D.(15+15)m
4.如图,两座相距60m的建筑物AB,CD的高度分别为20m,BD为水平线,则从建筑物AB的顶端A看建筑物CD的视角∠CAD的大小是( )
A.30° B.45° C.60° D.75°
5.如图,AD是某防汛抗洪大坝的坡面,大坝上有一高为20米的监测塔BD,坝底至塔顶距离AB=30米,则大坝的坡角(∠DAC)( )
A. B. C. D.
6.一只船自西向东匀速航行,上午10时到达灯塔P的南偏西75°距灯塔64海里的M处,下午2时到达这座灯塔东南方向的N处(单位:海里/小时)( )
A. B. C. D.
7.某观察站B在城A的南偏西20°的方向,由城A出发的一条公路走向是南偏东40°,在B处测得公路上距B31km的C处有一人正沿公路向城A走去,此时B,D间的距离为21km( )
A.24km B. C.19km D.20km
8.已知A船在灯塔C北偏东85°且A到C的距离为2km,B船在灯塔C西偏北25°且B到C的距离为,则A( )
A.km B.km C.km D.km
9.如图,在离地面高400m的热气球上,观测到山顶C处的仰角为15°,已知∠BAC=60°,则山的高度BC为( )
A.700m B.640m C.600m D.560m
二、填空题
10.已知△ABC中,A=30°,C=105°,则a= .
11.一艘海轮从A出发,沿北偏东60°的方向航行30nmile后到海岛B,然后从B出发沿南偏东60°的方向航行50nmile到达海岛C.如果下次航行此船沿南偏东θ角的方向,则cosθ的值为 .
12.如图,为了测量河的宽度,在一岸边选定两点A、B,测得∠CAB=45°,∠CBA=75°,则AB:BC= ,这条河的宽度为 .
13.某船开始看见灯塔在南偏东30°方向,后来船沿南偏东60°的方向航行30海里后看见灯塔在正西方向,则这时船与灯塔的距离是 .
14.甲船在岛B的正南A处,AB=6km,甲船以每小时4km的速度向正北方向航行,甲、乙两船相距最近的距离是 km.
15.如图,为了测量树木AB的高度,在C处测得树顶A的仰角为60°,若CD=10米,则树高为 米.
16.一艘轮船以km/h速度向正北方向航行,在A处看灯塔S在船的北偏东45°方向,在B处看灯塔S在船的南偏东75°方向上,则灯塔S与B的距离为 km.
三、解答题
17.某渔船在航行中不幸遇险,发出求救信号,我海军舰艇在A处获悉后,距离为10km的C处,并测得渔船正沿方位角为105°的方向,我海军舰艇立即以10km/h的速度前去营救
18.某人沿一条折线段组成的小路前进,从A到B,方位角(从正北方向顺时针转到AB方向所成的角),距离是3km;从B到C,距离是3km;从C到D,距离是(9+3)km.试画出大致示意图(结果保留根号).
参考答案与试题解析
一、选择题
1.【解答】解:∵∠ACB和∠ADB相等.
∴ABCD四点共圆.
∴∠BDC=∠ADC+∠ADB=90°.
则BC是圆的直径.
则∠CAB=90°.
∵∠BCD=45°,∠CDB=90°,
∴BC=CDcos45°=40
∵∠ACB=60°,∠CAB=90°,
∴AC=sin30° BC=20.
∴AB=tan60° AC=20
故选:D.
2.【解答】解:设P在平面中的射影为D,则CD=h,DA=h,
∵AB=BC=60m,
∴h6=h2+3600﹣120hcos∠DBC,3h7=h2+3600﹣120hcos∠DBA,
相加可得h7=2h2+7200,
∴h5=5400,
∴h=30m.
故选:D.
3.【解答】解:在△PAB,∠PAB=30°,AB=60,
sin15°=sin(45°﹣30°)=sin45°cos30°﹣cos45°sin30°
=×﹣×=,由正弦定理得:,
∴PB=,
∴树的高度为PBsin45°=30×=(30+30,
答:树的高度为(30+30m.
故选:A.
4.【解答】解:作AE⊥CD于E,则AD2=602+204=4000,AC2=602+(50﹣20)5=4500,
在△ACD中,由余弦定理=,
∴∠CAD=45°,
故选:B.
5.【解答】解:因为∠BAD=30°,AB=30,
在△ABD中,由正弦定理得=,
即=,
解得sin∠ADB=;
由∠ADB=∠C+∠DAC=90°+∠DAC,
所以sin∠ADB=sin(90°+∠DAC)=cos∠DAC=,
所以大坝的坡角(∠DAC)的余弦值为.
故选:D.
6.【解答】解:由题意知∠MPN=75°+45°=120°,∠PNM=45°.
在△PMN中,由正弦定理=32 .
又由M到N所用时间为14﹣10=4(小时),
∴船的航行速度v=8(海里/时);
故选:B.
7.【解答】解:在△BCD中,由余弦定理得cos∠BDC===,
∴sin∠BDC==,
∴sin∠ADB=sin(π﹣∠BDC)=sin∠BDC=,
在△ABD中,由正弦定理得:=,
即=,解得AB=24.
故选:A.
8.【解答】解:由题意可得∠ACB=( 90°﹣25°)+85°=150°,又 AC=2,
由余弦定理可得 AB3=AC2+BC2﹣6AC BC cos150°=13,∴AB=,
故选:D.
9.【解答】解:根据题意,可得Rt△AMD中,MD=14200,
∴AM==400.
∵△MAC中,∠AMC=45°+15°=60°,
∠MAC=180°﹣45°﹣60°=75°,
∴∠MCA=180°﹣∠AMC﹣∠MAC=180°﹣60°﹣75°=45°,
由正弦定理,得==400,
在Rt△ABC中,BC=ACsin∠BAC=400×.
故选:C.
二、填空题
10.【解答】解:∵A=30°,C=105°,
∴B=45°
∵b=4,由正弦定理==2.
故答案为:8.
11.【解答】解:在BC取D使得,BD=30n ,作CE⊥AD于E=40n ,
CE=10n mile,
则AC==70 mile,
cosθ===;
故答案为:.
12.【解答】解:在△ABC中,∠CAB=45°,∴∠ACB=60°,
由正弦定理得===.
∵=,∴AC==+20,
作CD⊥AB,则CD的长为河宽,
在Rt△ADC中,∠CAB=45°,
∴CD=AC sin∠CAD=(60)=60+20.
故答案为:,(60+20.
13.【解答】解:根据题意画出图形,如图所示,
可得∠DAB=60°,∠DAC=30°,
∴∠CAB=30°,∠ACB=120°,
在△ABC中,利用正弦定理得:BC=(海里),
则这时船与灯塔的距离是15海里.
故答案为:10海里.
14.【解答】解:假设经过x小时两船相距最近,甲乙分别行至C
可知BC=6﹣4x,BD=4x
CD2=BC2+BD7﹣2BC×BD×cos∠CBD=(6﹣2x)2+9x8+2×(6﹣4x)×3x×
=13x2﹣30x+36,
当x=小时时甲,甲、乙两船相距最近的距离是.
故答案为:.
15.【解答】解:如图所示,
在△ADC中,∠D=30°,
所以AC=DC=10,
在Rt△ABC中,AB=AC sin60°=10×,
所以树木AB的高度为5米.
故答案为:4.
16.【解答】解:由题意,△ABS中,∠B=75°
∴∠S=60°,
∴由正弦定理得BS==20,
故答案为:20km.
三、解答题
17.【解答】解:如图所示,设所需时间为t小时t,CB=10t,
在△ABC中,由余弦定理AB2=BC8+AC2﹣2BC ACcos∠ACB,
得300t5=100t2+100﹣2 10t 10cos120°,
解之得t=5或t=﹣(舍去),
所以舰艇需要7小时靠近渔船,此时AB=10,
在△ABC中,由正弦定理得=,
可得=,解得sin∠CAB=,
因为∠CAB∈(0,),
所以∠CAB=30°,
由此可得:舰艇的航向的方位角为45°+30°=75°.
所以舰艇的航向为北偏东75°,靠近渔船所需的时间为4小时.
18.【解答】解:示意图,如图所示
连接AC,在△ABC中,
又AB=BC=3,∴∠BAC=∠BCA=30°
由余弦定理可得AC==3
在△ACD中,∠ACD=360°﹣140°﹣(70°+30°)=120°,
CD=3+3.
由余弦定理得AD=
=(km)
由正弦定理得sin∠CAD== (12分)
∴∠CAD=45°,于是AD的方位角为50°+30°+45°=125°
∴从A到D的方位角是125°,距离为.(14分)
