冀教版四年级数学下册第五单元分数与除法(课件)(共25张PPT)
文档属性
| 名称 | 冀教版四年级数学下册第五单元分数与除法(课件)(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-04 00:00:00 | ||
图片预览







文档简介
(共25张PPT)
分数的意义和性质
——分数与除法(1)
一、复习回顾
中分数单位最大的是( )。
2、2米长的绳子平均剪成5段,每段是这根绳子的( )。
比较大小
一根
1、
3、
同分母分数,分子大的分数就大。
同分子分数,分母大的分数反而小。
一、复习回顾
将6米的彩带平均分给3个小朋友,每人分得几米?
6÷3=2(米)
将1米彩带平均分给2个小朋友,每人分得几米?
1÷2=0.5(米)
分数不但可以表示部分与整体的关系,还可以表示具体的数量。
当分数表示具体的数量时,需要加单位名称。
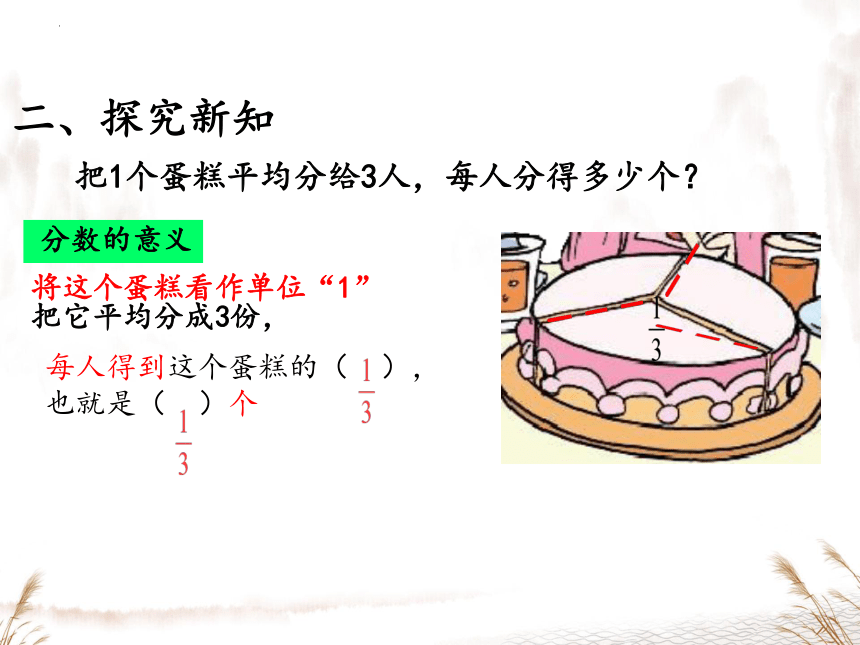
二、探究新知
把1个蛋糕平均分给3人,每人分得多少个?
除法的意义
把1个蛋糕平均分成3份,求每份是多少,即每人分得多少个?
用除法算式,列式为
二、探究新知
把1个蛋糕平均分给3人,每人分得多少个?
分数的意义
将这个蛋糕看作单位“1”
每人得到这个蛋糕的( ),
也就是( )个
把它平均分成3份,
二、探究新知—感知分数与除法的关系
把1个蛋糕平均分给3人,每人分得多少个?
规范解答
(个)
答:每人分得 个。
二、探究新知—感知分数与除法的关系
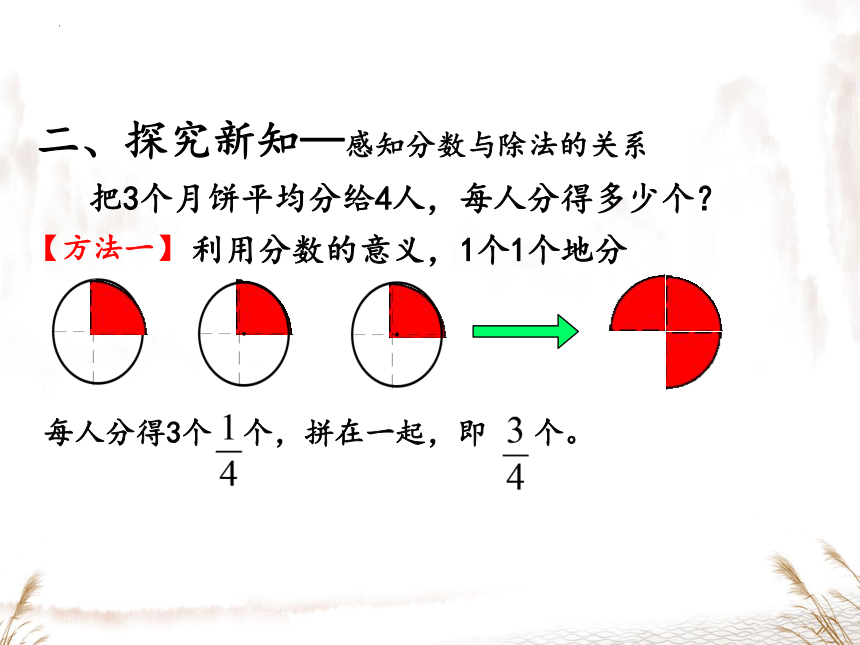
把3个月饼平均分给4人,每人分得多少个?
该怎样解决这个问题呢?
二、探究新知—感知分数与除法的关系
把3个月饼平均分给4人,每人分得多少个?
利用分数的意义,1个1个地分
【方法一】
每人分得3个 个,拼在一起,即 个。
二、探究新知—感知分数与除法的关系
把3个月饼平均分给4人,每人分得多少个?
利用除法的含义
【方法二】
3个月饼平均给4份,求每份是多少,即每人分得多少个。
用除法计算,列式为3÷4
二、探究新知—感知分数与除法的关系
把3个月饼平均分给4人,每人分得多少个?
利用分数的意义,3个摞在一起分
3个月饼的
1个月饼的
个
二、探究新知—感知分数与除法的关系
3个月饼的
1个月饼的
个
表示单位“1”平均分成4份,其中的3份是多少;
还表示把3平均分成4份,其中的1份是多少。
二、探究新知—感知分数与除法的关系
把3个月饼平均分给4人,每人分得多少个?
规范解答
答:每人分得 个。
二、探究新知—感知分数与除法的关系
把1米的彩带平均分成2份,每份是多少米?3份呢
规范解答
(米)
答:每份是 米。
答:每份是 米。
二、探究新知—感知分数与除法的关系
计算结果得不到整数时,除了用小数,可以用分数来表示。
6÷3=2
1÷2=0.5
二、探究新知—归纳分数与除法的关系
观察算式,你发现分数和除法有什么关系吗?
想一想:为什么b≠0?
除数不能为0!
分母
分子
二、探究新知—分数与除法的联系与区别
想一想:分数和除法之间有什么联系和区别呢?
三、巩固练习
:把单位“1”平均分成( )份,表示其中( )份的数;还表示把( )平均分成( )份,表示其中( )份的数。
5
2
2
5
1
三、巩固练习
在括号里填上适当的数。
在括号里填上适当的数。
答:每个茶叶筒装 千克。
巩固练习
答:正方形的边长是 米。
一个 3 m2 的花坛,种 4 种花,每种花平均占地多少平方米? 5 种呢?(用分数表示。)
三、巩固练习
答:种4种花,每种花平均占地 ,
种5种花,每种花平均占地 。
四、课堂小结
分子
分母
除数
被除数
分数的意义和性质
——分数与除法(1)
一、复习回顾
中分数单位最大的是( )。
2、2米长的绳子平均剪成5段,每段是这根绳子的( )。
比较大小
一根
1、
3、
同分母分数,分子大的分数就大。
同分子分数,分母大的分数反而小。
一、复习回顾
将6米的彩带平均分给3个小朋友,每人分得几米?
6÷3=2(米)
将1米彩带平均分给2个小朋友,每人分得几米?
1÷2=0.5(米)
分数不但可以表示部分与整体的关系,还可以表示具体的数量。
当分数表示具体的数量时,需要加单位名称。
二、探究新知
把1个蛋糕平均分给3人,每人分得多少个?
除法的意义
把1个蛋糕平均分成3份,求每份是多少,即每人分得多少个?
用除法算式,列式为
二、探究新知
把1个蛋糕平均分给3人,每人分得多少个?
分数的意义
将这个蛋糕看作单位“1”
每人得到这个蛋糕的( ),
也就是( )个
把它平均分成3份,
二、探究新知—感知分数与除法的关系
把1个蛋糕平均分给3人,每人分得多少个?
规范解答
(个)
答:每人分得 个。
二、探究新知—感知分数与除法的关系
把3个月饼平均分给4人,每人分得多少个?
该怎样解决这个问题呢?
二、探究新知—感知分数与除法的关系
把3个月饼平均分给4人,每人分得多少个?
利用分数的意义,1个1个地分
【方法一】
每人分得3个 个,拼在一起,即 个。
二、探究新知—感知分数与除法的关系
把3个月饼平均分给4人,每人分得多少个?
利用除法的含义
【方法二】
3个月饼平均给4份,求每份是多少,即每人分得多少个。
用除法计算,列式为3÷4
二、探究新知—感知分数与除法的关系
把3个月饼平均分给4人,每人分得多少个?
利用分数的意义,3个摞在一起分
3个月饼的
1个月饼的
个
二、探究新知—感知分数与除法的关系
3个月饼的
1个月饼的
个
表示单位“1”平均分成4份,其中的3份是多少;
还表示把3平均分成4份,其中的1份是多少。
二、探究新知—感知分数与除法的关系
把3个月饼平均分给4人,每人分得多少个?
规范解答
答:每人分得 个。
二、探究新知—感知分数与除法的关系
把1米的彩带平均分成2份,每份是多少米?3份呢
规范解答
(米)
答:每份是 米。
答:每份是 米。
二、探究新知—感知分数与除法的关系
计算结果得不到整数时,除了用小数,可以用分数来表示。
6÷3=2
1÷2=0.5
二、探究新知—归纳分数与除法的关系
观察算式,你发现分数和除法有什么关系吗?
想一想:为什么b≠0?
除数不能为0!
分母
分子
二、探究新知—分数与除法的联系与区别
想一想:分数和除法之间有什么联系和区别呢?
三、巩固练习
:把单位“1”平均分成( )份,表示其中( )份的数;还表示把( )平均分成( )份,表示其中( )份的数。
5
2
2
5
1
三、巩固练习
在括号里填上适当的数。
在括号里填上适当的数。
答:每个茶叶筒装 千克。
巩固练习
答:正方形的边长是 米。
一个 3 m2 的花坛,种 4 种花,每种花平均占地多少平方米? 5 种呢?(用分数表示。)
三、巩固练习
答:种4种花,每种花平均占地 ,
种5种花,每种花平均占地 。
四、课堂小结
分子
分母
除数
被除数
