人教版七年级下册7.2.2 用坐标表示平移(含答案)
文档属性
| 名称 | 人教版七年级下册7.2.2 用坐标表示平移(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 260.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-05 00:00:00 | ||
图片预览

文档简介
7.2.2 用坐标表示平移
一、选择题
1.在平面直角坐标系中,将点(1,1)向右平移2个单位后,得到的点的坐标是( )
A.(3,1) B.(-1,1) C.(1,3) D.(1,-1)
2.在平面直角坐标系中,将点P(-3,2)向下平移4个单位得到点P′,则点P′所在的象限为( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.在平面直角坐标系中,将点A(1,-2)向上平移3个单位长度,再向左平移2个单位长度,得到点B,则点B的坐标是( )
A.(-1,1) B.(3,1) C.(4,-4) D.(4,0)
4.如图,把三角形ABC先向右平移3个单位,再向上平移2个单位得到三角形DEF,则顶点C(0,-1)的对应点坐标为( )
A.(0,0) B.(1,2) C.(1,3) D.(3,1)
5.如图,点A(2,1),将线段OA先向上平移2个单位长度,再向左平移3个单位长度,得到线段O′A′,则点A的对应点A′的坐标是( )
A.(-3,2) B.(0,4) C.(-1,3) D.(3,-1)
6.如图,在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(0,1),将线段AB平移,使其一个端点到C(3,2),则平移后另一端点的坐标为( )
A.(1,3) B.(5,1) C.(1,3)或(3,5) D.(1,3)或(5,1)
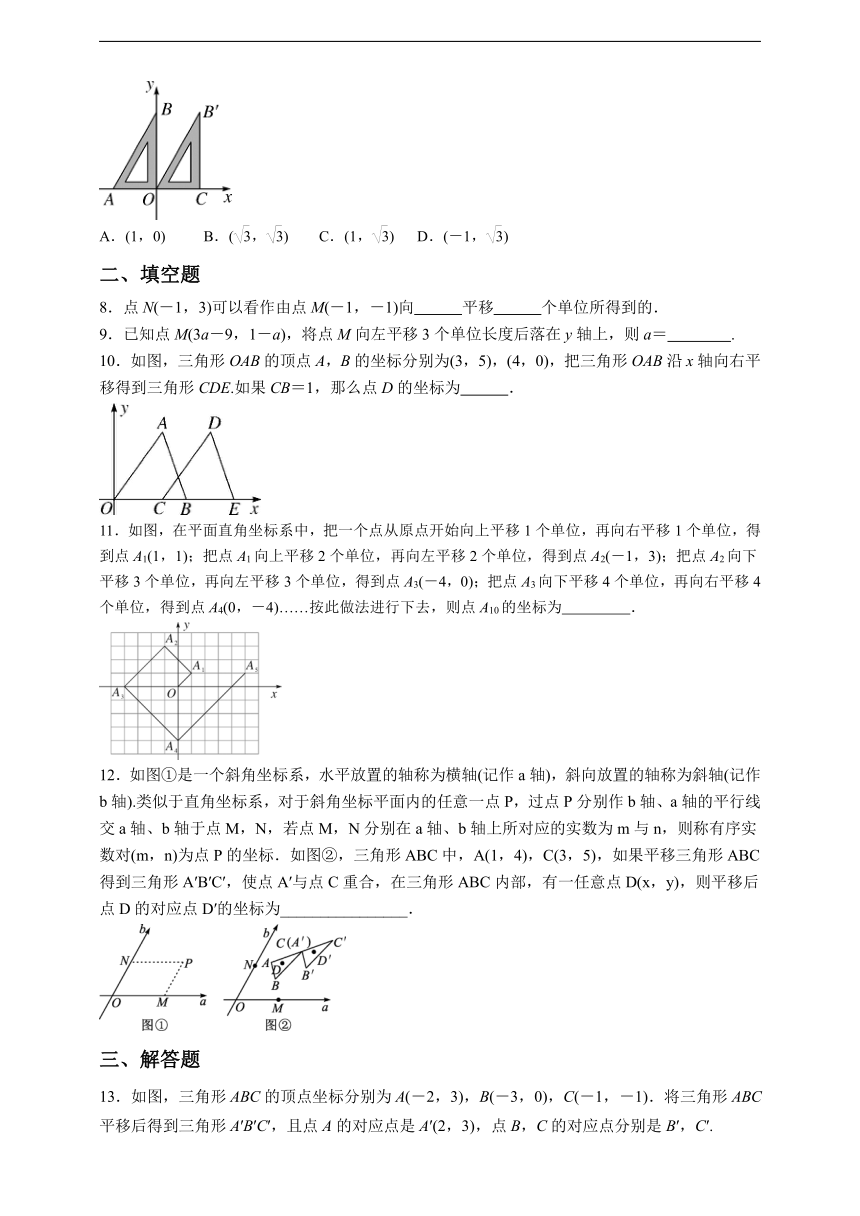
7.如图,已知一个直角三角板的直角顶点与原点重合,另两个顶点A,B的坐标分别为(-1,0),(0,).现将该三角板向右平移使点A与点O重合,得到三角形OCB′,则点B的对应点B′的坐标是( )
A.(1,0) B.(,) C.(1,) D.(-1,)
二、填空题
8.点N(-1,3)可以看作由点M(-1,-1)向 平移 个单位所得到的.
9.已知点M(3a-9,1-a),将点M向左平移3个单位长度后落在y轴上,则a= .
10.如图,三角形OAB的顶点A,B的坐标分别为(3,5),(4,0),把三角形OAB沿x轴向右平移得到三角形CDE.如果CB=1,那么点D的坐标为 .
11.如图,在平面直角坐标系中,把一个点从原点开始向上平移1个单位,再向右平移1个单位,得到点A1(1,1);把点A1向上平移2个单位,再向左平移2个单位,得到点A2(-1,3);把点A2向下平移3个单位,再向左平移3个单位,得到点A3(-4,0);把点A3向下平移4个单位,再向右平移4个单位,得到点A4(0,-4)……按此做法进行下去,则点A10的坐标为 .
12.如图①是一个斜角坐标系,水平放置的轴称为横轴(记作a轴),斜向放置的轴称为斜轴(记作b轴).类似于直角坐标系,对于斜角坐标平面内的任意一点P,过点P分别作b轴、a轴的平行线交a轴、b轴于点M,N,若点M,N分别在a轴、b轴上所对应的实数为m与n,则称有序实数对(m,n)为点P的坐标.如图②,三角形ABC中,A(1,4),C(3,5),如果平移三角形ABC得到三角形A′B′C′,使点A′与点C重合,在三角形ABC内部,有一任意点D(x,y),则平移后点D的对应点D′的坐标为________________.
三、解答题
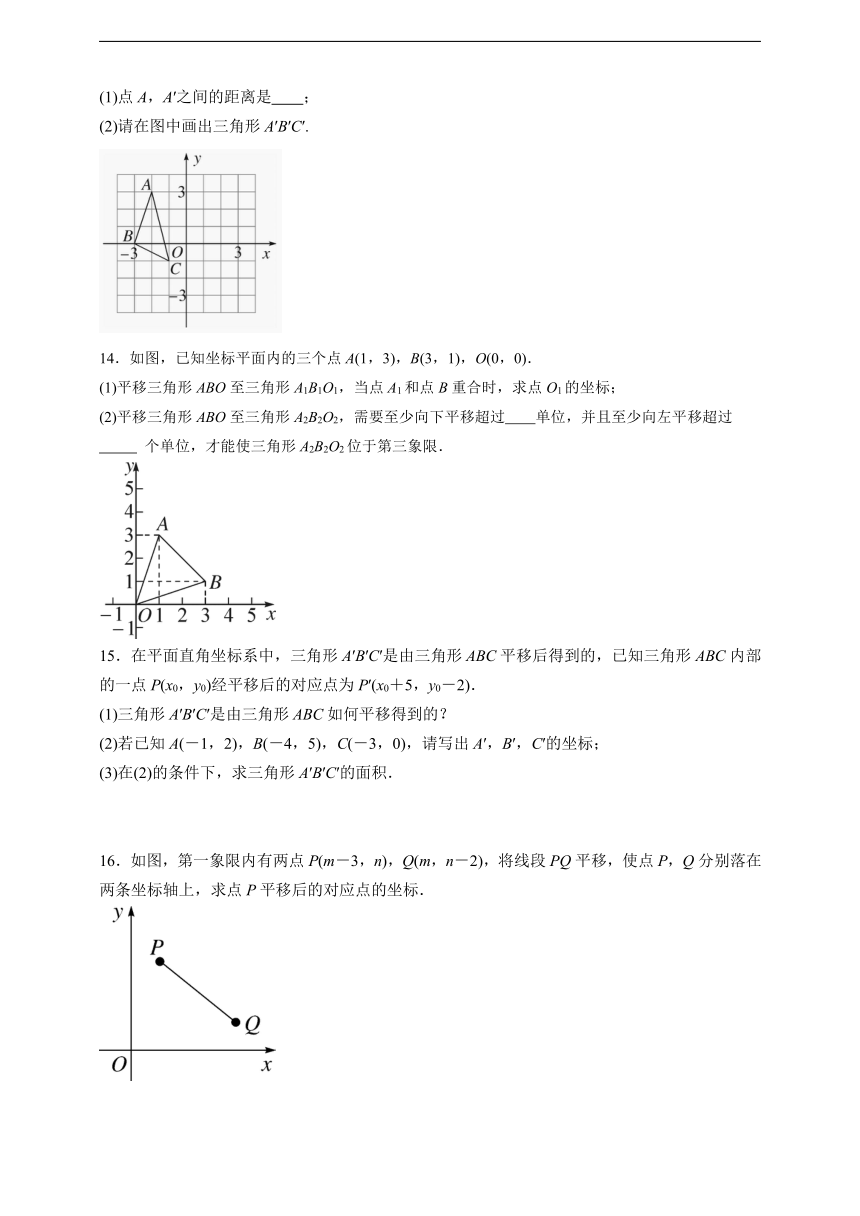
13.如图,三角形ABC的顶点坐标分别为A(-2,3),B(-3,0),C(-1,-1).将三角形ABC平移后得到三角形A′B′C′,且点A的对应点是A′(2,3),点B,C的对应点分别是B′,C′.
(1)点A,A′之间的距离是 ;
(2)请在图中画出三角形A′B′C′.
14.如图,已知坐标平面内的三个点A(1,3),B(3,1),O(0,0).
(1)平移三角形ABO至三角形A1B1O1,当点A1和点B重合时,求点O1的坐标;
(2)平移三角形ABO至三角形A2B2O2,需要至少向下平移超过 单位,并且至少向左平移超过
个单位,才能使三角形A2B2O2位于第三象限.
15.在平面直角坐标系中,三角形A′B′C′是由三角形ABC平移后得到的,已知三角形ABC内部的一点P(x0,y0)经平移后的对应点为P′(x0+5,y0-2).
(1)三角形A′B′C′是由三角形ABC如何平移得到的?
(2)若已知A(-1,2),B(-4,5),C(-3,0),请写出A′,B′,C′的坐标;
(3)在(2)的条件下,求三角形A′B′C′的面积.
16.如图,第一象限内有两点P(m-3,n),Q(m,n-2),将线段PQ平移,使点P,Q分别落在两条坐标轴上,求点P平移后的对应点的坐标.
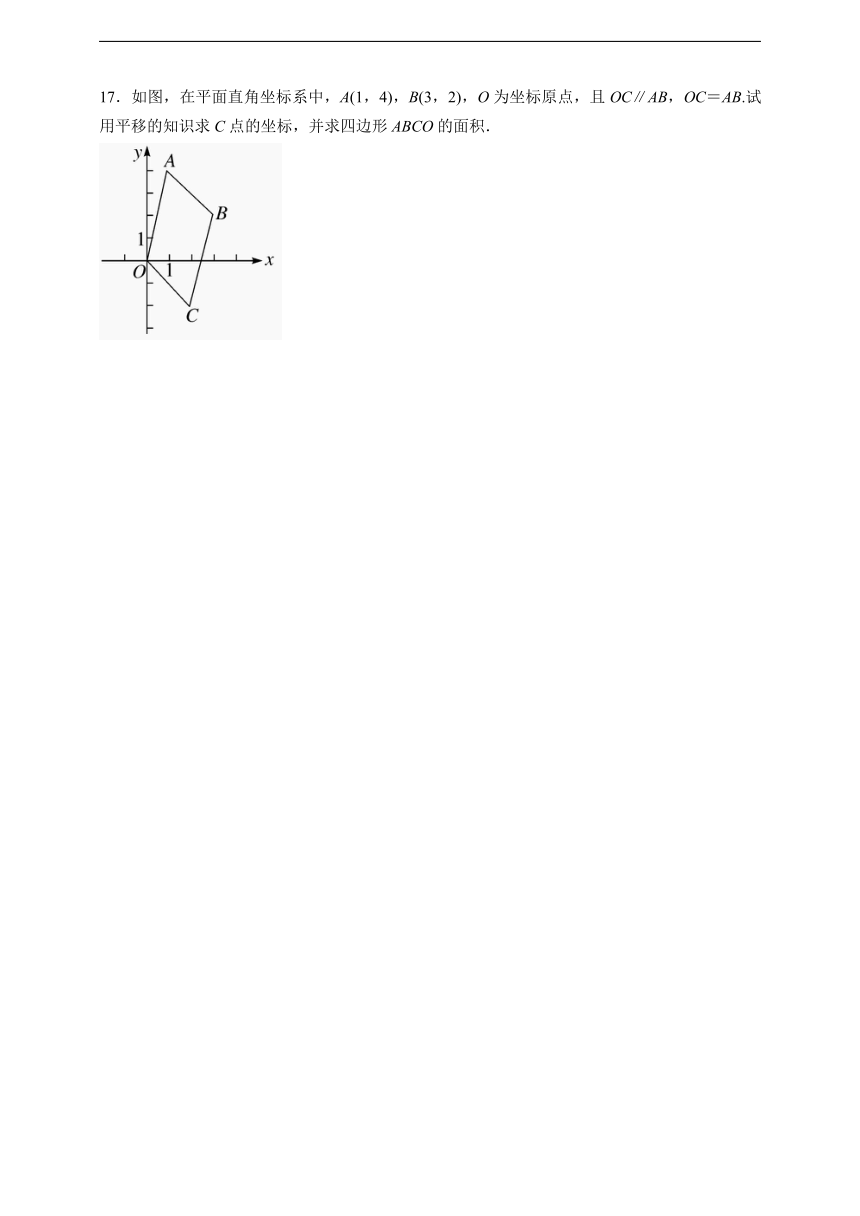
17.如图,在平面直角坐标系中,A(1,4),B(3,2),O为坐标原点,且OC∥AB,OC=AB.试用平移的知识求C点的坐标,并求四边形ABCO的面积.
参考答案
一、选择题
1.在平面直角坐标系中,将点(1,1)向右平移2个单位后,得到的点的坐标是( A )
A.(3,1) B.(-1,1) C.(1,3) D.(1,-1)
2.在平面直角坐标系中,将点P(-3,2)向下平移4个单位得到点P′,则点P′所在的象限为( C )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.在平面直角坐标系中,将点A(1,-2)向上平移3个单位长度,再向左平移2个单位长度,得到点B,则点B的坐标是( A )
A.(-1,1) B.(3,1) C.(4,-4) D.(4,0)
4.如图,把三角形ABC先向右平移3个单位,再向上平移2个单位得到三角形DEF,则顶点C(0,-1)的对应点坐标为( D )
A.(0,0) B.(1,2) C.(1,3) D.(3,1)
5.如图,点A(2,1),将线段OA先向上平移2个单位长度,再向左平移3个单位长度,得到线段O′A′,则点A的对应点A′的坐标是( C )
A.(-3,2) B.(0,4) C.(-1,3) D.(3,-1)
6.如图,在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(0,1),将线段AB平移,使其一个端点到C(3,2),则平移后另一端点的坐标为( D )
A.(1,3) B.(5,1) C.(1,3)或(3,5) D.(1,3)或(5,1)
7.如图,已知一个直角三角板的直角顶点与原点重合,另两个顶点A,B的坐标分别为(-1,0),(0,).现将该三角板向右平移使点A与点O重合,得到三角形OCB′,则点B的对应点B′的坐标是( C )
A.(1,0) B.(,) C.(1,) D.(-1,)
二、填空题
8.点N(-1,3)可以看作由点M(-1,-1)向 平移 个单位所得到的.
【答案】上 4
9.已知点M(3a-9,1-a),将点M向左平移3个单位长度后落在y轴上,则a= .
【答案】4
10.如图,三角形OAB的顶点A,B的坐标分别为(3,5),(4,0),把三角形OAB沿x轴向右平移得到三角形CDE.如果CB=1,那么点D的坐标为 .
【答案】(6,5)
11.如图,在平面直角坐标系中,把一个点从原点开始向上平移1个单位,再向右平移1个单位,得到点A1(1,1);把点A1向上平移2个单位,再向左平移2个单位,得到点A2(-1,3);把点A2向下平移3个单位,再向左平移3个单位,得到点A3(-4,0);把点A3向下平移4个单位,再向右平移4个单位,得到点A4(0,-4)……按此做法进行下去,则点A10的坐标为 .
【答案】(-1,11)
12.如图①是一个斜角坐标系,水平放置的轴称为横轴(记作a轴),斜向放置的轴称为斜轴(记作b轴).类似于直角坐标系,对于斜角坐标平面内的任意一点P,过点P分别作b轴、a轴的平行线交a轴、b轴于点M,N,若点M,N分别在a轴、b轴上所对应的实数为m与n,则称有序实数对(m,n)为点P的坐标.如图②,三角形ABC中,A(1,4),C(3,5),如果平移三角形ABC得到三角形A′B′C′,使点A′与点C重合,在三角形ABC内部,有一任意点D(x,y),则平移后点D的对应点D′的坐标为________________.
【答案】(x+2,y+1)
三、解答题
13.如图,三角形ABC的顶点坐标分别为A(-2,3),B(-3,0),C(-1,-1).将三角形ABC平移后得到三角形A′B′C′,且点A的对应点是A′(2,3),点B,C的对应点分别是B′,C′.
(1)点A,A′之间的距离是 ;
(2)请在图中画出三角形A′B′C′.
解:(1)4
(2)如图所示,三角形A′B′C′即为所求.
14.如图,已知坐标平面内的三个点A(1,3),B(3,1),O(0,0).
(1)平移三角形ABO至三角形A1B1O1,当点A1和点B重合时,求点O1的坐标;
(2)平移三角形ABO至三角形A2B2O2,需要至少向下平移超过 单位,并且至少向左平移超过
个单位,才能使三角形A2B2O2位于第三象限.
解:(1)点O1的坐标为(2,-2).
(2)3 3
15.在平面直角坐标系中,三角形A′B′C′是由三角形ABC平移后得到的,已知三角形ABC内部的一点P(x0,y0)经平移后的对应点为P′(x0+5,y0-2).
(1)三角形A′B′C′是由三角形ABC如何平移得到的?
(2)若已知A(-1,2),B(-4,5),C(-3,0),请写出A′,B′,C′的坐标;
(3)在(2)的条件下,求三角形A′B′C′的面积.
解:(1)三角形ABC先向右平移5个单位长度,再向下平移2个单位长度(或先向下平移2个单位长度,再向右平移5个单位长度)得到三角形A′B′C′.
(2)A′(4,0),B′(1,3),C′(2,-2).
(3)将三角形A′B′C′补成如图所示的长方形,则S三角形A′B′C′=3×5-×5×1-×2×2-×3×3=6.
16.如图,第一象限内有两点P(m-3,n),Q(m,n-2),将线段PQ平移,使点P,Q分别落在两条坐标轴上,求点P平移后的对应点的坐标.
解:设平移后点P,Q的对应点分别是P′,Q′.分两种情况:
①P′在y轴上,Q′在x轴上,则P′的横坐标为0,Q′的纵坐标为0.∵0-(n-2)=-n+2,∴n-n+2=2.∴点P平移后的对应点的坐标是(0,2).
②P′在x轴上,Q′在y轴上,则P′的纵坐标为0,Q′的横坐标为0.∵0-m=-m,∴m-3-m=-3.∴点P平移后的对应点的坐标是(-3,0).综上可知,点P平移后的对应点的坐标是(0,2)或(-3,0).
17.如图,在平面直角坐标系中,A(1,4),B(3,2),O为坐标原点,且OC∥AB,OC=AB.试用平移的知识求C点的坐标,并求四边形ABCO的面积.
解:∵把A点向左平移1个单位长度,再向下平移4个单位长度可得到原点O(0,0),又∵OC∥AB,OC=AB,∴OC可由AB向左平移1个单位长度,再向下平移4个单位长度得到.
∴点B(3,2)向左平移1个单位长度,再向下平移4个单位长度得到点C(2,-2).分别过A,C作x轴的平行线,过B作y轴的平行线,交点为D,E,F,G,如图所示.S四边形ABCO=S长方形DEFG-S三角形AOD-S三角形COE-S三角形BCF-S三角形ABG=3×6-×1×4-×2×2-×1×4-×2×2=10.
一、选择题
1.在平面直角坐标系中,将点(1,1)向右平移2个单位后,得到的点的坐标是( )
A.(3,1) B.(-1,1) C.(1,3) D.(1,-1)
2.在平面直角坐标系中,将点P(-3,2)向下平移4个单位得到点P′,则点P′所在的象限为( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.在平面直角坐标系中,将点A(1,-2)向上平移3个单位长度,再向左平移2个单位长度,得到点B,则点B的坐标是( )
A.(-1,1) B.(3,1) C.(4,-4) D.(4,0)
4.如图,把三角形ABC先向右平移3个单位,再向上平移2个单位得到三角形DEF,则顶点C(0,-1)的对应点坐标为( )
A.(0,0) B.(1,2) C.(1,3) D.(3,1)
5.如图,点A(2,1),将线段OA先向上平移2个单位长度,再向左平移3个单位长度,得到线段O′A′,则点A的对应点A′的坐标是( )
A.(-3,2) B.(0,4) C.(-1,3) D.(3,-1)
6.如图,在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(0,1),将线段AB平移,使其一个端点到C(3,2),则平移后另一端点的坐标为( )
A.(1,3) B.(5,1) C.(1,3)或(3,5) D.(1,3)或(5,1)
7.如图,已知一个直角三角板的直角顶点与原点重合,另两个顶点A,B的坐标分别为(-1,0),(0,).现将该三角板向右平移使点A与点O重合,得到三角形OCB′,则点B的对应点B′的坐标是( )
A.(1,0) B.(,) C.(1,) D.(-1,)
二、填空题
8.点N(-1,3)可以看作由点M(-1,-1)向 平移 个单位所得到的.
9.已知点M(3a-9,1-a),将点M向左平移3个单位长度后落在y轴上,则a= .
10.如图,三角形OAB的顶点A,B的坐标分别为(3,5),(4,0),把三角形OAB沿x轴向右平移得到三角形CDE.如果CB=1,那么点D的坐标为 .
11.如图,在平面直角坐标系中,把一个点从原点开始向上平移1个单位,再向右平移1个单位,得到点A1(1,1);把点A1向上平移2个单位,再向左平移2个单位,得到点A2(-1,3);把点A2向下平移3个单位,再向左平移3个单位,得到点A3(-4,0);把点A3向下平移4个单位,再向右平移4个单位,得到点A4(0,-4)……按此做法进行下去,则点A10的坐标为 .
12.如图①是一个斜角坐标系,水平放置的轴称为横轴(记作a轴),斜向放置的轴称为斜轴(记作b轴).类似于直角坐标系,对于斜角坐标平面内的任意一点P,过点P分别作b轴、a轴的平行线交a轴、b轴于点M,N,若点M,N分别在a轴、b轴上所对应的实数为m与n,则称有序实数对(m,n)为点P的坐标.如图②,三角形ABC中,A(1,4),C(3,5),如果平移三角形ABC得到三角形A′B′C′,使点A′与点C重合,在三角形ABC内部,有一任意点D(x,y),则平移后点D的对应点D′的坐标为________________.
三、解答题
13.如图,三角形ABC的顶点坐标分别为A(-2,3),B(-3,0),C(-1,-1).将三角形ABC平移后得到三角形A′B′C′,且点A的对应点是A′(2,3),点B,C的对应点分别是B′,C′.
(1)点A,A′之间的距离是 ;
(2)请在图中画出三角形A′B′C′.
14.如图,已知坐标平面内的三个点A(1,3),B(3,1),O(0,0).
(1)平移三角形ABO至三角形A1B1O1,当点A1和点B重合时,求点O1的坐标;
(2)平移三角形ABO至三角形A2B2O2,需要至少向下平移超过 单位,并且至少向左平移超过
个单位,才能使三角形A2B2O2位于第三象限.
15.在平面直角坐标系中,三角形A′B′C′是由三角形ABC平移后得到的,已知三角形ABC内部的一点P(x0,y0)经平移后的对应点为P′(x0+5,y0-2).
(1)三角形A′B′C′是由三角形ABC如何平移得到的?
(2)若已知A(-1,2),B(-4,5),C(-3,0),请写出A′,B′,C′的坐标;
(3)在(2)的条件下,求三角形A′B′C′的面积.
16.如图,第一象限内有两点P(m-3,n),Q(m,n-2),将线段PQ平移,使点P,Q分别落在两条坐标轴上,求点P平移后的对应点的坐标.
17.如图,在平面直角坐标系中,A(1,4),B(3,2),O为坐标原点,且OC∥AB,OC=AB.试用平移的知识求C点的坐标,并求四边形ABCO的面积.
参考答案
一、选择题
1.在平面直角坐标系中,将点(1,1)向右平移2个单位后,得到的点的坐标是( A )
A.(3,1) B.(-1,1) C.(1,3) D.(1,-1)
2.在平面直角坐标系中,将点P(-3,2)向下平移4个单位得到点P′,则点P′所在的象限为( C )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.在平面直角坐标系中,将点A(1,-2)向上平移3个单位长度,再向左平移2个单位长度,得到点B,则点B的坐标是( A )
A.(-1,1) B.(3,1) C.(4,-4) D.(4,0)
4.如图,把三角形ABC先向右平移3个单位,再向上平移2个单位得到三角形DEF,则顶点C(0,-1)的对应点坐标为( D )
A.(0,0) B.(1,2) C.(1,3) D.(3,1)
5.如图,点A(2,1),将线段OA先向上平移2个单位长度,再向左平移3个单位长度,得到线段O′A′,则点A的对应点A′的坐标是( C )
A.(-3,2) B.(0,4) C.(-1,3) D.(3,-1)
6.如图,在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(0,1),将线段AB平移,使其一个端点到C(3,2),则平移后另一端点的坐标为( D )
A.(1,3) B.(5,1) C.(1,3)或(3,5) D.(1,3)或(5,1)
7.如图,已知一个直角三角板的直角顶点与原点重合,另两个顶点A,B的坐标分别为(-1,0),(0,).现将该三角板向右平移使点A与点O重合,得到三角形OCB′,则点B的对应点B′的坐标是( C )
A.(1,0) B.(,) C.(1,) D.(-1,)
二、填空题
8.点N(-1,3)可以看作由点M(-1,-1)向 平移 个单位所得到的.
【答案】上 4
9.已知点M(3a-9,1-a),将点M向左平移3个单位长度后落在y轴上,则a= .
【答案】4
10.如图,三角形OAB的顶点A,B的坐标分别为(3,5),(4,0),把三角形OAB沿x轴向右平移得到三角形CDE.如果CB=1,那么点D的坐标为 .
【答案】(6,5)
11.如图,在平面直角坐标系中,把一个点从原点开始向上平移1个单位,再向右平移1个单位,得到点A1(1,1);把点A1向上平移2个单位,再向左平移2个单位,得到点A2(-1,3);把点A2向下平移3个单位,再向左平移3个单位,得到点A3(-4,0);把点A3向下平移4个单位,再向右平移4个单位,得到点A4(0,-4)……按此做法进行下去,则点A10的坐标为 .
【答案】(-1,11)
12.如图①是一个斜角坐标系,水平放置的轴称为横轴(记作a轴),斜向放置的轴称为斜轴(记作b轴).类似于直角坐标系,对于斜角坐标平面内的任意一点P,过点P分别作b轴、a轴的平行线交a轴、b轴于点M,N,若点M,N分别在a轴、b轴上所对应的实数为m与n,则称有序实数对(m,n)为点P的坐标.如图②,三角形ABC中,A(1,4),C(3,5),如果平移三角形ABC得到三角形A′B′C′,使点A′与点C重合,在三角形ABC内部,有一任意点D(x,y),则平移后点D的对应点D′的坐标为________________.
【答案】(x+2,y+1)
三、解答题
13.如图,三角形ABC的顶点坐标分别为A(-2,3),B(-3,0),C(-1,-1).将三角形ABC平移后得到三角形A′B′C′,且点A的对应点是A′(2,3),点B,C的对应点分别是B′,C′.
(1)点A,A′之间的距离是 ;
(2)请在图中画出三角形A′B′C′.
解:(1)4
(2)如图所示,三角形A′B′C′即为所求.
14.如图,已知坐标平面内的三个点A(1,3),B(3,1),O(0,0).
(1)平移三角形ABO至三角形A1B1O1,当点A1和点B重合时,求点O1的坐标;
(2)平移三角形ABO至三角形A2B2O2,需要至少向下平移超过 单位,并且至少向左平移超过
个单位,才能使三角形A2B2O2位于第三象限.
解:(1)点O1的坐标为(2,-2).
(2)3 3
15.在平面直角坐标系中,三角形A′B′C′是由三角形ABC平移后得到的,已知三角形ABC内部的一点P(x0,y0)经平移后的对应点为P′(x0+5,y0-2).
(1)三角形A′B′C′是由三角形ABC如何平移得到的?
(2)若已知A(-1,2),B(-4,5),C(-3,0),请写出A′,B′,C′的坐标;
(3)在(2)的条件下,求三角形A′B′C′的面积.
解:(1)三角形ABC先向右平移5个单位长度,再向下平移2个单位长度(或先向下平移2个单位长度,再向右平移5个单位长度)得到三角形A′B′C′.
(2)A′(4,0),B′(1,3),C′(2,-2).
(3)将三角形A′B′C′补成如图所示的长方形,则S三角形A′B′C′=3×5-×5×1-×2×2-×3×3=6.
16.如图,第一象限内有两点P(m-3,n),Q(m,n-2),将线段PQ平移,使点P,Q分别落在两条坐标轴上,求点P平移后的对应点的坐标.
解:设平移后点P,Q的对应点分别是P′,Q′.分两种情况:
①P′在y轴上,Q′在x轴上,则P′的横坐标为0,Q′的纵坐标为0.∵0-(n-2)=-n+2,∴n-n+2=2.∴点P平移后的对应点的坐标是(0,2).
②P′在x轴上,Q′在y轴上,则P′的纵坐标为0,Q′的横坐标为0.∵0-m=-m,∴m-3-m=-3.∴点P平移后的对应点的坐标是(-3,0).综上可知,点P平移后的对应点的坐标是(0,2)或(-3,0).
17.如图,在平面直角坐标系中,A(1,4),B(3,2),O为坐标原点,且OC∥AB,OC=AB.试用平移的知识求C点的坐标,并求四边形ABCO的面积.
解:∵把A点向左平移1个单位长度,再向下平移4个单位长度可得到原点O(0,0),又∵OC∥AB,OC=AB,∴OC可由AB向左平移1个单位长度,再向下平移4个单位长度得到.
∴点B(3,2)向左平移1个单位长度,再向下平移4个单位长度得到点C(2,-2).分别过A,C作x轴的平行线,过B作y轴的平行线,交点为D,E,F,G,如图所示.S四边形ABCO=S长方形DEFG-S三角形AOD-S三角形COE-S三角形BCF-S三角形ABG=3×6-×1×4-×2×2-×1×4-×2×2=10.
