20.2数据的集中趋势与离散程度(2)课件(共25张PPT)
文档属性
| 名称 | 20.2数据的集中趋势与离散程度(2)课件(共25张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 726.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-06 00:00:00 | ||
图片预览





文档简介
(共25张PPT)
20.2数据的集中趋势与离散程度(2)
数据的集中趋势
加权平均数
教学目标:
1.理解加权平均数的意义;
2.会用加权平均数分析一组数据的集中趋势,发展
数据分析能力,逐步形成数据分析观念.
3.会用计算器求加权平均数.
教学重点:
会根据频数分布计算加权平均数,体会权的意义.
教学难点:
根据频数分布求加权平均数的近似值.
阅读教材 P119~120,完成下列问题:
什么是加权平均数
平均数的计算公式如何表示?
自我学习,生成能力
在求 n 个数的算术平均数时,如果 x1 出现 f1 次, x2出现 f2 次,…,xk 出现 fk 次(这里 f1 + f2 +…+ fk = n ),那么这 n 个数的平均数
叫做 x1 ,x2 ,…,xk 这 k个数的加权平均数,其中f1 ,f2 ,…,fk 分别叫做x1 ,x2 ,…,xk 的权.
X
=
x1f1+x2f2+ … +xkfk
f1+f2+ … +fk
权的本义是秤砣
f1+f2+ … +fk
=n
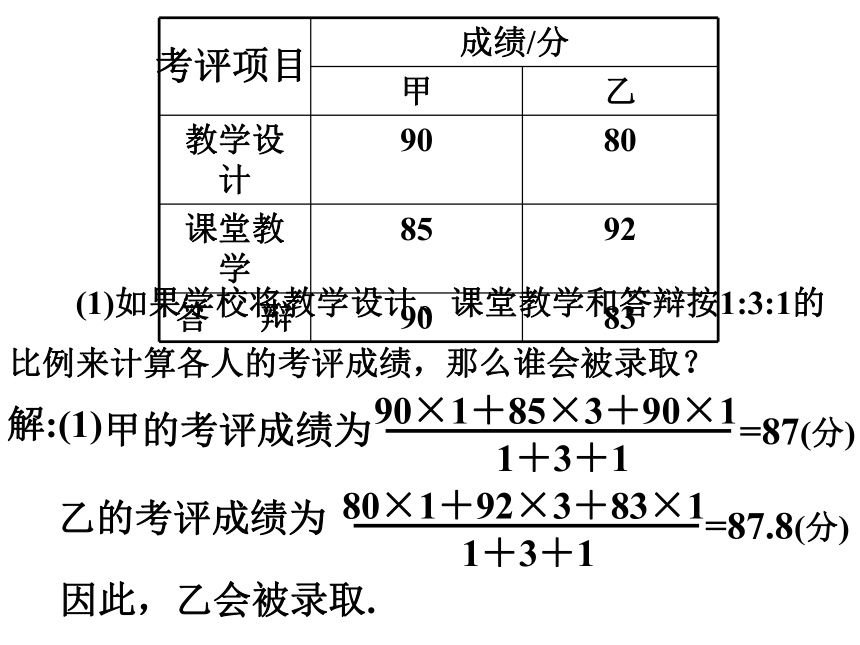
例2 某校在招聘教师时以考评成绩确定人选.
甲、乙两位高校毕业生的各项考评成绩如下表:
成绩/分
甲 乙
教学设计 90 80
课堂教学 85 92
答 辩 90 83
考评项目
(1)如果学校将教学设计、课堂教学和答辩按
1:3:1的比例来计算各人的考评成绩,那么谁会被录取?
典型例析
成绩/分
甲 乙
教学设计 90 80
课堂教学 85 92
答 辩 90 83
考评项目
(1)如果学校将教学设计、课堂教学和答辩按1:3:1的
比例来计算各人的考评成绩,那么谁会被录取?
甲的考评成绩为
乙的考评成绩为
解:(1)
90×1+85×3+90×1
1+3+1
=87(分)
80×1+92×3+83×1
1+3+1
=87.8(分)
因此,乙会被录取.
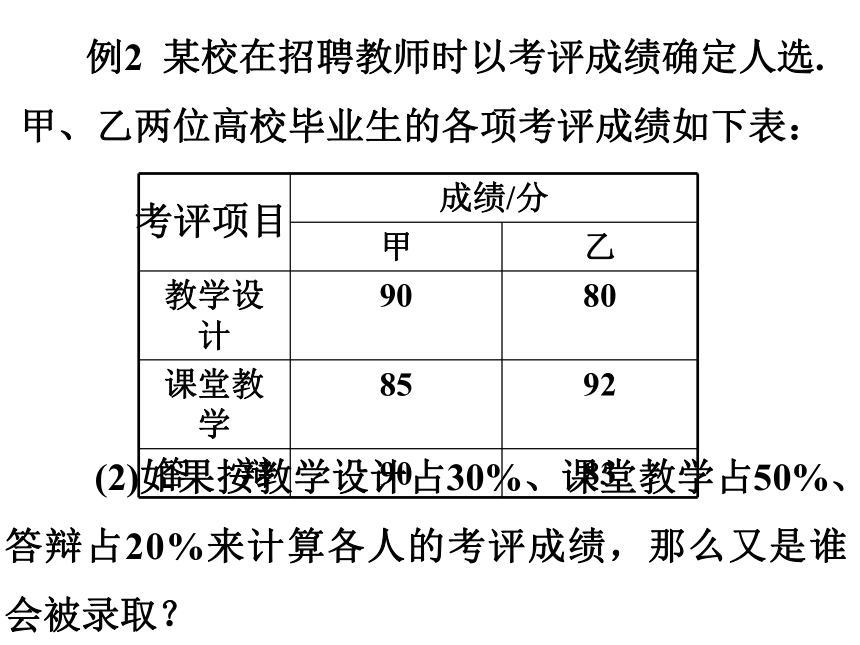
例2 某校在招聘教师时以考评成绩确定人选.
甲、乙两位高校毕业生的各项考评成绩如下表:
成绩/分
甲 乙
教学设计 90 80
课堂教学 85 92
答 辩 90 83
考评项目
(2)如果按教学设计占30%、课堂教学占50%、答辩占20%来计算各人的考评成绩,那么又是谁会被录取?
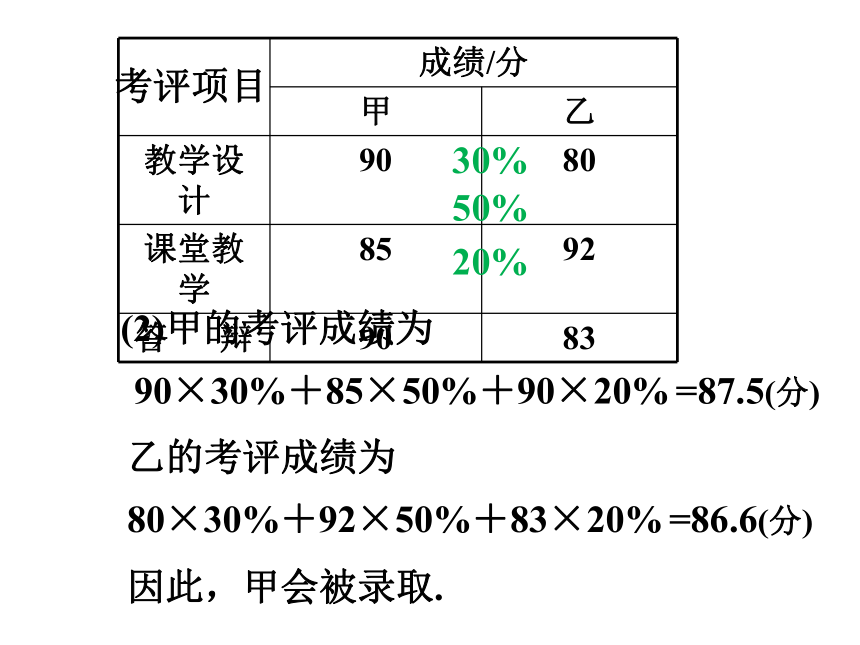
成绩/分
甲 乙
教学设计 90 80
课堂教学 85 92
答 辩 90 83
考评项目
(2)甲的考评成绩为
30%
50%
20%
90×30%+85×50%+90×20%
=87.5(分)
乙的考评成绩为
80×30%+92×50%+83×20%
=86.6(分)
因此,甲会被录取.
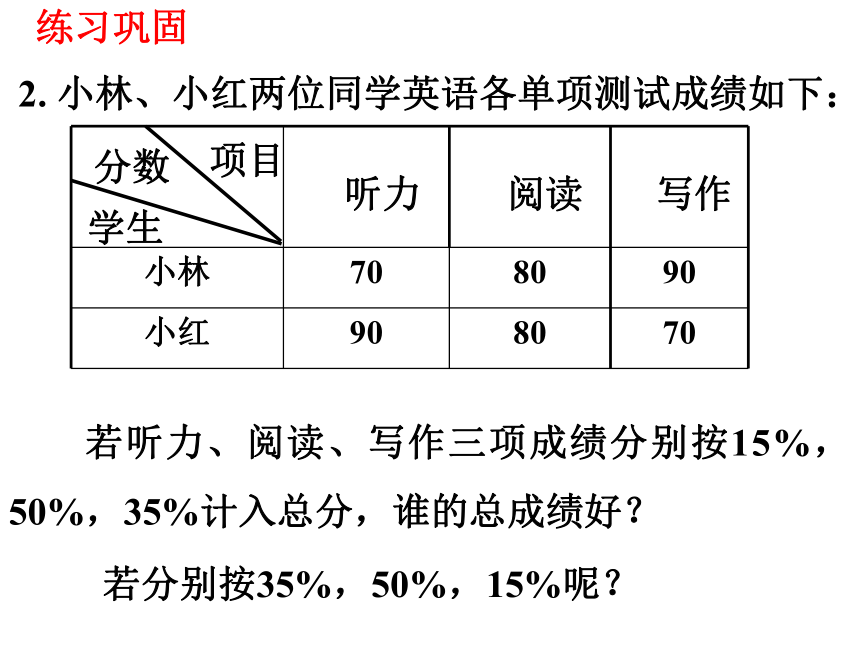
2. 小林、小红两位同学英语各单项测试成绩如下:
小林 70 80 90
小红 90 80 70
若听力、阅读、写作三项成绩分别按15%,50%,35%计入总分,谁的总成绩好?
学生
分数
项目
听力
阅读
写作
若分别按35%,50%,15%呢?
练习巩固
小林 70 80 90
小红 90 80 70
学生
分数
项目
听力
阅读
写作
解:
小林的总成绩为
70×15%+80×50%+90×35%
=82(分)
15%
50%
35%
小红的总成绩为
90×15%+80×50%+70×35%
=78(分)
此时,小林的成绩好.
小林 70 80 90
小红 90 80 70
学生
分数
项目
听力
阅读
写作
解:
小林的总成绩为
70×35%+80×50%+90×15%
=78(分)
35%
50%
15%
小红的总成绩为
90×35%+80×50%+70×15%
=82(分)
此时,小红的成绩好.
请同学们阅读课本122页,阅读后探究下列问题.
(1)如何利用计算器求一组数据的平均数吗?
(2)一组数据中的相同数据怎样输入?
(3) 按错了键怎么办?输错了数据呢?
(4)如何求一组数据的和?
认识计算器
下面我们以P118例1为例求选手甲的平均分说明计算器操作步骤:
1. 开机;
2. 清除原有数据;
3. 1,选择单变量统计模式;
4. 9.0 ,输入数据9.0(显示n=1为样
本数,下同);
5. ,重复输入数据9.0;
ON/C
2ndf
DEL
MODE
2ndf
DATA
DATA
下面我们以P118的例1求选手甲的平均分说明计算器操作步骤:
6. 9.2 3 ,输入3个相同的数据9.2;
7. 9.8 ,输入数据9.8;
8. 8.8 ,输入数据8.8;
9. 9.5 ,输入数据9.5;
10. ,计算这组数据的平均数。
,
RCL
DATA
DATA
DATA
DATA
RCL
DATA
Σx
如何求一组数据的和
按
键即可。
输错了数据怎么办?
在按前
键前出现输入错误,
只要按
ON/C
键即可删除;
DATA
在按前
键后出现输入错误,
需用
键确认最后输入的数据,
按
键清除。
2ndf
CD
(1) 利用计算器计算下列数据的平均数:
12.8,12.9,13.4,13.0,14.1,13.5,12.7,12.4,13.9,13.8,14.3,13.2,13.5.
练习巩固
解:
X ≈
13.35.
(2)某校七年级数学竞赛中,为了了解甲、乙两
班学生竞赛的情况,从每班抽取十个学生的
成绩进行分析:(单位:分) 甲:86 78 86 92 85 87 86 88 80 84 乙:78 94 87 82 81 86 76 87 85 80 用科学计算器分别计算他们的成绩的平均数,并根据计算结果说明哪个班的成绩较好?
解:
X甲=
X乙=
85.2,
84;
甲班的成绩较好.
(3)为了解用电量的多少,李明同学在六月初
连续几天同一时刻观察电表显示的度数,
记录如下:
估计李明家六月份的总电量是________度。
日期 1 2 3 4 5 6 7 8
示数/度 117 120 124 129 135 138 142 145
131.23
1.什么是加权平均数
2.平均数的计算公式如何表示?
课堂小结
3.如何利用计算器求一组数据的平均数吗?
1.某校随机调查了该校八年级的学生50名, 了解他们在校的体育锻炼时间,记录如下:
则这50名同学这一周在校的平均体育锻炼
时间是______小时.
时间(小时) 5 6 7 8
人数 10 15 20 5
巩固提高
6.4
2.某中学规定:学生的学期体育综合成绩满分为100分,其中,期中考试成绩占40%,期末考试占60%.小军这个学期的期中,期末体育考试分别是80、90分(百分制),则小军这个学期的体育综合成绩是 分.
80
3.某校为了招聘一名优秀教师,对入选的三名候选人进行教学技能与专业知识两种考核,现将甲、乙、丙三人的考核成绩统计如下:
(1) 如果校方认为教师的教学技能水平与专业知识水平同等重要,则候选人 将被录取.
(2) 如果校方认为教师的教学技能水平比专业知识水平重要,因此分别赋予它们6和4的权. 计算他们赋权后各自的平均成绩,并说明谁将被录取.
候选人 百分制
教学技能
考核成绩 专业知识
考核成绩
甲 85 92
乙 91 85
丙 80 90
甲
甲的成绩为
解:(2)
85×6+92×4
6+4
=87.8(分)
这时,乙的成绩最好,被录取会是乙.
乙的成绩为
91×6+85×4
6+4
=88.6(分)
丙的成绩为
80×6+90×4
6+4
=84(分)
今天作业
课本P115页第1题
20.2数据的集中趋势与离散程度(2)
数据的集中趋势
加权平均数
教学目标:
1.理解加权平均数的意义;
2.会用加权平均数分析一组数据的集中趋势,发展
数据分析能力,逐步形成数据分析观念.
3.会用计算器求加权平均数.
教学重点:
会根据频数分布计算加权平均数,体会权的意义.
教学难点:
根据频数分布求加权平均数的近似值.
阅读教材 P119~120,完成下列问题:
什么是加权平均数
平均数的计算公式如何表示?
自我学习,生成能力
在求 n 个数的算术平均数时,如果 x1 出现 f1 次, x2出现 f2 次,…,xk 出现 fk 次(这里 f1 + f2 +…+ fk = n ),那么这 n 个数的平均数
叫做 x1 ,x2 ,…,xk 这 k个数的加权平均数,其中f1 ,f2 ,…,fk 分别叫做x1 ,x2 ,…,xk 的权.
X
=
x1f1+x2f2+ … +xkfk
f1+f2+ … +fk
权的本义是秤砣
f1+f2+ … +fk
=n
例2 某校在招聘教师时以考评成绩确定人选.
甲、乙两位高校毕业生的各项考评成绩如下表:
成绩/分
甲 乙
教学设计 90 80
课堂教学 85 92
答 辩 90 83
考评项目
(1)如果学校将教学设计、课堂教学和答辩按
1:3:1的比例来计算各人的考评成绩,那么谁会被录取?
典型例析
成绩/分
甲 乙
教学设计 90 80
课堂教学 85 92
答 辩 90 83
考评项目
(1)如果学校将教学设计、课堂教学和答辩按1:3:1的
比例来计算各人的考评成绩,那么谁会被录取?
甲的考评成绩为
乙的考评成绩为
解:(1)
90×1+85×3+90×1
1+3+1
=87(分)
80×1+92×3+83×1
1+3+1
=87.8(分)
因此,乙会被录取.
例2 某校在招聘教师时以考评成绩确定人选.
甲、乙两位高校毕业生的各项考评成绩如下表:
成绩/分
甲 乙
教学设计 90 80
课堂教学 85 92
答 辩 90 83
考评项目
(2)如果按教学设计占30%、课堂教学占50%、答辩占20%来计算各人的考评成绩,那么又是谁会被录取?
成绩/分
甲 乙
教学设计 90 80
课堂教学 85 92
答 辩 90 83
考评项目
(2)甲的考评成绩为
30%
50%
20%
90×30%+85×50%+90×20%
=87.5(分)
乙的考评成绩为
80×30%+92×50%+83×20%
=86.6(分)
因此,甲会被录取.
2. 小林、小红两位同学英语各单项测试成绩如下:
小林 70 80 90
小红 90 80 70
若听力、阅读、写作三项成绩分别按15%,50%,35%计入总分,谁的总成绩好?
学生
分数
项目
听力
阅读
写作
若分别按35%,50%,15%呢?
练习巩固
小林 70 80 90
小红 90 80 70
学生
分数
项目
听力
阅读
写作
解:
小林的总成绩为
70×15%+80×50%+90×35%
=82(分)
15%
50%
35%
小红的总成绩为
90×15%+80×50%+70×35%
=78(分)
此时,小林的成绩好.
小林 70 80 90
小红 90 80 70
学生
分数
项目
听力
阅读
写作
解:
小林的总成绩为
70×35%+80×50%+90×15%
=78(分)
35%
50%
15%
小红的总成绩为
90×35%+80×50%+70×15%
=82(分)
此时,小红的成绩好.
请同学们阅读课本122页,阅读后探究下列问题.
(1)如何利用计算器求一组数据的平均数吗?
(2)一组数据中的相同数据怎样输入?
(3) 按错了键怎么办?输错了数据呢?
(4)如何求一组数据的和?
认识计算器
下面我们以P118例1为例求选手甲的平均分说明计算器操作步骤:
1. 开机;
2. 清除原有数据;
3. 1,选择单变量统计模式;
4. 9.0 ,输入数据9.0(显示n=1为样
本数,下同);
5. ,重复输入数据9.0;
ON/C
2ndf
DEL
MODE
2ndf
DATA
DATA
下面我们以P118的例1求选手甲的平均分说明计算器操作步骤:
6. 9.2 3 ,输入3个相同的数据9.2;
7. 9.8 ,输入数据9.8;
8. 8.8 ,输入数据8.8;
9. 9.5 ,输入数据9.5;
10. ,计算这组数据的平均数。
,
RCL
DATA
DATA
DATA
DATA
RCL
DATA
Σx
如何求一组数据的和
按
键即可。
输错了数据怎么办?
在按前
键前出现输入错误,
只要按
ON/C
键即可删除;
DATA
在按前
键后出现输入错误,
需用
键确认最后输入的数据,
按
键清除。
2ndf
CD
(1) 利用计算器计算下列数据的平均数:
12.8,12.9,13.4,13.0,14.1,13.5,12.7,12.4,13.9,13.8,14.3,13.2,13.5.
练习巩固
解:
X ≈
13.35.
(2)某校七年级数学竞赛中,为了了解甲、乙两
班学生竞赛的情况,从每班抽取十个学生的
成绩进行分析:(单位:分) 甲:86 78 86 92 85 87 86 88 80 84 乙:78 94 87 82 81 86 76 87 85 80 用科学计算器分别计算他们的成绩的平均数,并根据计算结果说明哪个班的成绩较好?
解:
X甲=
X乙=
85.2,
84;
甲班的成绩较好.
(3)为了解用电量的多少,李明同学在六月初
连续几天同一时刻观察电表显示的度数,
记录如下:
估计李明家六月份的总电量是________度。
日期 1 2 3 4 5 6 7 8
示数/度 117 120 124 129 135 138 142 145
131.23
1.什么是加权平均数
2.平均数的计算公式如何表示?
课堂小结
3.如何利用计算器求一组数据的平均数吗?
1.某校随机调查了该校八年级的学生50名, 了解他们在校的体育锻炼时间,记录如下:
则这50名同学这一周在校的平均体育锻炼
时间是______小时.
时间(小时) 5 6 7 8
人数 10 15 20 5
巩固提高
6.4
2.某中学规定:学生的学期体育综合成绩满分为100分,其中,期中考试成绩占40%,期末考试占60%.小军这个学期的期中,期末体育考试分别是80、90分(百分制),则小军这个学期的体育综合成绩是 分.
80
3.某校为了招聘一名优秀教师,对入选的三名候选人进行教学技能与专业知识两种考核,现将甲、乙、丙三人的考核成绩统计如下:
(1) 如果校方认为教师的教学技能水平与专业知识水平同等重要,则候选人 将被录取.
(2) 如果校方认为教师的教学技能水平比专业知识水平重要,因此分别赋予它们6和4的权. 计算他们赋权后各自的平均成绩,并说明谁将被录取.
候选人 百分制
教学技能
考核成绩 专业知识
考核成绩
甲 85 92
乙 91 85
丙 80 90
甲
甲的成绩为
解:(2)
85×6+92×4
6+4
=87.8(分)
这时,乙的成绩最好,被录取会是乙.
乙的成绩为
91×6+85×4
6+4
=88.6(分)
丙的成绩为
80×6+90×4
6+4
=84(分)
今天作业
课本P115页第1题
