人教版七年级下册 8.3.1 利用二元一次方程组解决实际问题 同步练习(含答案)
文档属性
| 名称 | 人教版七年级下册 8.3.1 利用二元一次方程组解决实际问题 同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 167.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-05 00:00:00 | ||
图片预览


文档简介
8.3.1 利用二元一次方程组解决实际问题
一、选择题
1.“六一”儿童节前夕,某超市用3360元购进A,B两种童装共120套,其中A种童装每套24元,B种童装每套36元.若设购A种童装x套,B种童装y套,根据题意列方程组正确的是( )
A. B. C. D.
2. “市长杯”青少年校园足球联赛的比赛规则是:胜一场得3分,平一场得1分,负一场得0分.某校足球队在第一轮比赛中赛了9场,只负了2场,共得17分.那么该队胜了几场,平了几场?设该队胜了x场,平了y场,根据题意可列方程组为( )
A. B. C. D.
3. “五一”小长假,小华和家人到公园游玩.湖边有大小两种游船.小华发现1艘大船与2艘小船一次共可以满载游客32人,2艘大船与1艘小船一次共可以满载游客46人.则1艘大船与1艘小船一次共可以满载游客的人数为( )
A.30 B.26 C.24 D.22
4.有大小两种货车,2辆大货车与3辆小货车一次共可运货15.5吨,5辆大货车与6辆小货车一次共可运货35吨,则每辆小货车一次可运货( )
A.2吨 B.2.5吨 C.3吨 D.3.5吨
5.幻方是古老的数学问题,我国古代的《洛书》中记载了最早的幻方——九宫格.将9个数填入幻方的空格中,要求每一横行、每一竖列以及两条对角线上的3个数之和相等.如图是一个未完成的幻方,则x与y的和是( )
A.9 B.10 C.11 D.12
二、填空题
6.小强同学生日的月数减去日数为2,月数的两倍和日数相加为31,则小强同学生日的月数和日数的和为 .
7.一长方形的周长是44 cm,若宽的3倍比长多6 cm,则该长方形的面积是 cm2.
8.甲种电影票每张20元,乙种电影票每张15元.若购买甲、乙两种电影票共40张,恰好用去700元,则甲种电影票买了 张.
9.欣欣超市为促销,决定对A,B两种商品统一进行打8折销售,打折前,买6件A商品和3件B商品需要54元,买3件A商品和4件B商品需要32元,打折后,小敏买50件A商品和40件B商品仅需 元.
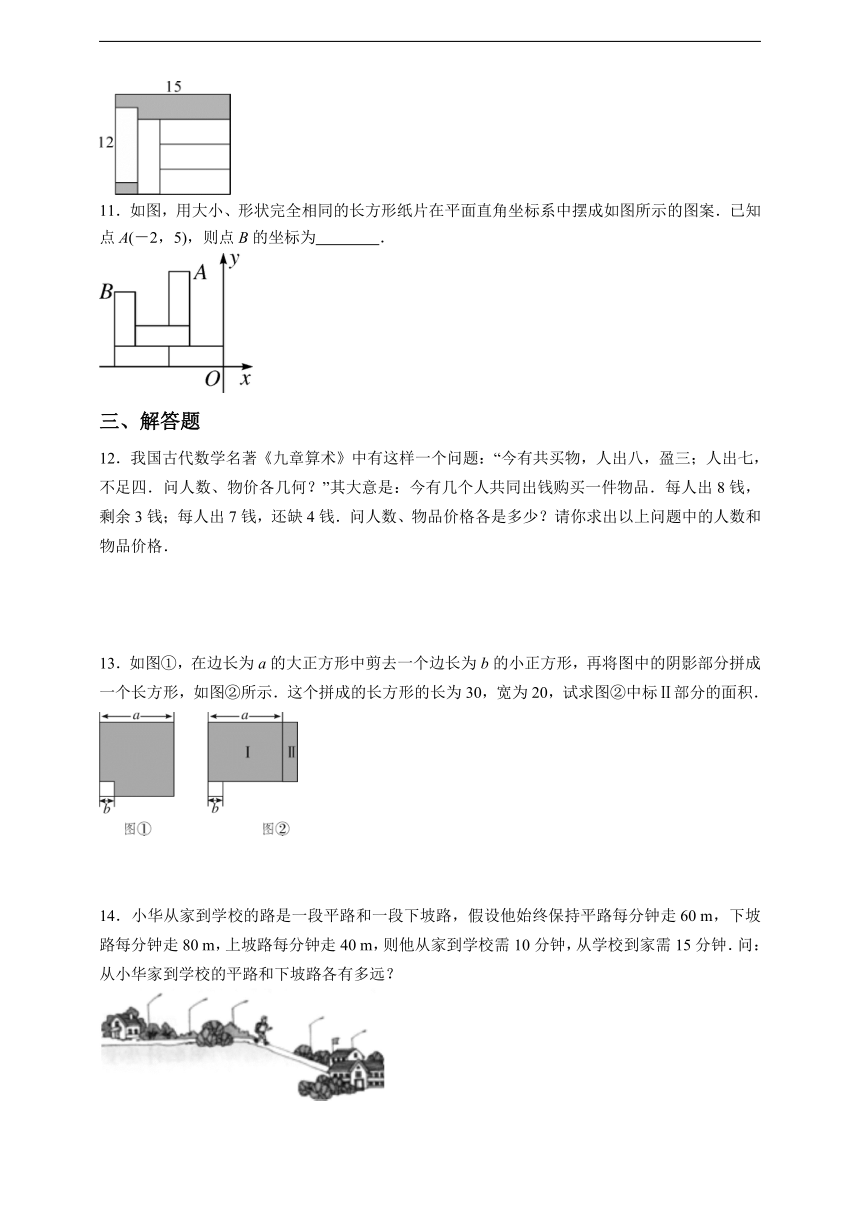
10.如图,在长为15、宽为12的长方形中,有形状、大小完全相同的5个小长方形,则图中阴影部分的面积为 .
11.如图,用大小、形状完全相同的长方形纸片在平面直角坐标系中摆成如图所示的图案.已知点A(-2,5),则点B的坐标为 .
三、解答题
12.我国古代数学名著《九章算术》中有这样一个问题:“今有共买物,人出八,盈三;人出七,不足四.问人数、物价各几何?”其大意是:今有几个人共同出钱购买一件物品.每人出8钱,剩余3钱;每人出7钱,还缺4钱.问人数、物品价格各是多少?请你求出以上问题中的人数和物品价格.
13.如图①,在边长为a的大正方形中剪去一个边长为b的小正方形,再将图中的阴影部分拼成一个长方形,如图②所示.这个拼成的长方形的长为30,宽为20,试求图②中标Ⅱ部分的面积.
14.小华从家到学校的路是一段平路和一段下坡路,假设他始终保持平路每分钟走60 m,下坡路每分钟走80 m,上坡路每分钟走40 m,则他从家到学校需10分钟,从学校到家需15分钟.问:从小华家到学校的平路和下坡路各有多远?
15.本地某快递公司规定:寄件不超过1千克的部分按起步价计费,寄件超过1千克的部分按千克计费.小丽分别寄快递到上海和北京,收费标准及实际收费如下表:
收费标准:
目的地 起步价(元) 超过1千克的部分(元/千克)
上海 a b
北京 a+3 b+4
实际收费:
目的地 质量(千克) 费用(元)
上海 2 9
北京 3 22
求a,b的值.
16.某大型运动会召开期间,大批的大学生志愿者参与服务工作.某大学计划组织本校全体志愿者统一乘车去会场,若单独调配36座新能源客车若干辆,则有2人没有座位;若只调配22座新能源客车,则用车数量将增加4辆,并空出2个座位.
(1)计划调配36座新能源客车多少辆?该大学共有多少名志愿者?
(2)若同时调配36座和22座两种车型,既保证每人有座,又保证每车不空座,则两种车型各需多少辆?
参考答案
一、选择题
1.“六一”儿童节前夕,某超市用3360元购进A,B两种童装共120套,其中A种童装每套24元,B种童装每套36元.若设购A种童装x套,B种童装y套,根据题意列方程组正确的是( B )
A. B. C. D.
2. “市长杯”青少年校园足球联赛的比赛规则是:胜一场得3分,平一场得1分,负一场得0分.某校足球队在第一轮比赛中赛了9场,只负了2场,共得17分.那么该队胜了几场,平了几场?设该队胜了x场,平了y场,根据题意可列方程组为( A )
A. B. C. D.
3. “五一”小长假,小华和家人到公园游玩.湖边有大小两种游船.小华发现1艘大船与2艘小船一次共可以满载游客32人,2艘大船与1艘小船一次共可以满载游客46人.则1艘大船与1艘小船一次共可以满载游客的人数为( B )
A.30 B.26 C.24 D.22
4.有大小两种货车,2辆大货车与3辆小货车一次共可运货15.5吨,5辆大货车与6辆小货车一次共可运货35吨,则每辆小货车一次可运货( B )
A.2吨 B.2.5吨 C.3吨 D.3.5吨
5.幻方是古老的数学问题,我国古代的《洛书》中记载了最早的幻方——九宫格.将9个数填入幻方的空格中,要求每一横行、每一竖列以及两条对角线上的3个数之和相等.如图是一个未完成的幻方,则x与y的和是( D )
A.9 B.10 C.11 D.12
二、填空题
6.小强同学生日的月数减去日数为2,月数的两倍和日数相加为31,则小强同学生日的月数和日数的和为 .
【答案】20
7.一长方形的周长是44 cm,若宽的3倍比长多6 cm,则该长方形的面积是 cm2.
【答案】105
8.甲种电影票每张20元,乙种电影票每张15元.若购买甲、乙两种电影票共40张,恰好用去700元,则甲种电影票买了 张.
【答案】20
9.欣欣超市为促销,决定对A,B两种商品统一进行打8折销售,打折前,买6件A商品和3件B商品需要54元,买3件A商品和4件B商品需要32元,打折后,小敏买50件A商品和40件B商品仅需 元.
【答案】384
10.如图,在长为15、宽为12的长方形中,有形状、大小完全相同的5个小长方形,则图中阴影部分的面积为 .
【答案】45
11.如图,用大小、形状完全相同的长方形纸片在平面直角坐标系中摆成如图所示的图案.已知点A(-2,5),则点B的坐标为 .
【答案】(-6,4)
三、解答题
12.我国古代数学名著《九章算术》中有这样一个问题:“今有共买物,人出八,盈三;人出七,不足四.问人数、物价各几何?”其大意是:今有几个人共同出钱购买一件物品.每人出8钱,剩余3钱;每人出7钱,还缺4钱.问人数、物品价格各是多少?请你求出以上问题中的人数和物品价格.
解:设有x个人,物品的价格为y钱,
由题意得解得
答:有7个人,物品的价格为53钱.
13.如图①,在边长为a的大正方形中剪去一个边长为b的小正方形,再将图中的阴影部分拼成一个长方形,如图②所示.这个拼成的长方形的长为30,宽为20,试求图②中标Ⅱ部分的面积.
解:由题意及图可得解得
所以标Ⅱ部分的面积为b(a-b)=5×(25-5)=100.
14.小华从家到学校的路是一段平路和一段下坡路,假设他始终保持平路每分钟走60 m,下坡路每分钟走80 m,上坡路每分钟走40 m,则他从家到学校需10分钟,从学校到家需15分钟.问:从小华家到学校的平路和下坡路各有多远?
解:设从小华家到学校的平路有x m,下坡路有y m.根据题意得解得
答:从小华家到学校的平路和下坡路分别为300 m,400 m.
15.本地某快递公司规定:寄件不超过1千克的部分按起步价计费,寄件超过1千克的部分按千克计费.小丽分别寄快递到上海和北京,收费标准及实际收费如下表:
收费标准:
目的地 起步价(元) 超过1千克的部分(元/千克)
上海 a b
北京 a+3 b+4
实际收费:
目的地 质量(千克) 费用(元)
上海 2 9
北京 3 22
求a,b的值.
解:依题意,得
解得答:a的值为7,b的值为2.
16.某大型运动会召开期间,大批的大学生志愿者参与服务工作.某大学计划组织本校全体志愿者统一乘车去会场,若单独调配36座新能源客车若干辆,则有2人没有座位;若只调配22座新能源客车,则用车数量将增加4辆,并空出2个座位.
(1)计划调配36座新能源客车多少辆?该大学共有多少名志愿者?
解:设计划调配36座新能源客车x辆,该大学共有y名志愿者,则需调配22座新能源客车(x+4)辆.
依题意,得解得
答:计划调配36座新能源客车6辆,该大学共有218名志愿者.
(2)若同时调配36座和22座两种车型,既保证每人有座,又保证每车不空座,则两种车型各需多少辆?
解:设需调配36座客车m辆,22座客车n辆,
依题意,得36m+22n=218,∴n=.
又∵m,n均为正整数,∴
答:需调配36座客车3辆,22座客车5辆.
一、选择题
1.“六一”儿童节前夕,某超市用3360元购进A,B两种童装共120套,其中A种童装每套24元,B种童装每套36元.若设购A种童装x套,B种童装y套,根据题意列方程组正确的是( )
A. B. C. D.
2. “市长杯”青少年校园足球联赛的比赛规则是:胜一场得3分,平一场得1分,负一场得0分.某校足球队在第一轮比赛中赛了9场,只负了2场,共得17分.那么该队胜了几场,平了几场?设该队胜了x场,平了y场,根据题意可列方程组为( )
A. B. C. D.
3. “五一”小长假,小华和家人到公园游玩.湖边有大小两种游船.小华发现1艘大船与2艘小船一次共可以满载游客32人,2艘大船与1艘小船一次共可以满载游客46人.则1艘大船与1艘小船一次共可以满载游客的人数为( )
A.30 B.26 C.24 D.22
4.有大小两种货车,2辆大货车与3辆小货车一次共可运货15.5吨,5辆大货车与6辆小货车一次共可运货35吨,则每辆小货车一次可运货( )
A.2吨 B.2.5吨 C.3吨 D.3.5吨
5.幻方是古老的数学问题,我国古代的《洛书》中记载了最早的幻方——九宫格.将9个数填入幻方的空格中,要求每一横行、每一竖列以及两条对角线上的3个数之和相等.如图是一个未完成的幻方,则x与y的和是( )
A.9 B.10 C.11 D.12
二、填空题
6.小强同学生日的月数减去日数为2,月数的两倍和日数相加为31,则小强同学生日的月数和日数的和为 .
7.一长方形的周长是44 cm,若宽的3倍比长多6 cm,则该长方形的面积是 cm2.
8.甲种电影票每张20元,乙种电影票每张15元.若购买甲、乙两种电影票共40张,恰好用去700元,则甲种电影票买了 张.
9.欣欣超市为促销,决定对A,B两种商品统一进行打8折销售,打折前,买6件A商品和3件B商品需要54元,买3件A商品和4件B商品需要32元,打折后,小敏买50件A商品和40件B商品仅需 元.
10.如图,在长为15、宽为12的长方形中,有形状、大小完全相同的5个小长方形,则图中阴影部分的面积为 .
11.如图,用大小、形状完全相同的长方形纸片在平面直角坐标系中摆成如图所示的图案.已知点A(-2,5),则点B的坐标为 .
三、解答题
12.我国古代数学名著《九章算术》中有这样一个问题:“今有共买物,人出八,盈三;人出七,不足四.问人数、物价各几何?”其大意是:今有几个人共同出钱购买一件物品.每人出8钱,剩余3钱;每人出7钱,还缺4钱.问人数、物品价格各是多少?请你求出以上问题中的人数和物品价格.
13.如图①,在边长为a的大正方形中剪去一个边长为b的小正方形,再将图中的阴影部分拼成一个长方形,如图②所示.这个拼成的长方形的长为30,宽为20,试求图②中标Ⅱ部分的面积.
14.小华从家到学校的路是一段平路和一段下坡路,假设他始终保持平路每分钟走60 m,下坡路每分钟走80 m,上坡路每分钟走40 m,则他从家到学校需10分钟,从学校到家需15分钟.问:从小华家到学校的平路和下坡路各有多远?
15.本地某快递公司规定:寄件不超过1千克的部分按起步价计费,寄件超过1千克的部分按千克计费.小丽分别寄快递到上海和北京,收费标准及实际收费如下表:
收费标准:
目的地 起步价(元) 超过1千克的部分(元/千克)
上海 a b
北京 a+3 b+4
实际收费:
目的地 质量(千克) 费用(元)
上海 2 9
北京 3 22
求a,b的值.
16.某大型运动会召开期间,大批的大学生志愿者参与服务工作.某大学计划组织本校全体志愿者统一乘车去会场,若单独调配36座新能源客车若干辆,则有2人没有座位;若只调配22座新能源客车,则用车数量将增加4辆,并空出2个座位.
(1)计划调配36座新能源客车多少辆?该大学共有多少名志愿者?
(2)若同时调配36座和22座两种车型,既保证每人有座,又保证每车不空座,则两种车型各需多少辆?
参考答案
一、选择题
1.“六一”儿童节前夕,某超市用3360元购进A,B两种童装共120套,其中A种童装每套24元,B种童装每套36元.若设购A种童装x套,B种童装y套,根据题意列方程组正确的是( B )
A. B. C. D.
2. “市长杯”青少年校园足球联赛的比赛规则是:胜一场得3分,平一场得1分,负一场得0分.某校足球队在第一轮比赛中赛了9场,只负了2场,共得17分.那么该队胜了几场,平了几场?设该队胜了x场,平了y场,根据题意可列方程组为( A )
A. B. C. D.
3. “五一”小长假,小华和家人到公园游玩.湖边有大小两种游船.小华发现1艘大船与2艘小船一次共可以满载游客32人,2艘大船与1艘小船一次共可以满载游客46人.则1艘大船与1艘小船一次共可以满载游客的人数为( B )
A.30 B.26 C.24 D.22
4.有大小两种货车,2辆大货车与3辆小货车一次共可运货15.5吨,5辆大货车与6辆小货车一次共可运货35吨,则每辆小货车一次可运货( B )
A.2吨 B.2.5吨 C.3吨 D.3.5吨
5.幻方是古老的数学问题,我国古代的《洛书》中记载了最早的幻方——九宫格.将9个数填入幻方的空格中,要求每一横行、每一竖列以及两条对角线上的3个数之和相等.如图是一个未完成的幻方,则x与y的和是( D )
A.9 B.10 C.11 D.12
二、填空题
6.小强同学生日的月数减去日数为2,月数的两倍和日数相加为31,则小强同学生日的月数和日数的和为 .
【答案】20
7.一长方形的周长是44 cm,若宽的3倍比长多6 cm,则该长方形的面积是 cm2.
【答案】105
8.甲种电影票每张20元,乙种电影票每张15元.若购买甲、乙两种电影票共40张,恰好用去700元,则甲种电影票买了 张.
【答案】20
9.欣欣超市为促销,决定对A,B两种商品统一进行打8折销售,打折前,买6件A商品和3件B商品需要54元,买3件A商品和4件B商品需要32元,打折后,小敏买50件A商品和40件B商品仅需 元.
【答案】384
10.如图,在长为15、宽为12的长方形中,有形状、大小完全相同的5个小长方形,则图中阴影部分的面积为 .
【答案】45
11.如图,用大小、形状完全相同的长方形纸片在平面直角坐标系中摆成如图所示的图案.已知点A(-2,5),则点B的坐标为 .
【答案】(-6,4)
三、解答题
12.我国古代数学名著《九章算术》中有这样一个问题:“今有共买物,人出八,盈三;人出七,不足四.问人数、物价各几何?”其大意是:今有几个人共同出钱购买一件物品.每人出8钱,剩余3钱;每人出7钱,还缺4钱.问人数、物品价格各是多少?请你求出以上问题中的人数和物品价格.
解:设有x个人,物品的价格为y钱,
由题意得解得
答:有7个人,物品的价格为53钱.
13.如图①,在边长为a的大正方形中剪去一个边长为b的小正方形,再将图中的阴影部分拼成一个长方形,如图②所示.这个拼成的长方形的长为30,宽为20,试求图②中标Ⅱ部分的面积.
解:由题意及图可得解得
所以标Ⅱ部分的面积为b(a-b)=5×(25-5)=100.
14.小华从家到学校的路是一段平路和一段下坡路,假设他始终保持平路每分钟走60 m,下坡路每分钟走80 m,上坡路每分钟走40 m,则他从家到学校需10分钟,从学校到家需15分钟.问:从小华家到学校的平路和下坡路各有多远?
解:设从小华家到学校的平路有x m,下坡路有y m.根据题意得解得
答:从小华家到学校的平路和下坡路分别为300 m,400 m.
15.本地某快递公司规定:寄件不超过1千克的部分按起步价计费,寄件超过1千克的部分按千克计费.小丽分别寄快递到上海和北京,收费标准及实际收费如下表:
收费标准:
目的地 起步价(元) 超过1千克的部分(元/千克)
上海 a b
北京 a+3 b+4
实际收费:
目的地 质量(千克) 费用(元)
上海 2 9
北京 3 22
求a,b的值.
解:依题意,得
解得答:a的值为7,b的值为2.
16.某大型运动会召开期间,大批的大学生志愿者参与服务工作.某大学计划组织本校全体志愿者统一乘车去会场,若单独调配36座新能源客车若干辆,则有2人没有座位;若只调配22座新能源客车,则用车数量将增加4辆,并空出2个座位.
(1)计划调配36座新能源客车多少辆?该大学共有多少名志愿者?
解:设计划调配36座新能源客车x辆,该大学共有y名志愿者,则需调配22座新能源客车(x+4)辆.
依题意,得解得
答:计划调配36座新能源客车6辆,该大学共有218名志愿者.
(2)若同时调配36座和22座两种车型,既保证每人有座,又保证每车不空座,则两种车型各需多少辆?
解:设需调配36座客车m辆,22座客车n辆,
依题意,得36m+22n=218,∴n=.
又∵m,n均为正整数,∴
答:需调配36座客车3辆,22座客车5辆.
