人教版七年级下册 8.3.2 利用二元一次方程组解决较复杂的问题 同步练习(含答案)
文档属性
| 名称 | 人教版七年级下册 8.3.2 利用二元一次方程组解决较复杂的问题 同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 193.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-05 00:00:00 | ||
图片预览



文档简介
8.3.2 利用二元一次方程组解决较复杂的问题
一、选择题
1.已知∠A、∠B互余,∠A比∠B大30°,设∠A、∠B的度数分别x°,y°.下列方程组中符合题意的是( )
A. B. C. D.
2.小明在某商店购买商品A,B共两次,这两次购买商品A,B的数量和费用如表:
购买商品A的数量(个) 购买商品B的数量(个) 购买总费用(元)
第一次购物 4 3 93
第二次购物 6 6 162
若小丽需要购买2个商品A和3个商品B,则她要花费( )
A.67元 B.68元 C.69元 D.70元
3.如图所示的两台天平保持平衡,已知每块巧克力的质量相等,且每个果冻的质量也相等,则每块巧克力和每个果冻的质量分别为( )
A.10 g,40 g B.15 g,35 g C.20 g,30 g D.30 g,20 g
4.已知有若干片相同的拼图,其形状如图①所示.当4片拼图紧密拼成一列时,总长度为23 cm,如图②所示;当10片拼图紧密拼成一列时,总长度为56 cm,如图③所示,则图①中的拼图长度为( )
A.5.5 cm B.5.6 cm C.5.75 cm D.6.5 cm
5.无人知甲、乙两人年龄,只知道当甲是乙现在的年龄时,乙只有2岁;当乙到甲现在的年龄时,甲是38岁了,则甲、乙现在的年龄各是( )
A.24岁、14岁 B.26岁、14岁 C.26岁、16岁 D.28岁、16岁
二、填空题
6.某车间有60名工人生产太阳镜,1名工人每天可生产镜片200片或镜架50个.应如何分配工人生产镜片和镜架,才能使产品配套?设安排x名工人生产镜片,y名工人生产镜架,则可列方程组为 .
7.一个两位数,两个数位上的数字一个是另一个的2倍.若把此两位数的两个数字对调,所得新数比原数大27,则此两位数是 .
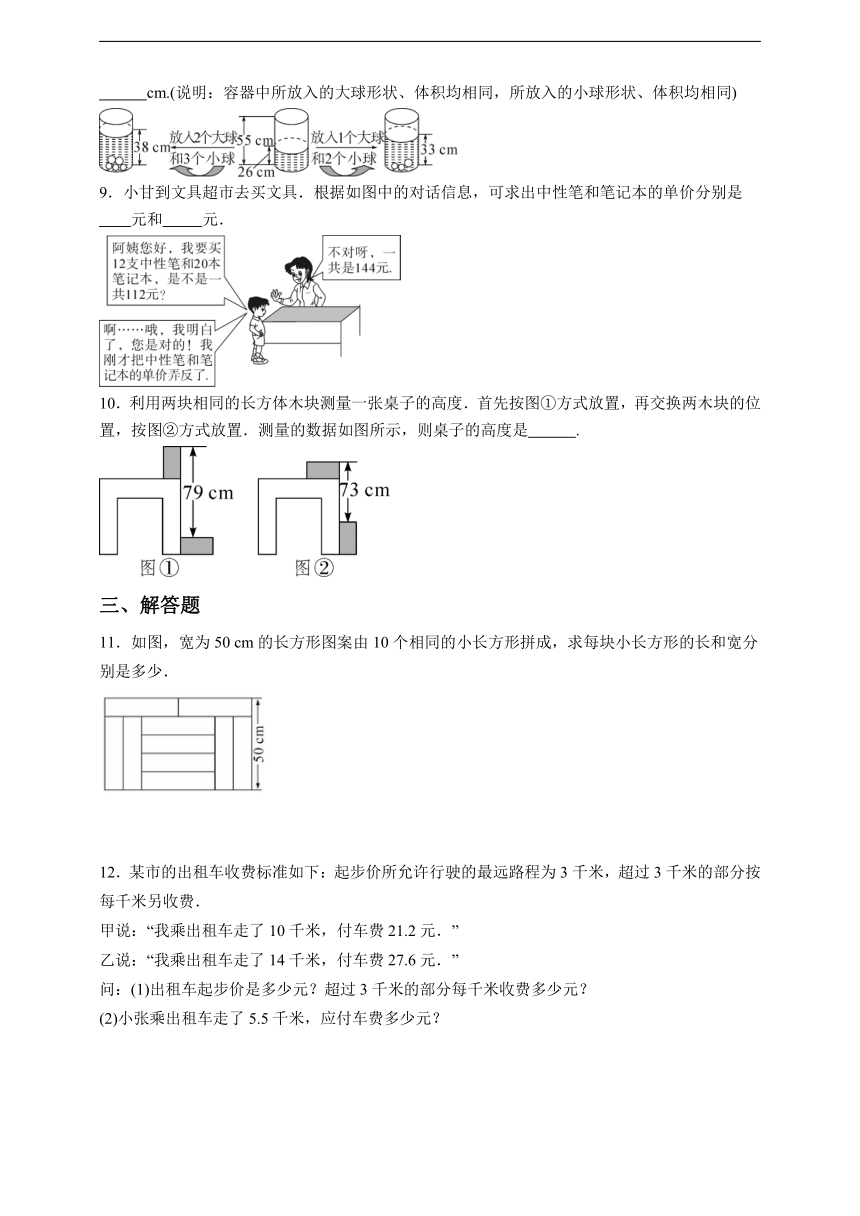
8.根据如图给出的信息:若放入体积相同的大球、体积相同的小球各2个,水面将上升到
cm.(说明:容器中所放入的大球形状、体积均相同,所放入的小球形状、体积均相同)
9.小甘到文具超市去买文具.根据如图中的对话信息,可求出中性笔和笔记本的单价分别是
元和 元.
10.利用两块相同的长方体木块测量一张桌子的高度.首先按图①方式放置,再交换两木块的位置,按图②方式放置.测量的数据如图所示,则桌子的高度是 .
三、解答题
11.如图,宽为50 cm的长方形图案由10个相同的小长方形拼成,求每块小长方形的长和宽分别是多少.
12.某市的出租车收费标准如下:起步价所允许行驶的最远路程为3千米,超过3千米的部分按每千米另收费.
甲说:“我乘出租车走了10千米,付车费21.2元.”
乙说:“我乘出租车走了14千米,付车费27.6元.”
问:(1)出租车起步价是多少元?超过3千米的部分每千米收费多少元?
(2)小张乘出租车走了5.5千米,应付车费多少元?
13.一个长方形养鸡场的长边靠墙,墙长14米,其他三边用篱笆围成,现有长为35米的篱笆,爸爸的设计方案是长比宽多5米;妈妈的设计方案是长比宽多2米.你认为谁的设计合理,为什么?如果按这种设计,养鸡场的面积是多少?
14.某旅行团到森林游乐区参观,如表为两种参观方式与所需的缆车费用.已知旅行团的每个人皆从这两种方式中选择一种,且去程有15人搭乘缆车,回程有10人搭乘缆车.若他们缆车费用的总花费为4100元,则此旅行团共有多少人?
参观方式 缆车费用
去程及回程均搭乘缆车 300元
单程搭乘缆车,单程步行 200元
15.我国古代的优秀数学著作《九章算术》有一道“竹九节”问题,大意是说:现有一根上细下粗共九节的竹子,自上而下从第2节开始,每一节与前一节的容积之差都相等,且最上面三节的容积共9升,最下面三节的容积共45升,求第五节的容积,及每一节与前一节的容积之差.请解答上述问题.
16.学校计划向某花卉供应商家定制一批花卉来装扮校园(花盆全部为同一型号),该商家委托某货运公司负责这批花卉的运输工作.该货运公司有甲、乙两种专门运输花卉的货车,已知1辆甲型货车和3辆乙型货车满载一次可运输1700盆花卉;3辆甲型货车和1辆乙型货车满载一次可运输1900盆花卉.
(1)求1辆甲型货车满载一次可运输多少盆花卉,1辆乙型货车满载一次可运输多少盆花卉;
(2)学校计划定制6500盆花卉,该货运公司将同时派出甲型货车m辆、乙型货车n辆来运输这批花卉,一次性运输完毕,并且每辆货车都满载,请问有哪几种运输方案?
参考答案
一、选择题
1.已知∠A、∠B互余,∠A比∠B大30°,设∠A、∠B的度数分别x°,y°.下列方程组中符合题意的是( D )
A. B. C. D.
2.小明在某商店购买商品A,B共两次,这两次购买商品A,B的数量和费用如表:
购买商品A的数量(个) 购买商品B的数量(个) 购买总费用(元)
第一次购物 4 3 93
第二次购物 6 6 162
若小丽需要购买2个商品A和3个商品B,则她要花费( C )
A.67元 B.68元 C.69元 D.70元
3.如图所示的两台天平保持平衡,已知每块巧克力的质量相等,且每个果冻的质量也相等,则每块巧克力和每个果冻的质量分别为( C )
A.10 g,40 g B.15 g,35 g C.20 g,30 g D.30 g,20 g
4.已知有若干片相同的拼图,其形状如图①所示.当4片拼图紧密拼成一列时,总长度为23 cm,如图②所示;当10片拼图紧密拼成一列时,总长度为56 cm,如图③所示,则图①中的拼图长度为( D )
A.5.5 cm B.5.6 cm C.5.75 cm D.6.5 cm
5.无人知甲、乙两人年龄,只知道当甲是乙现在的年龄时,乙只有2岁;当乙到甲现在的年龄时,甲是38岁了,则甲、乙现在的年龄各是( B )
A.24岁、14岁 B.26岁、14岁 C.26岁、16岁 D.28岁、16岁
二、填空题
6.某车间有60名工人生产太阳镜,1名工人每天可生产镜片200片或镜架50个.应如何分配工人生产镜片和镜架,才能使产品配套?设安排x名工人生产镜片,y名工人生产镜架,则可列方程组为 .
【答案】
7.一个两位数,两个数位上的数字一个是另一个的2倍.若把此两位数的两个数字对调,所得新数比原数大27,则此两位数是 .
【答案】36
8.根据如图给出的信息:若放入体积相同的大球、体积相同的小球各2个,水面将上升到
cm.(说明:容器中所放入的大球形状、体积均相同,所放入的小球形状、体积均相同)
【答案】36
9.小甘到文具超市去买文具.根据如图中的对话信息,可求出中性笔和笔记本的单价分别是
元和 元.
【解析】设中性笔和笔记本的单价分别是x元、y元.根据题意可得解得即中性笔和笔记本的单价分别是2元、6元.
【答案】2 6
10.利用两块相同的长方体木块测量一张桌子的高度.首先按图①方式放置,再交换两木块的位置,按图②方式放置.测量的数据如图所示,则桌子的高度是 .
【解析】设图中长方体木块较长边为x cm,较短边为y cm,桌子的高为a cm,由题意得两式相加得2a=152,解得a=76.故答案为76 cm.
【答案】76cm
三、解答题
11.如图,宽为50 cm的长方形图案由10个相同的小长方形拼成,求每块小长方形的长和宽分别是多少.
解:设每块小长方形的长是x cm,
宽是y cm,
根据题意得解得
答:小长方形的长为40 cm,宽为10 cm.
12.某市的出租车收费标准如下:起步价所允许行驶的最远路程为3千米,超过3千米的部分按每千米另收费.
甲说:“我乘出租车走了10千米,付车费21.2元.”
乙说:“我乘出租车走了14千米,付车费27.6元.”
问:(1)出租车起步价是多少元?超过3千米的部分每千米收费多少元?
解:设出租车起步价是x元,
超过3千米的部分每千米收费y元,
由题意得解得
答:出租车起步价是10元,超过3千米的部分每千米收费1.6元.
(2)小张乘出租车走了5.5千米,应付车费多少元?
解:10+(5.5-3)×1.6=14(元),
即小张乘出租车走了5.5千米,应付车费14元.
13.一个长方形养鸡场的长边靠墙,墙长14米,其他三边用篱笆围成,现有长为35米的篱笆,爸爸的设计方案是长比宽多5米;妈妈的设计方案是长比宽多2米.你认为谁的设计合理,为什么?如果按这种设计,养鸡场的面积是多少?
解:妈妈的设计合理.理由如下:设爸爸的设计方案中养鸡场的宽为x米,长为y米,根据题意得解得∵y=15>14,∴不符合题意.设妈妈的设计方案中养鸡场的宽为a米,长为b米,根据题意得解得∵b=13<14,∴妈妈的设计合理.此时养鸡场的面积为11×13=143(平方米).
14.某旅行团到森林游乐区参观,如表为两种参观方式与所需的缆车费用.已知旅行团的每个人皆从这两种方式中选择一种,且去程有15人搭乘缆车,回程有10人搭乘缆车.若他们缆车费用的总花费为4100元,则此旅行团共有多少人?
参观方式 缆车费用
去程及回程均搭乘缆车 300元
单程搭乘缆车,单程步行 200元
解:设此旅行团有x人单程搭乘缆车,单程步行,有y人去程及回程均搭乘缆车.
根据题意,得解得
则总人数为7+9=16.
答:此旅行团共有16人.
15.我国古代的优秀数学著作《九章算术》有一道“竹九节”问题,大意是说:现有一根上细下粗共九节的竹子,自上而下从第2节开始,每一节与前一节的容积之差都相等,且最上面三节的容积共9升,最下面三节的容积共45升,求第五节的容积,及每一节与前一节的容积之差.请解答上述问题.
解:设第五节的容积为x升,每一节与前一节的容积之差为y升,依题意得
解得
答:第五节的容积为9升,每一节与前一节的容积之差为2升.
16.学校计划向某花卉供应商家定制一批花卉来装扮校园(花盆全部为同一型号),该商家委托某货运公司负责这批花卉的运输工作.该货运公司有甲、乙两种专门运输花卉的货车,已知1辆甲型货车和3辆乙型货车满载一次可运输1700盆花卉;3辆甲型货车和1辆乙型货车满载一次可运输1900盆花卉.
(1)求1辆甲型货车满载一次可运输多少盆花卉,1辆乙型货车满载一次可运输多少盆花卉;
解:设1辆甲型货车满载一次可运输x盆花卉,1辆乙型货车满载一次可运输y盆花卉,
依题意得解得
答:1辆甲型货车满载一次可运输500盆花卉,1辆乙型货车满载一次可运输400盆花卉.
(2)学校计划定制6500盆花卉,该货运公司将同时派出甲型货车m辆、乙型货车n辆来运输这批花卉,一次性运输完毕,并且每辆货车都满载,请问有哪几种运输方案?
解:依题意得500m+400n=6500,∴m=13-n.
又∵m,n均为正整数,
∴或或
∴共有3种运输方案,
方案1:该货运公司派出甲型货车9辆,乙型货车5辆;
方案2:该货运公司派出甲型货车5辆,乙型货车10辆;
方案3:该货运公司派出甲型货车1辆,乙型货车15辆.
一、选择题
1.已知∠A、∠B互余,∠A比∠B大30°,设∠A、∠B的度数分别x°,y°.下列方程组中符合题意的是( )
A. B. C. D.
2.小明在某商店购买商品A,B共两次,这两次购买商品A,B的数量和费用如表:
购买商品A的数量(个) 购买商品B的数量(个) 购买总费用(元)
第一次购物 4 3 93
第二次购物 6 6 162
若小丽需要购买2个商品A和3个商品B,则她要花费( )
A.67元 B.68元 C.69元 D.70元
3.如图所示的两台天平保持平衡,已知每块巧克力的质量相等,且每个果冻的质量也相等,则每块巧克力和每个果冻的质量分别为( )
A.10 g,40 g B.15 g,35 g C.20 g,30 g D.30 g,20 g
4.已知有若干片相同的拼图,其形状如图①所示.当4片拼图紧密拼成一列时,总长度为23 cm,如图②所示;当10片拼图紧密拼成一列时,总长度为56 cm,如图③所示,则图①中的拼图长度为( )
A.5.5 cm B.5.6 cm C.5.75 cm D.6.5 cm
5.无人知甲、乙两人年龄,只知道当甲是乙现在的年龄时,乙只有2岁;当乙到甲现在的年龄时,甲是38岁了,则甲、乙现在的年龄各是( )
A.24岁、14岁 B.26岁、14岁 C.26岁、16岁 D.28岁、16岁
二、填空题
6.某车间有60名工人生产太阳镜,1名工人每天可生产镜片200片或镜架50个.应如何分配工人生产镜片和镜架,才能使产品配套?设安排x名工人生产镜片,y名工人生产镜架,则可列方程组为 .
7.一个两位数,两个数位上的数字一个是另一个的2倍.若把此两位数的两个数字对调,所得新数比原数大27,则此两位数是 .
8.根据如图给出的信息:若放入体积相同的大球、体积相同的小球各2个,水面将上升到
cm.(说明:容器中所放入的大球形状、体积均相同,所放入的小球形状、体积均相同)
9.小甘到文具超市去买文具.根据如图中的对话信息,可求出中性笔和笔记本的单价分别是
元和 元.
10.利用两块相同的长方体木块测量一张桌子的高度.首先按图①方式放置,再交换两木块的位置,按图②方式放置.测量的数据如图所示,则桌子的高度是 .
三、解答题
11.如图,宽为50 cm的长方形图案由10个相同的小长方形拼成,求每块小长方形的长和宽分别是多少.
12.某市的出租车收费标准如下:起步价所允许行驶的最远路程为3千米,超过3千米的部分按每千米另收费.
甲说:“我乘出租车走了10千米,付车费21.2元.”
乙说:“我乘出租车走了14千米,付车费27.6元.”
问:(1)出租车起步价是多少元?超过3千米的部分每千米收费多少元?
(2)小张乘出租车走了5.5千米,应付车费多少元?
13.一个长方形养鸡场的长边靠墙,墙长14米,其他三边用篱笆围成,现有长为35米的篱笆,爸爸的设计方案是长比宽多5米;妈妈的设计方案是长比宽多2米.你认为谁的设计合理,为什么?如果按这种设计,养鸡场的面积是多少?
14.某旅行团到森林游乐区参观,如表为两种参观方式与所需的缆车费用.已知旅行团的每个人皆从这两种方式中选择一种,且去程有15人搭乘缆车,回程有10人搭乘缆车.若他们缆车费用的总花费为4100元,则此旅行团共有多少人?
参观方式 缆车费用
去程及回程均搭乘缆车 300元
单程搭乘缆车,单程步行 200元
15.我国古代的优秀数学著作《九章算术》有一道“竹九节”问题,大意是说:现有一根上细下粗共九节的竹子,自上而下从第2节开始,每一节与前一节的容积之差都相等,且最上面三节的容积共9升,最下面三节的容积共45升,求第五节的容积,及每一节与前一节的容积之差.请解答上述问题.
16.学校计划向某花卉供应商家定制一批花卉来装扮校园(花盆全部为同一型号),该商家委托某货运公司负责这批花卉的运输工作.该货运公司有甲、乙两种专门运输花卉的货车,已知1辆甲型货车和3辆乙型货车满载一次可运输1700盆花卉;3辆甲型货车和1辆乙型货车满载一次可运输1900盆花卉.
(1)求1辆甲型货车满载一次可运输多少盆花卉,1辆乙型货车满载一次可运输多少盆花卉;
(2)学校计划定制6500盆花卉,该货运公司将同时派出甲型货车m辆、乙型货车n辆来运输这批花卉,一次性运输完毕,并且每辆货车都满载,请问有哪几种运输方案?
参考答案
一、选择题
1.已知∠A、∠B互余,∠A比∠B大30°,设∠A、∠B的度数分别x°,y°.下列方程组中符合题意的是( D )
A. B. C. D.
2.小明在某商店购买商品A,B共两次,这两次购买商品A,B的数量和费用如表:
购买商品A的数量(个) 购买商品B的数量(个) 购买总费用(元)
第一次购物 4 3 93
第二次购物 6 6 162
若小丽需要购买2个商品A和3个商品B,则她要花费( C )
A.67元 B.68元 C.69元 D.70元
3.如图所示的两台天平保持平衡,已知每块巧克力的质量相等,且每个果冻的质量也相等,则每块巧克力和每个果冻的质量分别为( C )
A.10 g,40 g B.15 g,35 g C.20 g,30 g D.30 g,20 g
4.已知有若干片相同的拼图,其形状如图①所示.当4片拼图紧密拼成一列时,总长度为23 cm,如图②所示;当10片拼图紧密拼成一列时,总长度为56 cm,如图③所示,则图①中的拼图长度为( D )
A.5.5 cm B.5.6 cm C.5.75 cm D.6.5 cm
5.无人知甲、乙两人年龄,只知道当甲是乙现在的年龄时,乙只有2岁;当乙到甲现在的年龄时,甲是38岁了,则甲、乙现在的年龄各是( B )
A.24岁、14岁 B.26岁、14岁 C.26岁、16岁 D.28岁、16岁
二、填空题
6.某车间有60名工人生产太阳镜,1名工人每天可生产镜片200片或镜架50个.应如何分配工人生产镜片和镜架,才能使产品配套?设安排x名工人生产镜片,y名工人生产镜架,则可列方程组为 .
【答案】
7.一个两位数,两个数位上的数字一个是另一个的2倍.若把此两位数的两个数字对调,所得新数比原数大27,则此两位数是 .
【答案】36
8.根据如图给出的信息:若放入体积相同的大球、体积相同的小球各2个,水面将上升到
cm.(说明:容器中所放入的大球形状、体积均相同,所放入的小球形状、体积均相同)
【答案】36
9.小甘到文具超市去买文具.根据如图中的对话信息,可求出中性笔和笔记本的单价分别是
元和 元.
【解析】设中性笔和笔记本的单价分别是x元、y元.根据题意可得解得即中性笔和笔记本的单价分别是2元、6元.
【答案】2 6
10.利用两块相同的长方体木块测量一张桌子的高度.首先按图①方式放置,再交换两木块的位置,按图②方式放置.测量的数据如图所示,则桌子的高度是 .
【解析】设图中长方体木块较长边为x cm,较短边为y cm,桌子的高为a cm,由题意得两式相加得2a=152,解得a=76.故答案为76 cm.
【答案】76cm
三、解答题
11.如图,宽为50 cm的长方形图案由10个相同的小长方形拼成,求每块小长方形的长和宽分别是多少.
解:设每块小长方形的长是x cm,
宽是y cm,
根据题意得解得
答:小长方形的长为40 cm,宽为10 cm.
12.某市的出租车收费标准如下:起步价所允许行驶的最远路程为3千米,超过3千米的部分按每千米另收费.
甲说:“我乘出租车走了10千米,付车费21.2元.”
乙说:“我乘出租车走了14千米,付车费27.6元.”
问:(1)出租车起步价是多少元?超过3千米的部分每千米收费多少元?
解:设出租车起步价是x元,
超过3千米的部分每千米收费y元,
由题意得解得
答:出租车起步价是10元,超过3千米的部分每千米收费1.6元.
(2)小张乘出租车走了5.5千米,应付车费多少元?
解:10+(5.5-3)×1.6=14(元),
即小张乘出租车走了5.5千米,应付车费14元.
13.一个长方形养鸡场的长边靠墙,墙长14米,其他三边用篱笆围成,现有长为35米的篱笆,爸爸的设计方案是长比宽多5米;妈妈的设计方案是长比宽多2米.你认为谁的设计合理,为什么?如果按这种设计,养鸡场的面积是多少?
解:妈妈的设计合理.理由如下:设爸爸的设计方案中养鸡场的宽为x米,长为y米,根据题意得解得∵y=15>14,∴不符合题意.设妈妈的设计方案中养鸡场的宽为a米,长为b米,根据题意得解得∵b=13<14,∴妈妈的设计合理.此时养鸡场的面积为11×13=143(平方米).
14.某旅行团到森林游乐区参观,如表为两种参观方式与所需的缆车费用.已知旅行团的每个人皆从这两种方式中选择一种,且去程有15人搭乘缆车,回程有10人搭乘缆车.若他们缆车费用的总花费为4100元,则此旅行团共有多少人?
参观方式 缆车费用
去程及回程均搭乘缆车 300元
单程搭乘缆车,单程步行 200元
解:设此旅行团有x人单程搭乘缆车,单程步行,有y人去程及回程均搭乘缆车.
根据题意,得解得
则总人数为7+9=16.
答:此旅行团共有16人.
15.我国古代的优秀数学著作《九章算术》有一道“竹九节”问题,大意是说:现有一根上细下粗共九节的竹子,自上而下从第2节开始,每一节与前一节的容积之差都相等,且最上面三节的容积共9升,最下面三节的容积共45升,求第五节的容积,及每一节与前一节的容积之差.请解答上述问题.
解:设第五节的容积为x升,每一节与前一节的容积之差为y升,依题意得
解得
答:第五节的容积为9升,每一节与前一节的容积之差为2升.
16.学校计划向某花卉供应商家定制一批花卉来装扮校园(花盆全部为同一型号),该商家委托某货运公司负责这批花卉的运输工作.该货运公司有甲、乙两种专门运输花卉的货车,已知1辆甲型货车和3辆乙型货车满载一次可运输1700盆花卉;3辆甲型货车和1辆乙型货车满载一次可运输1900盆花卉.
(1)求1辆甲型货车满载一次可运输多少盆花卉,1辆乙型货车满载一次可运输多少盆花卉;
解:设1辆甲型货车满载一次可运输x盆花卉,1辆乙型货车满载一次可运输y盆花卉,
依题意得解得
答:1辆甲型货车满载一次可运输500盆花卉,1辆乙型货车满载一次可运输400盆花卉.
(2)学校计划定制6500盆花卉,该货运公司将同时派出甲型货车m辆、乙型货车n辆来运输这批花卉,一次性运输完毕,并且每辆货车都满载,请问有哪几种运输方案?
解:依题意得500m+400n=6500,∴m=13-n.
又∵m,n均为正整数,
∴或或
∴共有3种运输方案,
方案1:该货运公司派出甲型货车9辆,乙型货车5辆;
方案2:该货运公司派出甲型货车5辆,乙型货车10辆;
方案3:该货运公司派出甲型货车1辆,乙型货车15辆.
