四年级下册数学冀教版 第九单元 探索多边形中隐含的规律(课件)(共18张PPT)
文档属性
| 名称 | 四年级下册数学冀教版 第九单元 探索多边形中隐含的规律(课件)(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 731.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-04 00:00:00 | ||
图片预览




文档简介
(共18张PPT)
冀教版四年级下册数学第九单元 探索乐园
探索多边形中隐含的规律
像这样,在同一平面内,由三条或三条以上的线段首尾顺次连接所组成的封闭图形叫做多边形。
多边形的定义
……
五边形
六边形
七边形
三角形
四边形
认真观察四边形、五边形,说说它们是怎样分割成三角形的?
.
.
观 察
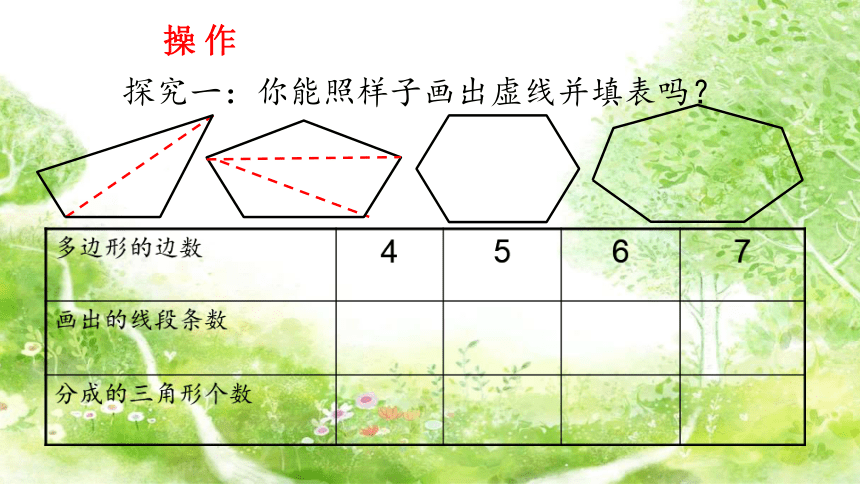
探究一:你能照样子画出虚线并填表吗?
操 作
3
4
4
5
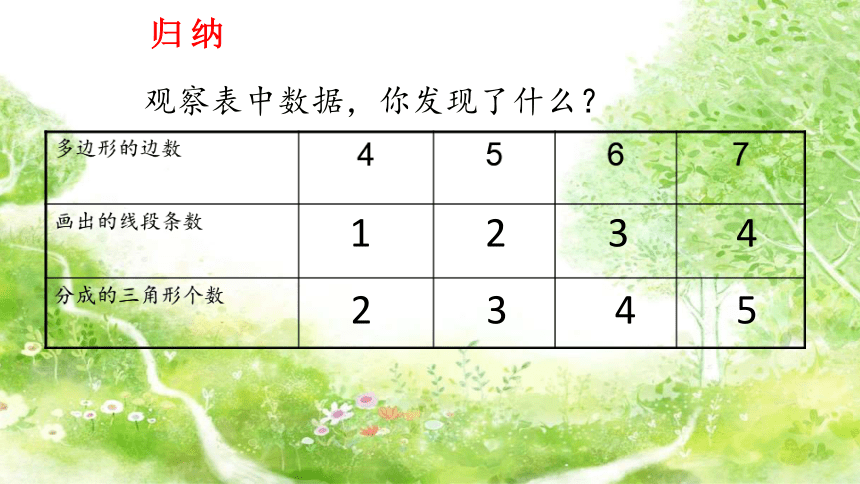
观察表中数据,你发现了什么?
1
2
2
3
归 纳
根据发现的规律快速填表
5
7
47
6
8
48
n边形从一个顶点出发可以画出_____条线段,
分割成_____个三角形。
8
10
50
……
回顾探索,总结方法
初探:四边形的内角和
结论:四边形的内角和为2×1800=3600
1
2
3
4
5
6
四边形的内角和
观察表中的数据,说说你发现什么?
分成的三角形个数
多边形的内角和
多边形的内角和= ×180°
三角形的个数
多边形的内角和= ×180°
(边数-2)
探究二:多边形的内角和
5
3
3×180°
=540°
6
4
4×180°
=720°
7
5
5×180°
=900°
4
2
2×180°
=360°
边数
观察表中的数据,说说你有什么发现?
5
3
3×180°
=540°
6
4
4×180°
=720°
7
5
5×180°
=900°
4
2
2×180°
=360°
n边形的内角和是______________________
分成的三角形个数
多边形的内角和
边数
探究二:多边形的内角和
当n=12时,多边形的内角和是多少度?
180°×(12-2)
=180°×10
=1800°
答:当n=12时,多边形的内角和是1800°
根据发现的规律解决问题
布局精巧玄妙,从高空俯视,全村呈八卦形,房屋、街巷的分布走向恰好与历史上写的诸葛亮九宫八卦阵暗合。
应用规律
浙江金华兰溪诸葛八卦村
你能算出八卦图的内角和吗?
小明在数学日记里写道:我有个愿望,想在2160年设计一个多边形,让它的内角和是2160°,小明的愿望能实现吗? 说说你的理由。
应用规律
回顾探索规律的过程,谈谈你的收获。
课后作业:数学课本99页,练一练
冀教版四年级下册数学第九单元 探索乐园
探索多边形中隐含的规律
像这样,在同一平面内,由三条或三条以上的线段首尾顺次连接所组成的封闭图形叫做多边形。
多边形的定义
……
五边形
六边形
七边形
三角形
四边形
认真观察四边形、五边形,说说它们是怎样分割成三角形的?
.
.
观 察
探究一:你能照样子画出虚线并填表吗?
操 作
3
4
4
5
观察表中数据,你发现了什么?
1
2
2
3
归 纳
根据发现的规律快速填表
5
7
47
6
8
48
n边形从一个顶点出发可以画出_____条线段,
分割成_____个三角形。
8
10
50
……
回顾探索,总结方法
初探:四边形的内角和
结论:四边形的内角和为2×1800=3600
1
2
3
4
5
6
四边形的内角和
观察表中的数据,说说你发现什么?
分成的三角形个数
多边形的内角和
多边形的内角和= ×180°
三角形的个数
多边形的内角和= ×180°
(边数-2)
探究二:多边形的内角和
5
3
3×180°
=540°
6
4
4×180°
=720°
7
5
5×180°
=900°
4
2
2×180°
=360°
边数
观察表中的数据,说说你有什么发现?
5
3
3×180°
=540°
6
4
4×180°
=720°
7
5
5×180°
=900°
4
2
2×180°
=360°
n边形的内角和是______________________
分成的三角形个数
多边形的内角和
边数
探究二:多边形的内角和
当n=12时,多边形的内角和是多少度?
180°×(12-2)
=180°×10
=1800°
答:当n=12时,多边形的内角和是1800°
根据发现的规律解决问题
布局精巧玄妙,从高空俯视,全村呈八卦形,房屋、街巷的分布走向恰好与历史上写的诸葛亮九宫八卦阵暗合。
应用规律
浙江金华兰溪诸葛八卦村
你能算出八卦图的内角和吗?
小明在数学日记里写道:我有个愿望,想在2160年设计一个多边形,让它的内角和是2160°,小明的愿望能实现吗? 说说你的理由。
应用规律
回顾探索规律的过程,谈谈你的收获。
课后作业:数学课本99页,练一练
