六年级下册数学苏教版第二章圆柱和圆锥复习课件(共24张PPT)
文档属性
| 名称 | 六年级下册数学苏教版第二章圆柱和圆锥复习课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 500.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-05 00:00:00 | ||
图片预览







文档简介
(共24张PPT)
第二章圆柱和圆锥复习
苏教版小学数学六年级下册
学习目标
1、通过复习,使学生比较系统地掌握本单元所学的立体图形知识,认识圆柱、圆锥的特征和它们的体积之间的联系与区别,掌握圆柱表面积、体积,圆锥体积的计算公式,能正确计算。
2、学生的空间观念,培养学生有条理地对所学知识进行整理归纳的能力。
学习重点:
圆柱表面积及圆柱、圆锥、体积的计算
学习难点:
圆锥的特征和它们的体积之间的联系与区别
一、基础训练:
1、一个圆柱的底面半径是3厘米,高是2厘米,
这个圆柱的底面周长是( )厘米,底面积是( )平方厘米,侧面积是( )平方厘米,
表面积是( )平方厘米,体积是( )立方厘米,和它等底等高的圆锥的体积是( )立方厘米.
2、一个圆柱体和一个圆锥体半径之比是1∶2,
高之比是2∶5,它们体积之比是( )。
3、一个圆柱的侧面展开得到一个长方形,长方形的
长是9.42厘米,宽是3厘米,这个圆柱体的侧面积
是( )平方厘米,表面积是( )平方厘米,
体积是( )立方厘米,
将它削成一个最大的圆锥体,应削去( )立方厘米.
4、一个圆柱体和一个圆锥体的体积相等,它们底面积的比是3:5,圆柱的高8厘米,圆锥的高是( )厘米.
5、一个圆柱和圆锥等底等高,圆柱体积比圆锥体积
多30立方厘米.圆柱的体积是( )立方厘米,
圆锥的体积是( )立方厘米.
6、将棱长为6分米的正方体木块,削成一个最大的
圆锥体,这个圆锥的体积是( )立方分米,
一共削去( )立方分米的木料.
7、将一张长12.56厘米,宽9.42厘米的长方形纸卷成
一个圆柱体,圆柱体的体积是( )立方厘米
或( )立方厘米.
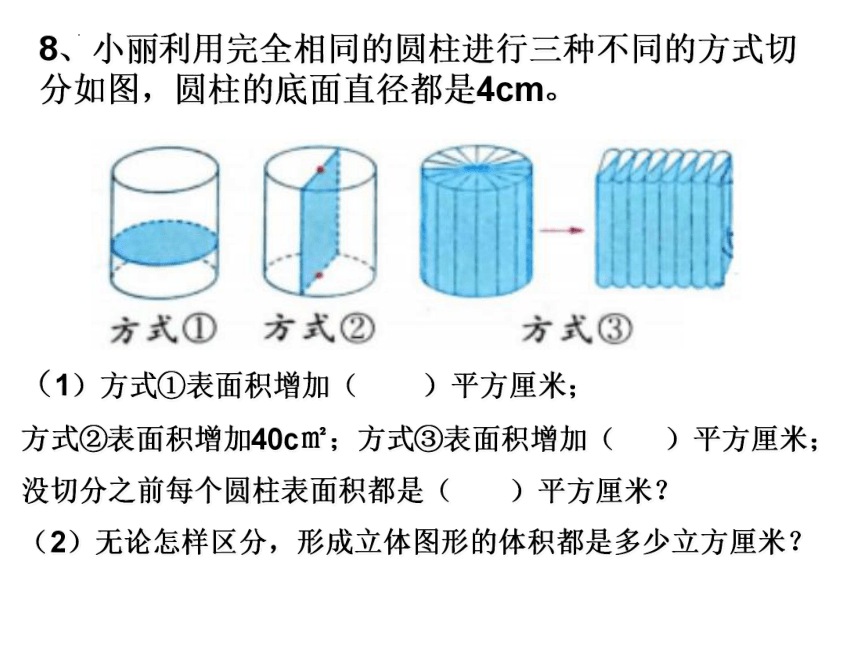
8、小丽利用完全相同的圆柱进行三种不同的方式切分如图,圆柱的底面直径都是4cm。
(1)方式①表面积增加( )平方厘米;
方式②表面积增加40c㎡;方式③表面积增加( )平方厘米;没切分之前每个圆柱表面积都是( )平方厘米?
(2)无论怎样区分,形成立体图形的体积都是多少立方厘米?
9、如图,有两个缺口的圆柱形水桶,
最多能盛水多少升?
10、圆柱型玻璃杯中盛有水,水面高5厘米,底面直径
为8厘米,在杯中垂直放入底面直径4厘米,高6厘米的
圆柱体后,水面没有淹没圆柱体,这时水面高多少
厘米?
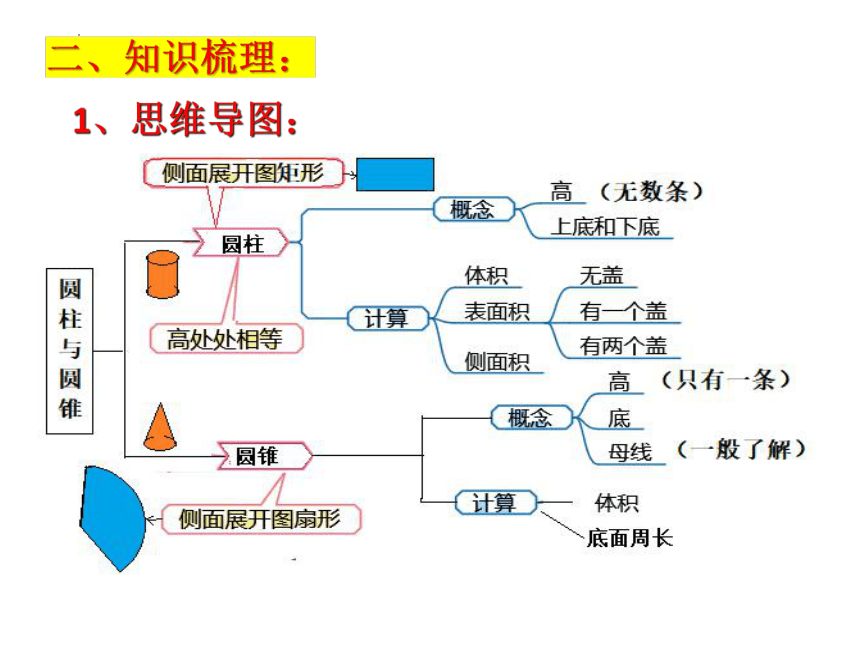
二、知识梳理:
1、思维导图:
2、知识要点:
(1)圆柱:以矩形的一边所在直线为旋转轴,
其余三边旋转形成的几何体叫做圆柱。
底面是有两个完全相同的圆组成,侧面是一个曲面,
侧面展开是一个长方形。
长方形的长=底面周长,宽=高 有无数条高;
圆柱底面积=πr2, 侧面积=2πrh,
表面积=2πr2+2πrh.(有底有盖)。体积=πr2h。
(2)圆锥:以直角三角形的一边所在直线为旋转轴,
旋转形成的几何体叫做圆锥。
圆锥只有一个底面,侧面是一个曲面,
展开是一个扇形,只有一条高。
圆柱底面积=πr2,体积= πr2h。
(3)与圆柱等底等高的圆锥体积是圆柱体积的 .
体积和高相等的圆锥与圆柱(等低等高),
圆锥的底面积是圆柱的3倍。
体积和底面积相等的圆锥与圆柱(等低等高),
圆锥的高是圆柱的3倍。
三、问题研讨:
例1、某小区在平坦的空地上修建一个底面半径
为10米的圆柱形游泳池池深1.2米
(1)游泳池占地面积多少平方米?
(2)在池底和侧面都铺上瓷砖,铺瓷砖的面积
是多少平方米?
(3)修建游泳池需挖多少立方米的泥土
例2、在一个圆柱形的水桶里,放一段半径是5厘米的圆钢,如果把它完全放入水中,桶里的水就上升9厘米,如果把水中的圆钢露出水面8厘米,那么,这时桶里的水就下降4厘米.求圆钢的体积
例3、有A、B两个圆柱形容器,最初在容器A里装有2升水,容器B是空的。现在往两个容器中以每分钟0.4升的流量注入水,4分钟后,两个容器的水面高度相等。设B的底面半径为5厘米,那么A的底面直径是多少厘米?
例4、
如图1,计算几何体的表面积和体积。(单位:厘米)
如图2,从圆柱上挖去一个圆锥,求剩下的几何体
的体积。(单位:厘米)
例5、如图是一个酸奶瓶,它的瓶身呈圆柱形(不包括瓶颈),底面半径6厘米,当瓶子正放时,瓶内酸奶高为10厘米,瓶子倒放时,空余部分高为2厘米,请你算一算,这个酸奶瓶子的容积是立方厘米。
四、规律总结:
1、常见的圆柱解决问题:
①压路机压过路面面积、烟囱、教学楼里的
支撑柱、通风管、出水管(求侧面积);
②压路机压过路面长度(求底面周长);
③水桶铁皮(求侧面积和一个底面积);
④鱼缸、厨师帽(求侧面积和一个底面积);
⑤圆形空心钢管的体积=(πR2﹣πr2)×h
2、题型总结:
①高不变,半径扩大(缩小)n倍,直径、底面周长、
侧面积扩大(缩小)n倍,底面积、体积扩大(缩小)n2倍。
②半径不变高扩大(缩小)n倍,侧面积、体积扩大(缩小)n倍。
③削成最大体积的问题:
正方体里削出最大的圆柱、圆锥:
圆柱、圆锥的高和底面直径等于正方体棱长。
长方体里削出最大的圆柱、圆锥:
圆柱、圆锥底面直径等于宽(宽﹥高),
圆柱、圆锥高等于长方体高。
④浸物体积问题(排水法测不规则物体的体积):
水面上升部分的体积就是浸入水中物品的体积,
等于盛水容器的底面积乘上升的高度。
也就是变化的水的体积。
主要类型:①盛满水,浸物溢水;②浸物水面上升;
③取物水面下降。
⑤等体积转换问题:
圆锥体沙堆铺路;长方体钢材熔铸成圆柱或圆锥;
橡皮泥改变形状;圆柱中的溶液倒入圆锥……
都是体积不变的问题。
(一)选择题
1、一个圆锥的体积是12立方厘米,底面积
是4平方厘米,高是( )厘米。
① 3 ② 6 ③ 9 ④ 12
2、一个圆锥的体积是n立方厘米,和它等底等高
的圆柱体的体积是( )立方厘米。
① n ② 2n ③ 3n ④ 3n
3、把一段圆钢切削成一个最大的圆锥体,切削掉的部分部分重8千克,这段圆钢重( )千克。
①24 ②16 ③12 ④8
4、一个底面直径是27厘米,高9厘米的圆锥体木块,分成形状大小完全相同的两个木块后,表面积比原来增加( )平方厘米。
①81 ②243 ③121.5 ④125.6
五、强化训练:
(二)判断题:
1、圆锥体积是圆柱体积的 ( )
2、一个圆锥高不变,底面积扩大到原来的6倍,
这个圆锥的体积也扩大到原来的6倍。 ( )
3、底面半径是6厘米的圆锥体的体积等于底面半径
是2厘米的等高圆柱的体积。 ( )
4、如果两个圆柱体的侧面积相等,那么它们的
底面周长也一定相等。 ( )
5、圆锥的体积是8.1立方分米,高是0.3分米,
底面积是81平方分米。 ( )
3、一个圆柱和一个圆锥等底等高,圆锥的体积比圆柱的体积少0.8立方分米,那么圆锥的体积是( )立方分米,圆柱的体积是( )立方分米.
4、一个圆柱和圆锥等底等高,它们的体积一共60立方
厘米,那么,圆柱的体积是( )立方厘米,
圆锥的体积是( )立方厘米.
5、将一根长5米的圆柱形木料锯成4段,表面积
增加60平方分米,这根木料的体积是( )
立方分米.
(三)解答题:
1、计算下面图形的体积。(单位:厘米)
2、如图,有一个沙漏,上下两部分都是半径12厘米的,高10厘米的圆锥,现在上半部分沙漏已经
装满沙,如果每分钟流出20立方厘米沙,那沙漏里的沙全部流到下半部分需要多少分钟?
3、一个圆柱形麦囤,底面直径为2米,高2米,装满小麦后,又在囤上最大限度地堆成一个高0.6米 的圆锥.每立方米小麦重750千克,小麦的出粉率约是70%,这囤小麦共可碾粉多少千克?(得数保留一位小数)
4、一台压路机前轮的直径是1.5米,宽是2米。
(1)这台压路机前轮高度5周,可以压路多少平方米?
(2)如果这台压路机前轮每分钟转动20周,
那么1小时大约前进多少千米?
(得数保留整数)
第二章圆柱和圆锥复习
苏教版小学数学六年级下册
学习目标
1、通过复习,使学生比较系统地掌握本单元所学的立体图形知识,认识圆柱、圆锥的特征和它们的体积之间的联系与区别,掌握圆柱表面积、体积,圆锥体积的计算公式,能正确计算。
2、学生的空间观念,培养学生有条理地对所学知识进行整理归纳的能力。
学习重点:
圆柱表面积及圆柱、圆锥、体积的计算
学习难点:
圆锥的特征和它们的体积之间的联系与区别
一、基础训练:
1、一个圆柱的底面半径是3厘米,高是2厘米,
这个圆柱的底面周长是( )厘米,底面积是( )平方厘米,侧面积是( )平方厘米,
表面积是( )平方厘米,体积是( )立方厘米,和它等底等高的圆锥的体积是( )立方厘米.
2、一个圆柱体和一个圆锥体半径之比是1∶2,
高之比是2∶5,它们体积之比是( )。
3、一个圆柱的侧面展开得到一个长方形,长方形的
长是9.42厘米,宽是3厘米,这个圆柱体的侧面积
是( )平方厘米,表面积是( )平方厘米,
体积是( )立方厘米,
将它削成一个最大的圆锥体,应削去( )立方厘米.
4、一个圆柱体和一个圆锥体的体积相等,它们底面积的比是3:5,圆柱的高8厘米,圆锥的高是( )厘米.
5、一个圆柱和圆锥等底等高,圆柱体积比圆锥体积
多30立方厘米.圆柱的体积是( )立方厘米,
圆锥的体积是( )立方厘米.
6、将棱长为6分米的正方体木块,削成一个最大的
圆锥体,这个圆锥的体积是( )立方分米,
一共削去( )立方分米的木料.
7、将一张长12.56厘米,宽9.42厘米的长方形纸卷成
一个圆柱体,圆柱体的体积是( )立方厘米
或( )立方厘米.
8、小丽利用完全相同的圆柱进行三种不同的方式切分如图,圆柱的底面直径都是4cm。
(1)方式①表面积增加( )平方厘米;
方式②表面积增加40c㎡;方式③表面积增加( )平方厘米;没切分之前每个圆柱表面积都是( )平方厘米?
(2)无论怎样区分,形成立体图形的体积都是多少立方厘米?
9、如图,有两个缺口的圆柱形水桶,
最多能盛水多少升?
10、圆柱型玻璃杯中盛有水,水面高5厘米,底面直径
为8厘米,在杯中垂直放入底面直径4厘米,高6厘米的
圆柱体后,水面没有淹没圆柱体,这时水面高多少
厘米?
二、知识梳理:
1、思维导图:
2、知识要点:
(1)圆柱:以矩形的一边所在直线为旋转轴,
其余三边旋转形成的几何体叫做圆柱。
底面是有两个完全相同的圆组成,侧面是一个曲面,
侧面展开是一个长方形。
长方形的长=底面周长,宽=高 有无数条高;
圆柱底面积=πr2, 侧面积=2πrh,
表面积=2πr2+2πrh.(有底有盖)。体积=πr2h。
(2)圆锥:以直角三角形的一边所在直线为旋转轴,
旋转形成的几何体叫做圆锥。
圆锥只有一个底面,侧面是一个曲面,
展开是一个扇形,只有一条高。
圆柱底面积=πr2,体积= πr2h。
(3)与圆柱等底等高的圆锥体积是圆柱体积的 .
体积和高相等的圆锥与圆柱(等低等高),
圆锥的底面积是圆柱的3倍。
体积和底面积相等的圆锥与圆柱(等低等高),
圆锥的高是圆柱的3倍。
三、问题研讨:
例1、某小区在平坦的空地上修建一个底面半径
为10米的圆柱形游泳池池深1.2米
(1)游泳池占地面积多少平方米?
(2)在池底和侧面都铺上瓷砖,铺瓷砖的面积
是多少平方米?
(3)修建游泳池需挖多少立方米的泥土
例2、在一个圆柱形的水桶里,放一段半径是5厘米的圆钢,如果把它完全放入水中,桶里的水就上升9厘米,如果把水中的圆钢露出水面8厘米,那么,这时桶里的水就下降4厘米.求圆钢的体积
例3、有A、B两个圆柱形容器,最初在容器A里装有2升水,容器B是空的。现在往两个容器中以每分钟0.4升的流量注入水,4分钟后,两个容器的水面高度相等。设B的底面半径为5厘米,那么A的底面直径是多少厘米?
例4、
如图1,计算几何体的表面积和体积。(单位:厘米)
如图2,从圆柱上挖去一个圆锥,求剩下的几何体
的体积。(单位:厘米)
例5、如图是一个酸奶瓶,它的瓶身呈圆柱形(不包括瓶颈),底面半径6厘米,当瓶子正放时,瓶内酸奶高为10厘米,瓶子倒放时,空余部分高为2厘米,请你算一算,这个酸奶瓶子的容积是立方厘米。
四、规律总结:
1、常见的圆柱解决问题:
①压路机压过路面面积、烟囱、教学楼里的
支撑柱、通风管、出水管(求侧面积);
②压路机压过路面长度(求底面周长);
③水桶铁皮(求侧面积和一个底面积);
④鱼缸、厨师帽(求侧面积和一个底面积);
⑤圆形空心钢管的体积=(πR2﹣πr2)×h
2、题型总结:
①高不变,半径扩大(缩小)n倍,直径、底面周长、
侧面积扩大(缩小)n倍,底面积、体积扩大(缩小)n2倍。
②半径不变高扩大(缩小)n倍,侧面积、体积扩大(缩小)n倍。
③削成最大体积的问题:
正方体里削出最大的圆柱、圆锥:
圆柱、圆锥的高和底面直径等于正方体棱长。
长方体里削出最大的圆柱、圆锥:
圆柱、圆锥底面直径等于宽(宽﹥高),
圆柱、圆锥高等于长方体高。
④浸物体积问题(排水法测不规则物体的体积):
水面上升部分的体积就是浸入水中物品的体积,
等于盛水容器的底面积乘上升的高度。
也就是变化的水的体积。
主要类型:①盛满水,浸物溢水;②浸物水面上升;
③取物水面下降。
⑤等体积转换问题:
圆锥体沙堆铺路;长方体钢材熔铸成圆柱或圆锥;
橡皮泥改变形状;圆柱中的溶液倒入圆锥……
都是体积不变的问题。
(一)选择题
1、一个圆锥的体积是12立方厘米,底面积
是4平方厘米,高是( )厘米。
① 3 ② 6 ③ 9 ④ 12
2、一个圆锥的体积是n立方厘米,和它等底等高
的圆柱体的体积是( )立方厘米。
① n ② 2n ③ 3n ④ 3n
3、把一段圆钢切削成一个最大的圆锥体,切削掉的部分部分重8千克,这段圆钢重( )千克。
①24 ②16 ③12 ④8
4、一个底面直径是27厘米,高9厘米的圆锥体木块,分成形状大小完全相同的两个木块后,表面积比原来增加( )平方厘米。
①81 ②243 ③121.5 ④125.6
五、强化训练:
(二)判断题:
1、圆锥体积是圆柱体积的 ( )
2、一个圆锥高不变,底面积扩大到原来的6倍,
这个圆锥的体积也扩大到原来的6倍。 ( )
3、底面半径是6厘米的圆锥体的体积等于底面半径
是2厘米的等高圆柱的体积。 ( )
4、如果两个圆柱体的侧面积相等,那么它们的
底面周长也一定相等。 ( )
5、圆锥的体积是8.1立方分米,高是0.3分米,
底面积是81平方分米。 ( )
3、一个圆柱和一个圆锥等底等高,圆锥的体积比圆柱的体积少0.8立方分米,那么圆锥的体积是( )立方分米,圆柱的体积是( )立方分米.
4、一个圆柱和圆锥等底等高,它们的体积一共60立方
厘米,那么,圆柱的体积是( )立方厘米,
圆锥的体积是( )立方厘米.
5、将一根长5米的圆柱形木料锯成4段,表面积
增加60平方分米,这根木料的体积是( )
立方分米.
(三)解答题:
1、计算下面图形的体积。(单位:厘米)
2、如图,有一个沙漏,上下两部分都是半径12厘米的,高10厘米的圆锥,现在上半部分沙漏已经
装满沙,如果每分钟流出20立方厘米沙,那沙漏里的沙全部流到下半部分需要多少分钟?
3、一个圆柱形麦囤,底面直径为2米,高2米,装满小麦后,又在囤上最大限度地堆成一个高0.6米 的圆锥.每立方米小麦重750千克,小麦的出粉率约是70%,这囤小麦共可碾粉多少千克?(得数保留一位小数)
4、一台压路机前轮的直径是1.5米,宽是2米。
(1)这台压路机前轮高度5周,可以压路多少平方米?
(2)如果这台压路机前轮每分钟转动20周,
那么1小时大约前进多少千米?
(得数保留整数)
