六年级下册数学冀教版3.1认识成正比例的量(课件)(共24张PPT)
文档属性
| 名称 | 六年级下册数学冀教版3.1认识成正比例的量(课件)(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-05 15:10:31 | ||
图片预览








文档简介
(共24张PPT)
冀教版六年级下册第三单元第1课时
认识成正比例的量
下面是一辆汽车8:00出发时和行驶1小时后里程表上显示的千米数。
里程表记录了汽车从开始行驶到停止行驶所走过的路程。
千米数增加了,增加的千米数是1小时行驶的路程。
说一说:下面的两个里程表表述的是什么意思?
第一个里程表显示的是开始行驶前的千米数。开始前千米数是8724千米。
第二个里程表显示的是行驶1小时后的千米数。一小时后千米数是8814千米。
(1)汽车1小时行驶了多少千米?
8814-8724=90(千米)
答:汽车1小时行驶了90千米。
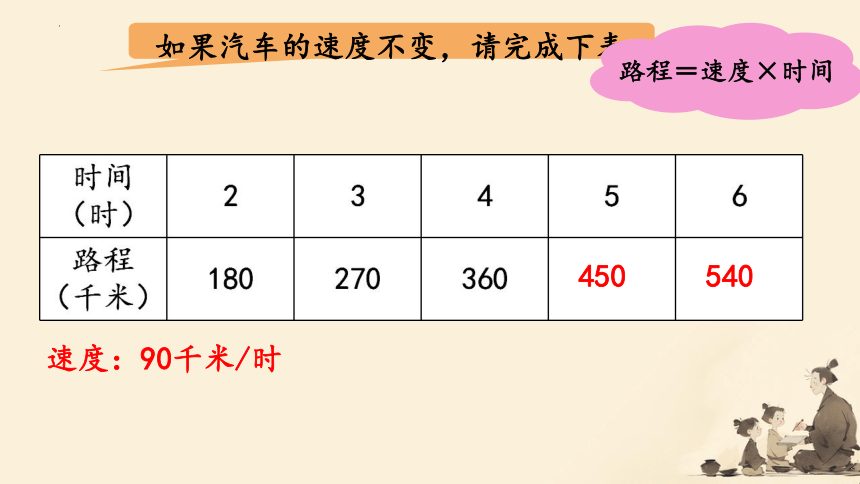
如果汽车的速度不变,请完成下表。
450
540
路程=速度×时间
速度:90千米/时
写出相对应的路程和时间的比并求比值,你发现了什么?
都是用 ,而且比值(速度)都相等。
路程和时间的比值相等,可以说比值一定。
路程和时间的比值相等,可以说比值一定。
在速度一定的情况下,路程和时间有什么关系?
时间越长,行驶的路程越远。
路程越远,需要的时间越长。
观察表格,探究路程和时间的变化规律
(1)找出相关联的量。
从左往右看:
时间扩大到原来的几倍,路程也扩大到原来的几倍。
从右往左看:
时间缩小到原来的几分之几,路程也缩小到原来的几分之几。
路程和时间是两种相关联的量,路程随着时间的变化而变化。
一种量变化,另一种量也随着变化,说明这两种量之间存在着关系,这两种量叫做相关联的量。
相关联的量:
观察表格,探究路程和时间的变化规律。
(2)发现路程和时间的变化规律。
数据无论怎样变化,路程和时间的比值都不变,即速度不变。
路程和时间是两种相关联的量,路程随着时间的变化而变化,而且路程和时间的比值一定(速度一定)。我们就说路程和时间这两种量成正比例。
总结归纳
自动笔的单价为1.6元,请完成下表。
总价=单价×数量
8
9.6
11.2
12.8
从下表中你发现了什么规律?
买自动笔的数量越多,花的钱数就越多……
单价一定,也就是花的钱数和买自动笔数量的比值一定。
花的钱数和买自动笔的数量这两种量成正比例吗?为什么?
花的钱数和买自动笔的数量是两种相关联的量。单价一定,总价随着买自动笔数量的变化而变化。
总价随着数量的变化而变化,数量扩大,总价也扩大;数量缩小,总价也缩小。但是单价是不变的,即总价和数量的比值是一定的,因此,花的钱数和买自动笔的数量两种量成正比例。
像上面这样,两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量叫做成正比例的量。它们的关系叫做正比例关系。
如何判断两种量是否成正比例?
1. 判断两种量是不是两种相关联的量,一种量是否随着另一种量的变化而变化。(一起扩大或者一起缩小)
2.判断这两种量中相对应的两个数的比值是否一定,比值一定,则成正比例,比值不一定,则不成正比例。
1.判断下面各题中的两种量是否成正比例,并说明理由。
(1)飞机飞行的速度不变,飞行的路程和时间。
成正比例,因为 ,所以飞行的路程和时间成正比例。
(2)每千克苹果的价钱一定,付出的钱数和购买苹果的数量。
总价=单价×数量
成正比例。因为
所以付出的钱数和购买苹果的数量成正比例。
1.判断下面各题中的两种量是否成正比例,并说明理由。
(3)每月收入一定,每月支出的钱数和剩下的钱数。
不成正比例,虽然支出的钱数和剩余的钱数也是两种相关联的量,但是这两种量仅仅是一种和差关系,不存在比值一定一说。
3.填空题
(1)成正比例的两种量的变化有一定的规律,他们的( )总是不变。
(2)因为总价÷数量=( )(一定),所以总价和数量成( )比例。
(3)已知5x=3y(x和y均不为0),则x和y成( )比例。
比值
单价
正
正
3.填空题
(4)长方形的长一定,( )和( )成正比例。
(5)一种货物,运走的质量和剩下的质量( )正比例。(填“成”或“不成”)
宽
不成
面积
4.一个化肥厂的生产情况如下表,根据表中数据回答问题。
(1)表中有哪两种相关联的量?
时间和生产量是两种相关联的量。
时间越大,生产量也越大。
4.一个化肥厂的生产情况如下表,根据表中数据回答问题。
(2)表中相关联的两种量成正比例吗?为什么?
时间和生产量成正比例,因为
在判断两种量是否成正比例时,先判断两种量是不是两种相关联的量;再判断这两种量中相对应的两个数的比值是否一定,比值一定,则成正比例,比值不一定,则不成正比例。
冀教版六年级下册第三单元第1课时
认识成正比例的量
下面是一辆汽车8:00出发时和行驶1小时后里程表上显示的千米数。
里程表记录了汽车从开始行驶到停止行驶所走过的路程。
千米数增加了,增加的千米数是1小时行驶的路程。
说一说:下面的两个里程表表述的是什么意思?
第一个里程表显示的是开始行驶前的千米数。开始前千米数是8724千米。
第二个里程表显示的是行驶1小时后的千米数。一小时后千米数是8814千米。
(1)汽车1小时行驶了多少千米?
8814-8724=90(千米)
答:汽车1小时行驶了90千米。
如果汽车的速度不变,请完成下表。
450
540
路程=速度×时间
速度:90千米/时
写出相对应的路程和时间的比并求比值,你发现了什么?
都是用 ,而且比值(速度)都相等。
路程和时间的比值相等,可以说比值一定。
路程和时间的比值相等,可以说比值一定。
在速度一定的情况下,路程和时间有什么关系?
时间越长,行驶的路程越远。
路程越远,需要的时间越长。
观察表格,探究路程和时间的变化规律
(1)找出相关联的量。
从左往右看:
时间扩大到原来的几倍,路程也扩大到原来的几倍。
从右往左看:
时间缩小到原来的几分之几,路程也缩小到原来的几分之几。
路程和时间是两种相关联的量,路程随着时间的变化而变化。
一种量变化,另一种量也随着变化,说明这两种量之间存在着关系,这两种量叫做相关联的量。
相关联的量:
观察表格,探究路程和时间的变化规律。
(2)发现路程和时间的变化规律。
数据无论怎样变化,路程和时间的比值都不变,即速度不变。
路程和时间是两种相关联的量,路程随着时间的变化而变化,而且路程和时间的比值一定(速度一定)。我们就说路程和时间这两种量成正比例。
总结归纳
自动笔的单价为1.6元,请完成下表。
总价=单价×数量
8
9.6
11.2
12.8
从下表中你发现了什么规律?
买自动笔的数量越多,花的钱数就越多……
单价一定,也就是花的钱数和买自动笔数量的比值一定。
花的钱数和买自动笔的数量这两种量成正比例吗?为什么?
花的钱数和买自动笔的数量是两种相关联的量。单价一定,总价随着买自动笔数量的变化而变化。
总价随着数量的变化而变化,数量扩大,总价也扩大;数量缩小,总价也缩小。但是单价是不变的,即总价和数量的比值是一定的,因此,花的钱数和买自动笔的数量两种量成正比例。
像上面这样,两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量叫做成正比例的量。它们的关系叫做正比例关系。
如何判断两种量是否成正比例?
1. 判断两种量是不是两种相关联的量,一种量是否随着另一种量的变化而变化。(一起扩大或者一起缩小)
2.判断这两种量中相对应的两个数的比值是否一定,比值一定,则成正比例,比值不一定,则不成正比例。
1.判断下面各题中的两种量是否成正比例,并说明理由。
(1)飞机飞行的速度不变,飞行的路程和时间。
成正比例,因为 ,所以飞行的路程和时间成正比例。
(2)每千克苹果的价钱一定,付出的钱数和购买苹果的数量。
总价=单价×数量
成正比例。因为
所以付出的钱数和购买苹果的数量成正比例。
1.判断下面各题中的两种量是否成正比例,并说明理由。
(3)每月收入一定,每月支出的钱数和剩下的钱数。
不成正比例,虽然支出的钱数和剩余的钱数也是两种相关联的量,但是这两种量仅仅是一种和差关系,不存在比值一定一说。
3.填空题
(1)成正比例的两种量的变化有一定的规律,他们的( )总是不变。
(2)因为总价÷数量=( )(一定),所以总价和数量成( )比例。
(3)已知5x=3y(x和y均不为0),则x和y成( )比例。
比值
单价
正
正
3.填空题
(4)长方形的长一定,( )和( )成正比例。
(5)一种货物,运走的质量和剩下的质量( )正比例。(填“成”或“不成”)
宽
不成
面积
4.一个化肥厂的生产情况如下表,根据表中数据回答问题。
(1)表中有哪两种相关联的量?
时间和生产量是两种相关联的量。
时间越大,生产量也越大。
4.一个化肥厂的生产情况如下表,根据表中数据回答问题。
(2)表中相关联的两种量成正比例吗?为什么?
时间和生产量成正比例,因为
在判断两种量是否成正比例时,先判断两种量是不是两种相关联的量;再判断这两种量中相对应的两个数的比值是否一定,比值一定,则成正比例,比值不一定,则不成正比例。
