2024北京人大附中高一(下)统练二数学(PDF版含答案)
文档属性
| 名称 | 2024北京人大附中高一(下)统练二数学(PDF版含答案) |  | |
| 格式 | |||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-05 16:45:42 | ||
图片预览



文档简介
高一下数学统练2
2024年4月
姓名:
班级:
考号:
一、单选题(本大题共10小题,每题5分,共50分)
1扇形的半径为2,弧长为行,它的面积为()
A.
π
B.2n
C.
D.2n2
5
5
5
2.若角0的终边经过点(-2,3),则sn(π+0)=()
A.-3
B.-2g
33
13
13
c.
13
D
3.下列函数的最小正周期为π且为奇函数的是()
A.y=cos2x
B.y=tan 2x
C.y=sin x
D.y=cos
+2x
(2
4.、7
B.2
9
C.-2
D.7
3
5.已知△ABC中,“|AB+ACI>|AB-AC|”是“△ABC为锐角三角形”的
()
A充分而不必要条件
B.充分必要条件
C.必要而不充分条件
D.既不充分也不必要条件
6.要得到函数y=sin4x的图像,只需要将函数y=sin
4x-
的图像()
3
A向右平移红个单位
B.向左平移文个单位
12
12
C.向左平移灭个单位
3
D.向右平移”个单位
2
1
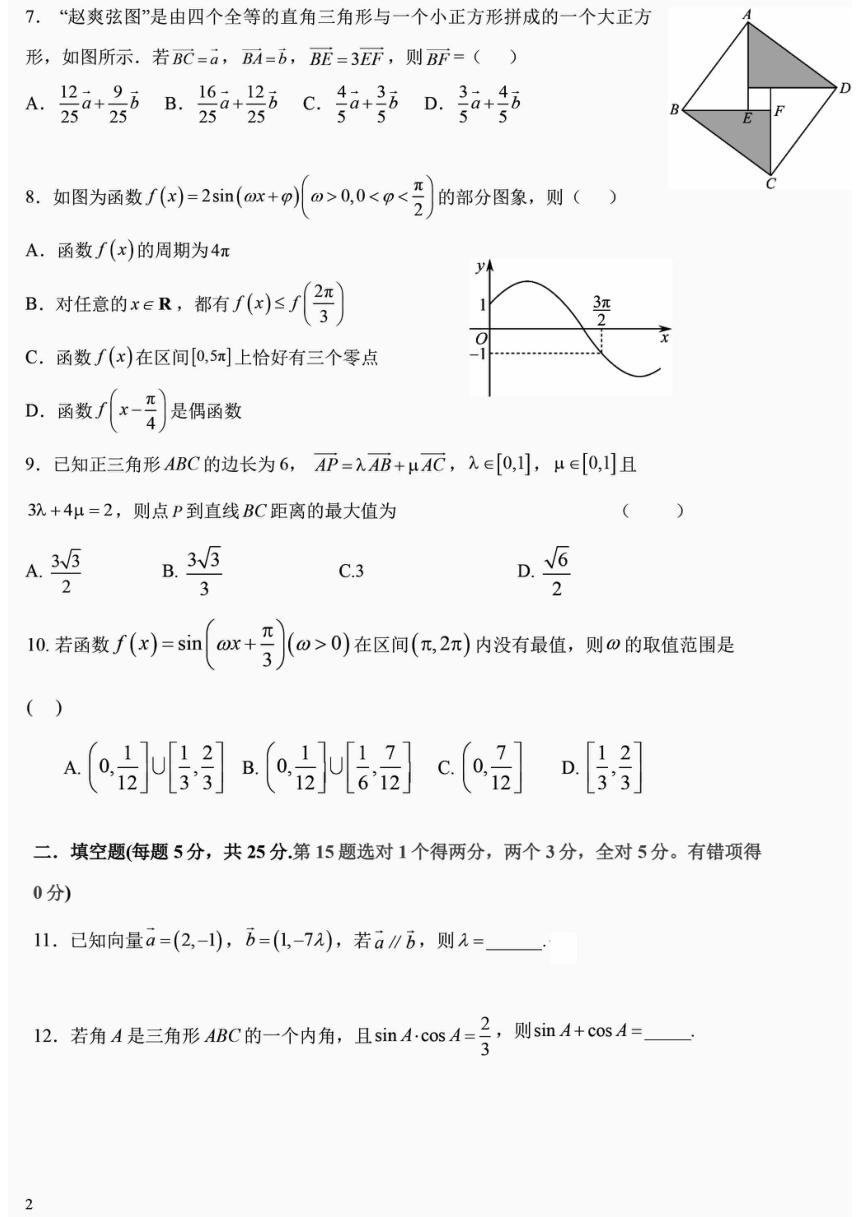
7.“赵爽弦图”是由四个全等的直角三角形与一个小正方形拼成的一个大正方
形,如图所示.若BC=a,BA=b,BE=3EF,则BF=()
A+B.a+5c.6D.0+
25
251
5
5
8.如图为函数f()=2sin(or+po>0,0<<的部分图象,则()
A.函数f(x)的周期为4π
B.对任意的x∈R,都行)s()
3π
0
C.函数f(x)在区问[0,5π]上恰好有三个零点
D.
函数-4
是偶函数
9.已知正三角形ABC的边长为6,AP=入AB+uAC,∈[0,,μ∈[0,且
3入+4μ=2,则点P到直线BC距离的最大值为
A.33
B33
C.3
D.6
2
3
2
10若两数f(y=sm0r+}(@>0)在区间(红,2)内没有授信,则心的取值范阁是
()
〔2[go8c(o引引
二.填空题(每题5分,共25分.第15题选对1个得两分,两个3分,全对5分。有错项得
0分)
11.已知向量a=(2,-1),万=(1,-7),若a∥方,则元=一
12.若角A是三角形ABC的一个内角,且sinA:cosA=名,则simA+cosA=一,
3
2
13.为了研究钟表与三角函数的关系,建立如图所示的平面直角坐标系.设秒针针尖的位置
为P(x,y),若初始位置为
当秒针针尖从P(注:此时t=0)正常开始走
2
时,点P的纵坐标y与时间的函数关系式为
y
w31
P(r,y)
14.记函数.f(x)=sin
x+
4
+b(ω>0)的最小止周期为T.
2r37元
y=f()的图象关于点
2
中心对称,则
1
15.如图,已知△ABC,△DEF均为等边三角形,D,E,F分别为BE,CF,AD的中点,
P为△DEF内一点(含边界).AP=xAB+yAC,下面说法正确的是
①延长BE交AC于M,则CM=CA:
②若OD+OE+OF=0,则O为△ABC的重心:
③若x+y=),则点P的轨迹是一条线段:
E
④若x=,则)的取值范围是
D
F
B
三.解答题(2道答题,共25分)
16.(12分)若平面向量d、b满足a+b=1,b=(-2,-1).
(1)若a+b平行于x轴,求向量a的坐标:
(2)若a=v2,求2a-b的值.
3
2024年4月
姓名:
班级:
考号:
一、单选题(本大题共10小题,每题5分,共50分)
1扇形的半径为2,弧长为行,它的面积为()
A.
π
B.2n
C.
D.2n2
5
5
5
2.若角0的终边经过点(-2,3),则sn(π+0)=()
A.-3
B.-2g
33
13
13
c.
13
D
3.下列函数的最小正周期为π且为奇函数的是()
A.y=cos2x
B.y=tan 2x
C.y=sin x
D.y=cos
+2x
(2
4.、7
B.2
9
C.-2
D.7
3
5.已知△ABC中,“|AB+ACI>|AB-AC|”是“△ABC为锐角三角形”的
()
A充分而不必要条件
B.充分必要条件
C.必要而不充分条件
D.既不充分也不必要条件
6.要得到函数y=sin4x的图像,只需要将函数y=sin
4x-
的图像()
3
A向右平移红个单位
B.向左平移文个单位
12
12
C.向左平移灭个单位
3
D.向右平移”个单位
2
1
7.“赵爽弦图”是由四个全等的直角三角形与一个小正方形拼成的一个大正方
形,如图所示.若BC=a,BA=b,BE=3EF,则BF=()
A+B.a+5c.6D.0+
25
251
5
5
8.如图为函数f()=2sin(or+po>0,0<<的部分图象,则()
A.函数f(x)的周期为4π
B.对任意的x∈R,都行)s()
3π
0
C.函数f(x)在区问[0,5π]上恰好有三个零点
D.
函数-4
是偶函数
9.已知正三角形ABC的边长为6,AP=入AB+uAC,∈[0,,μ∈[0,且
3入+4μ=2,则点P到直线BC距离的最大值为
A.33
B33
C.3
D.6
2
3
2
10若两数f(y=sm0r+}(@>0)在区间(红,2)内没有授信,则心的取值范阁是
()
〔2[go8c(o引引
二.填空题(每题5分,共25分.第15题选对1个得两分,两个3分,全对5分。有错项得
0分)
11.已知向量a=(2,-1),万=(1,-7),若a∥方,则元=一
12.若角A是三角形ABC的一个内角,且sinA:cosA=名,则simA+cosA=一,
3
2
13.为了研究钟表与三角函数的关系,建立如图所示的平面直角坐标系.设秒针针尖的位置
为P(x,y),若初始位置为
当秒针针尖从P(注:此时t=0)正常开始走
2
时,点P的纵坐标y与时间的函数关系式为
y
w31
P(r,y)
14.记函数.f(x)=sin
x+
4
+b(ω>0)的最小止周期为T.
2r
y=f()的图象关于点
2
中心对称,则
1
15.如图,已知△ABC,△DEF均为等边三角形,D,E,F分别为BE,CF,AD的中点,
P为△DEF内一点(含边界).AP=xAB+yAC,下面说法正确的是
①延长BE交AC于M,则CM=CA:
②若OD+OE+OF=0,则O为△ABC的重心:
③若x+y=),则点P的轨迹是一条线段:
E
④若x=,则)的取值范围是
D
F
B
三.解答题(2道答题,共25分)
16.(12分)若平面向量d、b满足a+b=1,b=(-2,-1).
(1)若a+b平行于x轴,求向量a的坐标:
(2)若a=v2,求2a-b的值.
3
同课章节目录
