三年级上册数学青岛版分数的大小比较(课件)(共24张PPT)
文档属性
| 名称 | 三年级上册数学青岛版分数的大小比较(课件)(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 779.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-05 18:15:22 | ||
图片预览







文档简介
(共24张PPT)
分数的大小比较
课 前 练 习
1.在括号内填上适当的整数:
6
6
4
25
课 前 练 习
2.在下面的( )里填上“<”,“>”或“=”
问:通过以上的比较,你能得到什么规律?
同分母看分子,分子大的分数较____。
同分子看分母,分母大的分数较____。
>
<
>
<
大
小
讨论:
3
4
5
6
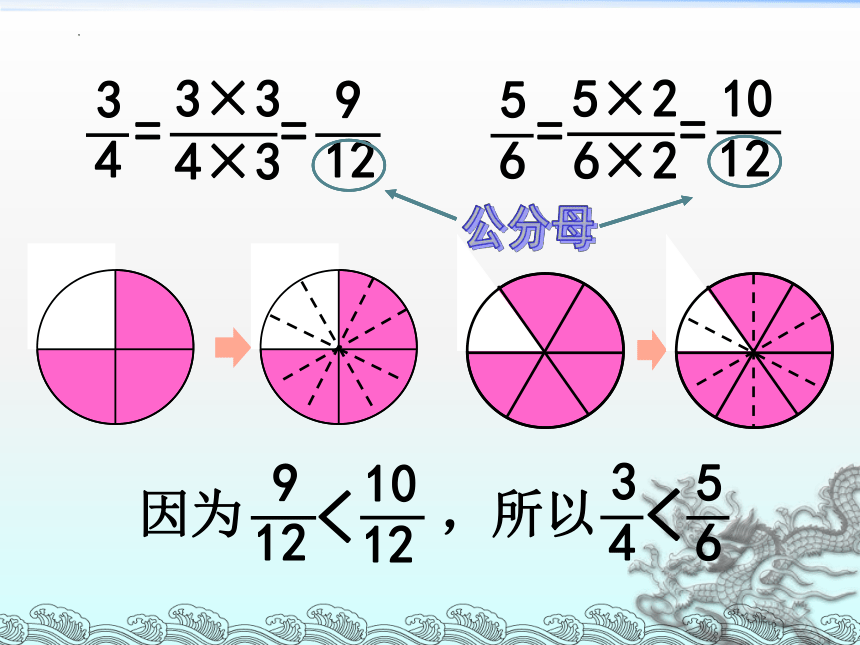
3
4
=
3×3
4×3
=
9
12
5
6
=
5×2
6×2
=
10
12
公分母
公分母
公分母
因为
9
12
<
10
12
,所以
3
4
<
5
6
电缆线的直径为 厘米。管道内径为 厘米。电缆线是否可以穿进管道?
思考
我们可以转化为怎样的一个数学问题来解决这个实际问题?
比较 和 的大小。
想一想你有哪些方法?
0
1
0
1
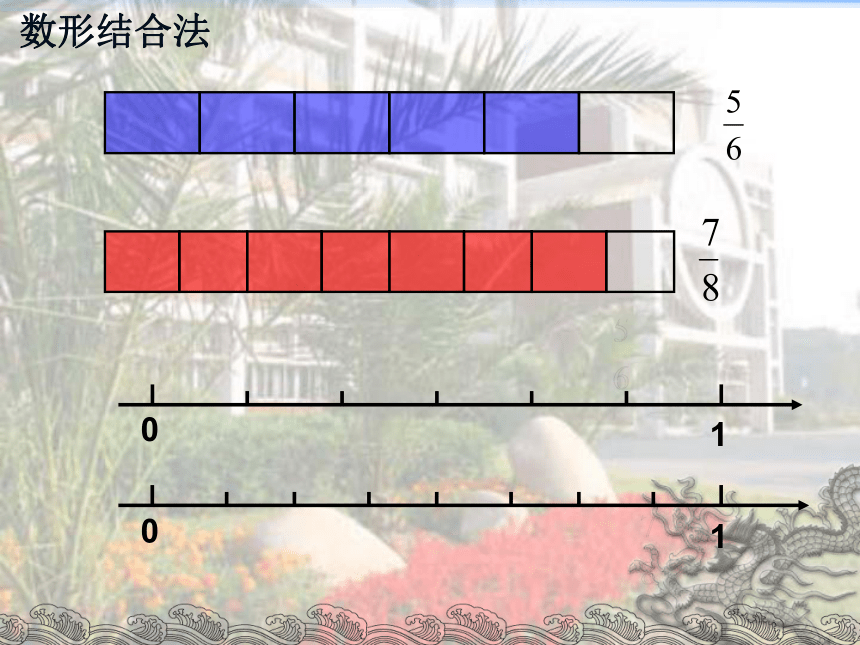
数形结合法
想一想:如果要把 和 化成同分母的分数,
分母必须取什么样的数?
分母必须是6和8的公倍数,这个分母叫做公分母.
6和8的公倍数有24,48,72,96,···等,取几比较恰当?
一般取它们的最小公倍数,这里就取24作为它们的公分母.
我们知道:
像这样,将异分母的分数分别化成与原分数大小相等的同分母的分数,这个过程叫做通分。
想一想:通分的依据是什么?
因为 ,
所以 .
分数的基本性质
例1:将下列每组两个分数通分,并比较大小。
(1) 和
(2) 和
例2:把 , 和 通分,并比较它们的大小。
想一想:分数的通分和约分有什么不同?
1.把下列每组中的两个分数通分,并比较它们的大小:
(1) 和
(3) 和
(2) 和
(4) 和
课堂检测
课堂检测
2.把 、 和 进行通分,并按从小到大
的顺序排列:
课堂小结
1.通分:将异分母的分数分别化成与原分数大小相等的同分母的分数,这个过程叫做通分。
(1)通分的依据是分数的基本性质。
(2)通分时,公分母有无数多个,比较恰当的是找各分母的最小公倍数。
注意通分与约分的差异。
2.利用通分将异分母的分数化成同分母的分数比较大小。
拓 展 练 习
1.比 大但比 小的最简分数有____个,请你写出两个:____________;
2.求使 成立的 的最小正整数;
3.甲、乙两名工人展开劳动竞赛,甲15分钟做了25个零件;乙12分钟做了16个零件,那么谁的加工速度较快?为什么?
求下列每组数的最小公倍数。
6和9
10和11
7和49
6和9
6 9
3
3
3
×
3=
2
×
18
2
比较下列每组分数的大小。
3
5
3
6
4
7
5
7
3
4
5
6
把下面每组中的两个分数通分。
2
3
和
1
4
1
6
和
7
12
3
10
和
8
15
3
8
和
、
2
3
1
4
下面哪组分数的通分是对的?哪组不对?哪组不够简单?
3
4
=
15
20
3
5
=
15
20
1、
5
6
=
30
36
4
9
=
16
36
2、
7
8
=
21
24
5
6
=
20
24
3、
√
15
18
8
18
12
20
三名学生跳远的成绩是:
甲 4 米,
乙 4 米,
丙 4 米,
谁是第一名?谁是第三名?
3
8
4
9
1
3
下面的五个分数排列得对不对?如果不对,应该怎样排列?
2
3
5
6
7
8
16
17
17
25
<
<
<
<
思考:
谢谢聆听
分数的大小比较
课 前 练 习
1.在括号内填上适当的整数:
6
6
4
25
课 前 练 习
2.在下面的( )里填上“<”,“>”或“=”
问:通过以上的比较,你能得到什么规律?
同分母看分子,分子大的分数较____。
同分子看分母,分母大的分数较____。
>
<
>
<
大
小
讨论:
3
4
5
6
3
4
=
3×3
4×3
=
9
12
5
6
=
5×2
6×2
=
10
12
公分母
公分母
公分母
因为
9
12
<
10
12
,所以
3
4
<
5
6
电缆线的直径为 厘米。管道内径为 厘米。电缆线是否可以穿进管道?
思考
我们可以转化为怎样的一个数学问题来解决这个实际问题?
比较 和 的大小。
想一想你有哪些方法?
0
1
0
1
数形结合法
想一想:如果要把 和 化成同分母的分数,
分母必须取什么样的数?
分母必须是6和8的公倍数,这个分母叫做公分母.
6和8的公倍数有24,48,72,96,···等,取几比较恰当?
一般取它们的最小公倍数,这里就取24作为它们的公分母.
我们知道:
像这样,将异分母的分数分别化成与原分数大小相等的同分母的分数,这个过程叫做通分。
想一想:通分的依据是什么?
因为 ,
所以 .
分数的基本性质
例1:将下列每组两个分数通分,并比较大小。
(1) 和
(2) 和
例2:把 , 和 通分,并比较它们的大小。
想一想:分数的通分和约分有什么不同?
1.把下列每组中的两个分数通分,并比较它们的大小:
(1) 和
(3) 和
(2) 和
(4) 和
课堂检测
课堂检测
2.把 、 和 进行通分,并按从小到大
的顺序排列:
课堂小结
1.通分:将异分母的分数分别化成与原分数大小相等的同分母的分数,这个过程叫做通分。
(1)通分的依据是分数的基本性质。
(2)通分时,公分母有无数多个,比较恰当的是找各分母的最小公倍数。
注意通分与约分的差异。
2.利用通分将异分母的分数化成同分母的分数比较大小。
拓 展 练 习
1.比 大但比 小的最简分数有____个,请你写出两个:____________;
2.求使 成立的 的最小正整数;
3.甲、乙两名工人展开劳动竞赛,甲15分钟做了25个零件;乙12分钟做了16个零件,那么谁的加工速度较快?为什么?
求下列每组数的最小公倍数。
6和9
10和11
7和49
6和9
6 9
3
3
3
×
3=
2
×
18
2
比较下列每组分数的大小。
3
5
3
6
4
7
5
7
3
4
5
6
把下面每组中的两个分数通分。
2
3
和
1
4
1
6
和
7
12
3
10
和
8
15
3
8
和
、
2
3
1
4
下面哪组分数的通分是对的?哪组不对?哪组不够简单?
3
4
=
15
20
3
5
=
15
20
1、
5
6
=
30
36
4
9
=
16
36
2、
7
8
=
21
24
5
6
=
20
24
3、
√
15
18
8
18
12
20
三名学生跳远的成绩是:
甲 4 米,
乙 4 米,
丙 4 米,
谁是第一名?谁是第三名?
3
8
4
9
1
3
下面的五个分数排列得对不对?如果不对,应该怎样排列?
2
3
5
6
7
8
16
17
17
25
<
<
<
<
思考:
谢谢聆听
