27.2.1 相似三角形的判定 学习任务单(无答案、2课时)2023-2024学年人教版九年级数学下册
文档属性
| 名称 | 27.2.1 相似三角形的判定 学习任务单(无答案、2课时)2023-2024学年人教版九年级数学下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 68.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-06 14:39:07 | ||
图片预览

文档简介
学习任务单
课程基本信息
学科 初中数学 年级 九 学期 春季
课题 相似三角形的判定
教科书 书 名:人教版教材 出版社:人民教育出版社
学习目标
1.掌握相似三角形的定义及表示。 2.掌握平行线分线段成比例定理及其推论。 3.掌握并能用应用平行线分线段成比例定理的推论判定三角形相似。
课前学习任务
1. 复习相似多边形。 2. 复习全等三角形的判定。
课上学习任务
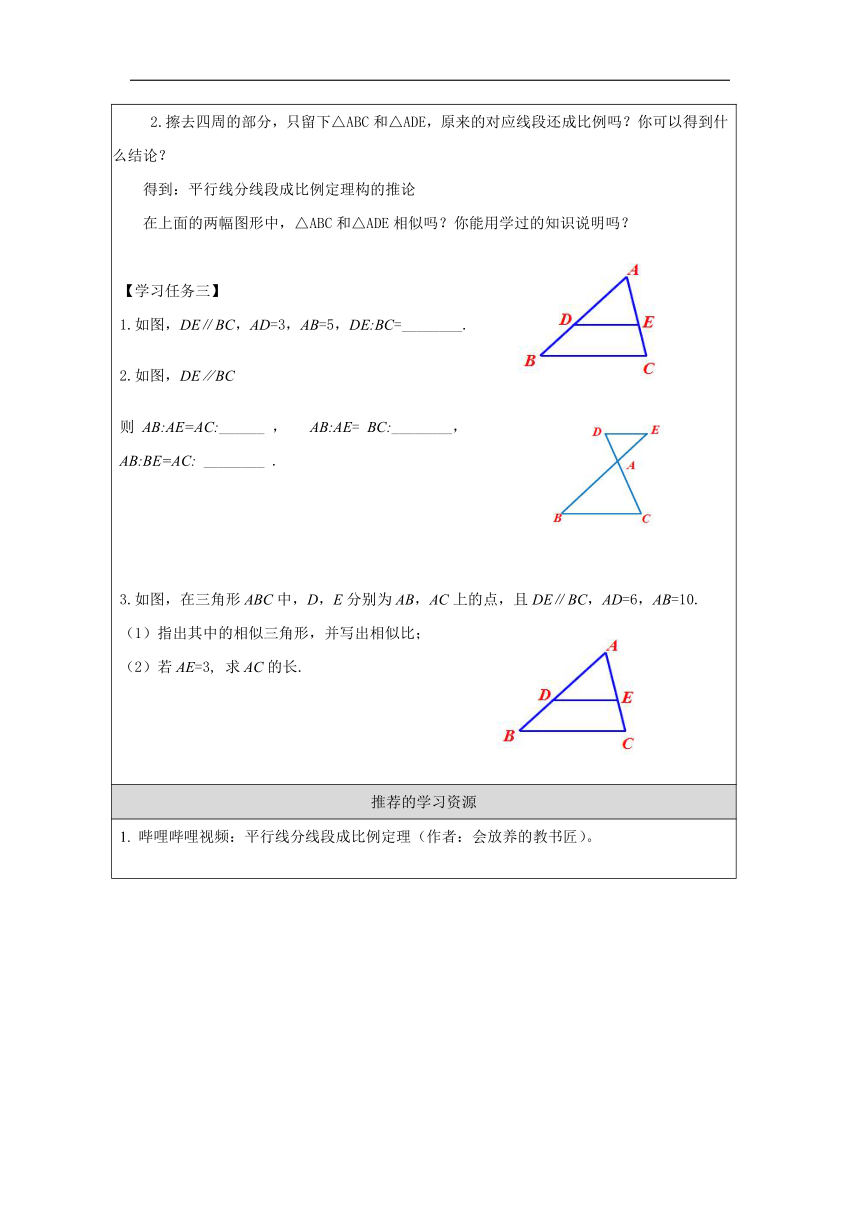
【学习任务一】 教材29页探究 平行线分线段成比例定理 思考: 1.线段AB,BC,DE,EF的长度随着直线的位置的变化而变化吗? 2.猜测与相等吗? 3.通过画图,测量,计算验证你的猜想. 4.用数学语言描述你的发现. 【学习任务二】 思考并完成 1.定理图形中的直线交点在直线上时,对应线段还成比例吗? 2.擦去四周的部分,只留下△ABC和△ADE,原来的对应线段还成比例吗?你可以得到什么结论? 得到:平行线分线段成比例定理构的推论 在上面的两幅图形中,△ABC和△ADE相似吗?你能用学过的知识说明吗? 【学习任务三】 1.如图,DE∥BC,AD=3,AB=5,DE:BC=________. 2.如图,DE∥BC 则 AB:AE=AC:______ , AB:AE= BC:________, AB:BE=AC: ________ . 3.如图,在三角形ABC中,D,E分别为AB,AC上的点,且DE∥BC,AD=6,AB=10. (1)指出其中的相似三角形,并写出相似比; (2)若AE=3, 求AC的长.
推荐的学习资源
1. 哔哩哔哩视频:平行线分线段成比例定理(作者:会放养的教书匠)。
学习任务单
课程基本信息
学科 初中数学 年级 九 学期 春季
课题 相似三角形的判定(第二课时)
教科书 书 名:人教版教材 出版社:人民教育出版社 出版日期:2022年4月
学习目标
1.掌握三边对应成比例的两个三角形相似的判定定理。 2.掌握两组对应边的比相等且它们的夹角相等的两个三角形相似的判定定理。 3.掌握用两个角对应相等判定三角形相似的方法。
课前学习任务
1. 复习相似三角形的判定方法:定义和平行线法。 2. 预习相似三角形的判定方法。
课上学习任务
【学习任务一】 探究三边成比例的两个三角形相似 (一)画图探究: 1.任意画一个三角形. 2.再画一个三角形,使它的各边长都是原来三角形 各边长的 k 倍. 3. 比较它们的对应角相等吗? 4. 这两个三角形相似吗? (二)尝试用几何语言描述猜想 (三)尝试证明 【学习任务二】 探究对应边的比相等,且它们的夹角相等的两个三角形相似 用上面的方法证明 已知:如图,△A'B'C'和△ABC中,∠A'=∠A, A'B':AB=A'C':AC, 求证:△A'B'C'∽△ABC. 【学习任务三】 探究两个角相等的两个三角形相似 (一)观察、思考与尝试 1.观察两幅三角板(大小不同),它们看起来形状分别一样吗 相似吗 2.猜测任意一对三角形如果有两个角对应相等,它们相似吗?用什么方法来判断? 3.通过画图,测量,计算,验证你的猜想. 4.用数学语言描述你的发现. 5.和周围同学交流一下,你们的结论一样吗 尝试类比三边判定方法证明. (二)尝试证明 【学习任务四】 例1:根据下列条件,判断△ABC与△A′B′C′是否相似,并说明理由: (1)AB=4cm,BC=6cm,AC=8cm;A′B′=12cm,B′C′=18cm,A′C′=24cm; (2)∠A=120°,AB=7cm,AC=14cm, ∠A'=120°,A′B′=3cm,A′C′=6cm. 例2、如图,在 Rt△ABC 中,∠C = 90°,AB = 10,AC = 8. E 是 AC 上一点,AE = 5,ED⊥AB,垂足为D. 求AD的长. 拓展巩固:如图,在 Rt△ABC 和 Rt△A'B'C'中,∠C=90°,∠C′=90°, . 求证:Rt△ABC ∽Rt△A'B'C'.
课程基本信息
学科 初中数学 年级 九 学期 春季
课题 相似三角形的判定
教科书 书 名:人教版教材 出版社:人民教育出版社
学习目标
1.掌握相似三角形的定义及表示。 2.掌握平行线分线段成比例定理及其推论。 3.掌握并能用应用平行线分线段成比例定理的推论判定三角形相似。
课前学习任务
1. 复习相似多边形。 2. 复习全等三角形的判定。
课上学习任务
【学习任务一】 教材29页探究 平行线分线段成比例定理 思考: 1.线段AB,BC,DE,EF的长度随着直线的位置的变化而变化吗? 2.猜测与相等吗? 3.通过画图,测量,计算验证你的猜想. 4.用数学语言描述你的发现. 【学习任务二】 思考并完成 1.定理图形中的直线交点在直线上时,对应线段还成比例吗? 2.擦去四周的部分,只留下△ABC和△ADE,原来的对应线段还成比例吗?你可以得到什么结论? 得到:平行线分线段成比例定理构的推论 在上面的两幅图形中,△ABC和△ADE相似吗?你能用学过的知识说明吗? 【学习任务三】 1.如图,DE∥BC,AD=3,AB=5,DE:BC=________. 2.如图,DE∥BC 则 AB:AE=AC:______ , AB:AE= BC:________, AB:BE=AC: ________ . 3.如图,在三角形ABC中,D,E分别为AB,AC上的点,且DE∥BC,AD=6,AB=10. (1)指出其中的相似三角形,并写出相似比; (2)若AE=3, 求AC的长.
推荐的学习资源
1. 哔哩哔哩视频:平行线分线段成比例定理(作者:会放养的教书匠)。
学习任务单
课程基本信息
学科 初中数学 年级 九 学期 春季
课题 相似三角形的判定(第二课时)
教科书 书 名:人教版教材 出版社:人民教育出版社 出版日期:2022年4月
学习目标
1.掌握三边对应成比例的两个三角形相似的判定定理。 2.掌握两组对应边的比相等且它们的夹角相等的两个三角形相似的判定定理。 3.掌握用两个角对应相等判定三角形相似的方法。
课前学习任务
1. 复习相似三角形的判定方法:定义和平行线法。 2. 预习相似三角形的判定方法。
课上学习任务
【学习任务一】 探究三边成比例的两个三角形相似 (一)画图探究: 1.任意画一个三角形. 2.再画一个三角形,使它的各边长都是原来三角形 各边长的 k 倍. 3. 比较它们的对应角相等吗? 4. 这两个三角形相似吗? (二)尝试用几何语言描述猜想 (三)尝试证明 【学习任务二】 探究对应边的比相等,且它们的夹角相等的两个三角形相似 用上面的方法证明 已知:如图,△A'B'C'和△ABC中,∠A'=∠A, A'B':AB=A'C':AC, 求证:△A'B'C'∽△ABC. 【学习任务三】 探究两个角相等的两个三角形相似 (一)观察、思考与尝试 1.观察两幅三角板(大小不同),它们看起来形状分别一样吗 相似吗 2.猜测任意一对三角形如果有两个角对应相等,它们相似吗?用什么方法来判断? 3.通过画图,测量,计算,验证你的猜想. 4.用数学语言描述你的发现. 5.和周围同学交流一下,你们的结论一样吗 尝试类比三边判定方法证明. (二)尝试证明 【学习任务四】 例1:根据下列条件,判断△ABC与△A′B′C′是否相似,并说明理由: (1)AB=4cm,BC=6cm,AC=8cm;A′B′=12cm,B′C′=18cm,A′C′=24cm; (2)∠A=120°,AB=7cm,AC=14cm, ∠A'=120°,A′B′=3cm,A′C′=6cm. 例2、如图,在 Rt△ABC 中,∠C = 90°,AB = 10,AC = 8. E 是 AC 上一点,AE = 5,ED⊥AB,垂足为D. 求AD的长. 拓展巩固:如图,在 Rt△ABC 和 Rt△A'B'C'中,∠C=90°,∠C′=90°, . 求证:Rt△ABC ∽Rt△A'B'C'.
