北师大版小学数学六年级下册4.2《正比例》同步练习(含答案)
文档属性
| 名称 | 北师大版小学数学六年级下册4.2《正比例》同步练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 254.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-05 20:28:29 | ||
图片预览




文档简介
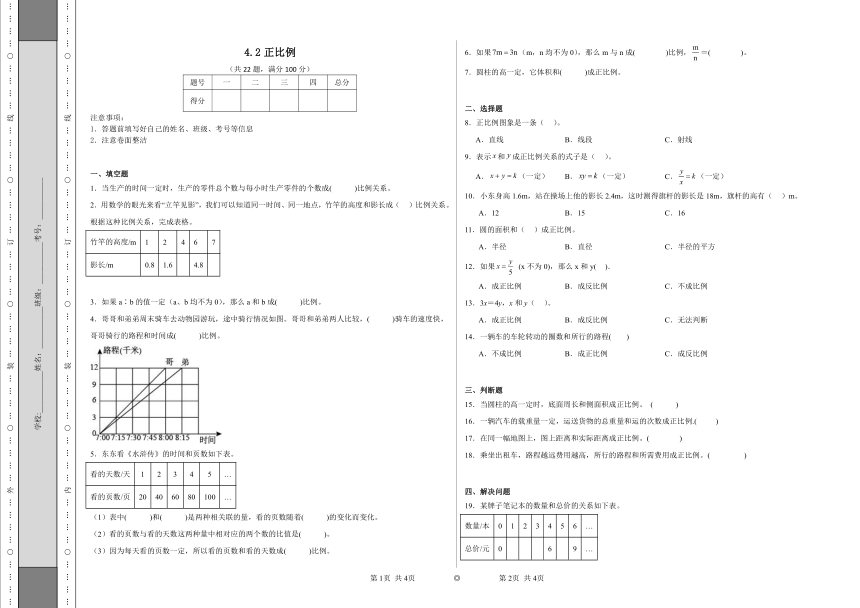
4.2正比例
(共22题,满分100分)
题号 一 二 三 四 总分
得分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.注意卷面整洁
一、填空题
1.当生产的时间一定时,生产的零件总个数与每小时生产零件的个数成( )比例关系。
2.用数学的眼光来看“立竿见影”,我们可以知道同一时间、同一地点,竹竿的高度和影长成( )比例关系。根据这种比例关系,完成表格。
竹竿的高度/m 1 2 4 6 7
影长/m 0.8 1.6 4.8
3.如果a∶b的值一定(a、b均不为0),那么a和b成( )比例。
4.哥哥和弟弟周末骑车去动物园游玩,途中骑行情况如图。哥哥和弟弟两人比较,( )骑车的速度快,哥哥骑行的路程和时间成( )比例。
5.东东看《水浒传》的时间和页数如下表。
看的天数/天 1 2 3 4 5 …
看的页数/页 20 40 60 80 100 …
(1)表中( )和( )是两种相关联的量,看的页数随着( )的变化而变化。
(2)看的页数与看的天数这两种量中相对应的两个数的比值是( )。
(3)因为每天看的页数一定,所以看的页数和看的天数成( )比例。
6.如果(m,n均不为0),那么m与n成( )比例,=( )。
7.圆柱的高一定,它体积和( )成正比例。
二、选择题
8.正比例图象是一条( )。
A.直线 B.线段 C.射线
9.表示和成正比例关系的式子是( )。
A.(一定) B.(一定) C.(一定)
10.小东身高1.6m,站在操场上他的影长2.4m,这时测得旗杆的影长是18m,旗杆的高有( )m。
A.12 B.15 C.16
11.圆的面积和( )成正比例。
A.半径 B.直径 C.半径的平方
12.如果 (x不为0),那么x和y( ).
A.成正比例 B.成反比例 C.不成比例
13.3x=4y,x和y( )。
A.成正比例 B.成反比例 C.无法判断
14.一辆车的车轮转动的圈数和所行的路程( )
A.不成比例 B.成正比例 C.成反比例
三、判断题
15.当圆柱的高一定时,底面周长和侧面积成正比例。 ( )
16.一辆汽车的载重量一定,运送货物的总重量和运的次数成正比例.( )
17.在同一幅地图上,图上距离和实际距离成正比例。( )
18.乘坐出租车,路程越远费用越高,所行的路程和所需费用成正比例。( )
四、解决问题
19.某牌子笔记本的数量和总价的关系如下表。
数量/本 0 1 2 3 4 5 6 …
总价/元 0 6 9 …
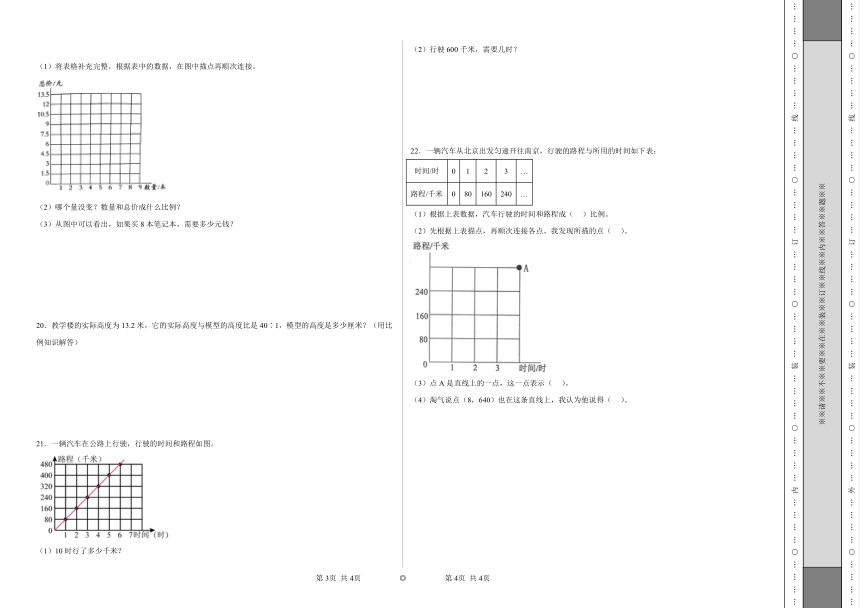
(1)将表格补充完整,根据表中的数据,在图中描点再顺次连接。
(2)哪个量没变?数量和总价成什么比例?
(3)从图中可以看出,如果买8本笔记本,需要多少元钱?
20.教学楼的实际高度为13.2米,它的实际高度与模型的高度比是40∶1,模型的高度是多少厘米?(用比例知识解答)
21.一辆汽车在公路上行驶,行驶的时间和路程如图。
(1)10时行了多少千米?
(2)行驶600千米,需要几时?
22.一辆汽车从北京出发匀速开往南京,行驶的路程与所用的时间如下表:
时间/时 0 1 2 3 …
路程/千米 0 80 160 240 …
(1)根据上表数据,汽车行驶的时间和路程成( )比例。
(2)先根据上表描点,再顺次连接各点。我发现所描的点( )。
(3)点A是直线上的一点,这一点表示( )。
(4)淘气说点(8,640)也在这条直线上,我认为他说得( )。
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
) (
学校:___________姓名:___________班级:___________考号:___________
) (
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
第1页 共4页 ◎ 第2页 共4页
第1页 共4页 ◎ 第2页 共4页
参考答案:
1.正
【解析】略
2.正;3.2;5.6
【分析】
判断两个相关联的量之间成什么比例,就看这个量是对应的比值一定,还是对应的乘积一定;如果比值一定,就成正比例;如果是乘积一定,则成反比例。同一时刻,不同物体的实际高度和它的影长的比值一定的,即物体的实际高度和它的影长成正比例。题目中竹竿的高度和竿影的长度的比值是一定的,代入统计表的数据,即可完成空格里的内容。
【详解】
同一时间,同一地点,竹竿的高和竿影的长成正比例。
4÷1.25=3.2(米)
7÷1.25=5.6(米)
竹竿的高度/m 1 2 4 6 7
影长/m 0.8 1.6 3.2 4.8 5.6
3.正
【分析】相对应的两个量x和y的比值一定,即=k(定值),那么这两个量叫做成正比例的量,它们的关系叫做正比例关系;据此解答。
【详解】根据正比例的意义可得:如果a∶b的值一定(a、b均不为0),那么a和b成正比例。
故答案为:正
【点睛】本题主要考查正比例的意义,解题时要明确相关联的两种量若比值一定,就成正比例。
4. 哥哥 正
【分析】(1)哥哥和弟弟骑得距离一样,只要比较谁花的时间少,就知道谁骑车的速度快。
(2)判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【详解】(1)观察图可知:哥哥和弟弟两人都行了12千米,哥哥用的时间少,所以哥哥骑车的速度快;
(2)因为路程∶时间=速度(一定),是比值一定,所以哥哥骑行的路程和时间成正比例。
【点睛】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
5. 页数 天数 天数 20 正
【分析】(1)上表中,表格中是页数和天数两种相关联的量,看的页数的多少是随着天数的变化而变化的;
(2)看的页数与天数这两种量中相对应的两个数的比值,即页数÷天数;
(3)因为页数÷天数=每天看的页数,所以每天看的页数,即比值一定,所以看的页数与看的天数成正比例,据此解答。
【详解】(1)表格中的页数和天数是两种相关联的量,看的页数的多少是随着天数的变化而变化的;
(2)看的页数与看的天数这两种量中相对应的两个数的比值是20∶1=40∶2=20;
(3)因为每天看的页数一定,所以看的页数与看的天数成正比例关系。
【点睛】本题重在考查比的意义、求比值以及正比例、反比例关系的判断方法。
6. 正
【分析】根据比例的基本性质:内项积=外项积,即m∶n=3∶7,由于3∶7=3÷7=,所以m和n的比值一定,根据正比例的判定方法:当两个相关联的量比值一定,则成正比例关系,据此即可填空。
【详解】由于m∶n=3∶7
则m∶n=3÷7=,即=
如果7m=3n(m,n均不为0),那么m与n成正比例,=。
【点睛】本题主要考查比例的基本性质以及正比例的意义,熟练掌握正比例的意义是解题的关键。
7.底面积
【分析】判断体积和底面积、半径、周长是否成比例,就看这两种量是否是对应的乘积(商)一定,如果是乘积(商)一定,就成反(正)比例,如果不是乘积(商)一定或乘积(商)不一定,就不成比例。
【详解】因为:圆柱的体积÷底面积=高(一定)也就是圆柱的体积与底面积的商一定,符合正比例的意义,所以圆柱的体积与底面积成正比例
【点睛】此题考查用正反比例的意义辨识成正比例的量与成反比例的量。
8.A
【分析】两种相关联的量中相对应的两个数的商一定,就成正比例关系,正比例的图象是一条过原点的直线。
【详解】由分析可知;正比例图象是一条直线。
故答案为:A
【点睛】本题考查了对正比例图象的认识,属于基础知识。
9.C
【分析】根据(一定),x和y成正比例关系,进行选择。
【详解】A. (一定),x和y不成比例关系;
B. (一定),x和y成反比例关系;
C. (一定),x和y成正比例关系。
故答案为:C
【点睛】本题考查了辨识正比例的量,商一定是正比例关系,积一定是反比例关系。
10.A
【解析】略
11.C
【分析】根据“两个相关联的量,一个量变化,另一个量也随着变化,如果相对应的两个量x和y的比值一定,即=k(定值),那么这两个量叫做成正比例的量,它们的关系叫做正比例关系。”解答即可。
【详解】A、因为圆的面积÷半径=圆周率×半径(不一定),所以圆的面积和半径不成正比例,不符合题意;
B、因为圆的面积÷直径=圆周率×半径÷2(不一定),所以圆的面积和直径不成正比例,不符合题意;
C、因为圆的面积÷半径的平方=圆周率(一定),所以圆的面积和半径的平方成正比例,符合题意;
故答案为:C
【点睛】本题主要考查正比例关系的辨识,牢记圆的面积公式及正比例的意义是解题的关键。
12.A
【详解】略
13.A
【分析】根据数量关系判断出x和y的商一定还是乘积一定,如果商一定就成正比例,如果乘积一定就成反比例,否则不成比例。
【详解】因为3x=4y,所以x÷y=,x和y的商一定,二者成正比例。
故答案为:A
【点睛】本题考查正反比例的辨别,掌握正反比例的定义就能解决问题。
14.B
【详解】略
15.√
【详解】当圆柱的高一定时,即圆柱的底面周长和侧面积的商一定,所以底面周长和侧面积成正比例关系。
所以原题说法正确。
16.√
【分析】根据数量关系判断运货总重量与运的次数的商一定还是积一定,如果商一定就成正比例,如果积一定就成反比例,否则不成比例.
【详解】货物总重量÷运货的次数=一辆车的载重量,载重量一定,货物总重量与运货的次数的商一定,二者成正比例,原题说法正确.
故答案为正确
17.√
【详解】图上距离∶实际距离=比例尺,图上距离和实际距离的比值一定,二者成正比例。
故答案为:√
18.×
【分析】判断两个相关联的量之间成不成正比例,就看这两个量对应的数的比值是否一定。如果比值一定,就成正比例。据此即可解答。
【详解】因为出租车车票的价格=起步价+超过起步价的公里数×超过起步价公里数每行1千米所需要的钱数。所以所行的路程和所需费用不成正比例。
故答案为:×
【点睛】本题考查学生对成正比例的量知识的掌握。
19.(1)1.5;3;4.5;7.5
画图如下:
(2)单价没变,数量和总价成正比例。
(3)需要12元钱。
【分析】(1)根据总价÷数量=单价,求出单价,再根据单价×数量=总价,求出各自对应的总价;最后描点连线即可;
(2)根据总价、数量、单价之间的关系解答即可;
(3)根据根据总价÷数量=单价,求出单价,再根据单价×数量=总价,即可求出对应的总价。
【详解】(1)6÷4=1.5(元)
1.5×1=1.5(元)
1.5×2=3(元)
1.5×3=4.5(元)
1.5×5=7.5(元)
填表、画图如下:
数量/本 0 1 2 3 4 5 6 …
总价/元 0 1.5 3 4.5 6 7.5 9 …
(2)总价÷数量=单价(比值一定)即单价没变,所以数量和总价成正比例。
(3)6÷4×8
=1.5×8
=12(元)
答:买8本笔记本,需要12元。
【点睛】本题是一道基础题,主要考查单价、数量、总价的关系及正比例的意义。
20.33厘米
【分析】根据教学楼的实际高度与模型高度的比值是一定,即两种量成正比例;13.2米=1320厘米;设模型的高度是x厘米,列比例:40∶1=1320∶x,解比例,即可解答。
【详解】13.2米=1320厘米
解:设模型的高度是x厘米。
40∶1=1320∶x
40x=1×1320
x=1320÷40
x=33
答:模型的高度是33厘米。
【点睛】本题主要考查对正比例的意义的运用:两种相关联的量,一种量变化,另一种量也随着变化,但两种量的相对应的比值一定,这两种量成正比例;注意单位名数的统一。
21.(1)800千米
(2)7.5时
【分析】(1)根据图示可知,这辆车速度不变,路程乙时间成正比例,所以1小时行80千米,10小时行80×10千米;
(2)根据题意利用公式:时间=路程÷速度进行解答。
【详解】(1)80×10=800(千米)
答:10时行了800千米。
(2)600÷80=7.5(小时)
答:行驶600千米,需要7.5时。
【点睛】本题主要考查单式折线统计图,关键根据统计图找对解决问题的条件,利用路程、速度和时间之间的关系做题。
22.(1)正
(2)如图:
在同一条直线上
(3)(4,320)
(4)对
【分析】(1)两个相关联的量,乘积一定成反比例,比值一定成正比例,否则不成比例,据此分析即可;
(2)由图可知横轴表示时间,竖轴表示路程,根据表格数据描点、连线,观察即可;
(3)A点所对应的时间是4时,根据时间及比值,即可求出路程;
(4)求出640与8的比值,与其他比值相同则在这条直线上,据此解答即可。
【详解】(1)80∶1=80
160∶2=80
240∶3=80
80=80=80
则汽车行驶的时间和路程成正比例。
(2)如图:
我发现所描的点在同一条直线上。
(3)4×80=320(千米)
则点A是直线上的一点,这一点表示(4,320)。
(4)640∶8=80
则点(8,640)也在这条直线上,我认为他说得对。
【点睛】本题考查正比例的判断,解题的关键是明确:比值一定的两个量是成正比例关系的量,对应的各点都在同一条直线上。
答案第1页,共2页
答案第1页,共2页
(共22题,满分100分)
题号 一 二 三 四 总分
得分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.注意卷面整洁
一、填空题
1.当生产的时间一定时,生产的零件总个数与每小时生产零件的个数成( )比例关系。
2.用数学的眼光来看“立竿见影”,我们可以知道同一时间、同一地点,竹竿的高度和影长成( )比例关系。根据这种比例关系,完成表格。
竹竿的高度/m 1 2 4 6 7
影长/m 0.8 1.6 4.8
3.如果a∶b的值一定(a、b均不为0),那么a和b成( )比例。
4.哥哥和弟弟周末骑车去动物园游玩,途中骑行情况如图。哥哥和弟弟两人比较,( )骑车的速度快,哥哥骑行的路程和时间成( )比例。
5.东东看《水浒传》的时间和页数如下表。
看的天数/天 1 2 3 4 5 …
看的页数/页 20 40 60 80 100 …
(1)表中( )和( )是两种相关联的量,看的页数随着( )的变化而变化。
(2)看的页数与看的天数这两种量中相对应的两个数的比值是( )。
(3)因为每天看的页数一定,所以看的页数和看的天数成( )比例。
6.如果(m,n均不为0),那么m与n成( )比例,=( )。
7.圆柱的高一定,它体积和( )成正比例。
二、选择题
8.正比例图象是一条( )。
A.直线 B.线段 C.射线
9.表示和成正比例关系的式子是( )。
A.(一定) B.(一定) C.(一定)
10.小东身高1.6m,站在操场上他的影长2.4m,这时测得旗杆的影长是18m,旗杆的高有( )m。
A.12 B.15 C.16
11.圆的面积和( )成正比例。
A.半径 B.直径 C.半径的平方
12.如果 (x不为0),那么x和y( ).
A.成正比例 B.成反比例 C.不成比例
13.3x=4y,x和y( )。
A.成正比例 B.成反比例 C.无法判断
14.一辆车的车轮转动的圈数和所行的路程( )
A.不成比例 B.成正比例 C.成反比例
三、判断题
15.当圆柱的高一定时,底面周长和侧面积成正比例。 ( )
16.一辆汽车的载重量一定,运送货物的总重量和运的次数成正比例.( )
17.在同一幅地图上,图上距离和实际距离成正比例。( )
18.乘坐出租车,路程越远费用越高,所行的路程和所需费用成正比例。( )
四、解决问题
19.某牌子笔记本的数量和总价的关系如下表。
数量/本 0 1 2 3 4 5 6 …
总价/元 0 6 9 …
(1)将表格补充完整,根据表中的数据,在图中描点再顺次连接。
(2)哪个量没变?数量和总价成什么比例?
(3)从图中可以看出,如果买8本笔记本,需要多少元钱?
20.教学楼的实际高度为13.2米,它的实际高度与模型的高度比是40∶1,模型的高度是多少厘米?(用比例知识解答)
21.一辆汽车在公路上行驶,行驶的时间和路程如图。
(1)10时行了多少千米?
(2)行驶600千米,需要几时?
22.一辆汽车从北京出发匀速开往南京,行驶的路程与所用的时间如下表:
时间/时 0 1 2 3 …
路程/千米 0 80 160 240 …
(1)根据上表数据,汽车行驶的时间和路程成( )比例。
(2)先根据上表描点,再顺次连接各点。我发现所描的点( )。
(3)点A是直线上的一点,这一点表示( )。
(4)淘气说点(8,640)也在这条直线上,我认为他说得( )。
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
) (
学校:___________姓名:___________班级:___________考号:___________
) (
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
第1页 共4页 ◎ 第2页 共4页
第1页 共4页 ◎ 第2页 共4页
参考答案:
1.正
【解析】略
2.正;3.2;5.6
【分析】
判断两个相关联的量之间成什么比例,就看这个量是对应的比值一定,还是对应的乘积一定;如果比值一定,就成正比例;如果是乘积一定,则成反比例。同一时刻,不同物体的实际高度和它的影长的比值一定的,即物体的实际高度和它的影长成正比例。题目中竹竿的高度和竿影的长度的比值是一定的,代入统计表的数据,即可完成空格里的内容。
【详解】
同一时间,同一地点,竹竿的高和竿影的长成正比例。
4÷1.25=3.2(米)
7÷1.25=5.6(米)
竹竿的高度/m 1 2 4 6 7
影长/m 0.8 1.6 3.2 4.8 5.6
3.正
【分析】相对应的两个量x和y的比值一定,即=k(定值),那么这两个量叫做成正比例的量,它们的关系叫做正比例关系;据此解答。
【详解】根据正比例的意义可得:如果a∶b的值一定(a、b均不为0),那么a和b成正比例。
故答案为:正
【点睛】本题主要考查正比例的意义,解题时要明确相关联的两种量若比值一定,就成正比例。
4. 哥哥 正
【分析】(1)哥哥和弟弟骑得距离一样,只要比较谁花的时间少,就知道谁骑车的速度快。
(2)判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【详解】(1)观察图可知:哥哥和弟弟两人都行了12千米,哥哥用的时间少,所以哥哥骑车的速度快;
(2)因为路程∶时间=速度(一定),是比值一定,所以哥哥骑行的路程和时间成正比例。
【点睛】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
5. 页数 天数 天数 20 正
【分析】(1)上表中,表格中是页数和天数两种相关联的量,看的页数的多少是随着天数的变化而变化的;
(2)看的页数与天数这两种量中相对应的两个数的比值,即页数÷天数;
(3)因为页数÷天数=每天看的页数,所以每天看的页数,即比值一定,所以看的页数与看的天数成正比例,据此解答。
【详解】(1)表格中的页数和天数是两种相关联的量,看的页数的多少是随着天数的变化而变化的;
(2)看的页数与看的天数这两种量中相对应的两个数的比值是20∶1=40∶2=20;
(3)因为每天看的页数一定,所以看的页数与看的天数成正比例关系。
【点睛】本题重在考查比的意义、求比值以及正比例、反比例关系的判断方法。
6. 正
【分析】根据比例的基本性质:内项积=外项积,即m∶n=3∶7,由于3∶7=3÷7=,所以m和n的比值一定,根据正比例的判定方法:当两个相关联的量比值一定,则成正比例关系,据此即可填空。
【详解】由于m∶n=3∶7
则m∶n=3÷7=,即=
如果7m=3n(m,n均不为0),那么m与n成正比例,=。
【点睛】本题主要考查比例的基本性质以及正比例的意义,熟练掌握正比例的意义是解题的关键。
7.底面积
【分析】判断体积和底面积、半径、周长是否成比例,就看这两种量是否是对应的乘积(商)一定,如果是乘积(商)一定,就成反(正)比例,如果不是乘积(商)一定或乘积(商)不一定,就不成比例。
【详解】因为:圆柱的体积÷底面积=高(一定)也就是圆柱的体积与底面积的商一定,符合正比例的意义,所以圆柱的体积与底面积成正比例
【点睛】此题考查用正反比例的意义辨识成正比例的量与成反比例的量。
8.A
【分析】两种相关联的量中相对应的两个数的商一定,就成正比例关系,正比例的图象是一条过原点的直线。
【详解】由分析可知;正比例图象是一条直线。
故答案为:A
【点睛】本题考查了对正比例图象的认识,属于基础知识。
9.C
【分析】根据(一定),x和y成正比例关系,进行选择。
【详解】A. (一定),x和y不成比例关系;
B. (一定),x和y成反比例关系;
C. (一定),x和y成正比例关系。
故答案为:C
【点睛】本题考查了辨识正比例的量,商一定是正比例关系,积一定是反比例关系。
10.A
【解析】略
11.C
【分析】根据“两个相关联的量,一个量变化,另一个量也随着变化,如果相对应的两个量x和y的比值一定,即=k(定值),那么这两个量叫做成正比例的量,它们的关系叫做正比例关系。”解答即可。
【详解】A、因为圆的面积÷半径=圆周率×半径(不一定),所以圆的面积和半径不成正比例,不符合题意;
B、因为圆的面积÷直径=圆周率×半径÷2(不一定),所以圆的面积和直径不成正比例,不符合题意;
C、因为圆的面积÷半径的平方=圆周率(一定),所以圆的面积和半径的平方成正比例,符合题意;
故答案为:C
【点睛】本题主要考查正比例关系的辨识,牢记圆的面积公式及正比例的意义是解题的关键。
12.A
【详解】略
13.A
【分析】根据数量关系判断出x和y的商一定还是乘积一定,如果商一定就成正比例,如果乘积一定就成反比例,否则不成比例。
【详解】因为3x=4y,所以x÷y=,x和y的商一定,二者成正比例。
故答案为:A
【点睛】本题考查正反比例的辨别,掌握正反比例的定义就能解决问题。
14.B
【详解】略
15.√
【详解】当圆柱的高一定时,即圆柱的底面周长和侧面积的商一定,所以底面周长和侧面积成正比例关系。
所以原题说法正确。
16.√
【分析】根据数量关系判断运货总重量与运的次数的商一定还是积一定,如果商一定就成正比例,如果积一定就成反比例,否则不成比例.
【详解】货物总重量÷运货的次数=一辆车的载重量,载重量一定,货物总重量与运货的次数的商一定,二者成正比例,原题说法正确.
故答案为正确
17.√
【详解】图上距离∶实际距离=比例尺,图上距离和实际距离的比值一定,二者成正比例。
故答案为:√
18.×
【分析】判断两个相关联的量之间成不成正比例,就看这两个量对应的数的比值是否一定。如果比值一定,就成正比例。据此即可解答。
【详解】因为出租车车票的价格=起步价+超过起步价的公里数×超过起步价公里数每行1千米所需要的钱数。所以所行的路程和所需费用不成正比例。
故答案为:×
【点睛】本题考查学生对成正比例的量知识的掌握。
19.(1)1.5;3;4.5;7.5
画图如下:
(2)单价没变,数量和总价成正比例。
(3)需要12元钱。
【分析】(1)根据总价÷数量=单价,求出单价,再根据单价×数量=总价,求出各自对应的总价;最后描点连线即可;
(2)根据总价、数量、单价之间的关系解答即可;
(3)根据根据总价÷数量=单价,求出单价,再根据单价×数量=总价,即可求出对应的总价。
【详解】(1)6÷4=1.5(元)
1.5×1=1.5(元)
1.5×2=3(元)
1.5×3=4.5(元)
1.5×5=7.5(元)
填表、画图如下:
数量/本 0 1 2 3 4 5 6 …
总价/元 0 1.5 3 4.5 6 7.5 9 …
(2)总价÷数量=单价(比值一定)即单价没变,所以数量和总价成正比例。
(3)6÷4×8
=1.5×8
=12(元)
答:买8本笔记本,需要12元。
【点睛】本题是一道基础题,主要考查单价、数量、总价的关系及正比例的意义。
20.33厘米
【分析】根据教学楼的实际高度与模型高度的比值是一定,即两种量成正比例;13.2米=1320厘米;设模型的高度是x厘米,列比例:40∶1=1320∶x,解比例,即可解答。
【详解】13.2米=1320厘米
解:设模型的高度是x厘米。
40∶1=1320∶x
40x=1×1320
x=1320÷40
x=33
答:模型的高度是33厘米。
【点睛】本题主要考查对正比例的意义的运用:两种相关联的量,一种量变化,另一种量也随着变化,但两种量的相对应的比值一定,这两种量成正比例;注意单位名数的统一。
21.(1)800千米
(2)7.5时
【分析】(1)根据图示可知,这辆车速度不变,路程乙时间成正比例,所以1小时行80千米,10小时行80×10千米;
(2)根据题意利用公式:时间=路程÷速度进行解答。
【详解】(1)80×10=800(千米)
答:10时行了800千米。
(2)600÷80=7.5(小时)
答:行驶600千米,需要7.5时。
【点睛】本题主要考查单式折线统计图,关键根据统计图找对解决问题的条件,利用路程、速度和时间之间的关系做题。
22.(1)正
(2)如图:
在同一条直线上
(3)(4,320)
(4)对
【分析】(1)两个相关联的量,乘积一定成反比例,比值一定成正比例,否则不成比例,据此分析即可;
(2)由图可知横轴表示时间,竖轴表示路程,根据表格数据描点、连线,观察即可;
(3)A点所对应的时间是4时,根据时间及比值,即可求出路程;
(4)求出640与8的比值,与其他比值相同则在这条直线上,据此解答即可。
【详解】(1)80∶1=80
160∶2=80
240∶3=80
80=80=80
则汽车行驶的时间和路程成正比例。
(2)如图:
我发现所描的点在同一条直线上。
(3)4×80=320(千米)
则点A是直线上的一点,这一点表示(4,320)。
(4)640∶8=80
则点(8,640)也在这条直线上,我认为他说得对。
【点睛】本题考查正比例的判断,解题的关键是明确:比值一定的两个量是成正比例关系的量,对应的各点都在同一条直线上。
答案第1页,共2页
答案第1页,共2页
