7.2.1三角函数的定义课件(共14张PPT)-2023-2024学年高一下学期数学人教B版(2019)必修第三册
文档属性
| 名称 | 7.2.1三角函数的定义课件(共14张PPT)-2023-2024学年高一下学期数学人教B版(2019)必修第三册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-06 00:00:00 | ||
图片预览





文档简介
(共14张PPT)
7.2 任意角的三角函数
7.2.1 三角函数的定义
新授课
1. 理解任意角三角函数的定义并能计算简单的三角函数的值;
2. 了解任意角三角数(正弦、余弦、正切)的定义域,并能判断三角函数在各象限的符号.
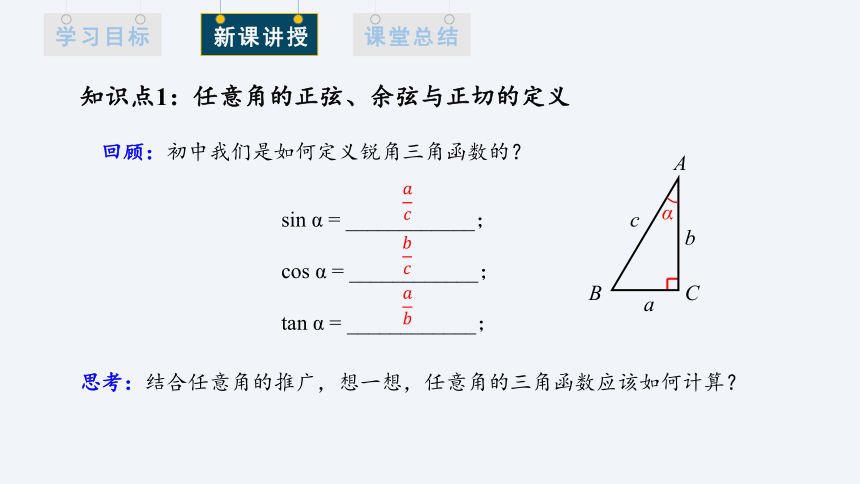
回顾:初中我们是如何定义锐角三角函数的?
知识点1:任意角的正弦、余弦与正切的定义
思考:结合任意角的推广,想一想,任意角的三角函数应该如何计算?
sin α = ____________;
cos α = ____________;
tan α = ____________;
A
B
C
α
a
b
c
问题 1:当 α 是一个锐角时,试着通过 α 终边上的点的坐标来定义它的正弦、余弦、正切.
x
y
O
α
P (x,y)
M
如图所示,在 α 终边上任取一个不同于坐标原点的点 P (x,y),作 PM 垂直 Ox 于点 M,
记 r = ,则△OMP 是一个直角三角形,且OM = x,PM = y,OP = r,由此可知:
sin α = = ,cos α = = ,tan α = = .
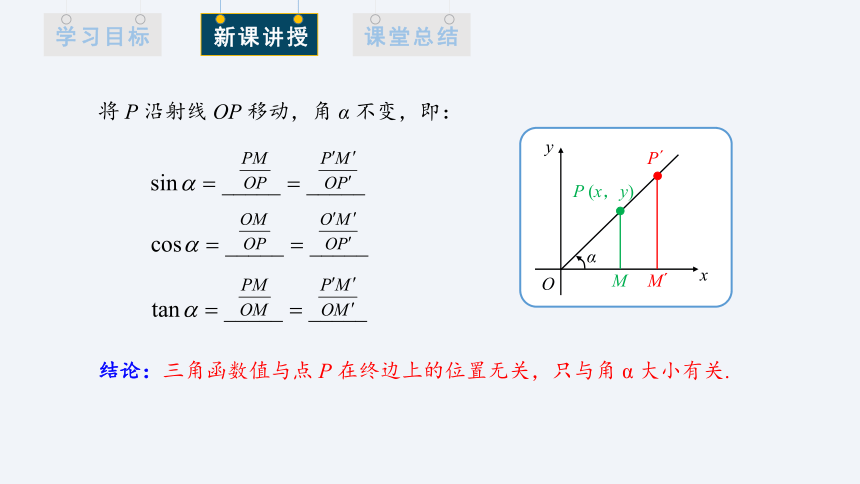
思考:点 P 的位置不同,是否会影响 α 的三角函数值呢?
x
y
O
α
P (x,y)
M
P
M
将 P 沿射线 OP 移动,角 α 不变,即:
结论:三角函数值与点 P 在终边上的位置无关,只与角 α 大小有关.
问题 2:如何定义任意角 α 的正弦、余弦、正切.
如图所示,对于任意角 α,设点 P (x,y) 是 α 终边上异于原点的任意一点,r = ,则有:
当角 α 终边不在 y 轴上时,有:
由上可知,对于每一个角 α ,都有唯一确定的正弦、余弦与之对应;
当 α ≠ + kπ ( k∈Z ) 时,有唯一的正切与之对应;
角的正弦、余弦与正切,都称为的三角函数.
sin α = ,cos α =
tan α = (x ≠ 0).
例 1:已知角 α 的终边经过点 P (2,-3),求 sin α,cos α,tan α.
解:设 x = 2,y = -3,则 r = = ;
所以 sin α = =,cos α = = = ,tan α = .
典例剖析
例 2:求下列各角的正弦、余弦和正切.
(1)0; (2)π; (3).
解:(1)角 0 的终边在 x 轴的正半轴上,在 x 的正半轴上取点(1,0),
所以 r = = 1,因此 sin 0 = = 0,cos 0 = = 1,tan 0 = = 0;
(2)角 π 的终边在 x 轴的负半轴上,在 x 的负半轴上取点(–1,0),
所以 r = = 1,因此 sin π = = 0,cos π = = –1,tan 0 = = 0;
(3)角 的终边在 y 轴的负半轴上,在 y 的正半轴上取点(0,–1),
所以 r = = 1,因此 sin = –1,cos = 0,tan 不存在.
例 3:求 的正弦、余弦和正切.
解:如图所示,在 的终边上取点 P,使得 OP = 2.
作 PM⊥Ox ,则在 Rt△OMP 中,∠POM = π – = ,
因此 MP = 1,OM = ,从而可知 P 的坐标为(-,1),
因此 sin = ,cos = – ,tan = – .
x
y
O
P
M
知识点 2:正弦、余弦与正切在各象限的符号
问题 3 :根据任意角的三角函数定义,完成下列填空:
思考:结合上述定义,说一说,三角函数在坐标轴各象限中的符号?
三角函数 定义域
sin α
cos α
tan α
R
R
{ x | x ≠ + kπ (k∈Z) }
问题 4 :如图,将三种三角函数的值在各象限的符号填入相应位置的括号中,并说出填写的依据.
x
y
O
sin α
( )
+
( )
( )
x
y
O
cos α
( )
( )
( )
( )
x
y
O
tan α
( )
( )
( )
( )
+
–
–
+
–
+
+
+
–
–
–
例 3:确定下列各值的符号:
(1)cos 260 ; (2)sin(- ); (3)tan(- 672 20′); (4)tan .
典例剖析
解:(1)因为 260 是第三象限角,所以 cos 260 < 0;
(2)因为 - 是第四象限角,所以 sin(- ) < 0;
(3)由 - 672 20′ = 47 40′ + (-2)×360 ,可知 – 672 20′ 是第一象限角,
所以 tan(- 672 20′) > 0;
(4)由 = + 2π,可知 是第三象限角,所以 tan > 0.
例 5:设 sin θ < 0 且 tan θ > 0,确定 θ 是第几象限角.
解:因为 sin θ < 0,所以 θ 可能是第三、四象限的角;
又 tan θ > 0,θ 可能是第一、三象限的角;
综上所述,θ 是第三象限的角.
根据今天所学,回答下列问题:
(1)三角函数的定义是什么
(2)在三角函数中,任意角 α 分别需要满足怎样的条件?
(3)在三角函数中,角的终边与三角函数的符号有什么关系?
7.2 任意角的三角函数
7.2.1 三角函数的定义
新授课
1. 理解任意角三角函数的定义并能计算简单的三角函数的值;
2. 了解任意角三角数(正弦、余弦、正切)的定义域,并能判断三角函数在各象限的符号.
回顾:初中我们是如何定义锐角三角函数的?
知识点1:任意角的正弦、余弦与正切的定义
思考:结合任意角的推广,想一想,任意角的三角函数应该如何计算?
sin α = ____________;
cos α = ____________;
tan α = ____________;
A
B
C
α
a
b
c
问题 1:当 α 是一个锐角时,试着通过 α 终边上的点的坐标来定义它的正弦、余弦、正切.
x
y
O
α
P (x,y)
M
如图所示,在 α 终边上任取一个不同于坐标原点的点 P (x,y),作 PM 垂直 Ox 于点 M,
记 r = ,则△OMP 是一个直角三角形,且OM = x,PM = y,OP = r,由此可知:
sin α = = ,cos α = = ,tan α = = .
思考:点 P 的位置不同,是否会影响 α 的三角函数值呢?
x
y
O
α
P (x,y)
M
P
M
将 P 沿射线 OP 移动,角 α 不变,即:
结论:三角函数值与点 P 在终边上的位置无关,只与角 α 大小有关.
问题 2:如何定义任意角 α 的正弦、余弦、正切.
如图所示,对于任意角 α,设点 P (x,y) 是 α 终边上异于原点的任意一点,r = ,则有:
当角 α 终边不在 y 轴上时,有:
由上可知,对于每一个角 α ,都有唯一确定的正弦、余弦与之对应;
当 α ≠ + kπ ( k∈Z ) 时,有唯一的正切与之对应;
角的正弦、余弦与正切,都称为的三角函数.
sin α = ,cos α =
tan α = (x ≠ 0).
例 1:已知角 α 的终边经过点 P (2,-3),求 sin α,cos α,tan α.
解:设 x = 2,y = -3,则 r = = ;
所以 sin α = =,cos α = = = ,tan α = .
典例剖析
例 2:求下列各角的正弦、余弦和正切.
(1)0; (2)π; (3).
解:(1)角 0 的终边在 x 轴的正半轴上,在 x 的正半轴上取点(1,0),
所以 r = = 1,因此 sin 0 = = 0,cos 0 = = 1,tan 0 = = 0;
(2)角 π 的终边在 x 轴的负半轴上,在 x 的负半轴上取点(–1,0),
所以 r = = 1,因此 sin π = = 0,cos π = = –1,tan 0 = = 0;
(3)角 的终边在 y 轴的负半轴上,在 y 的正半轴上取点(0,–1),
所以 r = = 1,因此 sin = –1,cos = 0,tan 不存在.
例 3:求 的正弦、余弦和正切.
解:如图所示,在 的终边上取点 P,使得 OP = 2.
作 PM⊥Ox ,则在 Rt△OMP 中,∠POM = π – = ,
因此 MP = 1,OM = ,从而可知 P 的坐标为(-,1),
因此 sin = ,cos = – ,tan = – .
x
y
O
P
M
知识点 2:正弦、余弦与正切在各象限的符号
问题 3 :根据任意角的三角函数定义,完成下列填空:
思考:结合上述定义,说一说,三角函数在坐标轴各象限中的符号?
三角函数 定义域
sin α
cos α
tan α
R
R
{ x | x ≠ + kπ (k∈Z) }
问题 4 :如图,将三种三角函数的值在各象限的符号填入相应位置的括号中,并说出填写的依据.
x
y
O
sin α
( )
+
( )
( )
x
y
O
cos α
( )
( )
( )
( )
x
y
O
tan α
( )
( )
( )
( )
+
–
–
+
–
+
+
+
–
–
–
例 3:确定下列各值的符号:
(1)cos 260 ; (2)sin(- ); (3)tan(- 672 20′); (4)tan .
典例剖析
解:(1)因为 260 是第三象限角,所以 cos 260 < 0;
(2)因为 - 是第四象限角,所以 sin(- ) < 0;
(3)由 - 672 20′ = 47 40′ + (-2)×360 ,可知 – 672 20′ 是第一象限角,
所以 tan(- 672 20′) > 0;
(4)由 = + 2π,可知 是第三象限角,所以 tan > 0.
例 5:设 sin θ < 0 且 tan θ > 0,确定 θ 是第几象限角.
解:因为 sin θ < 0,所以 θ 可能是第三、四象限的角;
又 tan θ > 0,θ 可能是第一、三象限的角;
综上所述,θ 是第三象限的角.
根据今天所学,回答下列问题:
(1)三角函数的定义是什么
(2)在三角函数中,任意角 α 分别需要满足怎样的条件?
(3)在三角函数中,角的终边与三角函数的符号有什么关系?
