7.3.5 已知三角函数值求角课件(共13张PPT)-2023-2024学年高一下学期数学人教B版(2019)必修第三册
文档属性
| 名称 | 7.3.5 已知三角函数值求角课件(共13张PPT)-2023-2024学年高一下学期数学人教B版(2019)必修第三册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-06 12:22:41 | ||
图片预览





文档简介
(共13张PPT)
7.3 三角函数的性质与图像
7.3.5 已知三角函数值求角
新授课
1. 掌握利用三角函数线求角的方法,会由已知的三角函数值求角,并会用符号 arcsin x,arccos x,arctan x 表示角;
2. 熟记一些比较常见的三角函数值及其在区间[– 2π,2π]上对应的角.
问题 1:若已知 sin x = ,试求出满足条件的角 x ?
知识点 1 :利用三角函数线求角
O
P1
1
N
P
M
由 sin x = > 0 可知,角 x 对应的正弦线方向朝上,
且长度为 .
做出如图示意图,由图可知角 x 的终边可能是 OP,
也可能是 OP1;
又因为 sin = sin = ,所以 x = + 2kπ 或 x = + 2kπ,k∈Z.
问题 2:若已知 sin x ≥ ,试求出角 x 的取值范围?
O
P1
1
N
P
M
由图可知,若 x 的终边在∠POP1中,则一定有 sin x ≥ ,
因此 x 的取值范围是 + 2kπ ≤ x ≤ + 2kπ,k∈Z.
思考:若不借助三角函数线,你还有其它的方法解答上述问题吗?
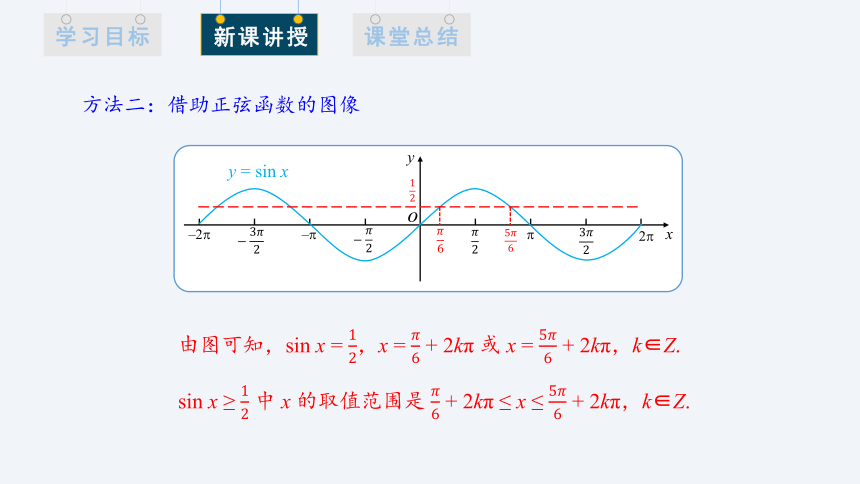
方法二:借助正弦函数的图像
由图可知,sin x = ,x = + 2kπ 或 x = + 2kπ,k∈Z.
sin x ≥ 中 x 的取值范围是 + 2kπ ≤ x ≤ + 2kπ,k∈Z.
x
y
o
–
2
–2
y = sin x
例 1:已知 cos (2x + ) = – ,求 x .
典例剖析
解:由cos (2x+) = – < 0可知,角2x + 对应的余弦线方向朝左,且长度为;
做示意图,由图可知角2x + 的终边可能是OP,也可能是OP1;
又因为 cos = cos = – ,
所以 2x + = + 2kπ 或 2x + = + 2kπ,k∈Z;
即 x = + kπ 或 x = + kπ,k∈Z.
O
P1
–1
M
P
练一练
1. 已知不等式 cos (2x + ) < – ,求 x 的解集.
由图可知,当 cos (2x + ) < – 时,
+ 2kπ < 2x + < + 2kπ,
所以不等式的解集为 ( + kπ, + kπ) k∈Z.
O
P1
–1
M
P
解:由 tan x = – 1 < 0 可知,角 x 对应的正切线的方向朝下,且长度为 1;
作如图示意图,由图可知,角 x 的终边可能是OT,也可能是OT1;
又因为 tan () = tan (π ) = – 1,
所以 x = + kπ,k∈Z.
又由3π < + kπ < 5π,k∈Z 可知 k = 4 或 k = 5,
因此 x = 或 x = ;
例 2:已知 tan x = – 1,x∈(3π,5π),求 x.
典例剖析
O
T1
1
A
T
练一练
2. 已知不等式 tan x > – 1,求 x 的解集.
由图可知,tan x > – 1 时, + kπ < x < + kπ,
所以不等式 tan x > – 1 的解集为
( + kπ, + kπ) k∈Z.
O
T1
1
A
T
知识点 2 :反三角函数
问题 2:若已知 sin x = ,且 x∈[,],求 x 的值.
任意给定一个 y∈[-1,1],满足 sin x = y 的 x 在区间 [,] 内只有一个,利用计算器或计算机软件可以方便地求出这个 x 的值;
如图所示,此时要在区间 [,] 内求满足
sin x = 的 x 的值,只要输入 sin-10.5 即可.
在数学中,任意给定一个 y∈[-1,1],当 sin x = y 且 x∈[,] 时,通常记作 x = arcsin y (反正弦函数);
类似地,在区间 [0,π] 内,满足 cos x = y ( y∈[-1,1] ) 的 x 只有一个,这个 x 记作 arccos y,即 x = arccos y (反余弦函数);
在区间 [,] 内,满足 tan x = y ( y∈R ) 的 x 只有一个,这个 x 记作 arctan y,即 x = arctan y (反正切函数).
概念讲解
例 3:计算下列反三角函数的值.
(1)arcsin ; (2)arccos 0; (3)arctan 1.
典例剖析
解:(1)arcsin = ; (2)arccos 0 = ; (3)arctan 1 = .
根据今天所学,回答下列问题:
(1)简述由已知的三角函数值求角的方法?
(2)说一说三角函数与反三角函数之间的关系?
7.3 三角函数的性质与图像
7.3.5 已知三角函数值求角
新授课
1. 掌握利用三角函数线求角的方法,会由已知的三角函数值求角,并会用符号 arcsin x,arccos x,arctan x 表示角;
2. 熟记一些比较常见的三角函数值及其在区间[– 2π,2π]上对应的角.
问题 1:若已知 sin x = ,试求出满足条件的角 x ?
知识点 1 :利用三角函数线求角
O
P1
1
N
P
M
由 sin x = > 0 可知,角 x 对应的正弦线方向朝上,
且长度为 .
做出如图示意图,由图可知角 x 的终边可能是 OP,
也可能是 OP1;
又因为 sin = sin = ,所以 x = + 2kπ 或 x = + 2kπ,k∈Z.
问题 2:若已知 sin x ≥ ,试求出角 x 的取值范围?
O
P1
1
N
P
M
由图可知,若 x 的终边在∠POP1中,则一定有 sin x ≥ ,
因此 x 的取值范围是 + 2kπ ≤ x ≤ + 2kπ,k∈Z.
思考:若不借助三角函数线,你还有其它的方法解答上述问题吗?
方法二:借助正弦函数的图像
由图可知,sin x = ,x = + 2kπ 或 x = + 2kπ,k∈Z.
sin x ≥ 中 x 的取值范围是 + 2kπ ≤ x ≤ + 2kπ,k∈Z.
x
y
o
–
2
–2
y = sin x
例 1:已知 cos (2x + ) = – ,求 x .
典例剖析
解:由cos (2x+) = – < 0可知,角2x + 对应的余弦线方向朝左,且长度为;
做示意图,由图可知角2x + 的终边可能是OP,也可能是OP1;
又因为 cos = cos = – ,
所以 2x + = + 2kπ 或 2x + = + 2kπ,k∈Z;
即 x = + kπ 或 x = + kπ,k∈Z.
O
P1
–1
M
P
练一练
1. 已知不等式 cos (2x + ) < – ,求 x 的解集.
由图可知,当 cos (2x + ) < – 时,
+ 2kπ < 2x + < + 2kπ,
所以不等式的解集为 ( + kπ, + kπ) k∈Z.
O
P1
–1
M
P
解:由 tan x = – 1 < 0 可知,角 x 对应的正切线的方向朝下,且长度为 1;
作如图示意图,由图可知,角 x 的终边可能是OT,也可能是OT1;
又因为 tan () = tan (π ) = – 1,
所以 x = + kπ,k∈Z.
又由3π < + kπ < 5π,k∈Z 可知 k = 4 或 k = 5,
因此 x = 或 x = ;
例 2:已知 tan x = – 1,x∈(3π,5π),求 x.
典例剖析
O
T1
1
A
T
练一练
2. 已知不等式 tan x > – 1,求 x 的解集.
由图可知,tan x > – 1 时, + kπ < x < + kπ,
所以不等式 tan x > – 1 的解集为
( + kπ, + kπ) k∈Z.
O
T1
1
A
T
知识点 2 :反三角函数
问题 2:若已知 sin x = ,且 x∈[,],求 x 的值.
任意给定一个 y∈[-1,1],满足 sin x = y 的 x 在区间 [,] 内只有一个,利用计算器或计算机软件可以方便地求出这个 x 的值;
如图所示,此时要在区间 [,] 内求满足
sin x = 的 x 的值,只要输入 sin-10.5 即可.
在数学中,任意给定一个 y∈[-1,1],当 sin x = y 且 x∈[,] 时,通常记作 x = arcsin y (反正弦函数);
类似地,在区间 [0,π] 内,满足 cos x = y ( y∈[-1,1] ) 的 x 只有一个,这个 x 记作 arccos y,即 x = arccos y (反余弦函数);
在区间 [,] 内,满足 tan x = y ( y∈R ) 的 x 只有一个,这个 x 记作 arctan y,即 x = arctan y (反正切函数).
概念讲解
例 3:计算下列反三角函数的值.
(1)arcsin ; (2)arccos 0; (3)arctan 1.
典例剖析
解:(1)arcsin = ; (2)arccos 0 = ; (3)arctan 1 = .
根据今天所学,回答下列问题:
(1)简述由已知的三角函数值求角的方法?
(2)说一说三角函数与反三角函数之间的关系?
