1.4.2 单位圆与正弦函数、余弦函数的基本性质 课件(共19张PPT)-2023-2024学年高一下学期数学北师版(2019)必修第二册
文档属性
| 名称 | 1.4.2 单位圆与正弦函数、余弦函数的基本性质 课件(共19张PPT)-2023-2024学年高一下学期数学北师版(2019)必修第二册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-06 00:00:00 | ||
图片预览






文档简介
(共19张PPT)
第一章 三角函数
北师大版(2019)高中数学必修第二册
4.2单位圆与正弦函数、
余弦函数的基本性质
目录
01 ·复习导入
02 ·新知概念
03 ·归纳总结
04 ·典例剖析
复习导入
设 α 是一个任意角, α ∈R,它的终边 OP 与单位圆交于点 P(x, y), 把点 P 的纵坐标 y 定义为角 α 的正弦函数,即 y = sin α; 把点 P 的横坐标 x 定义为角 α 的余弦函数,即x = cos α.
O
α
P
正弦函数、余弦函数和正切函数的基本性质
新知概念
1.写出任意角的正弦函数,余弦函数的解析
式?对应的定义域是什么?
问题:借助单位圆和正弦函数的定义,如图,你能探究正弦函数y=sin的基本性质吗?
O
α
P
M
A(1,0)
正弦函数:;
余弦函数:
正弦函数余弦函数的定义域均为:实数集
新知概念
2.最大(小)值、值域
正弦函数、余弦函数和正切函数的基本性质
(1)当时,正弦函数取得最大值,最大值为
当时,正弦函数取得最小值,最小值为
正弦函数的值域为
(2)当时,余弦函数取得最大值,最大值为
当时,正弦函数取得最小值,最小值为
余弦函数的值域为
时,,.
P
A(1,0)
新知概念
正弦函数、余弦函数和正切函数的基本性质
3.周期性
正弦函数和余弦函数主要从终边相同的角去处理,
结合定义得:
(1)终边相同的角正弦函数值相等,
即对任意
正弦函数的最小正周期为.
(2)终边相同的角余弦函数值相等,
即对任意
余弦函数的最小正周期为.
正弦函数和余弦函数均是周期函数,
对任何且,均是它们的周期,最小正周期为.
新知概念
正弦函数、余弦函数和正切函数的基本性质
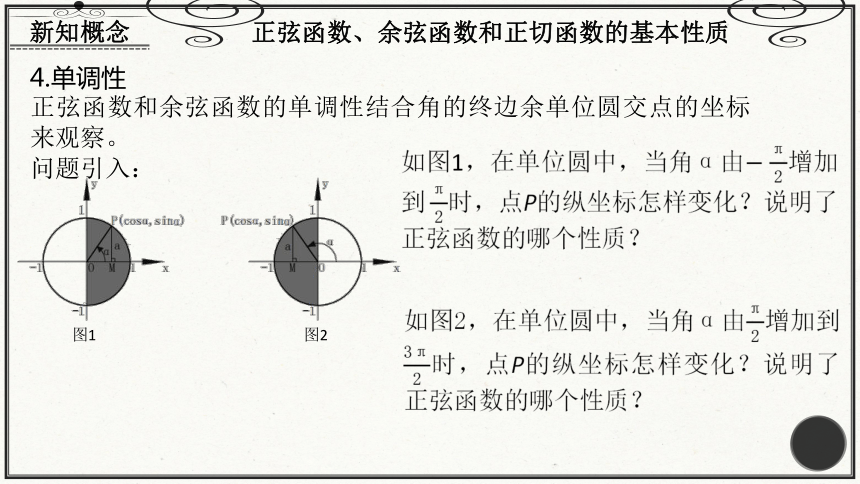
4.单调性
正弦函数和余弦函数的单调性结合角的终边余单位圆交点的坐标来观察。
问题引入:
图1
图2
如图1,在单位圆中,当角由增加时,点P的纵坐标怎样变化?说明了正弦函数的哪个性质?
如图2,在单位圆中,当角由增加到时,点P的纵坐标怎样变化?说明了正弦函数的哪个性质?
新知概念
正弦函数、余弦函数和正切函数的基本性质
4.单调性
正弦函数和余弦函数的单调性结合角的终边余单位圆交点的坐标来观察。
问题引入:
图3
图4
如图3,在单位圆中,当角由增加到时,点P的纵坐标怎样变化?说明了正弦函数的哪个性质?
如图4,在单位圆中,当角由增加到时,点P的纵坐标怎样变化?说明了正弦函数的哪个性质?
新知概念
正弦函数、余弦函数和正切函数的基本性质
正弦函数的单调性:
正弦函数在区间上单调递增,在区间上单调递减.
由正弦函数的周期性可知,
对任意的,正弦函数在区间上单调递增,
在区间上单调递减.
余弦函数的单调性:
余弦函数在区间上单调递减,在区间上单调递增.
由余弦函数的周期性可知,
对任意的,余弦函数在区间上单调递减,
在区间上单调递增.
归纳总结
新知概念
正弦函数值和余弦函数值的符号
通过常见特殊角的三角函数值,你还能总结出什么规律?
y=sinα
规律:
正弦函数值对于第一、二象限角是正的,
对于第三四象限角是负的.
同理,余弦函数值在第一四象限角是正的,
在第二、三象限角是负的.
(一均正、二正弦、三均负、四余弦)
归纳总结
正弦函数、余弦函数和正切函数的基本性质
归纳总结
正弦函数、余弦函数和正切函数的基本性质
2π
2π
典例剖析
正弦函数、余弦函数和正切函数的基本性质
例1 借助单位圆,讨论函数v=sin α在给定区间上的单调性.
解:(1)函数v=sin α在区间 上单调递增;
(2) 函数v=sin α在区间 上单调递增,
在区间 上单调递减.
典例剖析
正弦函数、余弦函数和正切函数的基本性质
例2 求函数在区间上的最大值和最小值,并写出取得最大值和最小值时自变量α的值.
解:如图
当时,函数取得最大值,
最大值为,
当时,函数取得最小值,
最小值为.
典例剖析
与正、余弦函数的定义域有关的问题
求函数 的定义域.
解:对数的真数大于零,二次根式的被开方数不小于零
由题意可知,定义域满足不等式组:
解得:
所以函数的定义域为:
题型1
典例剖析
正弦、余弦函数的周期问题
题型2 求下列各式的值.
典例剖析
正余弦函数单调性问题
题型3 设 , , ,则下列关系正确的是( )
A. B. C. D.
B
【答案】B
【分析】根据 的范围,分别求得 的范围,即可比较大小.
【详解】∵ ,
∴ ,∴ ;
典例剖析
正余弦函数值的符号
题型4 如果点P(2sin θ,sin θ·cos θ)位于第四象限,那么角θ所在象限
为( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
B
THANKS
第一章 三角函数
北师大版(2019)高中数学必修第二册
4.2单位圆与正弦函数、
余弦函数的基本性质
目录
01 ·复习导入
02 ·新知概念
03 ·归纳总结
04 ·典例剖析
复习导入
设 α 是一个任意角, α ∈R,它的终边 OP 与单位圆交于点 P(x, y), 把点 P 的纵坐标 y 定义为角 α 的正弦函数,即 y = sin α; 把点 P 的横坐标 x 定义为角 α 的余弦函数,即x = cos α.
O
α
P
正弦函数、余弦函数和正切函数的基本性质
新知概念
1.写出任意角的正弦函数,余弦函数的解析
式?对应的定义域是什么?
问题:借助单位圆和正弦函数的定义,如图,你能探究正弦函数y=sin的基本性质吗?
O
α
P
M
A(1,0)
正弦函数:;
余弦函数:
正弦函数余弦函数的定义域均为:实数集
新知概念
2.最大(小)值、值域
正弦函数、余弦函数和正切函数的基本性质
(1)当时,正弦函数取得最大值,最大值为
当时,正弦函数取得最小值,最小值为
正弦函数的值域为
(2)当时,余弦函数取得最大值,最大值为
当时,正弦函数取得最小值,最小值为
余弦函数的值域为
时,,.
P
A(1,0)
新知概念
正弦函数、余弦函数和正切函数的基本性质
3.周期性
正弦函数和余弦函数主要从终边相同的角去处理,
结合定义得:
(1)终边相同的角正弦函数值相等,
即对任意
正弦函数的最小正周期为.
(2)终边相同的角余弦函数值相等,
即对任意
余弦函数的最小正周期为.
正弦函数和余弦函数均是周期函数,
对任何且,均是它们的周期,最小正周期为.
新知概念
正弦函数、余弦函数和正切函数的基本性质
4.单调性
正弦函数和余弦函数的单调性结合角的终边余单位圆交点的坐标来观察。
问题引入:
图1
图2
如图1,在单位圆中,当角由增加时,点P的纵坐标怎样变化?说明了正弦函数的哪个性质?
如图2,在单位圆中,当角由增加到时,点P的纵坐标怎样变化?说明了正弦函数的哪个性质?
新知概念
正弦函数、余弦函数和正切函数的基本性质
4.单调性
正弦函数和余弦函数的单调性结合角的终边余单位圆交点的坐标来观察。
问题引入:
图3
图4
如图3,在单位圆中,当角由增加到时,点P的纵坐标怎样变化?说明了正弦函数的哪个性质?
如图4,在单位圆中,当角由增加到时,点P的纵坐标怎样变化?说明了正弦函数的哪个性质?
新知概念
正弦函数、余弦函数和正切函数的基本性质
正弦函数的单调性:
正弦函数在区间上单调递增,在区间上单调递减.
由正弦函数的周期性可知,
对任意的,正弦函数在区间上单调递增,
在区间上单调递减.
余弦函数的单调性:
余弦函数在区间上单调递减,在区间上单调递增.
由余弦函数的周期性可知,
对任意的,余弦函数在区间上单调递减,
在区间上单调递增.
归纳总结
新知概念
正弦函数值和余弦函数值的符号
通过常见特殊角的三角函数值,你还能总结出什么规律?
y=sinα
规律:
正弦函数值对于第一、二象限角是正的,
对于第三四象限角是负的.
同理,余弦函数值在第一四象限角是正的,
在第二、三象限角是负的.
(一均正、二正弦、三均负、四余弦)
归纳总结
正弦函数、余弦函数和正切函数的基本性质
归纳总结
正弦函数、余弦函数和正切函数的基本性质
2π
2π
典例剖析
正弦函数、余弦函数和正切函数的基本性质
例1 借助单位圆,讨论函数v=sin α在给定区间上的单调性.
解:(1)函数v=sin α在区间 上单调递增;
(2) 函数v=sin α在区间 上单调递增,
在区间 上单调递减.
典例剖析
正弦函数、余弦函数和正切函数的基本性质
例2 求函数在区间上的最大值和最小值,并写出取得最大值和最小值时自变量α的值.
解:如图
当时,函数取得最大值,
最大值为,
当时,函数取得最小值,
最小值为.
典例剖析
与正、余弦函数的定义域有关的问题
求函数 的定义域.
解:对数的真数大于零,二次根式的被开方数不小于零
由题意可知,定义域满足不等式组:
解得:
所以函数的定义域为:
题型1
典例剖析
正弦、余弦函数的周期问题
题型2 求下列各式的值.
典例剖析
正余弦函数单调性问题
题型3 设 , , ,则下列关系正确的是( )
A. B. C. D.
B
【答案】B
【分析】根据 的范围,分别求得 的范围,即可比较大小.
【详解】∵ ,
∴ ,∴ ;
典例剖析
正余弦函数值的符号
题型4 如果点P(2sin θ,sin θ·cos θ)位于第四象限,那么角θ所在象限
为( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
B
THANKS
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
