7.2离散型随机变量及其分布列课件(共21张PPT)-2023-2024学年高二下学期数学人教A版(2019)选择性必修第三册
文档属性
| 名称 | 7.2离散型随机变量及其分布列课件(共21张PPT)-2023-2024学年高二下学期数学人教A版(2019)选择性必修第三册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-06 00:00:00 | ||
图片预览








文档简介
(共21张PPT)
7.2
离散型随机变量及其分布列
人教A版(2019)选择性必修第三册
学习目标
1.通过实例,了解离散型随机变量的概念.
2.掌握离散型随机变量分布列的表示方法和性质.
3.掌握两点分布列有关知识及应用.
4.理解两个相关随机变量的分布列的关系.
5.核心素养:数学抽象、逻辑推理、数学运算.
一、复习导入
1、随机变量:如果在随机试验中确定一个对应关系,使得每个试验结果都用一个确定的数字表示,在这个对应关系下,数字随着试验结果的变化而变化,像这种随着试验结果变化而变化的变量称为随机变量.
随机变量常用字母,…等表示.
2、随机变量与函数的联系:随机变量和函数都是一种映射,试验结果的范围相当于函数的定义域,随机变量的取值范围相当于函数的值域.
随机变量与函数的区别:随机变量把试验结果映射为实数,函数把实数映射为实数.
二、新课讲授
问题1 什么是离散型随机变量?
对于随机变量可能取的值,如果可以一一列出,这样的随机变量叫做离散型随机变量.
练习 以下问题中的是离散型随机变量的是( )
①某座大桥一天经过的车辆数为;
②某无线寻呼一天内收到寻呼的次数为;
③一天之内的温度数为;
④某市年内的下雨次数为;
①②④
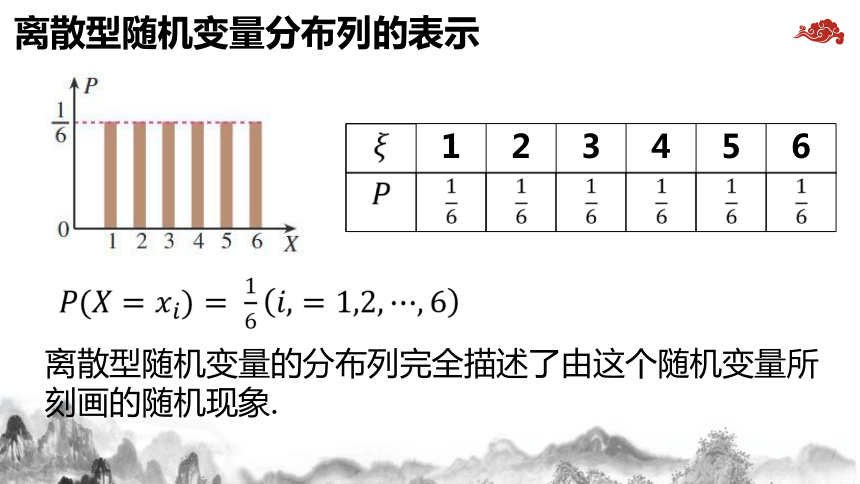
问题2 抛掷一枚质地均匀的骰子,所得的点数有哪些值? 取每个值的概率是多少?
解: 可能的取值为1,2,3,4,5,6.
, , ,
, , ,
1 2 3 4 5 6
的分布列
1、列出随机变量的所有取值;
2、求出的每一个取值的概率.
离散型随机变量的分布列
一般地,若离散型随机变量可能取的不同值为:
, ,…,
取的每一个 的概率 ,则称表格
…
…
为离散型随机变量的概率分布列,简称的分布列.有时为了表达简单,也用等式
来表示的分布列.
抛掷一枚骰子,所得的点数的分布列为:
1 2 3 4 5 6
问题3 分别求出{是偶数}和{<3}两个事件的概率?
解: + +
=++=
+ =
离散型随机变量分布列的表示
1 2 3 4 5 6
离散型随机变量的分布列完全描述了由这个随机变量所刻画的随机现象.
离散型随机变量分布列的两个性质
…
…
1、 ≥0,;
2、
问题4 一个口袋中有5只同样的小球,编号分别为1,2,3,3,4.若从中任取1只,以表示取出的球的号码,求的分布列.
解: 可能的取值为1,2,3,4.
, ,
, ,
的分布列为:
1 2 3 4
求离散型随机变量分布列的基本步骤:
1、列出随机变量的所有取值;
2、求出的每一个取值的概率;
3、列出表格.
古典概型:
(1)有限性:样本空间的样本点只有有限个。
(2)等可能性:每个样本点发生的可能性相等。
随机事件的概率其中表示事件包含的基本事件个数,即表示总的基本事件个,即.
问题5 投掷一枚图钉一次,若针尖朝上的概率为,设.
写出随机变量的分布列.
解: 可能的取值为0,1.
,
的分布列为:
0 1
两点分布列
两点分布:
两点分布即“伯努利分布”.在一次试验中,事件出现的概率为,事件不出现的概率为,若以记一次试验中出现的次数,则仅取0、1两个值. 的概率分布列
称服从两点分布(伯努利分布)
简记为:
问题6 盒中装有12个乒乓球,其中9个正品,3个次品,从盒中任取3个球,设这3个球中次品数是一个随机变量,求的分布列.
解:可能的取值为0,1,2,3.
的分布列为:
0 1 2 3
超几何分布列
超几何分布:
一般地,在含有件次品的件产品中,任取件,其中恰有件次品,则事件{= }发生的概率 , 其中且≤ , ≤ , ∈.称以下分布列
为超几何分布列.
三、巩固新知
例1 同时抛掷两枚质地均匀的骰子,向上的点数之和为,求随机变量的分布列.
分析: 可能的取值为2,3,4,5,6,7,8,9,10,11,12.
的分布列为:
2 3 4 5 6 7 8 9 10 11 12
例2 若随机变量的分布列如下表所示,则常数= .
-1 0 1 2 3
四、课堂小结
1、离散型随机变量分布列:两点分布列、超几何分布列
五、作业布置
课本P60: 第4题
课本P61: 第4题
2、求随机变量分布列的步骤
7.2
离散型随机变量及其分布列
人教A版(2019)选择性必修第三册
学习目标
1.通过实例,了解离散型随机变量的概念.
2.掌握离散型随机变量分布列的表示方法和性质.
3.掌握两点分布列有关知识及应用.
4.理解两个相关随机变量的分布列的关系.
5.核心素养:数学抽象、逻辑推理、数学运算.
一、复习导入
1、随机变量:如果在随机试验中确定一个对应关系,使得每个试验结果都用一个确定的数字表示,在这个对应关系下,数字随着试验结果的变化而变化,像这种随着试验结果变化而变化的变量称为随机变量.
随机变量常用字母,…等表示.
2、随机变量与函数的联系:随机变量和函数都是一种映射,试验结果的范围相当于函数的定义域,随机变量的取值范围相当于函数的值域.
随机变量与函数的区别:随机变量把试验结果映射为实数,函数把实数映射为实数.
二、新课讲授
问题1 什么是离散型随机变量?
对于随机变量可能取的值,如果可以一一列出,这样的随机变量叫做离散型随机变量.
练习 以下问题中的是离散型随机变量的是( )
①某座大桥一天经过的车辆数为;
②某无线寻呼一天内收到寻呼的次数为;
③一天之内的温度数为;
④某市年内的下雨次数为;
①②④
问题2 抛掷一枚质地均匀的骰子,所得的点数有哪些值? 取每个值的概率是多少?
解: 可能的取值为1,2,3,4,5,6.
, , ,
, , ,
1 2 3 4 5 6
的分布列
1、列出随机变量的所有取值;
2、求出的每一个取值的概率.
离散型随机变量的分布列
一般地,若离散型随机变量可能取的不同值为:
, ,…,
取的每一个 的概率 ,则称表格
…
…
为离散型随机变量的概率分布列,简称的分布列.有时为了表达简单,也用等式
来表示的分布列.
抛掷一枚骰子,所得的点数的分布列为:
1 2 3 4 5 6
问题3 分别求出{是偶数}和{<3}两个事件的概率?
解: + +
=++=
+ =
离散型随机变量分布列的表示
1 2 3 4 5 6
离散型随机变量的分布列完全描述了由这个随机变量所刻画的随机现象.
离散型随机变量分布列的两个性质
…
…
1、 ≥0,;
2、
问题4 一个口袋中有5只同样的小球,编号分别为1,2,3,3,4.若从中任取1只,以表示取出的球的号码,求的分布列.
解: 可能的取值为1,2,3,4.
, ,
, ,
的分布列为:
1 2 3 4
求离散型随机变量分布列的基本步骤:
1、列出随机变量的所有取值;
2、求出的每一个取值的概率;
3、列出表格.
古典概型:
(1)有限性:样本空间的样本点只有有限个。
(2)等可能性:每个样本点发生的可能性相等。
随机事件的概率其中表示事件包含的基本事件个数,即表示总的基本事件个,即.
问题5 投掷一枚图钉一次,若针尖朝上的概率为,设.
写出随机变量的分布列.
解: 可能的取值为0,1.
,
的分布列为:
0 1
两点分布列
两点分布:
两点分布即“伯努利分布”.在一次试验中,事件出现的概率为,事件不出现的概率为,若以记一次试验中出现的次数,则仅取0、1两个值. 的概率分布列
称服从两点分布(伯努利分布)
简记为:
问题6 盒中装有12个乒乓球,其中9个正品,3个次品,从盒中任取3个球,设这3个球中次品数是一个随机变量,求的分布列.
解:可能的取值为0,1,2,3.
的分布列为:
0 1 2 3
超几何分布列
超几何分布:
一般地,在含有件次品的件产品中,任取件,其中恰有件次品,则事件{= }发生的概率 , 其中且≤ , ≤ , ∈.称以下分布列
为超几何分布列.
三、巩固新知
例1 同时抛掷两枚质地均匀的骰子,向上的点数之和为,求随机变量的分布列.
分析: 可能的取值为2,3,4,5,6,7,8,9,10,11,12.
的分布列为:
2 3 4 5 6 7 8 9 10 11 12
例2 若随机变量的分布列如下表所示,则常数= .
-1 0 1 2 3
四、课堂小结
1、离散型随机变量分布列:两点分布列、超几何分布列
五、作业布置
课本P60: 第4题
课本P61: 第4题
2、求随机变量分布列的步骤
