北师大版七年级下册第二次月考测试卷(含答案)
文档属性
| 名称 | 北师大版七年级下册第二次月考测试卷(含答案) | 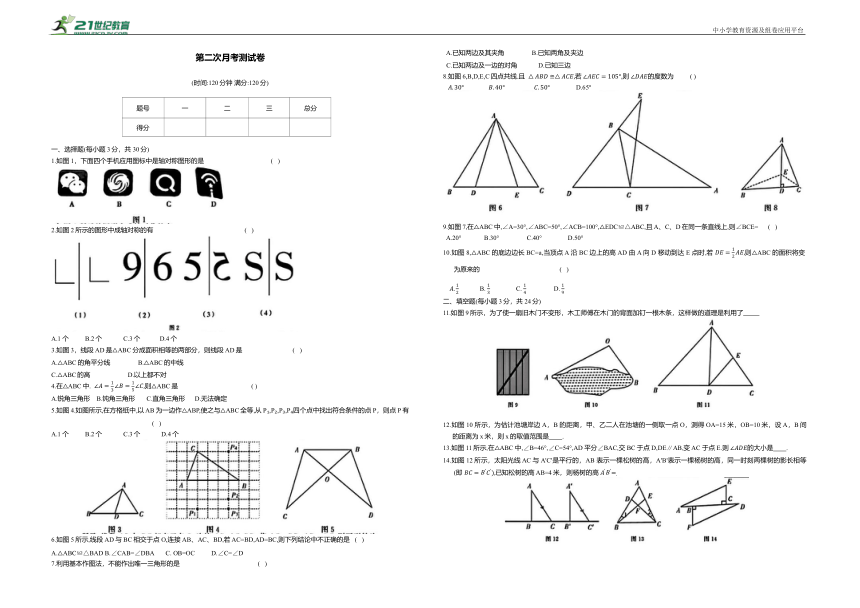 | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-06 16:14:55 | ||
图片预览

文档简介
第二次月考测试卷
(时间:120分钟 满分:120分)
题号 一 二 三 总分
得分
一、选择题(每小题3分,共30分)
1.如图1,下面四个手机应用图标中是轴对称图形的是 ( )
2.如图2所示的图形中成轴对称的有 ( )
A.1个 B.2个 C.3个 D.4个
3.如图3,线段AD是△ABC分成面积相等的两部分,则线段AD是 ( )
A.△ABC的角平分线 B.△ABC的中线
C.△ABC的高 D.以上都不对
4.在△ABC中. 则△ABC是 ( )
A.锐角三角形 B.钝角三角形 C.直角三角形 D.无法确定
5.如图4.如图所示,在方格纸中,以 AB为一边作△ABP,使之与△ABC全等,从P ,P ,P ,P 四个点中找出符合条件的点 P,则点 P有 ( )
A.1个 B.2个 C.3个 D.4个
6.如图5所示,线段AD与BC 相交于点O,连接AB、AC、BD,若 AC=BD,AD=BC,则下列结论中不正确的是 ( )
A.△ABC≌△BAD B.∠CAB=∠DBA C. OB=OC D.∠C=∠D
7.利用基本作图法,不能作出唯一三角形的是 ( )
A.已知两边及其夹角 B.已知两角及夹边
C.已知两边及一边的对角 D.已知三边
8.如图6,B,D,E,C四点共线.且 若 则 的度数为 ( )
D.65°
9.如图7,在△ABC中,∠A=30°,∠ABC=50°,∠ACB=100°,△EDC≌△ABC,且 A、C、D在同一条直线上,则∠BCE= ( )
A.20° B.30° C.40° D.50°
10.如图8,△ABC的底边边长BC=a,当顶点 A 沿 BC 边上的高AD 由A 向 D 移动到达 E 点时,若 则△ABC的面积将变为原来的 ( )
B. C. D.
二、填空题(每小题3分,共24分)
11.如图9所示,为了使一扇旧木门不变形,木工师傅在木门的背面加钉一根木条,这样做的道理是利用了
12.如图10 所示,为估计池塘岸边A,B 的距离,甲、乙二人在池塘的一侧取一点O,测得OA=15米,OB=10米,设A,B间的距离为x米,则x的取值范围是 .
13.如图11所示,在△ABC 中,∠B=46°,∠C=54°,AD平分∠BAC,交 BC于点 D,DE∥AB,变 AC 于点E.则 的大小是 .
14.如图12所示,太阳光线 AC与A'C'是平行的,AB 表示一棵松树的高,A'B'表示一棵杨树的高,同一时刻两棵树的影长相等(即 已知松树的高 AB=4米,则杨树的高
中小学教育资源及组卷应用平台
15.如图13所示,在△ABC中,已知∠1=∠2,BE=CD,AB=5,AE=2,则(
16.如图14 所示,A、B、C、D四点在一条直线上. 于C,FB⊥AD于B,若要使 则还需补充一个条件可以是 .(写出一种即可)
17.如图15 所示,是由我们熟悉的一些基本数学图形组成的,其中是轴对称图形的是 (填序号).
18.如图16所示,将△ABC三个角分别沿DE、HG、EF 翻折,三个顶点均落在点 O 处,则. 的度数为
三、解答题(共66分)
19.(10分)如图16 所示,在3×3的正方形网格中,有一个以格点为顶点的三角形(阴影部分),请你在图①②③中,分别画出一个与阴影三角形成轴对称且以格点为顶点的三角形,并将所画三角形涂上阴影.(注:所画的三个图不能重复)
20.(10分)如图17所示. P为AB的中点,点M 为射线AC上(不与点A 重合)的任意一点,连接MP,并使 P的延长线交射线 BD 于点 N. 试说明:
21.(10分)我们把两组邻边相等的四边形叫做“筝形”.如图18所示.四边形 ABCD 是一个筝形,其中 CB,AD=CD. 对角线AC,BD 相交于点O. 垂足分别是 E,F.试说明:(
22.(12分)如图19 所示,A,B 两个建筑物分别位于河的两岸,要测得它们之间的距离,可以从 B 出发沿岸画一条射线BF,在BF 上截取 过点 D作 并使E.C.A 在同一条直线上,则DE的长就是A,B间的距离,请你说明其中的道理。
23.(12分)如图20所示,将长方形纸片 ABCD 沿EF 折叠,使点 A 与点 C 重合,点 D 落在点G 处,EF 为折痕.
(1)试说明:
(2)若 求四这形 ECGF(阴影部分)的面积。
24.(12分)如图21①,已知 D 为∠BAC的平分线上一点.连接BD,CD,全等三角形的对数是 ;
如图20②,已知AB=AC,D,E 为. 的平分线上的两点,连接BD,CD,BE,CE,全等三角形的对数是多少
如图20③所示,已知AB=AC,D,E,F为 的平分线上的三点.连接BD,CD,BE,CE,BF,CF,全等三角形的对数是多少
……
依此规律,第 n个图形中全等三角形的对数是多少
1. D 2. A 3. B4. B5. C6. C7. C 8. A9. A 10. B
11.三角形的稳定性
12.513.40°14.4 米15.3
16.∠A=∠D(或∠E=∠F或CE=BF等)
17.①②③④18.180°
19.答案不唯一,如:
20.解:∵P为AB 的中点,∴PA=PB. 又∵∠A=∠B,∠MPA=∠NPB,∴△APM≌△BPN.
21.解:∵在△ABD 和△CBD 中, △ABD≌△CBD(SSS),∴∠ABD=∠CBD,又∵OE⊥AB,OF⊥CB,∴∠BEO=∠BFO=90°,又BO=BO.∴△BEO≌△BFO.∴OE=OF.
22.解:因为 DE∥AB,所以∠A=∠E,∠ABC=∠CDE(两直线平行,内错角相等),又因为 BC=CD(已知),所以△ABC≌△EDC(AAS),所以AB=DE(全等三角形的对应边相等)
23.解:(1)由题意知∠BCF =∠ECG=90°,所以∠GCF+∠FCE=90°,∠FCE+∠BCE=90°,所以∠GCF=∠BCE. 又因为∠G=∠B=90°,GC=BC,所以△FGC≌△ABC.
(2)由题意及(1)知四边形ECGF的面积=四边形AEFD 的面积=四边形FBCF 的面积 四边形ABCD的面积
24.解:题图①中,∵AD 是△BAC 的平分线,∴∠BAD = ∠CAD. 在△ABD 与△ACD 中,
∴题图①中有1对全等三角形.同理,题图②中,△ABE≌△ACE,
∴BE=EC.∵△ABD≌△ACD.
∴ BD = CD. 在 △BDE 和 △CDE 中,
HDESD,△BDE②△CDE(SSB),∴题图①
中有3对全等三角形,由此发现:第n个图形中全等三角形的对数是
(时间:120分钟 满分:120分)
题号 一 二 三 总分
得分
一、选择题(每小题3分,共30分)
1.如图1,下面四个手机应用图标中是轴对称图形的是 ( )
2.如图2所示的图形中成轴对称的有 ( )
A.1个 B.2个 C.3个 D.4个
3.如图3,线段AD是△ABC分成面积相等的两部分,则线段AD是 ( )
A.△ABC的角平分线 B.△ABC的中线
C.△ABC的高 D.以上都不对
4.在△ABC中. 则△ABC是 ( )
A.锐角三角形 B.钝角三角形 C.直角三角形 D.无法确定
5.如图4.如图所示,在方格纸中,以 AB为一边作△ABP,使之与△ABC全等,从P ,P ,P ,P 四个点中找出符合条件的点 P,则点 P有 ( )
A.1个 B.2个 C.3个 D.4个
6.如图5所示,线段AD与BC 相交于点O,连接AB、AC、BD,若 AC=BD,AD=BC,则下列结论中不正确的是 ( )
A.△ABC≌△BAD B.∠CAB=∠DBA C. OB=OC D.∠C=∠D
7.利用基本作图法,不能作出唯一三角形的是 ( )
A.已知两边及其夹角 B.已知两角及夹边
C.已知两边及一边的对角 D.已知三边
8.如图6,B,D,E,C四点共线.且 若 则 的度数为 ( )
D.65°
9.如图7,在△ABC中,∠A=30°,∠ABC=50°,∠ACB=100°,△EDC≌△ABC,且 A、C、D在同一条直线上,则∠BCE= ( )
A.20° B.30° C.40° D.50°
10.如图8,△ABC的底边边长BC=a,当顶点 A 沿 BC 边上的高AD 由A 向 D 移动到达 E 点时,若 则△ABC的面积将变为原来的 ( )
B. C. D.
二、填空题(每小题3分,共24分)
11.如图9所示,为了使一扇旧木门不变形,木工师傅在木门的背面加钉一根木条,这样做的道理是利用了
12.如图10 所示,为估计池塘岸边A,B 的距离,甲、乙二人在池塘的一侧取一点O,测得OA=15米,OB=10米,设A,B间的距离为x米,则x的取值范围是 .
13.如图11所示,在△ABC 中,∠B=46°,∠C=54°,AD平分∠BAC,交 BC于点 D,DE∥AB,变 AC 于点E.则 的大小是 .
14.如图12所示,太阳光线 AC与A'C'是平行的,AB 表示一棵松树的高,A'B'表示一棵杨树的高,同一时刻两棵树的影长相等(即 已知松树的高 AB=4米,则杨树的高
中小学教育资源及组卷应用平台
15.如图13所示,在△ABC中,已知∠1=∠2,BE=CD,AB=5,AE=2,则(
16.如图14 所示,A、B、C、D四点在一条直线上. 于C,FB⊥AD于B,若要使 则还需补充一个条件可以是 .(写出一种即可)
17.如图15 所示,是由我们熟悉的一些基本数学图形组成的,其中是轴对称图形的是 (填序号).
18.如图16所示,将△ABC三个角分别沿DE、HG、EF 翻折,三个顶点均落在点 O 处,则. 的度数为
三、解答题(共66分)
19.(10分)如图16 所示,在3×3的正方形网格中,有一个以格点为顶点的三角形(阴影部分),请你在图①②③中,分别画出一个与阴影三角形成轴对称且以格点为顶点的三角形,并将所画三角形涂上阴影.(注:所画的三个图不能重复)
20.(10分)如图17所示. P为AB的中点,点M 为射线AC上(不与点A 重合)的任意一点,连接MP,并使 P的延长线交射线 BD 于点 N. 试说明:
21.(10分)我们把两组邻边相等的四边形叫做“筝形”.如图18所示.四边形 ABCD 是一个筝形,其中 CB,AD=CD. 对角线AC,BD 相交于点O. 垂足分别是 E,F.试说明:(
22.(12分)如图19 所示,A,B 两个建筑物分别位于河的两岸,要测得它们之间的距离,可以从 B 出发沿岸画一条射线BF,在BF 上截取 过点 D作 并使E.C.A 在同一条直线上,则DE的长就是A,B间的距离,请你说明其中的道理。
23.(12分)如图20所示,将长方形纸片 ABCD 沿EF 折叠,使点 A 与点 C 重合,点 D 落在点G 处,EF 为折痕.
(1)试说明:
(2)若 求四这形 ECGF(阴影部分)的面积。
24.(12分)如图21①,已知 D 为∠BAC的平分线上一点.连接BD,CD,全等三角形的对数是 ;
如图20②,已知AB=AC,D,E 为. 的平分线上的两点,连接BD,CD,BE,CE,全等三角形的对数是多少
如图20③所示,已知AB=AC,D,E,F为 的平分线上的三点.连接BD,CD,BE,CE,BF,CF,全等三角形的对数是多少
……
依此规律,第 n个图形中全等三角形的对数是多少
1. D 2. A 3. B4. B5. C6. C7. C 8. A9. A 10. B
11.三角形的稳定性
12.5
16.∠A=∠D(或∠E=∠F或CE=BF等)
17.①②③④18.180°
19.答案不唯一,如:
20.解:∵P为AB 的中点,∴PA=PB. 又∵∠A=∠B,∠MPA=∠NPB,∴△APM≌△BPN.
21.解:∵在△ABD 和△CBD 中, △ABD≌△CBD(SSS),∴∠ABD=∠CBD,又∵OE⊥AB,OF⊥CB,∴∠BEO=∠BFO=90°,又BO=BO.∴△BEO≌△BFO.∴OE=OF.
22.解:因为 DE∥AB,所以∠A=∠E,∠ABC=∠CDE(两直线平行,内错角相等),又因为 BC=CD(已知),所以△ABC≌△EDC(AAS),所以AB=DE(全等三角形的对应边相等)
23.解:(1)由题意知∠BCF =∠ECG=90°,所以∠GCF+∠FCE=90°,∠FCE+∠BCE=90°,所以∠GCF=∠BCE. 又因为∠G=∠B=90°,GC=BC,所以△FGC≌△ABC.
(2)由题意及(1)知四边形ECGF的面积=四边形AEFD 的面积=四边形FBCF 的面积 四边形ABCD的面积
24.解:题图①中,∵AD 是△BAC 的平分线,∴∠BAD = ∠CAD. 在△ABD 与△ACD 中,
∴题图①中有1对全等三角形.同理,题图②中,△ABE≌△ACE,
∴BE=EC.∵△ABD≌△ACD.
∴ BD = CD. 在 △BDE 和 △CDE 中,
HDESD,△BDE②△CDE(SSB),∴题图①
中有3对全等三角形,由此发现:第n个图形中全等三角形的对数是
同课章节目录
