北师大版七年级下册第一次月考测试卷数学(含答案)
文档属性
| 名称 | 北师大版七年级下册第一次月考测试卷数学(含答案) |
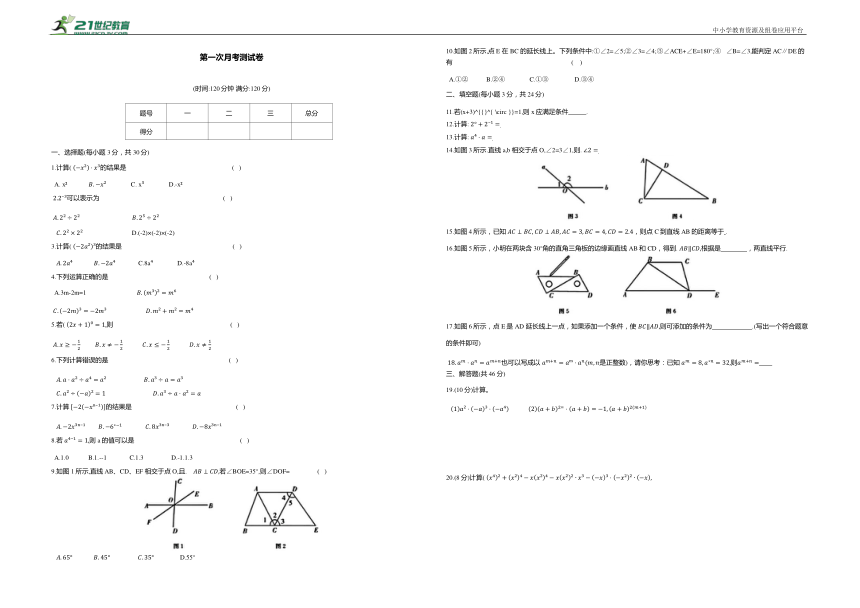
|
|
| 格式 | docx | ||
| 文件大小 | 240.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-08 00:00:00 | ||
图片预览

文档简介
第一次月考测试卷
(时间:120分钟 满分:120分)
题号 一 二 三 总分
得分
一、选择题(每小题3分,共30分)
1.计算( 的结果是 ( )
A. x C. x D.-x
可以表示为 ( )
D.(-2)×(-2)×(-2)
3.计算( 的结果是 ( )
C.8a D.-8a
4.下列运算正确的是 ( )
A.3m-2m=1
5.若( 则 ( )
6.下列计算错误的是 ( )
7.计算 的结果是 ( )
8.若 则a的值可以是 ( )
A.1.0 B.1.--1 C.1.3 D.-1.1.3
9.如图1所示,直线 AB、CD、EF 相交于点O,且. 若∠BOE=35°,则∠DOF= ( )
D.55°
10.如图2所示,点 E 在 BC 的延长线上。下列条件中:①∠2=∠5;②∠3=∠4;③∠ACE+∠E=180°;④ ∠B=∠3,能判定 AC∥DE的有 ( )
A.①② B.②④ C.①③ D.③④
二、填空题(每小题3分,共24分)
11.若(x+3)^{{}^{ \circ }}=1,则x应满足条件 .
12.计算:
13.计算:
14.如图3所示.直线a,b相交于点O,∠2=3∠1,则.
15.如图4所示,已知 ,则点 C到直线AB的距离等于 .
16.如图 5所示,小明在两块含 30°角的直角三角板的边缘画直线AB 和CD,得到. 根据是 ,两直线平行.
17.如图6所示,点 E是AD 延长线上一点,如果添加一个条件,使 则可添加的条件为 .(写出一个符合题意的条件即可)
也可以写成以 是正整数),请你思考:已知 则
三、解答题(共46分)
19.(10分)计算。
中小学教育资源及组卷应用平台
20.(8分)计算(
21.(8分)已知 求 的值.
22.(14分)如图7所示,AB、CD、EF 相交于点O,如果
(1)求 的度数;
(2)通过计算 的度数,你能发现射线OA 有什么特殊性
23.(12分)已知:如图8所示, 和 互余, 于点G.求证:
24.(12分)如图9所示,直线AB、CD 被直线EF 所截,H为CD 与EF 的交点, 于点H, 求证:
1. B 2. A 3. D 4. B
5. B〔提示:若( 则2x+1≠0,所以x≠﹣ .)
6. B〔提示:A. C. D计算结果正确;B.应为 a .〕
7. C〔提示:原式
8. D〔提示:①当a-3=0时,解得a=3,此时, =1.②当a=1时, ③当a=-1时, 所以a的值可以是-1.1,3.)
9. D 10. C
11. x≠-3(提示:因为( 所以x+3≠0,解得x≠-3.〕
12. 〔提示:原式
14.135° 15.2.4 16.内错角相等
17.∠A+∠ABC=180°(答案不唯一)
18.256〔提示:因为a"=8,a"=32,所以, =8×32=256.〕
19.解:(1)原式 (2)原式=(a+
20.解 .x°.
21.解: 所以1+5m=21,所以m=4,所以(
22.解:(1)因为∠AOC=65°,所以∠BOD=∠AOC=65°. 又因为∠BOE+∠BOD+∠DOF=180°,所以 (2)因为∠AOF=∠BOE=65°,且∠AOC=65°,所以∠AOF=∠AOC,所以射线OA 是∠COF 的平分线.
23.解:∵BE⊥FD,∴∠EGD=90°.∴∠1+∠D=90°,又∠2和∠D 互余,即∠2+∠D=90°,∴∠1=∠2,又∠C=∠1,∴∠C=∠2,∴AB∥CD.
24.解:如右图所示.∵GH⊥CD(已知):∴∠CHG=90°(垂直定义):A.又∵∠2=30°(已知),∴∠3=60°.∴∠4=60°(对顶角相等). 又∵∠1C.=60°(已知),∴∠1=∠4.∴AB∥CD(同位角相等,两直线平行).
(时间:120分钟 满分:120分)
题号 一 二 三 总分
得分
一、选择题(每小题3分,共30分)
1.计算( 的结果是 ( )
A. x C. x D.-x
可以表示为 ( )
D.(-2)×(-2)×(-2)
3.计算( 的结果是 ( )
C.8a D.-8a
4.下列运算正确的是 ( )
A.3m-2m=1
5.若( 则 ( )
6.下列计算错误的是 ( )
7.计算 的结果是 ( )
8.若 则a的值可以是 ( )
A.1.0 B.1.--1 C.1.3 D.-1.1.3
9.如图1所示,直线 AB、CD、EF 相交于点O,且. 若∠BOE=35°,则∠DOF= ( )
D.55°
10.如图2所示,点 E 在 BC 的延长线上。下列条件中:①∠2=∠5;②∠3=∠4;③∠ACE+∠E=180°;④ ∠B=∠3,能判定 AC∥DE的有 ( )
A.①② B.②④ C.①③ D.③④
二、填空题(每小题3分,共24分)
11.若(x+3)^{{}^{ \circ }}=1,则x应满足条件 .
12.计算:
13.计算:
14.如图3所示.直线a,b相交于点O,∠2=3∠1,则.
15.如图4所示,已知 ,则点 C到直线AB的距离等于 .
16.如图 5所示,小明在两块含 30°角的直角三角板的边缘画直线AB 和CD,得到. 根据是 ,两直线平行.
17.如图6所示,点 E是AD 延长线上一点,如果添加一个条件,使 则可添加的条件为 .(写出一个符合题意的条件即可)
也可以写成以 是正整数),请你思考:已知 则
三、解答题(共46分)
19.(10分)计算。
中小学教育资源及组卷应用平台
20.(8分)计算(
21.(8分)已知 求 的值.
22.(14分)如图7所示,AB、CD、EF 相交于点O,如果
(1)求 的度数;
(2)通过计算 的度数,你能发现射线OA 有什么特殊性
23.(12分)已知:如图8所示, 和 互余, 于点G.求证:
24.(12分)如图9所示,直线AB、CD 被直线EF 所截,H为CD 与EF 的交点, 于点H, 求证:
1. B 2. A 3. D 4. B
5. B〔提示:若( 则2x+1≠0,所以x≠﹣ .)
6. B〔提示:A. C. D计算结果正确;B.应为 a .〕
7. C〔提示:原式
8. D〔提示:①当a-3=0时,解得a=3,此时, =1.②当a=1时, ③当a=-1时, 所以a的值可以是-1.1,3.)
9. D 10. C
11. x≠-3(提示:因为( 所以x+3≠0,解得x≠-3.〕
12. 〔提示:原式
14.135° 15.2.4 16.内错角相等
17.∠A+∠ABC=180°(答案不唯一)
18.256〔提示:因为a"=8,a"=32,所以, =8×32=256.〕
19.解:(1)原式 (2)原式=(a+
20.解 .x°.
21.解: 所以1+5m=21,所以m=4,所以(
22.解:(1)因为∠AOC=65°,所以∠BOD=∠AOC=65°. 又因为∠BOE+∠BOD+∠DOF=180°,所以 (2)因为∠AOF=∠BOE=65°,且∠AOC=65°,所以∠AOF=∠AOC,所以射线OA 是∠COF 的平分线.
23.解:∵BE⊥FD,∴∠EGD=90°.∴∠1+∠D=90°,又∠2和∠D 互余,即∠2+∠D=90°,∴∠1=∠2,又∠C=∠1,∴∠C=∠2,∴AB∥CD.
24.解:如右图所示.∵GH⊥CD(已知):∴∠CHG=90°(垂直定义):A.又∵∠2=30°(已知),∴∠3=60°.∴∠4=60°(对顶角相等). 又∵∠1C.=60°(已知),∴∠1=∠4.∴AB∥CD(同位角相等,两直线平行).
同课章节目录
