北师大七下数学 用图象表示的变量之间的关系专题测试卷(二)
文档属性
| 名称 | 北师大七下数学 用图象表示的变量之间的关系专题测试卷(二) |
|
|
| 格式 | docx | ||
| 文件大小 | 859.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-08 00:00:00 | ||
图片预览

文档简介
用图象表示的变量之间的关系专题测试卷(二)
(时间:120分钟 满分:120分)
题号 一 二 三 总分
得分
一、选择题(每小题4分,共24分)
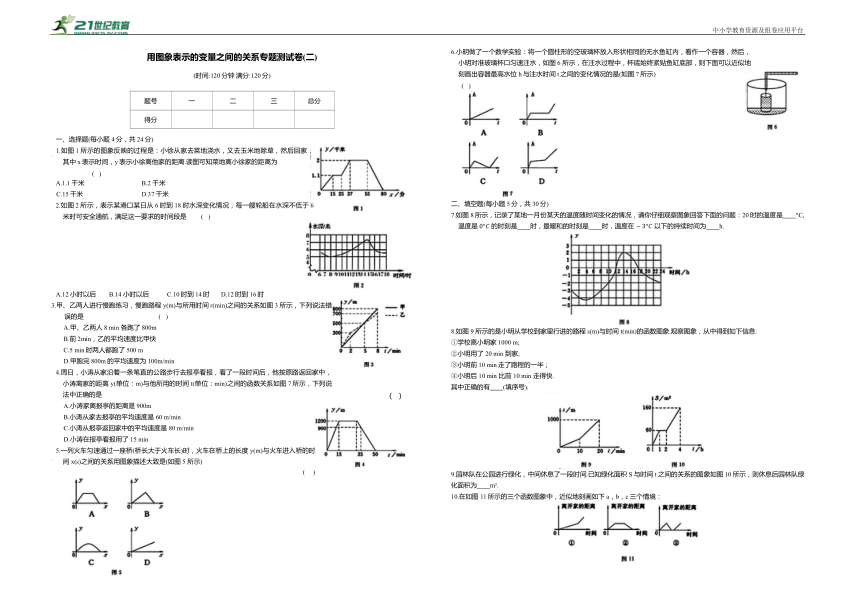
1.如图1所示的图象反映的过程是:小徐从家去菜地浇水,又去玉米地除草,然后回家,其中x表示时间,y表示小徐离他家的距离.读图可知菜地离小徐家的距离为 ( )
A.1.1千米 B.2 千米
C.15千米 D.37千米
2.如图2所示,表示某港口某日从6时到18时水深变化情况,每一艘轮船在水深不低于6米时可安全通航,满足这一要求的时间段是 ( )
A.12小时以后 B.14 小时以后 C.10时到14时 D.12时到16时
3.甲、乙两人进行慢跑练习,慢跑路程y(m)与所用时间r(min)之间的关系如图3所示,下列说法错误的是 ( )
A.甲、乙两人8 min 各跑了 800m
B.前2min,乙的平均速度比甲快
C.5 min时两人都跑了 500 m
D.甲跑完 800m的平均速度为100m/min
4.周日,小涛从家沿着一条笔直的公路步行去报亭看报,看了一段时间后,他按原路返回家中,小涛离家的距离y(单位:m)与他所用的时间t(单位:min)之间的函数关系如图7所示,下列说法中正确的是
A.小涛家离报亭的距离是900m
B.小涛从家去报亭的平均速度是60 m/min
C.小涛从报亭返回家中的平均速度是80 m/min
D.小涛在报亭看报用了 15 min
5.一列火车匀速通过一座桥(桥长大于火车长)时,火车在桥上的长度 y(m)与火车进入桥的时间x(s)之间的关系用图象描述大致是(如图5 所示)
( )
6.小明做了一个数学实验:将一个圆柱形的空玻璃杯放入形状相同的无水鱼缸内,看作一个容器,然后,小明对准玻璃杯口匀速注水,如图6 所示,在注水过程中,杯底始终紧贴鱼缸底部,则下面可以近似地刻画出容器最高水位h与注水时间t之间的变化情况的是(如图7所示) ( )
二、填空题(每小题5分,共30分)
7.如图8所示,记录了某地一月份某天的温度随时间变化的情况,请你仔细观察图象回答下面的问题:20时的温度是 °C,温度是 的时刻是 时,最暖和的时刻是 时,温度在 以下的持续时间为 h.
8.如图9 所示的是小明从学校到家里行进的路程s(m)与时间t(min)的函数图象.观察图象,从中得到如下信息:
①学校离小明家1000 m;
②小明用了 20 min 到家;
③小明前10 min走了路程的一半;
④小明后 10 min 比前 10 min 走得快.
其中正确的有 (填序号).
9.园林队在公园进行绿化,中间休息了一段时间.已知绿化面积S与时间t之间的关系的图象如图10所示,则休息后园林队绿化面积为 m .
10.在如图11所示的三个函数图象中,近似地刻画如下a,b,c三个情境:
中小学教育资源及组卷应用平台
情境a:小芳离开家不久,发现把作业本忘在家里,于是返回了家里找到了作业本再去学校.
情境b:小芳从家出发,走了一段路程后,为了赶时间,以更快的速度前进.
情境c:小芳从家出发,到学校上学,放学回到了家.
情境a,b,c所对应的图象分别是 .(按次序填写a,b,c对应的序号)
11.如图12所示的是甲、乙两人同一地点出发后,路程随时间变化的图象.
(1)甲的速度 乙的速度;(填“大于”“等于”或“小于”)
(2)甲、乙二人在 时相遇;
(3)路程为1500km时,甲行驶了 h,乙行驶了 h.
12.某出租车公司的收费标准如图13 所示,其中x(km)表示行驶里程,y(元)表示车费,若乘客在打车后付费42元,则该乘客乘坐出租车行驶了 km.
三、解答题(共66分)
13.(15 分)一天之中,海水的水深是不同的,如图14 所示的是某港口从0时到12时的水深情况,结合图象回答下列问题:
(1)图中描述了哪两个变量之间的关系 其中自变量是什么 因变量是什么
(2)大约什么时刻港口的水最深 深度约是多少
(3)图中A 点表示的是什么
(4)在什么时间范围内,水深在增加 什么时间范围内,水深在减少
14.(15 分)小明骑单车上学,当他骑了一段路时,想起要买某本书,于是又折回到刚经过的某书店,买到书后继续去学校,图15 是他本次上学所用的时间与路程的关系示意图.根据图中提供的信息回答下列问题:
(1)小明家到学校的路程是多少米
(2)在整个上学的途中,哪个时间段小明骑车速度最快 最快的速度是多少
(3)小明在书店停留了多少分钟
(4)本次上学途中,小明一共行驶了多少米 一共用了多少分钟
15.(18分)图16(1)中的摩天轮可抽象成一个圆,圆上一点离地面的高度 y(m)与旋转时间x(min)之间的关系如图16(2)所示,根据图中的信息回答问题.
(1)根据图23(2)补全表格;
旋转时间x/min 0 3 6 8 12 ***
高度y/m 5 5 5
(2)表中反映的两个变量中,自变量是 ,因变量是 ;
(3)根据图象,求摩天轮的直径,它旋转一周需要多长时间
16.(18分)已知动点 P以每秒2cm的速度沿如图17(1)所示的边框按从B→C→D→E→F→A的路径移动。相应的 的面积S关于时间t的图象如图(2)所示,若 试回答下列问题.
(1)动点 P 在线段 上运动的过程中, 的面积S 保持不变.
(m
(3)求出图(2)中的a与b的值.
(4)在上述运动过程中,求出 面积的最大值.
1. A 2. D
3. A〔提示:由图可得甲8 min跑了800m,乙8 min跑了 700m,故选项A 错误.〕
4. D 5. A 6. D
7.-1 12.18 14 8 8.①②④ 9.100
10.③①②
11.(1)小于 (2)6 (3)9 4
12.25〔提示:因为42元>9元,根据图形可知,当行程大于3km时,每增加1km,乘车费增加(12-9)÷(5-3)=1.5(元),乘车费与行驶里程的关系式为 当y=42时,x=25.)
13.解:(1)反映了水深和时间之间的关系,其中时间是自变量,水深是因变量. (2)3时港口的水最深,深度约是7米. (3)图中 A 点表示的是6时港口的水深。(4)从0时到3时及从9时到12时水深在增加,从3时到9时水深在减少。
14.解:(1)根据图象,小明家到学校的路程是 1500米. (2)根据图象,12≤x≤14时,直线最陡,故小明在12 分~14 分最快,速度为 (米/分). (3)根据题意,小明在书店停留的时间为从8分到12 分,故小明在书店停留了4 分.
(4)小明共行驶了1200+600+900=2700(米),共用了14分。
15.解:(1)由图象可知,当x=3时,y=70,当x=8时,y=54. (2)反映的两个变量中,自变量是旋转时间x,因变量是高度 y. (3)由图象可知摩天轮的直径为70-5=65(m),旋转一周需要的时间为 6 min.
16.解:(1)动点 P 在线段CD 和EF 上运动的过程中△ABP的面积S保持不变. (2)已知当P在BC上时,以AB为底的高在不断增大,到达点 C时,开始不变,由图(2)得 P 在BC 上移动了4s,那么BC=4×2=8(cm).在CD上移动了2 s,CD=2×2=4(cm),在 DE上移动了3s,DE=3×2=6(cm),而 AB=6 cm,那么 EF=AB--CD=2(cm). (3)由图(2)得 a 是点 P 运行 4 s 时△ABP的面积,所以 (cm ). b为点P 走完全程的时间:t=9+1+7=17(s). (4)因为点 P 移动到点 E 时而积达到最大值,所以 ,因为AB=6 cm,BC=8cm,DE=6cm,所以 42(cm ).
(时间:120分钟 满分:120分)
题号 一 二 三 总分
得分
一、选择题(每小题4分,共24分)
1.如图1所示的图象反映的过程是:小徐从家去菜地浇水,又去玉米地除草,然后回家,其中x表示时间,y表示小徐离他家的距离.读图可知菜地离小徐家的距离为 ( )
A.1.1千米 B.2 千米
C.15千米 D.37千米
2.如图2所示,表示某港口某日从6时到18时水深变化情况,每一艘轮船在水深不低于6米时可安全通航,满足这一要求的时间段是 ( )
A.12小时以后 B.14 小时以后 C.10时到14时 D.12时到16时
3.甲、乙两人进行慢跑练习,慢跑路程y(m)与所用时间r(min)之间的关系如图3所示,下列说法错误的是 ( )
A.甲、乙两人8 min 各跑了 800m
B.前2min,乙的平均速度比甲快
C.5 min时两人都跑了 500 m
D.甲跑完 800m的平均速度为100m/min
4.周日,小涛从家沿着一条笔直的公路步行去报亭看报,看了一段时间后,他按原路返回家中,小涛离家的距离y(单位:m)与他所用的时间t(单位:min)之间的函数关系如图7所示,下列说法中正确的是
A.小涛家离报亭的距离是900m
B.小涛从家去报亭的平均速度是60 m/min
C.小涛从报亭返回家中的平均速度是80 m/min
D.小涛在报亭看报用了 15 min
5.一列火车匀速通过一座桥(桥长大于火车长)时,火车在桥上的长度 y(m)与火车进入桥的时间x(s)之间的关系用图象描述大致是(如图5 所示)
( )
6.小明做了一个数学实验:将一个圆柱形的空玻璃杯放入形状相同的无水鱼缸内,看作一个容器,然后,小明对准玻璃杯口匀速注水,如图6 所示,在注水过程中,杯底始终紧贴鱼缸底部,则下面可以近似地刻画出容器最高水位h与注水时间t之间的变化情况的是(如图7所示) ( )
二、填空题(每小题5分,共30分)
7.如图8所示,记录了某地一月份某天的温度随时间变化的情况,请你仔细观察图象回答下面的问题:20时的温度是 °C,温度是 的时刻是 时,最暖和的时刻是 时,温度在 以下的持续时间为 h.
8.如图9 所示的是小明从学校到家里行进的路程s(m)与时间t(min)的函数图象.观察图象,从中得到如下信息:
①学校离小明家1000 m;
②小明用了 20 min 到家;
③小明前10 min走了路程的一半;
④小明后 10 min 比前 10 min 走得快.
其中正确的有 (填序号).
9.园林队在公园进行绿化,中间休息了一段时间.已知绿化面积S与时间t之间的关系的图象如图10所示,则休息后园林队绿化面积为 m .
10.在如图11所示的三个函数图象中,近似地刻画如下a,b,c三个情境:
中小学教育资源及组卷应用平台
情境a:小芳离开家不久,发现把作业本忘在家里,于是返回了家里找到了作业本再去学校.
情境b:小芳从家出发,走了一段路程后,为了赶时间,以更快的速度前进.
情境c:小芳从家出发,到学校上学,放学回到了家.
情境a,b,c所对应的图象分别是 .(按次序填写a,b,c对应的序号)
11.如图12所示的是甲、乙两人同一地点出发后,路程随时间变化的图象.
(1)甲的速度 乙的速度;(填“大于”“等于”或“小于”)
(2)甲、乙二人在 时相遇;
(3)路程为1500km时,甲行驶了 h,乙行驶了 h.
12.某出租车公司的收费标准如图13 所示,其中x(km)表示行驶里程,y(元)表示车费,若乘客在打车后付费42元,则该乘客乘坐出租车行驶了 km.
三、解答题(共66分)
13.(15 分)一天之中,海水的水深是不同的,如图14 所示的是某港口从0时到12时的水深情况,结合图象回答下列问题:
(1)图中描述了哪两个变量之间的关系 其中自变量是什么 因变量是什么
(2)大约什么时刻港口的水最深 深度约是多少
(3)图中A 点表示的是什么
(4)在什么时间范围内,水深在增加 什么时间范围内,水深在减少
14.(15 分)小明骑单车上学,当他骑了一段路时,想起要买某本书,于是又折回到刚经过的某书店,买到书后继续去学校,图15 是他本次上学所用的时间与路程的关系示意图.根据图中提供的信息回答下列问题:
(1)小明家到学校的路程是多少米
(2)在整个上学的途中,哪个时间段小明骑车速度最快 最快的速度是多少
(3)小明在书店停留了多少分钟
(4)本次上学途中,小明一共行驶了多少米 一共用了多少分钟
15.(18分)图16(1)中的摩天轮可抽象成一个圆,圆上一点离地面的高度 y(m)与旋转时间x(min)之间的关系如图16(2)所示,根据图中的信息回答问题.
(1)根据图23(2)补全表格;
旋转时间x/min 0 3 6 8 12 ***
高度y/m 5 5 5
(2)表中反映的两个变量中,自变量是 ,因变量是 ;
(3)根据图象,求摩天轮的直径,它旋转一周需要多长时间
16.(18分)已知动点 P以每秒2cm的速度沿如图17(1)所示的边框按从B→C→D→E→F→A的路径移动。相应的 的面积S关于时间t的图象如图(2)所示,若 试回答下列问题.
(1)动点 P 在线段 上运动的过程中, 的面积S 保持不变.
(m
(3)求出图(2)中的a与b的值.
(4)在上述运动过程中,求出 面积的最大值.
1. A 2. D
3. A〔提示:由图可得甲8 min跑了800m,乙8 min跑了 700m,故选项A 错误.〕
4. D 5. A 6. D
7.-1 12.18 14 8 8.①②④ 9.100
10.③①②
11.(1)小于 (2)6 (3)9 4
12.25〔提示:因为42元>9元,根据图形可知,当行程大于3km时,每增加1km,乘车费增加(12-9)÷(5-3)=1.5(元),乘车费与行驶里程的关系式为 当y=42时,x=25.)
13.解:(1)反映了水深和时间之间的关系,其中时间是自变量,水深是因变量. (2)3时港口的水最深,深度约是7米. (3)图中 A 点表示的是6时港口的水深。(4)从0时到3时及从9时到12时水深在增加,从3时到9时水深在减少。
14.解:(1)根据图象,小明家到学校的路程是 1500米. (2)根据图象,12≤x≤14时,直线最陡,故小明在12 分~14 分最快,速度为 (米/分). (3)根据题意,小明在书店停留的时间为从8分到12 分,故小明在书店停留了4 分.
(4)小明共行驶了1200+600+900=2700(米),共用了14分。
15.解:(1)由图象可知,当x=3时,y=70,当x=8时,y=54. (2)反映的两个变量中,自变量是旋转时间x,因变量是高度 y. (3)由图象可知摩天轮的直径为70-5=65(m),旋转一周需要的时间为 6 min.
16.解:(1)动点 P 在线段CD 和EF 上运动的过程中△ABP的面积S保持不变. (2)已知当P在BC上时,以AB为底的高在不断增大,到达点 C时,开始不变,由图(2)得 P 在BC 上移动了4s,那么BC=4×2=8(cm).在CD上移动了2 s,CD=2×2=4(cm),在 DE上移动了3s,DE=3×2=6(cm),而 AB=6 cm,那么 EF=AB--CD=2(cm). (3)由图(2)得 a 是点 P 运行 4 s 时△ABP的面积,所以 (cm ). b为点P 走完全程的时间:t=9+1+7=17(s). (4)因为点 P 移动到点 E 时而积达到最大值,所以 ,因为AB=6 cm,BC=8cm,DE=6cm,所以 42(cm ).
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
