5.2.1实际问题的函数刻画5.2.2用函数模型解决实际问题课件(共46张PPT) 2023-2024学年高一数学北师大版(2019)必修一
文档属性
| 名称 | 5.2.1实际问题的函数刻画5.2.2用函数模型解决实际问题课件(共46张PPT) 2023-2024学年高一数学北师大版(2019)必修一 |

|
|
| 格式 | pptx | ||
| 文件大小 | 7.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-07 00:00:00 | ||
图片预览











文档简介
(共46张PPT)
§2 实际问题中的函数模型
2.1 实际问题的函数刻画
2.2 用函数模型解决实际问题
1.体会实际问题中建立函数模型的过程,进一步掌握常用的函数模型,提升数学抽象的核心素养.
2.通过建立函数模型解决实际问题的过程,提升数学建模的核心素养.
学习目标
1
知识梳理
自主探究
1.常见的几类函数模型
函数模型 函数解析式
一次函数模型 f(x)=ax+b(a,b为常数,a≠0)
二次函数模型 f(x)=ax2+bx+c(a,b,c为常数,
a≠0)
指数函数模型 f(x)=bax+c(a,b,c为常数,a>0,且a≠1,b≠0)
2.建立函数模型解决实际问题的步骤
(1)确切理解题意,明确问题的实际背景,进行科学的抽象、概括,将实际问题转化为数学问题;
(2)建立相应的函数模型;
(3)求解函数模型,得出数学结论;
(4)将用数学知识和方法得出的结论,还原为实际问题的意义,并进行验证,看是否符合实际.
2
师生互动
合作探究
利用图象刻画变化过程
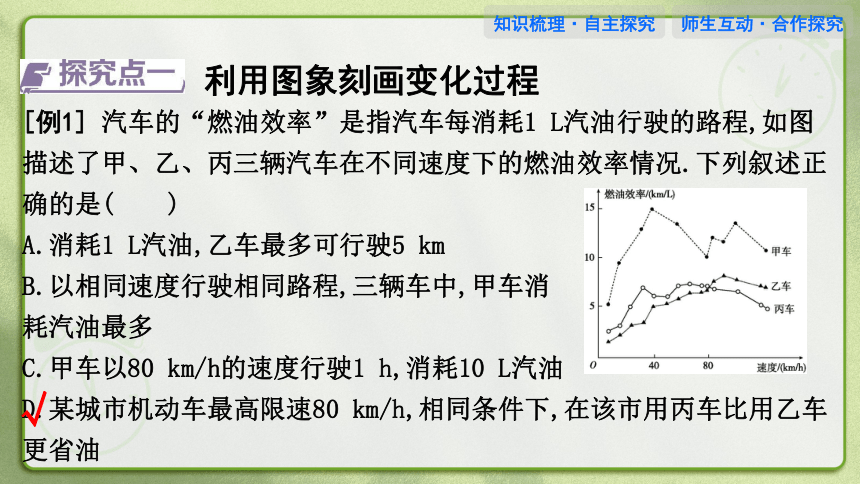
[例1] 汽车的“燃油效率”是指汽车每消耗1 L汽油行驶的路程,如图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况.下列叙述正确的是( )
A.消耗1 L汽油,乙车最多可行驶5 km
B.以相同速度行驶相同路程,三辆车中,甲车消
耗汽油最多
C.甲车以80 km/h的速度行驶1 h,消耗10 L汽油
D.某城市机动车最高限速80 km/h,相同条件下,在该市用丙车比用乙车更省油
√
解析:根据图象知消耗1 L汽油,乙车最多行驶路程大于5 km,故选项A错误;以相同速度行驶时,甲车燃油效率最高,因此以相同速度行驶相同路程时,甲车消耗汽油最少,故选项B错误;甲车以80 km/h的速度行驶时燃油效率为10 km/L,行驶1 h,路程为80 km,消耗8 L汽油,故选项C错误;最高限速80 km/h,丙车的燃油效率比乙车高,因此相同条件下,在该市用丙车比用乙车更省油,故选项D正确.故选D.
判断函数图象与实际问题变化过程相吻合的两种方法
(1)构建函数模型法:当根据题意易构建函数模型时,先建立函数模型,再结合模型选图象.
(2)验证法:根据实际问题中两变量的变化快慢等特点,结合图象的变化趋势,验证是否吻合,从中排除不符合实际的情况,选出符合实际情况的答案.
针对训练:设甲、乙两地的距离为a(a>0),某人骑自行车匀速从甲地到乙地用了20分钟,在乙地休息10分钟后,他又匀速从乙地返回到甲地用了30分钟,则此人从出发到返回原地所经过的路程y和其所用的时间x的函数图象为( )
√
解析:y为此人从出发到返回原地所经过的路程,而不是位移,故排除A,C;又因为此人在乙地休息10分钟,故排除B.故选D.
构建函数模型解决实际问题
角度1 二次函数、分段函数模型
(2)求年产量为多少万斤时,该镇所获利润最大 求出利润最大值.
(1)实际问题中有些变量间的关系不能用同一个关系式给出,而是由几个不同的关系式构成,因此需要构建分段函数模型;分段函数的最值是各段最大值(或最小值)中的最大者(或最小者).
(2)二次函数是常用的函数模型,建立二次函数模型可以求出函数的值域或最值.解决实际中的优化问题时,一定要分析自变量的取值范围.利用配方法求最值时,一定要注意对称轴与给定区间的关系.
(2)当月产量为何值时,公司所获利润最大 最大利润为多少元 (总收益=总成本+利润)
②当x>400时,f(x)=-100x+60 000为减函数,
所以f(x)<-100×400+60 000=20 000<25 000.
所以当月产量为300台时,利润最大,最大利润为25 000元.
角度2 指数函数模型
[例3] 某大学2020年在校本科生4 500人,研究生500人,预计在今后若干年内,该学校本科生每年比上一年增长12.5%,研究生每年比上一年增长50%,则从 年开始该校研究生的人数占该校本科生和研究生总人数的比例达到50%以上.(参考数据:lg 2≈0.301 0,lg 3≈
0.477 1)
2028
增长率问题,在实际问题中常可以用指数函数模型y=N(1+p)x(其中N是基础数,p为增长率,x为时间)或幂函数模型y=a(1+x)n(其中a为基础数,x为增长率,n为时间)的形式表示.求解时要注意指数式、对数式的互化以及指数函数、对数函数的单调性的应用.
√
角度3 对数函数模型
[例4] 核酸检测分析是用荧光定量PCR法,通过化学物质的荧光信号,对在PCR扩增进程中成指数级增加的靶标DNA实时检测,在PCR扩增的指数时期,荧光信号强度达到阈值时,DNA的数量Xn与扩增次数n满足:lg Xn=nlg(1+p)+lg X0,其中p为扩增效率,X0为DNA的初始数量.已知某被测标本DNA扩增5次后,数量变为原来的10倍,那么该标本的扩增效率p约为(参考数据:100.2≈1.585,10-0.2≈
0.631)( )
A.0.369 B.0.415 C.0.585 D.0.631
√
涉及对数函数有关的函数模型问题,应结合函数解析式以及对数函数的运算性质以及对数函数的性质求解.求解时注意指数式与对数式的互化,以及实际问题中的条件限制.
√
1.若一根蜡烛长20 cm,点燃后每小时燃烧5 cm,则燃烧剩下的高度h(cm)与燃烧时间t(h)的函数关系用图象表示为( )
解析:由题意可知h=20-5t(0≤t≤4),所以其图象为B.故选B.
1
2
3
4
√
1
2
3
4
2.某单位为鼓励职工节约用水,作出如下规定:每位职工每月用水不超过10 m3的,按3元/m3收费;用水超过10 m3的,超过的部分按5元/m3收费.某职工某月缴水费55元,则该职工这个月实际用水为( )
A.13 m3 B.14 m3
C.15 m3 D.16 m3
√
1
2
3
4
1
2
3
4
√
1
2
3
4
4.已知某种食品的保鲜时间y(单位:h)与储藏温度x(单位:℃)之间满足函数关系y=a·2bx.若该食品在4 ℃时保鲜时间为192 h,在12 ℃时保鲜时间为48 h,则该食品在28 ℃时保鲜时间为( )
A.2 h B.3 h
C.4 h D.6 h
1
2
3
4
√
1
2
3
4
√
√
[例3] 一个车辆制造厂引进了一条摩托车整车装配流水线,这条流水线生产的摩托车数量x(辆)与创造的价值y
(元)之间满足二次函数关系.已知当产量为0时,创造的价值也为0;当产量为55辆时,创造的价值达到最大
6 050元.若这家工厂希望利用这条流水线创收达到
6 000元及以上,则它应该生产的摩托车数量至少是
.
50辆
解析:由题意,设摩托车数量x(辆)与创造的价值y(元)之间满足二次函数y=a(x-55)2+6 050(a<0),又当x=0时,y=0,所以a=-2,故y=-2x2+220x,则-2x2+220x≥
6 000,解得50≤x≤60.
(2)已知该地下车库的面积为2 560 m2,当积水深度小于等于
0.05 m时,小区居民方可入内,那么从消防部门开始排水时算起,至少需要经过几个小时以后,小区居民才能进入地下车库
§2 实际问题中的函数模型
2.1 实际问题的函数刻画
2.2 用函数模型解决实际问题
1.体会实际问题中建立函数模型的过程,进一步掌握常用的函数模型,提升数学抽象的核心素养.
2.通过建立函数模型解决实际问题的过程,提升数学建模的核心素养.
学习目标
1
知识梳理
自主探究
1.常见的几类函数模型
函数模型 函数解析式
一次函数模型 f(x)=ax+b(a,b为常数,a≠0)
二次函数模型 f(x)=ax2+bx+c(a,b,c为常数,
a≠0)
指数函数模型 f(x)=bax+c(a,b,c为常数,a>0,且a≠1,b≠0)
2.建立函数模型解决实际问题的步骤
(1)确切理解题意,明确问题的实际背景,进行科学的抽象、概括,将实际问题转化为数学问题;
(2)建立相应的函数模型;
(3)求解函数模型,得出数学结论;
(4)将用数学知识和方法得出的结论,还原为实际问题的意义,并进行验证,看是否符合实际.
2
师生互动
合作探究
利用图象刻画变化过程
[例1] 汽车的“燃油效率”是指汽车每消耗1 L汽油行驶的路程,如图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况.下列叙述正确的是( )
A.消耗1 L汽油,乙车最多可行驶5 km
B.以相同速度行驶相同路程,三辆车中,甲车消
耗汽油最多
C.甲车以80 km/h的速度行驶1 h,消耗10 L汽油
D.某城市机动车最高限速80 km/h,相同条件下,在该市用丙车比用乙车更省油
√
解析:根据图象知消耗1 L汽油,乙车最多行驶路程大于5 km,故选项A错误;以相同速度行驶时,甲车燃油效率最高,因此以相同速度行驶相同路程时,甲车消耗汽油最少,故选项B错误;甲车以80 km/h的速度行驶时燃油效率为10 km/L,行驶1 h,路程为80 km,消耗8 L汽油,故选项C错误;最高限速80 km/h,丙车的燃油效率比乙车高,因此相同条件下,在该市用丙车比用乙车更省油,故选项D正确.故选D.
判断函数图象与实际问题变化过程相吻合的两种方法
(1)构建函数模型法:当根据题意易构建函数模型时,先建立函数模型,再结合模型选图象.
(2)验证法:根据实际问题中两变量的变化快慢等特点,结合图象的变化趋势,验证是否吻合,从中排除不符合实际的情况,选出符合实际情况的答案.
针对训练:设甲、乙两地的距离为a(a>0),某人骑自行车匀速从甲地到乙地用了20分钟,在乙地休息10分钟后,他又匀速从乙地返回到甲地用了30分钟,则此人从出发到返回原地所经过的路程y和其所用的时间x的函数图象为( )
√
解析:y为此人从出发到返回原地所经过的路程,而不是位移,故排除A,C;又因为此人在乙地休息10分钟,故排除B.故选D.
构建函数模型解决实际问题
角度1 二次函数、分段函数模型
(2)求年产量为多少万斤时,该镇所获利润最大 求出利润最大值.
(1)实际问题中有些变量间的关系不能用同一个关系式给出,而是由几个不同的关系式构成,因此需要构建分段函数模型;分段函数的最值是各段最大值(或最小值)中的最大者(或最小者).
(2)二次函数是常用的函数模型,建立二次函数模型可以求出函数的值域或最值.解决实际中的优化问题时,一定要分析自变量的取值范围.利用配方法求最值时,一定要注意对称轴与给定区间的关系.
(2)当月产量为何值时,公司所获利润最大 最大利润为多少元 (总收益=总成本+利润)
②当x>400时,f(x)=-100x+60 000为减函数,
所以f(x)<-100×400+60 000=20 000<25 000.
所以当月产量为300台时,利润最大,最大利润为25 000元.
角度2 指数函数模型
[例3] 某大学2020年在校本科生4 500人,研究生500人,预计在今后若干年内,该学校本科生每年比上一年增长12.5%,研究生每年比上一年增长50%,则从 年开始该校研究生的人数占该校本科生和研究生总人数的比例达到50%以上.(参考数据:lg 2≈0.301 0,lg 3≈
0.477 1)
2028
增长率问题,在实际问题中常可以用指数函数模型y=N(1+p)x(其中N是基础数,p为增长率,x为时间)或幂函数模型y=a(1+x)n(其中a为基础数,x为增长率,n为时间)的形式表示.求解时要注意指数式、对数式的互化以及指数函数、对数函数的单调性的应用.
√
角度3 对数函数模型
[例4] 核酸检测分析是用荧光定量PCR法,通过化学物质的荧光信号,对在PCR扩增进程中成指数级增加的靶标DNA实时检测,在PCR扩增的指数时期,荧光信号强度达到阈值时,DNA的数量Xn与扩增次数n满足:lg Xn=nlg(1+p)+lg X0,其中p为扩增效率,X0为DNA的初始数量.已知某被测标本DNA扩增5次后,数量变为原来的10倍,那么该标本的扩增效率p约为(参考数据:100.2≈1.585,10-0.2≈
0.631)( )
A.0.369 B.0.415 C.0.585 D.0.631
√
涉及对数函数有关的函数模型问题,应结合函数解析式以及对数函数的运算性质以及对数函数的性质求解.求解时注意指数式与对数式的互化,以及实际问题中的条件限制.
√
1.若一根蜡烛长20 cm,点燃后每小时燃烧5 cm,则燃烧剩下的高度h(cm)与燃烧时间t(h)的函数关系用图象表示为( )
解析:由题意可知h=20-5t(0≤t≤4),所以其图象为B.故选B.
1
2
3
4
√
1
2
3
4
2.某单位为鼓励职工节约用水,作出如下规定:每位职工每月用水不超过10 m3的,按3元/m3收费;用水超过10 m3的,超过的部分按5元/m3收费.某职工某月缴水费55元,则该职工这个月实际用水为( )
A.13 m3 B.14 m3
C.15 m3 D.16 m3
√
1
2
3
4
1
2
3
4
√
1
2
3
4
4.已知某种食品的保鲜时间y(单位:h)与储藏温度x(单位:℃)之间满足函数关系y=a·2bx.若该食品在4 ℃时保鲜时间为192 h,在12 ℃时保鲜时间为48 h,则该食品在28 ℃时保鲜时间为( )
A.2 h B.3 h
C.4 h D.6 h
1
2
3
4
√
1
2
3
4
√
√
[例3] 一个车辆制造厂引进了一条摩托车整车装配流水线,这条流水线生产的摩托车数量x(辆)与创造的价值y
(元)之间满足二次函数关系.已知当产量为0时,创造的价值也为0;当产量为55辆时,创造的价值达到最大
6 050元.若这家工厂希望利用这条流水线创收达到
6 000元及以上,则它应该生产的摩托车数量至少是
.
50辆
解析:由题意,设摩托车数量x(辆)与创造的价值y(元)之间满足二次函数y=a(x-55)2+6 050(a<0),又当x=0时,y=0,所以a=-2,故y=-2x2+220x,则-2x2+220x≥
6 000,解得50≤x≤60.
(2)已知该地下车库的面积为2 560 m2,当积水深度小于等于
0.05 m时,小区居民方可入内,那么从消防部门开始排水时算起,至少需要经过几个小时以后,小区居民才能进入地下车库
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
