12.2 二次根式的乘除(第1课时)(同步课件)-八年级数学下册同步精品课堂(苏科版)
文档属性
| 名称 | 12.2 二次根式的乘除(第1课时)(同步课件)-八年级数学下册同步精品课堂(苏科版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-08 09:20:57 | ||
图片预览







文档简介
(共24张PPT)
第12章 · 二次根式
12.2 二次根式的乘除(1)
第1课时 二次根式的乘法
学习目标
1. 经历观察、比较的过程,理解二次根式的乘法法则,
并能运用二次根式的乘法法则进行计算;
2. 在理解二次根式乘法法则的基础上,会逆用该法则
化简二次根式.
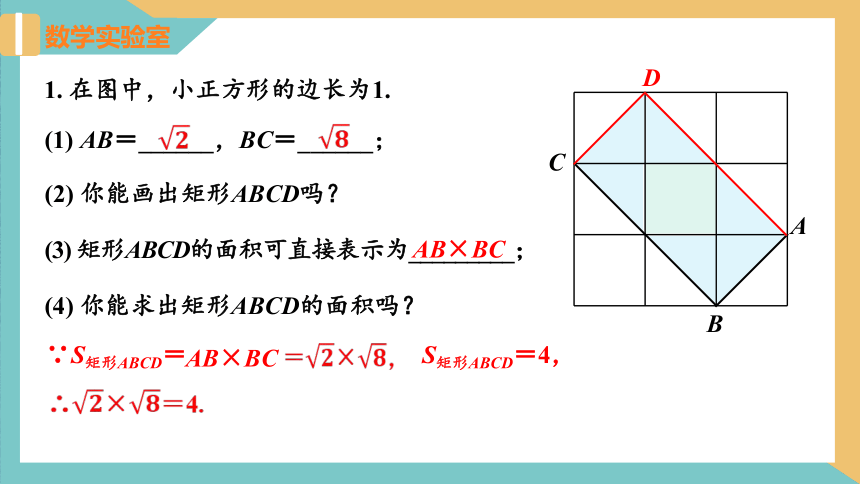
1. 在图中,小正方形的边长为1.
数学实验室
A
B
C
D
(1) AB=______,BC=______;
(2) 你能画出矩形ABCD吗?
(3) 矩形ABCD的面积可直接表示为_________;
AB×BC
(4) 你能求出矩形ABCD的面积吗?
∵S矩形ABCD=
AB×BC
=×,
S矩形ABCD=4,
∴×=4.
数学实验室
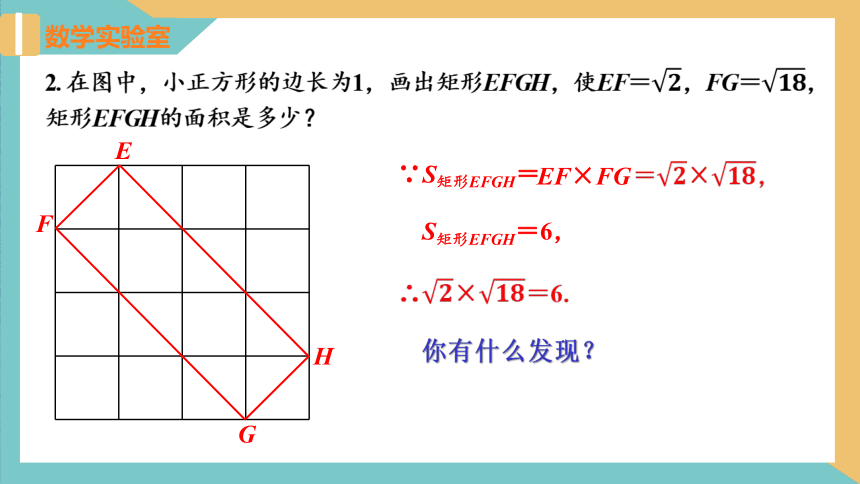
2. 在图中,小正方形的边长为1,画出矩形EFGH,使EF=,FG=,
矩形EFGH的面积是多少?
E
F
G
H
∵S矩形EFGH=
EF×FG
=×,
S矩形EFGH=6,
∴×=6.
你有什么发现?
尝试与交流
1.填空:
(1) ×=__________,=__________;
(2) ×=__________,=__________;
(3) ×=__________,=__________.
10
10
12
12
2. 比较上述各式,你有什么发现?请与同学交流.
3. ×与相等吗?
猜想与归纳
猜想:
= (a≥0,b≥0)
证明:
当a≥0、b≥0时,
=
由此可见,与都是ab的算术平方根.
所以,= .
新知归纳
二次根式乘法法则:
= (a≥0,b≥0)
算术平方根的积等于各个被开方数积的算术平方根.
文字语言叙述:
例题讲解
例1 计算:
(1) ×;
(2) ×;
(3) · (a≥0).
解:(1)×==;
(2)×==;
(3)当a≥0时,==4a.
新知巩固
1. 计算:
(1) ×;
(2) ×;
(3) ×.
解:(1)×==;
(2)×==;
(3)×==.
(1) · (a≥0);
新知巩固
2. 计算:
(2) ××;
(3) .
解:(1)当a≥0时,·==3;
推广:= (a≥0、b≥0、c≥0)
(2) ==30;
(3) ====.
新知探索
由= (a≥0,b≥0),
反过来得:
利用这个等式可以化简一些二次根式.
= (a≥0,b≥0)
例题讲解
例2 化简:
(1) ;
(2) (a≥0);
(3) (a≥0,b≥0).
解:(1)====2;
(2)当a≥0时,==·=;
(3)当a≥0、b≥0时,===·=.
二次根式运算的结果中,被开方数应不含能开得尽方的因数或因式.
新知巩固
3.化简:
(1) ;
(2) ;
(3) ;
解:(1)==4×5=20;
(2)====5;
(3)===;
新知巩固
3.化简:
(4) (a≥0,b≥0);
(5) .
(4)当a≥0、b≥0时,
=
=
=3ab;
(5)
=
=
=
=6×4
=24.
归纳总结
(3)如果因式中有平方式(或平方数),应用关系式=a(a≥0)把这个因式(或
因数)开出来,将二次根式化简.
化简二次根式的“三个步骤”:
(1)把被开方数分解因式(或因数);
(2)把各因式(或因数)积的算术平方根化为每个因式(或因数)的算术平方根的积;
解:∵=成立,
∴
解得-1≤x≤2.
例题讲解
要保证每个根式都有意义,须满足每个二次根式的被开方数都要有意义,据此列出不等式组,从而求出字母的取值范围.
例3 如果=成立,求x的取值范围.
新知巩固
1.等式成立的条件是 ( )
A. B. C.或 D.
A
2.如果,那么的取值范围是________.
课堂小结
12.2 二次根式的乘除(1)
乘法法则
(a≥0, b≥0)
法则逆用
=(a≥0, b≥0)
当堂检测
2.化简的结果是 ( )
A.2 B.2 C.-2 D.±2
B
1.计算×的结果等于 ( )
A.3 B.9 C.3 D.5
C
当堂检测
3.下列各式中,与的积为有理数的是 ( )
A. B. C. D.
A
4. 若=a,=b,则可以表示为( )
A. B. C.a2b D.ab
C
6. (1)如果=成立的条件是__________.
当堂检测
5.计算:×= ,= ;
3
(2)若=·,则x的取值范围是________.
x≥2
x≥1
18
当堂检测
7. 计算(a<0)的结果是__________.
-4a
8. 直角三角形的两条直角边长分别为cm,cm,则这个直角三角形的面积为________.
cm2
当堂检测
9. 计算:
(1)×; (2)××; (3)·(a≥0).
解:(1)×===6;
(3)当a≥0时,·===6a.
(2)×× ===30;
当堂检测
(1);(2);(3)(x≥0);(4)(a≥0,b≥0).
解:(1)==×=6.
(2)===7.
(3)==·=2x.
(4)==·=2a2b.
10. 化简:
第12章 · 二次根式
12.2 二次根式的乘除(1)
第1课时 二次根式的乘法
学习目标
1. 经历观察、比较的过程,理解二次根式的乘法法则,
并能运用二次根式的乘法法则进行计算;
2. 在理解二次根式乘法法则的基础上,会逆用该法则
化简二次根式.
1. 在图中,小正方形的边长为1.
数学实验室
A
B
C
D
(1) AB=______,BC=______;
(2) 你能画出矩形ABCD吗?
(3) 矩形ABCD的面积可直接表示为_________;
AB×BC
(4) 你能求出矩形ABCD的面积吗?
∵S矩形ABCD=
AB×BC
=×,
S矩形ABCD=4,
∴×=4.
数学实验室
2. 在图中,小正方形的边长为1,画出矩形EFGH,使EF=,FG=,
矩形EFGH的面积是多少?
E
F
G
H
∵S矩形EFGH=
EF×FG
=×,
S矩形EFGH=6,
∴×=6.
你有什么发现?
尝试与交流
1.填空:
(1) ×=__________,=__________;
(2) ×=__________,=__________;
(3) ×=__________,=__________.
10
10
12
12
2. 比较上述各式,你有什么发现?请与同学交流.
3. ×与相等吗?
猜想与归纳
猜想:
= (a≥0,b≥0)
证明:
当a≥0、b≥0时,
=
由此可见,与都是ab的算术平方根.
所以,= .
新知归纳
二次根式乘法法则:
= (a≥0,b≥0)
算术平方根的积等于各个被开方数积的算术平方根.
文字语言叙述:
例题讲解
例1 计算:
(1) ×;
(2) ×;
(3) · (a≥0).
解:(1)×==;
(2)×==;
(3)当a≥0时,==4a.
新知巩固
1. 计算:
(1) ×;
(2) ×;
(3) ×.
解:(1)×==;
(2)×==;
(3)×==.
(1) · (a≥0);
新知巩固
2. 计算:
(2) ××;
(3) .
解:(1)当a≥0时,·==3;
推广:= (a≥0、b≥0、c≥0)
(2) ==30;
(3) ====.
新知探索
由= (a≥0,b≥0),
反过来得:
利用这个等式可以化简一些二次根式.
= (a≥0,b≥0)
例题讲解
例2 化简:
(1) ;
(2) (a≥0);
(3) (a≥0,b≥0).
解:(1)====2;
(2)当a≥0时,==·=;
(3)当a≥0、b≥0时,===·=.
二次根式运算的结果中,被开方数应不含能开得尽方的因数或因式.
新知巩固
3.化简:
(1) ;
(2) ;
(3) ;
解:(1)==4×5=20;
(2)====5;
(3)===;
新知巩固
3.化简:
(4) (a≥0,b≥0);
(5) .
(4)当a≥0、b≥0时,
=
=
=3ab;
(5)
=
=
=
=6×4
=24.
归纳总结
(3)如果因式中有平方式(或平方数),应用关系式=a(a≥0)把这个因式(或
因数)开出来,将二次根式化简.
化简二次根式的“三个步骤”:
(1)把被开方数分解因式(或因数);
(2)把各因式(或因数)积的算术平方根化为每个因式(或因数)的算术平方根的积;
解:∵=成立,
∴
解得-1≤x≤2.
例题讲解
要保证每个根式都有意义,须满足每个二次根式的被开方数都要有意义,据此列出不等式组,从而求出字母的取值范围.
例3 如果=成立,求x的取值范围.
新知巩固
1.等式成立的条件是 ( )
A. B. C.或 D.
A
2.如果,那么的取值范围是________.
课堂小结
12.2 二次根式的乘除(1)
乘法法则
(a≥0, b≥0)
法则逆用
=(a≥0, b≥0)
当堂检测
2.化简的结果是 ( )
A.2 B.2 C.-2 D.±2
B
1.计算×的结果等于 ( )
A.3 B.9 C.3 D.5
C
当堂检测
3.下列各式中,与的积为有理数的是 ( )
A. B. C. D.
A
4. 若=a,=b,则可以表示为( )
A. B. C.a2b D.ab
C
6. (1)如果=成立的条件是__________.
当堂检测
5.计算:×= ,= ;
3
(2)若=·,则x的取值范围是________.
x≥2
x≥1
18
当堂检测
7. 计算(a<0)的结果是__________.
-4a
8. 直角三角形的两条直角边长分别为cm,cm,则这个直角三角形的面积为________.
cm2
当堂检测
9. 计算:
(1)×; (2)××; (3)·(a≥0).
解:(1)×===6;
(3)当a≥0时,·===6a.
(2)×× ===30;
当堂检测
(1);(2);(3)(x≥0);(4)(a≥0,b≥0).
解:(1)==×=6.
(2)===7.
(3)==·=2x.
(4)==·=2a2b.
10. 化简:
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
