初中数学人教版八年级下册18.2.1矩形-教学设计 (第2课时)(表格式)
文档属性
| 名称 | 初中数学人教版八年级下册18.2.1矩形-教学设计 (第2课时)(表格式) |

|
|
| 格式 | docx | ||
| 文件大小 | 252.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-06 00:00:00 | ||
图片预览

文档简介
教学设计
课程基本信息
课题 18.2.1 矩形(第二课时)
教学目标
1. 经历矩形判定定理的发现过程,掌握矩形的判定定理,能够运用判定定理解决有关问题。 2. 能够根据条件选择恰当的方法判定矩形,能够运用矩形的判定定理解释实际生活中的问题和现象。
教学内容
教学重点: 1. 掌握矩形的判定定理。
2. 运用矩形的判定定理解决有关问题。
教学难点: 判定定理“对角线相等的平行四边形是矩形”的发现和证明学生会出现困难,是本节教学的难点。
教学过程
一、新知导入 工人师傅在做门窗或矩形零件时,如何确保图形是矩形呢?现在师傅带了两种工具(卷尺和量角器),他说用这两种工具的任意一种就可以解决问题,这是为什么呢?
二、新知探究 性质:矩形的四个角都是直角; 矩形的对角线相等. 探究:逆命题是什么?成立吗?
猜想1 有三个角是直角的四边形是矩形.
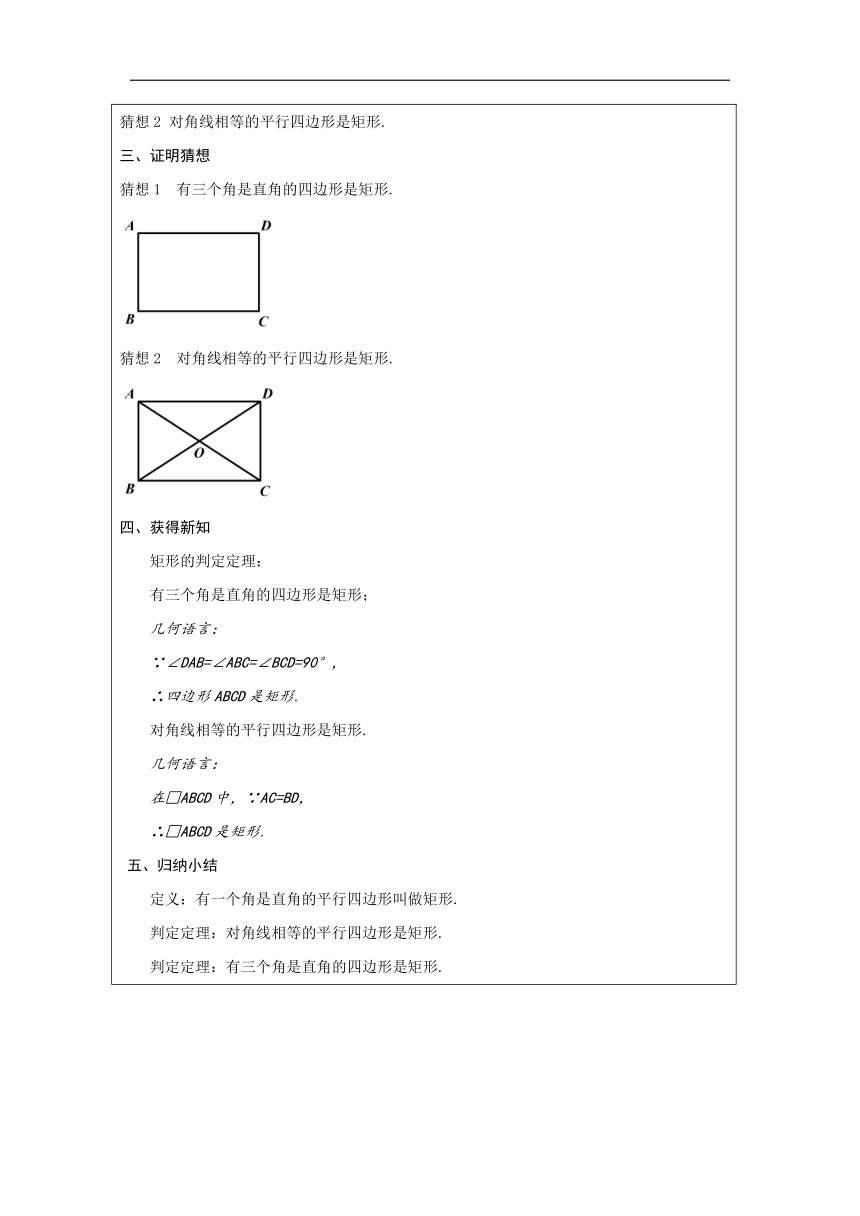
猜想2 对角线相等的平行四边形是矩形. 三、证明猜想 猜想1 有三个角是直角的四边形是矩形.
猜想2 对角线相等的平行四边形是矩形.
四、获得新知 矩形的判定定理: 有三个角是直角的四边形是矩形; 几何语言: ∵∠DAB=∠ABC=∠BCD=90°, ∴四边形ABCD是矩形. 对角线相等的平行四边形是矩形. 几何语言: 在□ABCD中,∵AC=BD, ∴□ABCD是矩形.
五、归纳小结
定义:有一个角是直角的平行四边形叫做矩形. 判定定理:对角线相等的平行四边形是矩形. 判定定理:有三个角是直角的四边形是矩形.
当堂检测 如图,在□ABCD中,对角线AC,BD相交于点O.下列条件不能判定□ABCD为矩形的是( ). A.AD=BC,AB∥CD B.AC=BD C.∠BAD=∠ADC D.∠ABC=90°
七、蓦然回首
现在你知道为什么师傅用两种工具(卷尺和量角器)的任意一种就可以确保图形是矩形了吗?
八、例题解析 例2 如图,在□ABCD中,对角线AC,BD相交于点O,且OA = OD,∠OAD = 50°.求∠OAB 的度数.
九、练习巩固 如图,□ABCD中的对角线AC,BD相交于点O,△OAB是等边三角形,且AB=4.求□ABCD 的面积.
十、课堂小结
课程基本信息
课题 18.2.1 矩形(第二课时)
教学目标
1. 经历矩形判定定理的发现过程,掌握矩形的判定定理,能够运用判定定理解决有关问题。 2. 能够根据条件选择恰当的方法判定矩形,能够运用矩形的判定定理解释实际生活中的问题和现象。
教学内容
教学重点: 1. 掌握矩形的判定定理。
2. 运用矩形的判定定理解决有关问题。
教学难点: 判定定理“对角线相等的平行四边形是矩形”的发现和证明学生会出现困难,是本节教学的难点。
教学过程
一、新知导入 工人师傅在做门窗或矩形零件时,如何确保图形是矩形呢?现在师傅带了两种工具(卷尺和量角器),他说用这两种工具的任意一种就可以解决问题,这是为什么呢?
二、新知探究 性质:矩形的四个角都是直角; 矩形的对角线相等. 探究:逆命题是什么?成立吗?
猜想1 有三个角是直角的四边形是矩形.
猜想2 对角线相等的平行四边形是矩形. 三、证明猜想 猜想1 有三个角是直角的四边形是矩形.
猜想2 对角线相等的平行四边形是矩形.
四、获得新知 矩形的判定定理: 有三个角是直角的四边形是矩形; 几何语言: ∵∠DAB=∠ABC=∠BCD=90°, ∴四边形ABCD是矩形. 对角线相等的平行四边形是矩形. 几何语言: 在□ABCD中,∵AC=BD, ∴□ABCD是矩形.
五、归纳小结
定义:有一个角是直角的平行四边形叫做矩形. 判定定理:对角线相等的平行四边形是矩形. 判定定理:有三个角是直角的四边形是矩形.
当堂检测 如图,在□ABCD中,对角线AC,BD相交于点O.下列条件不能判定□ABCD为矩形的是( ). A.AD=BC,AB∥CD B.AC=BD C.∠BAD=∠ADC D.∠ABC=90°
七、蓦然回首
现在你知道为什么师傅用两种工具(卷尺和量角器)的任意一种就可以确保图形是矩形了吗?
八、例题解析 例2 如图,在□ABCD中,对角线AC,BD相交于点O,且OA = OD,∠OAD = 50°.求∠OAB 的度数.
九、练习巩固 如图,□ABCD中的对角线AC,BD相交于点O,△OAB是等边三角形,且AB=4.求□ABCD 的面积.
十、课堂小结
