初中数学人教版八年级下册18.2.3正方形-教学设计(表格式)
文档属性
| 名称 | 初中数学人教版八年级下册18.2.3正方形-教学设计(表格式) |
|
|
| 格式 | docx | ||
| 文件大小 | 387.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-06 00:00:00 | ||
图片预览


文档简介
教学设计
课程基本信息
学科 初中数学 年级 八年级 学期 春季
课题 18.2.3正方形
教学目标
1.掌握正方形的概念。 2.掌握正方形的判定。 3.了解正方形与平行四边形、矩形、菱形的关系。 4.掌握正方形的性质定理:正方形的四个角是直角,四条边相等;正方形的对角线相等,并且互相垂直平分,每条对角线平分一组对角。 5.会用正方形的性质定理解决一些有关正方形的论证和计算等问题。
教学内容
教学重点: 正方形的判定和性质。
教学难点: 正方形的判定和性质归纳。 例2用到正方形的性质较多,如何选出有用的性质是证明的难点。
教学过程
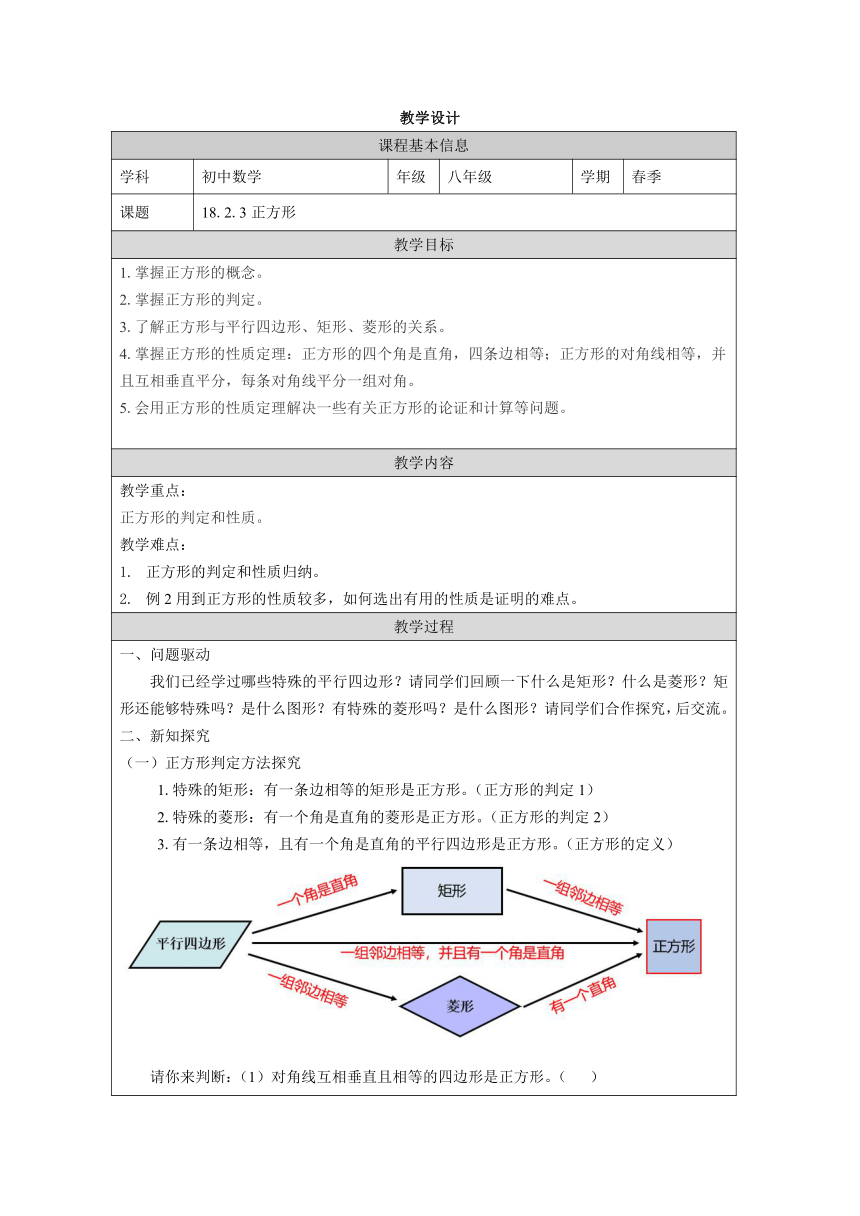
一、问题驱动 我们已经学过哪些特殊的平行四边形?请同学们回顾一下什么是矩形?什么是菱形?矩形还能够特殊吗?是什么图形?有特殊的菱形吗?是什么图形?请同学们合作探究,后交流。 二、新知探究 (一)正方形判定方法探究 1.特殊的矩形:有一条边相等的矩形是正方形。(正方形的判定1) 2.特殊的菱形:有一个角是直角的菱形是正方形。(正方形的判定2) 3.有一条边相等,且有一个角是直角的平行四边形是正方形。(正方形的定义) 请你来判断:(1)对角线互相垂直且相等的四边形是正方形。( ) (2)如果一个菱形的对角线相等,那么它一定是正方形。( ) (3)如果一个矩形的对角线互相垂直,那么它一定是正方形。( ) (4)四条边相等,且有一个角是直角的四边形是正方形。( ) (5)对角线互相垂直平分且相等的四边形是正方形。( ) 例题演练 例1 已知:如图,在Rt△ABC中,∠ACB=90°,CD是∠ACB的平分线, DE⊥BC,DF⊥AC,垂足分别是E,F . 求证:四边形CFDE是正方形. 思路分析1:矩形+一组邻边相等→正方形 思路分析2:菱形+一个直角→正方形 请同学们写出证明过程。 证明:∵DE⊥BE,DF⊥AC, ∴∠DEC=∠DFC=90°. 又∵∠ACB=90°, ∴四边形CFDE是矩形(有三个角是直角的四边形是矩形) 又∵CD是∠ACB的平分线, ∴DE=DF(角平分线上的点到角两边的距离相等) ∴四边形CFDE是正方形. (二)正方形的性质探究 正方形矩有哪些性质呢?请你把它们写下出来,并和同学们做一下交流,然后证明其中的一些结论。交流后师生归纳: 例题演练 新知应用 例2 求证:正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形。 已知:如图,四边形ABCD是正方形,对角线AC,BD相交于点O。 求证:△ABO,△BCO,△COD,△DOA是全等的等腰三角形。 证明:∵四边形ABCD是正方形, ∴AC⊥BD,AC=BD,AO=OC,BO=OD.(正方形的对角线相等,且互相垂直平分) ∴AO=OC=BO=OD, ∴ △ABO≌△BCO ≌ △COD ≌ △DOA(SAS),并且它们都是等腰直角三角形。 思考:图中共有多少个等腰直角三角形呢? 答:8个,分别是△ABO,△BCO, △COD,△DOA,△ADC,△DCB, △CBA,△BAD. (三)平行四边形、矩形、菱形、正方形的关系 思考:正方形、菱形、矩形、平行四边形之间有什么关系?与同学们讨论一下,并列表或用框图标表示这些关系。 三、应用新知,巩固练习 1.如图,ABCD是一块正方形场地,小华和小芳在AB边上取定了一点E,测量知,EC=30m,EB=10m,这块场地的面积和对角线长分别是多少? 解:∵∠B=Rt∠, ∴BC2+BE2=EC2, ∴BC2=EC2-BE2=302-102=800 ∴正方形ABCD的面积为800平方米。 ∵AC2=BC2+AB2=800+800=1600, ∴对角线AC=40m 2.已知,如图,在正方形ABCD中,G是对角线BD上的一点,GE⊥CD,GF⊥BC,E、F分别为垂足,连结AG,EF. 求证:AG=EF 证明:连结CG. 在△AGD和△CGD中, ∠ADG=∠CDG(正方形的对角线平分一组对角) DG=DG, AD=CD(正方形的四条边相等) ∴△AGD≌△CGD(SAS) ∴ AG=CG, ∵ GE⊥CD, GF⊥BC, ∴ ∠GFC= ∠GEC =90° 又∵ ∠BCD =90° ∴ 四边形FCEG是矩形(有三个角是直角的四边形是矩形) ∴ EF=CG(矩形的两条对角线相等) ∴ AG=EF 四、知识梳理 提高升华
课程基本信息
学科 初中数学 年级 八年级 学期 春季
课题 18.2.3正方形
教学目标
1.掌握正方形的概念。 2.掌握正方形的判定。 3.了解正方形与平行四边形、矩形、菱形的关系。 4.掌握正方形的性质定理:正方形的四个角是直角,四条边相等;正方形的对角线相等,并且互相垂直平分,每条对角线平分一组对角。 5.会用正方形的性质定理解决一些有关正方形的论证和计算等问题。
教学内容
教学重点: 正方形的判定和性质。
教学难点: 正方形的判定和性质归纳。 例2用到正方形的性质较多,如何选出有用的性质是证明的难点。
教学过程
一、问题驱动 我们已经学过哪些特殊的平行四边形?请同学们回顾一下什么是矩形?什么是菱形?矩形还能够特殊吗?是什么图形?有特殊的菱形吗?是什么图形?请同学们合作探究,后交流。 二、新知探究 (一)正方形判定方法探究 1.特殊的矩形:有一条边相等的矩形是正方形。(正方形的判定1) 2.特殊的菱形:有一个角是直角的菱形是正方形。(正方形的判定2) 3.有一条边相等,且有一个角是直角的平行四边形是正方形。(正方形的定义) 请你来判断:(1)对角线互相垂直且相等的四边形是正方形。( ) (2)如果一个菱形的对角线相等,那么它一定是正方形。( ) (3)如果一个矩形的对角线互相垂直,那么它一定是正方形。( ) (4)四条边相等,且有一个角是直角的四边形是正方形。( ) (5)对角线互相垂直平分且相等的四边形是正方形。( ) 例题演练 例1 已知:如图,在Rt△ABC中,∠ACB=90°,CD是∠ACB的平分线, DE⊥BC,DF⊥AC,垂足分别是E,F . 求证:四边形CFDE是正方形. 思路分析1:矩形+一组邻边相等→正方形 思路分析2:菱形+一个直角→正方形 请同学们写出证明过程。 证明:∵DE⊥BE,DF⊥AC, ∴∠DEC=∠DFC=90°. 又∵∠ACB=90°, ∴四边形CFDE是矩形(有三个角是直角的四边形是矩形) 又∵CD是∠ACB的平分线, ∴DE=DF(角平分线上的点到角两边的距离相等) ∴四边形CFDE是正方形. (二)正方形的性质探究 正方形矩有哪些性质呢?请你把它们写下出来,并和同学们做一下交流,然后证明其中的一些结论。交流后师生归纳: 例题演练 新知应用 例2 求证:正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形。 已知:如图,四边形ABCD是正方形,对角线AC,BD相交于点O。 求证:△ABO,△BCO,△COD,△DOA是全等的等腰三角形。 证明:∵四边形ABCD是正方形, ∴AC⊥BD,AC=BD,AO=OC,BO=OD.(正方形的对角线相等,且互相垂直平分) ∴AO=OC=BO=OD, ∴ △ABO≌△BCO ≌ △COD ≌ △DOA(SAS),并且它们都是等腰直角三角形。 思考:图中共有多少个等腰直角三角形呢? 答:8个,分别是△ABO,△BCO, △COD,△DOA,△ADC,△DCB, △CBA,△BAD. (三)平行四边形、矩形、菱形、正方形的关系 思考:正方形、菱形、矩形、平行四边形之间有什么关系?与同学们讨论一下,并列表或用框图标表示这些关系。 三、应用新知,巩固练习 1.如图,ABCD是一块正方形场地,小华和小芳在AB边上取定了一点E,测量知,EC=30m,EB=10m,这块场地的面积和对角线长分别是多少? 解:∵∠B=Rt∠, ∴BC2+BE2=EC2, ∴BC2=EC2-BE2=302-102=800 ∴正方形ABCD的面积为800平方米。 ∵AC2=BC2+AB2=800+800=1600, ∴对角线AC=40m 2.已知,如图,在正方形ABCD中,G是对角线BD上的一点,GE⊥CD,GF⊥BC,E、F分别为垂足,连结AG,EF. 求证:AG=EF 证明:连结CG. 在△AGD和△CGD中, ∠ADG=∠CDG(正方形的对角线平分一组对角) DG=DG, AD=CD(正方形的四条边相等) ∴△AGD≌△CGD(SAS) ∴ AG=CG, ∵ GE⊥CD, GF⊥BC, ∴ ∠GFC= ∠GEC =90° 又∵ ∠BCD =90° ∴ 四边形FCEG是矩形(有三个角是直角的四边形是矩形) ∴ EF=CG(矩形的两条对角线相等) ∴ AG=EF 四、知识梳理 提高升华
