期中备考:圆柱与圆锥(讲义)2023-2024学年数学六年级下册苏教版(含答案)
文档属性
| 名称 | 期中备考:圆柱与圆锥(讲义)2023-2024学年数学六年级下册苏教版(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 408.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-08 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
期中备考:圆柱与圆锥(讲义)2023-2024学年数学六年级下册苏教版
易错例题精讲一
.范华用硬纸板自制一个圆柱形笔筒,已知这个笔筒的底面半径是6厘米,高15厘米。如果不计损耗,做这个笔筒至少需要多少平方厘米的硬纸板?
【答案】678.24平方厘米
【分析】由于笔筒无盖,所以只求这个圆柱的侧面和一个底面的总面积,根据圆柱的侧面积公式:S=,圆的面积公式:S=,把数据代入公式解答。
【详解】2×3.14×6×15+3.14×62
=6.28×6×15+3.14×36
=565.2+113.04
=678.24(平方厘米)
答:做这个笔筒至少需要678.24平方厘米的硬纸板。
【点睛】此题主要考查圆柱表面积的应用。熟记并灵活运用圆柱的侧面积公式、圆的面积公式是解题的关键。
易错例题精讲二
.一个圆柱形玻璃容器里装有水,水中浸没着一个底面直径为12厘米,高为10厘米的圆锥形铁块,如果把它取出,那么容器中的水面高度将下降多少厘米?(圆柱形玻璃容器的底面内直径是15厘米)(得数保留一位小数)
【答案】2.1厘米
【分析】先根据V锥=πr2h,求出圆锥形铁块的体积;将圆锥形铁块从圆柱形容器的水中取出,水面会下降,水面下降部分的体积等于圆锥形铁块的体积;然后根据h=V÷S,用铁块的体积除以圆柱形容器的底面积,即可求出水面下降的高度。
【详解】圆锥形铁块的体积:
×3.14×(12÷2)2×10
=×3.14×36×10
=3.14×120
=376.8(立方厘米)
圆柱形容器的底面积:
3.14×(15÷2)2
=3.14×56.25
=176.625(平方厘米)
水面下降:
376.8÷176.625≈2.1(厘米)
答:容器中的水面高度将下降2.1厘米。
【点睛】本题考查圆柱、圆锥体积公式的灵活运用,抓住水下降部分的体积等于圆锥形铁块的体积,进而利用体积公式解答。
易错例题精讲三
.建筑工地有一个圆锥形的沙堆,底面积是50.24平方米,高是3米,用这堆沙在10米宽的公路上铺2厘米厚,能铺多少米长?
【答案】251.2米
【分析】根据圆锥的体积公式,先求出圆锥形沙堆的体积。由于沙子的体积不变,那么用沙子的体积除以公路的横截面面积,即可求出能铺多少米长。
【详解】×50.24×3=50.24(立方米)
2厘米=0.02米
50.24÷(10×0.02)
=50.24÷0.2
=251.2(米)
答:能铺251.2米长。
【点睛】本题考查了圆锥和长方体的体积,圆锥的体积=×底面积×高,长方体的体积=长×宽×高。
易错例题精讲四
.小明的妈妈榨了一些果汁,贮存在一个长方体容器中,果汁的高度为15厘米。小明将果汁往内直径6厘米、深10厘米的圆柱形玻璃杯中倒了满满一杯后,长方体容器中果汁的高度降至12厘米,这时长方体容器中的果汁大约还有多少升?(保留一位小数)
【答案】1.1升
【分析】根据圆柱的容积公式:V=πr2h,据此求出圆柱形玻璃杯中果汁的体积,此果汁的体积就是高为15-12=3厘米长方体的容积,然后根据长方体的容积公式:V=Sh求出长方体容器的底面积,进而求出此时长方体容器中剩下的果汁的升数。
【详解】3.14×(6÷2)2×10÷(15-12)
=3.14×9×10÷3
=282.6÷3
=94.2(平方厘米)
94.2×12=1130.4(立方厘米)=1.1304(立方分米)≈1.1(升)
答:这时长方体容器中的果汁大约还有1.1升。
【点睛】本题考查圆柱和长方体的容积,熟记公式是解题的关键。
精选好题练习
1.在长12厘米,宽10厘米,高8厘米的长方体中切出一个体积最大的圆柱,这个圆柱的体积是多少立方厘米?
2.两个等高的圆柱底面半径的比是4∶3,它们的体积比是多少?
3.把一个正方体木块加工成最大的圆锥体,它的底面半径是5厘米,这个正方体的体积是多少立方厘米?
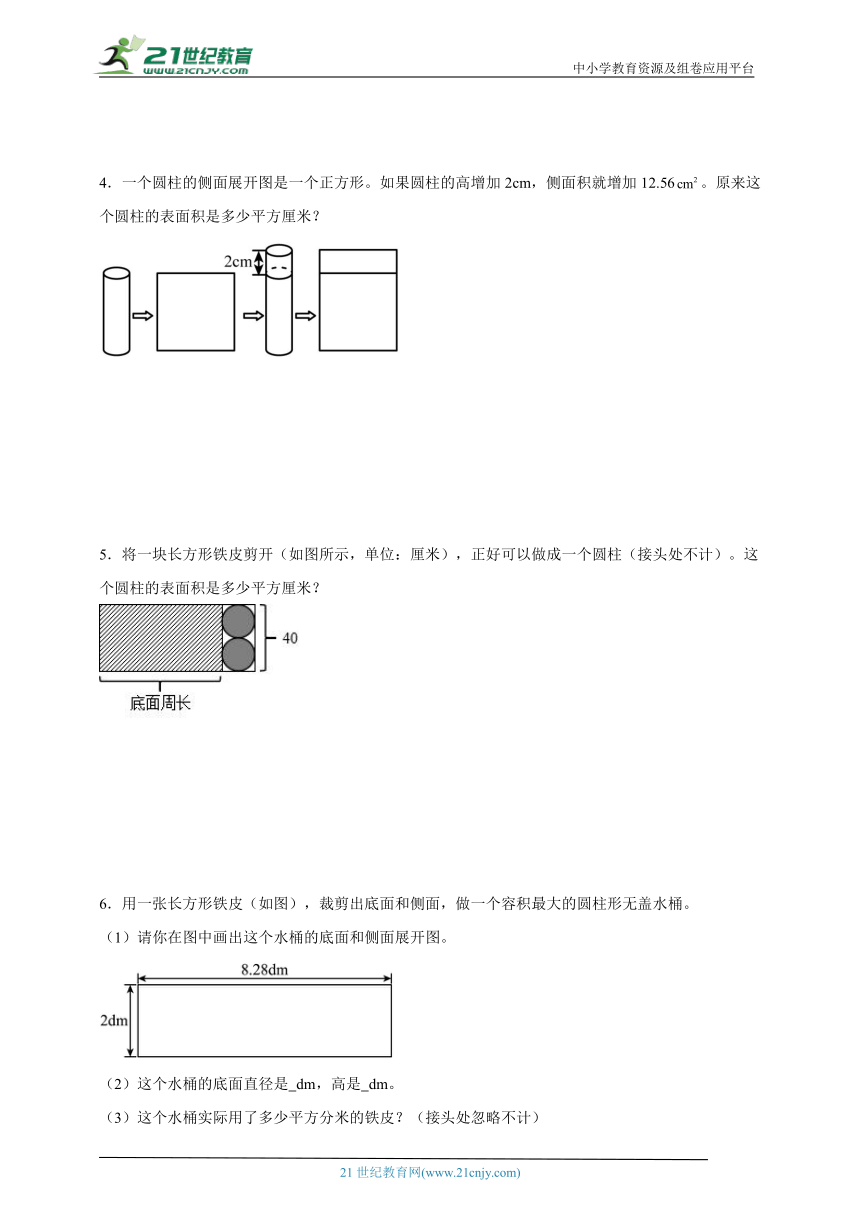
4.一个圆柱的侧面展开图是一个正方形。如果圆柱的高增加2cm,侧面积就增加12.56。原来这个圆柱的表面积是多少平方厘米?
5.将一块长方形铁皮剪开(如图所示,单位:厘米),正好可以做成一个圆柱(接头处不计)。这个圆柱的表面积是多少平方厘米?
6.用一张长方形铁皮(如图),裁剪出底面和侧面,做一个容积最大的圆柱形无盖水桶。
(1)请你在图中画出这个水桶的底面和侧面展开图。
(2)这个水桶的底面直径是 dm,高是 dm。
(3)这个水桶实际用了多少平方分米的铁皮?(接头处忽略不计)
(4)这个水桶最多能盛水多少升?(铁皮厚度忽略不计)
7.建筑工人使用一个圆锥形的铅锤来判断建筑物是否垂直,这个铅锤底面半径2cm,高6cm,每立方厘米铅锤约重7.8g,这个铅锤重多少g?
8.如图所示的百宝箱,上部是一个圆柱的一半,下部是一个长50cm,宽40cm,高20cm的长方体,这个百宝箱的表面积是多少?
9.如图是圆木沿某一平面截去一部分后的剩余部分,请计算剩余部分的体积。(单位:厘米)
10.一个底面半径是6cm的圆柱形玻璃器皿里装有一部分水,水中浸没着一个高9cm的圆锥形铅锤(水没有溢出)。当铅锤从水中取出后,水面下降了0.5cm。这个铅锤的底面积是多少平方厘米?
11.蒙古包也称“毡包”,是蒙古族传统民居,如图中的蒙古包是由一个圆柱体和一个圆锥体组成的(单位:米)。这个蒙古包占地面积是多少?内部的空间约是多少?(得数保留整数)
12.人们都习惯在口渴时才喝水。其实当大家感到口渴时,已经是身体需要水发出的信号,这表明此时身体已经脱水了。为此,这种口渴了才喝水的习惯不利于身体健康。所以平时要注意主动喝水,补充水分。营养学家建议:每日喝水应不少于1500毫升,淘气每天用从里面量底面直径为6厘米,高为10厘米的水杯,喝6满杯水。淘气每天的饮水量达到要求了吗?
13.王鹏爸爸在王鹏生日时订了一个蛋糕,蛋糕店阿姨用一个底面直径是40厘米,高10厘米的圆柱形蛋糕盒装这个蛋糕,用塑料绳捆扎蛋糕盒(如图),打结处正好是底面圆心,打结处用去绳子26厘米。
(1)蛋糕店阿姨扎这个蛋糕盒子至少需要多少厘米塑料绳?
(2)这个蛋糕盒的侧面积至少需要多少平方厘米?(接口处忽略不计)
(3)蛋糕盒的体积是多少立方厘米?合多少立方分米?
14.学校自来水管是圆柱形的,它内直径是2cm,水管内水流速度是每秒10cm。一个同学洗手时忘记关闭水龙头。10分钟后,王老师发现并关闭了水龙头。这时已经浪费多少L水?
参考答案:
1.628立方厘米
【分析】以长12厘米,宽10厘米作为底面,8厘米作为高。此时10厘米为圆柱底面直径,8厘米是圆柱的高。结合公式计算即可。
【详解】
=3.14×25×8
=78.5×8
=628(立方厘米)
答:这个圆柱体的体积是628立方厘米。
【点睛】本题考查圆柱的体积计算,以某个面为底面时,较小边就是底面圆的最大半径。
2.16∶9
【分析】圆柱体积=底面积×高,底面积=半径×半径×3.14。结合公式可以看出,高相等时,体积之比等于半径比的平方。
【详解】(4×4)∶(3×3)=16∶9
答:体积比是16∶9。
【点睛】本题考查不同圆柱的体积之比与底面半径之比以及高之比的关系。
3.1000立方厘米
【分析】由题干可知,把一个正方体木块加工成最大的圆锥体,圆锥体的底面直径等于正方体的棱长,再根据正方体的体积=棱长×棱长×棱长,即可解答。
【详解】由分析得,
5×2=10(厘米)
10×10×10
=100×10
=1000(立方厘米)
答:这个正方体的体积是1000立方厘米。
【点睛】此题考查的是立体图形的体积计算,解答此题要注意它们之间的内在联系。
4.45.7184平方厘米
【分析】观察图形可知,根据圆柱的侧面积=圆柱的底面周长×高,据此可求出圆柱的底面周长,进而求出圆柱的底面积,因为圆柱的侧面展开图是一个正方形,所以圆柱的高与圆柱的底面周长相等,然后根据圆柱的表面积=圆柱的侧面积+两个圆柱的底面积,据此解答即可。
【详解】12.56÷2=6.28(cm);
6.28×6.28+3.14×(6.28÷3.14÷2)2×2
=39.4384+3.14×1×2
=39.4384+6.28
=45.7184(平方厘米)
答:原来这个圆柱的表面积是45.7184平方厘米。
【点睛】本题考查圆柱的表面积,熟记公式是解题的关键。
5.3140平方厘米
【分析】由图可知:该圆柱的侧面是长为3.14×20=62.8厘米,高为40厘米的长方形;底面是直径为20厘米的圆;根据“圆的表面积=圆柱的侧面积+底面积×2”代入数值解答即可。
【详解】40÷2=20(厘米)
20÷2=10(厘米)
3.14×102×2+3.14×20×40
=3.14×100×2+3.14×20×40
=314×2+62.8×40
=628+2512
=3140(平方厘米)
答:这个圆柱的表面积是3140平方厘米。
【点睛】解答此题应明确:圆柱是由一个侧面和两个底面组成;进而根据圆柱表面积计算方法进行解答即可。
6.(1)见详解
(2)2;2
(3)15.7平方分米
(4)6.28升
【分析】(1)由长方形围成圆柱体积最大的原理可知这张铁皮以长为底面周长、以宽为高时围成的圆柱容积最大。根据圆柱侧面展开图的特征,圆柱的侧面沿高展开是一个长方形,这个长方形的长等于圆柱的底面周长,宽等于圆柱的高。通过观察图形可知,这个圆柱形水桶的底面直径是2分米,根据圆的画法,画出直径是2分米的圆,铁皮的长减去2分米就是圆柱的底面周长。据此作图即可。
(2)这个水桶的底面直径和高都是2分米。
(3)根据圆柱的侧面积公式:S=πdh,圆的面积公式:S=πr2,把数据代入公式解答。
(4)根据圆柱的体积(容积)公式:V=πr2h,把数据代入公式解答。
【详解】(1)作图如下:
(2)这个水桶的底面直径是2分米,高是2分米。
(3)8.28-2=6.28(分米)
6.28×2+3.14×(2÷2)2
=12.56+3.14×1
=12.56+3.14
=15.7(平方分米)
答:这个水桶实际用了15.7平方分米的铁皮。
(4)3.14×(2÷2)2×2
=3.14×1×2
=6.28(立方分米)
6.28立方分米=6.28升
答:这个水桶最多能盛水6.28升。
【点睛】面积相等的长方形,围成的圆柱体积是不同的,卷成圆柱的底面周长的那条边越长,围成的圆柱的体积越大。再结合这张长方形铁皮能够围成的圆柱的两种形状:①以宽为底面周长、以长为高围成一个圆柱;②以长为底面周长、以宽为高围成一个圆柱;接着确定能围成的容积最大的圆柱的方法是②;然后再展开相关计算。
7.195.936g
【分析】根据圆锥体积公式V=Sh,求出铅锤体积,用体积×每立方厘米重量=铅锤总重量。
【详解】×3.14×2 ×6×7.8
=25.12×7.8
=195.936(克)
答:这个铅锤重195.936g。
【点睛】本题主要考查了圆锥体积,圆锥体积=×底面积×高。
8.9996平方厘米
【分析】这个图形的表面积包含了圆柱的半个侧面积,以及一个底面积,同时还要加上长方体前面、后面、左面、右面和下面5个面的面积。
【详解】50×40+50×20×2+40×20×2+3.14×(40÷2)+3.14×40×50÷2
=2000+2000+1600+3.14×400+125.6×50÷2
=4000+1600+1256+6280÷2
=6856+3140
=9996(平方厘米)
答:百宝箱的表面积是9996平方厘米。
【点睛】本题考查组合图形的表面积,找准表面积是由哪些部分组成的是解题关键。
9.395.64立方厘米
【分析】根据图形的特点,可以这样理解,用这样两个完全一样的图形拼成一个高是(13+15)厘米的圆柱,根据圆柱的体积公式:V=sh,把数据代入公式求出这样两个图形的体积再除以2即可。
【详解】3.14×(6÷2)2×(13+15)÷2
=3.14×9×28÷2
=28.26×28÷2
=791.28÷2
=395.64(立方厘米)
答:这个立体图形的体积是395.64立方厘米。
【点睛】本题考查立体图形的切拼以及圆柱的体积计算。
10.18.84平方厘米
【分析】根据题意可知,当把圆锥从圆柱形容器中取出后,下降部分水的体积就等于这个圆锥的体积,根据圆柱的体积公式:V=πr2h,把数据代入公式取出这个圆锥的体积,再根据圆锥的体积公式:V=Sh,那么S=V÷÷h,把数据代入公式解答。
【详解】3.14×62×0.5÷÷9
=3.14×36×0.5×3÷9
=113.04×0.5×3÷9
=56.52×3÷9
=169.56÷9
=18.84(平方厘米)
答:这个铅锤的底面积是18.84平方厘米。
【点睛】此题主要考查圆柱、圆锥体积公式的灵活运用,关键是明白:当把圆锥从圆柱形容器中取出后,下降部分水的体积就等于这个圆锥的体积。
11.28.26平方米;66立方米
【分析】根据圆的面积公式:,求出它的占地面积,根据圆柱的体积(容积)公式:,圆锥的体积(容积)公式:,把数据代入公式求出内部的空间。
【详解】
(平方米)
×3.14×(6÷2) ×1+3.14×(6÷2) ×2
=9.42+56.52
(立方米)
(立方米)
答:这个蒙古包占地面积是28.26平方米,内部的空间约是66立方米。
【点睛】此题主要考查圆的面积公式、圆锥、圆柱的体积公式的灵活运用,关键是熟记公式。
12.达到要求
【分析】先根据圆柱的体积公式求出一杯水的体积,再求6杯水的体积,最后育与1500毫升比较即可。
【详解】6÷2=3(厘米)
3.14×32×10×6
=1695.6(立方厘米)
1695.6>1500
答:达到要求。
【点睛】本题考查圆柱的体积,解答本题的关键是掌握圆柱的体积计算公式。
13.(1)226厘米
(2)1256平方厘米
(3)12560立方厘米;12.56立方分米
【分析】(1)从图中可以看出,40厘米用了4条,10厘米用了4条,再加上打结处用去绳子26厘米,就是扎这个蛋糕盒子至少需要的塑料绳长度。
(2)根据圆柱的侧面积公式:S侧=πdh,代入数据计算即可。
(3)根据圆柱的体积公式:V=πr2h,代入数据计算,求出蛋糕盒的体积。注意单位的换算:1立方分米=1000立方厘米。
【详解】(1)40×4+10×4+26
=160+40+26
=200+26
=226(厘米)
答:扎这个蛋糕盒子至少需要226厘米塑料绳。
(2)3.14×40×10
=125.6×10
=1256(平方厘米)
答:这个蛋糕盒的侧面积至少需要1256平方厘米。
(3)3.14×(40÷2)2×10
=3.14×400×10
=1256×10
=12560(立方厘米)
12560立方厘米=12.56立方分米
答:蛋糕盒的体积是12560立方厘米,合12.56立方分米。
【点睛】掌握圆柱的特征、圆柱的侧面积公式、圆柱的体积公式是解题的关键。
14.18.84L
【分析】因为自来水管的内直径是2cm,所以半径是1cm,根据圆的面积公式:S=πr2,据此可求出圆柱的底面积,根据速度×时间=路程,可求出水流的距离也就是水的高度,然后根据圆柱的体积公式:V=Sh,即可求出浪费的水的体积。
【详解】10分钟=600秒
3.14×(2÷2)2×10×600
=3.14×10×600
=31.4×600
=18840(cm3)
=18.84(L)
答:这时已经浪费18.84L的水。
【点睛】本题考查圆柱的体积,明确水流的距离即可水流的高度是解题的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期中备考:圆柱与圆锥(讲义)2023-2024学年数学六年级下册苏教版
易错例题精讲一
.范华用硬纸板自制一个圆柱形笔筒,已知这个笔筒的底面半径是6厘米,高15厘米。如果不计损耗,做这个笔筒至少需要多少平方厘米的硬纸板?
【答案】678.24平方厘米
【分析】由于笔筒无盖,所以只求这个圆柱的侧面和一个底面的总面积,根据圆柱的侧面积公式:S=,圆的面积公式:S=,把数据代入公式解答。
【详解】2×3.14×6×15+3.14×62
=6.28×6×15+3.14×36
=565.2+113.04
=678.24(平方厘米)
答:做这个笔筒至少需要678.24平方厘米的硬纸板。
【点睛】此题主要考查圆柱表面积的应用。熟记并灵活运用圆柱的侧面积公式、圆的面积公式是解题的关键。
易错例题精讲二
.一个圆柱形玻璃容器里装有水,水中浸没着一个底面直径为12厘米,高为10厘米的圆锥形铁块,如果把它取出,那么容器中的水面高度将下降多少厘米?(圆柱形玻璃容器的底面内直径是15厘米)(得数保留一位小数)
【答案】2.1厘米
【分析】先根据V锥=πr2h,求出圆锥形铁块的体积;将圆锥形铁块从圆柱形容器的水中取出,水面会下降,水面下降部分的体积等于圆锥形铁块的体积;然后根据h=V÷S,用铁块的体积除以圆柱形容器的底面积,即可求出水面下降的高度。
【详解】圆锥形铁块的体积:
×3.14×(12÷2)2×10
=×3.14×36×10
=3.14×120
=376.8(立方厘米)
圆柱形容器的底面积:
3.14×(15÷2)2
=3.14×56.25
=176.625(平方厘米)
水面下降:
376.8÷176.625≈2.1(厘米)
答:容器中的水面高度将下降2.1厘米。
【点睛】本题考查圆柱、圆锥体积公式的灵活运用,抓住水下降部分的体积等于圆锥形铁块的体积,进而利用体积公式解答。
易错例题精讲三
.建筑工地有一个圆锥形的沙堆,底面积是50.24平方米,高是3米,用这堆沙在10米宽的公路上铺2厘米厚,能铺多少米长?
【答案】251.2米
【分析】根据圆锥的体积公式,先求出圆锥形沙堆的体积。由于沙子的体积不变,那么用沙子的体积除以公路的横截面面积,即可求出能铺多少米长。
【详解】×50.24×3=50.24(立方米)
2厘米=0.02米
50.24÷(10×0.02)
=50.24÷0.2
=251.2(米)
答:能铺251.2米长。
【点睛】本题考查了圆锥和长方体的体积,圆锥的体积=×底面积×高,长方体的体积=长×宽×高。
易错例题精讲四
.小明的妈妈榨了一些果汁,贮存在一个长方体容器中,果汁的高度为15厘米。小明将果汁往内直径6厘米、深10厘米的圆柱形玻璃杯中倒了满满一杯后,长方体容器中果汁的高度降至12厘米,这时长方体容器中的果汁大约还有多少升?(保留一位小数)
【答案】1.1升
【分析】根据圆柱的容积公式:V=πr2h,据此求出圆柱形玻璃杯中果汁的体积,此果汁的体积就是高为15-12=3厘米长方体的容积,然后根据长方体的容积公式:V=Sh求出长方体容器的底面积,进而求出此时长方体容器中剩下的果汁的升数。
【详解】3.14×(6÷2)2×10÷(15-12)
=3.14×9×10÷3
=282.6÷3
=94.2(平方厘米)
94.2×12=1130.4(立方厘米)=1.1304(立方分米)≈1.1(升)
答:这时长方体容器中的果汁大约还有1.1升。
【点睛】本题考查圆柱和长方体的容积,熟记公式是解题的关键。
精选好题练习
1.在长12厘米,宽10厘米,高8厘米的长方体中切出一个体积最大的圆柱,这个圆柱的体积是多少立方厘米?
2.两个等高的圆柱底面半径的比是4∶3,它们的体积比是多少?
3.把一个正方体木块加工成最大的圆锥体,它的底面半径是5厘米,这个正方体的体积是多少立方厘米?
4.一个圆柱的侧面展开图是一个正方形。如果圆柱的高增加2cm,侧面积就增加12.56。原来这个圆柱的表面积是多少平方厘米?
5.将一块长方形铁皮剪开(如图所示,单位:厘米),正好可以做成一个圆柱(接头处不计)。这个圆柱的表面积是多少平方厘米?
6.用一张长方形铁皮(如图),裁剪出底面和侧面,做一个容积最大的圆柱形无盖水桶。
(1)请你在图中画出这个水桶的底面和侧面展开图。
(2)这个水桶的底面直径是 dm,高是 dm。
(3)这个水桶实际用了多少平方分米的铁皮?(接头处忽略不计)
(4)这个水桶最多能盛水多少升?(铁皮厚度忽略不计)
7.建筑工人使用一个圆锥形的铅锤来判断建筑物是否垂直,这个铅锤底面半径2cm,高6cm,每立方厘米铅锤约重7.8g,这个铅锤重多少g?
8.如图所示的百宝箱,上部是一个圆柱的一半,下部是一个长50cm,宽40cm,高20cm的长方体,这个百宝箱的表面积是多少?
9.如图是圆木沿某一平面截去一部分后的剩余部分,请计算剩余部分的体积。(单位:厘米)
10.一个底面半径是6cm的圆柱形玻璃器皿里装有一部分水,水中浸没着一个高9cm的圆锥形铅锤(水没有溢出)。当铅锤从水中取出后,水面下降了0.5cm。这个铅锤的底面积是多少平方厘米?
11.蒙古包也称“毡包”,是蒙古族传统民居,如图中的蒙古包是由一个圆柱体和一个圆锥体组成的(单位:米)。这个蒙古包占地面积是多少?内部的空间约是多少?(得数保留整数)
12.人们都习惯在口渴时才喝水。其实当大家感到口渴时,已经是身体需要水发出的信号,这表明此时身体已经脱水了。为此,这种口渴了才喝水的习惯不利于身体健康。所以平时要注意主动喝水,补充水分。营养学家建议:每日喝水应不少于1500毫升,淘气每天用从里面量底面直径为6厘米,高为10厘米的水杯,喝6满杯水。淘气每天的饮水量达到要求了吗?
13.王鹏爸爸在王鹏生日时订了一个蛋糕,蛋糕店阿姨用一个底面直径是40厘米,高10厘米的圆柱形蛋糕盒装这个蛋糕,用塑料绳捆扎蛋糕盒(如图),打结处正好是底面圆心,打结处用去绳子26厘米。
(1)蛋糕店阿姨扎这个蛋糕盒子至少需要多少厘米塑料绳?
(2)这个蛋糕盒的侧面积至少需要多少平方厘米?(接口处忽略不计)
(3)蛋糕盒的体积是多少立方厘米?合多少立方分米?
14.学校自来水管是圆柱形的,它内直径是2cm,水管内水流速度是每秒10cm。一个同学洗手时忘记关闭水龙头。10分钟后,王老师发现并关闭了水龙头。这时已经浪费多少L水?
参考答案:
1.628立方厘米
【分析】以长12厘米,宽10厘米作为底面,8厘米作为高。此时10厘米为圆柱底面直径,8厘米是圆柱的高。结合公式计算即可。
【详解】
=3.14×25×8
=78.5×8
=628(立方厘米)
答:这个圆柱体的体积是628立方厘米。
【点睛】本题考查圆柱的体积计算,以某个面为底面时,较小边就是底面圆的最大半径。
2.16∶9
【分析】圆柱体积=底面积×高,底面积=半径×半径×3.14。结合公式可以看出,高相等时,体积之比等于半径比的平方。
【详解】(4×4)∶(3×3)=16∶9
答:体积比是16∶9。
【点睛】本题考查不同圆柱的体积之比与底面半径之比以及高之比的关系。
3.1000立方厘米
【分析】由题干可知,把一个正方体木块加工成最大的圆锥体,圆锥体的底面直径等于正方体的棱长,再根据正方体的体积=棱长×棱长×棱长,即可解答。
【详解】由分析得,
5×2=10(厘米)
10×10×10
=100×10
=1000(立方厘米)
答:这个正方体的体积是1000立方厘米。
【点睛】此题考查的是立体图形的体积计算,解答此题要注意它们之间的内在联系。
4.45.7184平方厘米
【分析】观察图形可知,根据圆柱的侧面积=圆柱的底面周长×高,据此可求出圆柱的底面周长,进而求出圆柱的底面积,因为圆柱的侧面展开图是一个正方形,所以圆柱的高与圆柱的底面周长相等,然后根据圆柱的表面积=圆柱的侧面积+两个圆柱的底面积,据此解答即可。
【详解】12.56÷2=6.28(cm);
6.28×6.28+3.14×(6.28÷3.14÷2)2×2
=39.4384+3.14×1×2
=39.4384+6.28
=45.7184(平方厘米)
答:原来这个圆柱的表面积是45.7184平方厘米。
【点睛】本题考查圆柱的表面积,熟记公式是解题的关键。
5.3140平方厘米
【分析】由图可知:该圆柱的侧面是长为3.14×20=62.8厘米,高为40厘米的长方形;底面是直径为20厘米的圆;根据“圆的表面积=圆柱的侧面积+底面积×2”代入数值解答即可。
【详解】40÷2=20(厘米)
20÷2=10(厘米)
3.14×102×2+3.14×20×40
=3.14×100×2+3.14×20×40
=314×2+62.8×40
=628+2512
=3140(平方厘米)
答:这个圆柱的表面积是3140平方厘米。
【点睛】解答此题应明确:圆柱是由一个侧面和两个底面组成;进而根据圆柱表面积计算方法进行解答即可。
6.(1)见详解
(2)2;2
(3)15.7平方分米
(4)6.28升
【分析】(1)由长方形围成圆柱体积最大的原理可知这张铁皮以长为底面周长、以宽为高时围成的圆柱容积最大。根据圆柱侧面展开图的特征,圆柱的侧面沿高展开是一个长方形,这个长方形的长等于圆柱的底面周长,宽等于圆柱的高。通过观察图形可知,这个圆柱形水桶的底面直径是2分米,根据圆的画法,画出直径是2分米的圆,铁皮的长减去2分米就是圆柱的底面周长。据此作图即可。
(2)这个水桶的底面直径和高都是2分米。
(3)根据圆柱的侧面积公式:S=πdh,圆的面积公式:S=πr2,把数据代入公式解答。
(4)根据圆柱的体积(容积)公式:V=πr2h,把数据代入公式解答。
【详解】(1)作图如下:
(2)这个水桶的底面直径是2分米,高是2分米。
(3)8.28-2=6.28(分米)
6.28×2+3.14×(2÷2)2
=12.56+3.14×1
=12.56+3.14
=15.7(平方分米)
答:这个水桶实际用了15.7平方分米的铁皮。
(4)3.14×(2÷2)2×2
=3.14×1×2
=6.28(立方分米)
6.28立方分米=6.28升
答:这个水桶最多能盛水6.28升。
【点睛】面积相等的长方形,围成的圆柱体积是不同的,卷成圆柱的底面周长的那条边越长,围成的圆柱的体积越大。再结合这张长方形铁皮能够围成的圆柱的两种形状:①以宽为底面周长、以长为高围成一个圆柱;②以长为底面周长、以宽为高围成一个圆柱;接着确定能围成的容积最大的圆柱的方法是②;然后再展开相关计算。
7.195.936g
【分析】根据圆锥体积公式V=Sh,求出铅锤体积,用体积×每立方厘米重量=铅锤总重量。
【详解】×3.14×2 ×6×7.8
=25.12×7.8
=195.936(克)
答:这个铅锤重195.936g。
【点睛】本题主要考查了圆锥体积,圆锥体积=×底面积×高。
8.9996平方厘米
【分析】这个图形的表面积包含了圆柱的半个侧面积,以及一个底面积,同时还要加上长方体前面、后面、左面、右面和下面5个面的面积。
【详解】50×40+50×20×2+40×20×2+3.14×(40÷2)+3.14×40×50÷2
=2000+2000+1600+3.14×400+125.6×50÷2
=4000+1600+1256+6280÷2
=6856+3140
=9996(平方厘米)
答:百宝箱的表面积是9996平方厘米。
【点睛】本题考查组合图形的表面积,找准表面积是由哪些部分组成的是解题关键。
9.395.64立方厘米
【分析】根据图形的特点,可以这样理解,用这样两个完全一样的图形拼成一个高是(13+15)厘米的圆柱,根据圆柱的体积公式:V=sh,把数据代入公式求出这样两个图形的体积再除以2即可。
【详解】3.14×(6÷2)2×(13+15)÷2
=3.14×9×28÷2
=28.26×28÷2
=791.28÷2
=395.64(立方厘米)
答:这个立体图形的体积是395.64立方厘米。
【点睛】本题考查立体图形的切拼以及圆柱的体积计算。
10.18.84平方厘米
【分析】根据题意可知,当把圆锥从圆柱形容器中取出后,下降部分水的体积就等于这个圆锥的体积,根据圆柱的体积公式:V=πr2h,把数据代入公式取出这个圆锥的体积,再根据圆锥的体积公式:V=Sh,那么S=V÷÷h,把数据代入公式解答。
【详解】3.14×62×0.5÷÷9
=3.14×36×0.5×3÷9
=113.04×0.5×3÷9
=56.52×3÷9
=169.56÷9
=18.84(平方厘米)
答:这个铅锤的底面积是18.84平方厘米。
【点睛】此题主要考查圆柱、圆锥体积公式的灵活运用,关键是明白:当把圆锥从圆柱形容器中取出后,下降部分水的体积就等于这个圆锥的体积。
11.28.26平方米;66立方米
【分析】根据圆的面积公式:,求出它的占地面积,根据圆柱的体积(容积)公式:,圆锥的体积(容积)公式:,把数据代入公式求出内部的空间。
【详解】
(平方米)
×3.14×(6÷2) ×1+3.14×(6÷2) ×2
=9.42+56.52
(立方米)
(立方米)
答:这个蒙古包占地面积是28.26平方米,内部的空间约是66立方米。
【点睛】此题主要考查圆的面积公式、圆锥、圆柱的体积公式的灵活运用,关键是熟记公式。
12.达到要求
【分析】先根据圆柱的体积公式求出一杯水的体积,再求6杯水的体积,最后育与1500毫升比较即可。
【详解】6÷2=3(厘米)
3.14×32×10×6
=1695.6(立方厘米)
1695.6>1500
答:达到要求。
【点睛】本题考查圆柱的体积,解答本题的关键是掌握圆柱的体积计算公式。
13.(1)226厘米
(2)1256平方厘米
(3)12560立方厘米;12.56立方分米
【分析】(1)从图中可以看出,40厘米用了4条,10厘米用了4条,再加上打结处用去绳子26厘米,就是扎这个蛋糕盒子至少需要的塑料绳长度。
(2)根据圆柱的侧面积公式:S侧=πdh,代入数据计算即可。
(3)根据圆柱的体积公式:V=πr2h,代入数据计算,求出蛋糕盒的体积。注意单位的换算:1立方分米=1000立方厘米。
【详解】(1)40×4+10×4+26
=160+40+26
=200+26
=226(厘米)
答:扎这个蛋糕盒子至少需要226厘米塑料绳。
(2)3.14×40×10
=125.6×10
=1256(平方厘米)
答:这个蛋糕盒的侧面积至少需要1256平方厘米。
(3)3.14×(40÷2)2×10
=3.14×400×10
=1256×10
=12560(立方厘米)
12560立方厘米=12.56立方分米
答:蛋糕盒的体积是12560立方厘米,合12.56立方分米。
【点睛】掌握圆柱的特征、圆柱的侧面积公式、圆柱的体积公式是解题的关键。
14.18.84L
【分析】因为自来水管的内直径是2cm,所以半径是1cm,根据圆的面积公式:S=πr2,据此可求出圆柱的底面积,根据速度×时间=路程,可求出水流的距离也就是水的高度,然后根据圆柱的体积公式:V=Sh,即可求出浪费的水的体积。
【详解】10分钟=600秒
3.14×(2÷2)2×10×600
=3.14×10×600
=31.4×600
=18840(cm3)
=18.84(L)
答:这时已经浪费18.84L的水。
【点睛】本题考查圆柱的体积,明确水流的距离即可水流的高度是解题的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
