人教版六年级下册数学 数的认识 (课件)(共79张PPT)
文档属性
| 名称 | 人教版六年级下册数学 数的认识 (课件)(共79张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-06 00:00:00 | ||
图片预览








文档简介
(共79张PPT)
6 整理和复习
1.数与代数
数学人教版六年级下册
第1课时 数的认识(一)
情境导入
你学过哪些数?它们在生活中有哪些应用?阅读下面的资料,你能发现什么?
第24届冬季奥林匹克运动会于2022年2月4日至2月20日在北京和河北张家口举行。
教材第71页
来自91个国家和地区的代表团总计2880名运动员参加了7个大项(包括15个分项、109个小项)的比赛。中国代表团共有176名运动员参加了比赛,其中女运动员87人,占49.43%;男运动员89人,占50.57%;运动员平均年龄25.2岁。中国代表团获得了9枚金牌、4枚银牌和2枚铜牌,列金牌榜第三位,金牌数和奖牌数均创历史新高。共有1.9万名志愿者参加了志愿服务。本届冬奥会践行“绿色办奥”的理念,实现了低碳、节能、环保的目标。本届冬奥会的主火炬采用“微火”技术,其碳排放量大约只有传统点火方式的;国家速滑馆“冰丝带”采用二氧化碳制冷技术,碳排放量约是传统制冰技术的。设计团队开发的智慧场馆系统,能将“冰丝带” 的冰面温度精确地维持在-11~-10 ℃。
小数
分数
负数
整数
百分数
归纳整理
教材第72页第1题
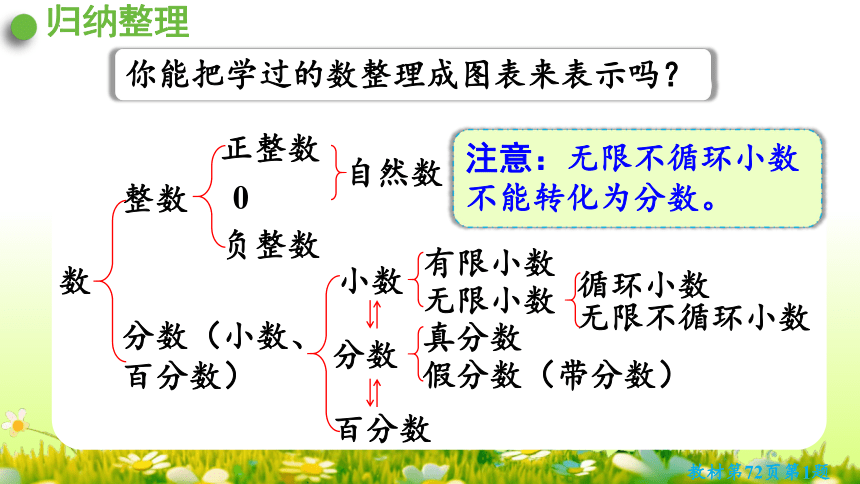
你能把学过的数整理成图表来表示吗?
数
整数
分数(小数、
百分数)
正整数
0
负整数
自然数
小数
分数
百分数
有限小数
无限小数
循环小数
无限不循环小数
真分数
假分数(带分数)
注意:无限不循环小数不能转化为分数。
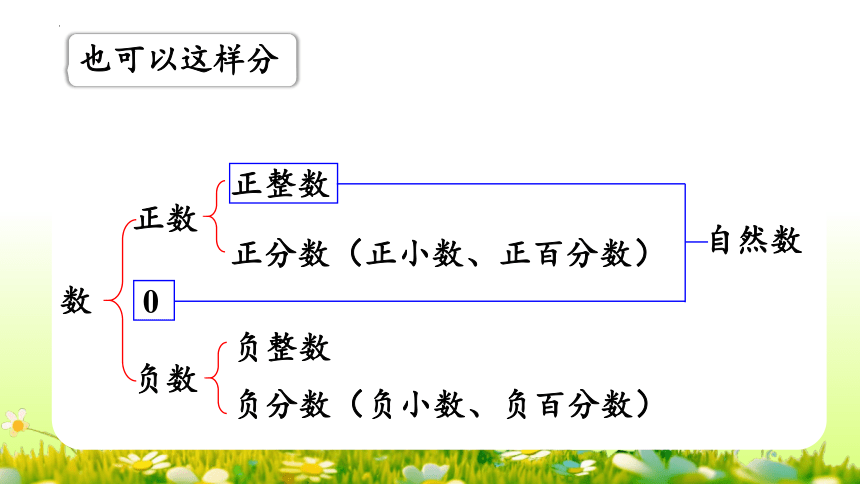
也可以这样分
数
正数
负数
正整数
0
正分数(正小数、正百分数)
自然数
负整数
负分数(负小数、负百分数)
整数
正整数
0
负整数
像1,2,3,…这样的数叫作正整数。
像-1,-2,-3,…这样的数叫作负整数。
整数
正整数的个数是无限的,最小的正整数是1,没有最大的正整数。
负整数的个数是无限的,最大的负整数是-1,没有最小的负整数。
像…,-3,-2,-1,0,1,2,3,…
这样的数统称为整数。
整数的个数是无限的,没有最小的整
数,也没有最大的整数。
可以表示:
一个物体也没有
正、负数的分界
起点(直尺的0刻度)
计数或计算时,0起占位作用。
0,1,2,3,4,5,…
自
然
数
表示物体个数的0,1,2,3,4,5,…都是自然数。
自然数是整数的一部分。
自然数的个数是无限的,0是最小的自然数,没有最大的自然数。
整数
…,-3,-2,-1,
自然数
最小的自然数
没有最大的自然数
任何非0自然数都是由若干个“1”组成的,“1”是自然数的基本单位。
1个“1”
2个“1”
3个“1”
自然数表示事物的多少时,称为基数,如“7本书”中的“7”就是基数;表示事物的次序时,称为序数,如“第2排”中的“2”就是序数。
分数
把单位“1”平均分成若干份,表示这
样的一份或几份的数叫作分数。
分数单位
分母
分子
表示把单位“1”平均分的份数
表示有这样的几份
分数
真分数
分子<分母
假分数
真分数<1
分子≥分母
假分数≥1
分子是分母的倍数
整数
分子不是
分母的倍数
带分数
整数和真分数合成
小数
像3.25,0.85,2.50,1.2,768.9等这样的数叫作小数。
小数
有限小数
小数部分的位数有限
无限小数
小数部分的位数无限
无限不
循环小数
纯循环小数
循环小数
混循环
小数
一位小数表示十分之几,两位小数表示百分之几……
一个小数由整数部分、小数部分和小数点三部分组成。
0.1=
1
10
0.01=
1
100
0.001=
1
1000
循环节
百分数
百分数与分数
表示一个数是另一个数的百分之几的数
叫作百分数(也叫百分率或百分比)。
百分数的计数单位是 。
1
100
联系:百分数是分母为100的特殊分数。
区别:(1)分数由分子、分母和分数线组成,而百分数通常采用“%”来表示。(2)分数既可以表示一个具体的数量(可以加单位名称),也可以表示两个数量之间的倍比关系;百分数只表示两个数或数量的倍比关系(不可以加单位名称)。
教材第72页第2题
0
1
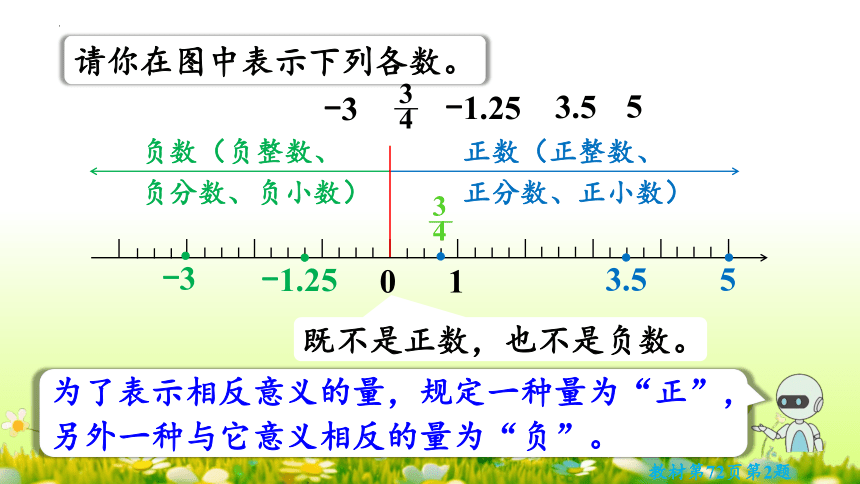
正数(正整数、正分数、正小数)
负数(负整数、负分数、负小数)
为了表示相反意义的量,规定一种量为“正”,另外一种与它意义相反的量为“负”。
既不是正数,也不是负数。
请你在图中表示下列各数。
-1.25
-3
5
3.5
3
4
-3
3
4
-1.25
3.5
5
课堂练习
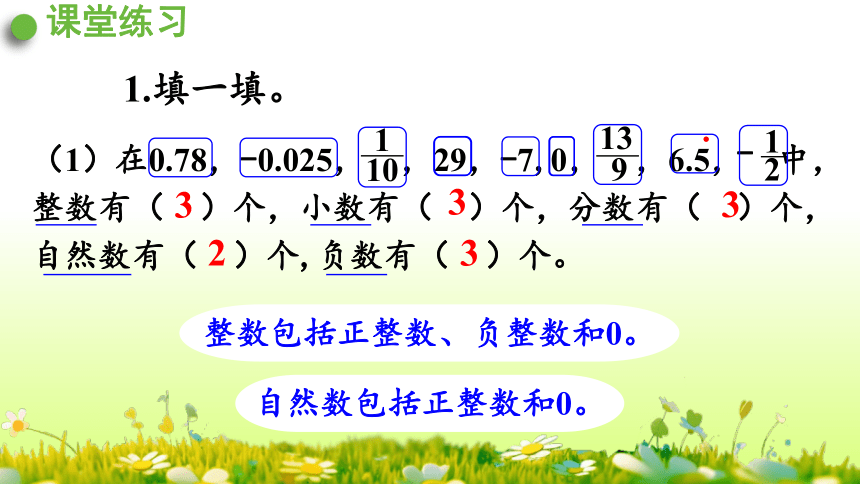
1.填一填。
整数包括正整数、负整数和0。
3
(1)在0.78,-0.025, ,29,-7,0, ,6.5, 中,整数有( )个,小数有( )个,分数有( )个,自然数有( )个,负数有( )个。
.
1
10
13
9
-
1
2
3
3
自然数包括正整数和0。
2
3
(2)下面直线上的点A表示的数是( ),点B表示的数写成小数是( ),点C表示的数写成分数是 。
( )
( )
通过观察可知:点A距离0点1个单位长度,在0的左边是负数,所以点A表示的数是-1。
-1
0.5
5
8
0
-3
1
2
-2
A
B
C
点B在0和1的中间,将1个单位长度平均分成了2份,所以点B表示的小数是0.5。
点C在1和2之间,将1个单位长度平均分成了5份,表示其中的3份,所以点C表示的分数是 ,也就是 。
3
5
1
8
5
(3)六年级一班某次测验的平均成绩为93分。如果数学老师把100分记作+7分,那么98分记作( )分,-3分表示的实际成绩是( )分。
把100分记作+7分,100-7=93(分),说明是把平均成绩93分作为记分标准。
98分比93分多5分就记作+5分;
“-3分”就是比93分少3分,是90分。
+5
90
(4)如图,在正方形ABCD中,点E、F分别为BC、CD的中点,则图中涂色部分的面积占原正方形面积的 。
( )
( )
D
A
C
E
B
原正方形的
1
8
F
原正方形的
1
4
原正方形的
1
4
涂色部分的面积就是原正方形的面积减去其他部分的面积:
1- - -
=
1
4
1
4
1
8
3
8
3
8
2.判一判。
整数
正整数
0
负整数
自然数
(1)自然数都是整数,但整数不都是自然数。( )
(2)小数都比1小。 ( )
(3)分母是9的最简真分数,都不能化成有限小数。
( )
(4)有101粒种子,全部发芽,发芽率为101%。( )
(5)在直线上,-15在-28的右边。( )
√
1.5是小数,比1大。
×
分母是9的真分数都不能化成有限小数。
√
100%
×
0
-28
1
-15
√
<
3.在一个数的后面添一个百分号后,变成的百分数比原来的数小11.88,原来这个数是多少?
在一个数的后面添一个百分号后,变成的百分数是原来数的1%。已知一个数的1%比这个数小11.88,求这个数,用除法。
11.88÷(1-1%)
=11.88÷0.99
=12
答:原来这个数是12。
4.小勇和小丽同时从学校出发,沿着学校门前东西方向的马路各自回家。
(1)如果把小勇向东走了58米记作+58米,那么小丽向西走了42米应该记作什么?
正数和负数用来表示相反意义的量,把小勇向东走记作正数,那么小丽向西走就应该记作负数。
答:小丽向西走了42米应该记作-42米。
(2)在(1)的条件下,小勇转身追赶小丽,如果小勇比小丽每分钟多走5米,多少分钟后小勇可以追上小丽?
追及路程÷速度差=追及时间
(58+42)÷5=20(分)
答:20分钟后小勇可以追上小丽。
4.小勇和小丽同时从学校出发,沿着学校门前东西方向的马路各自回家。
6 整理和复习
1.数与代数
数学人教版六年级下册
第2课时 数的认识(二)
复习导入
什么是十进制计数法?数位和计数单位有什么区别?
教材第72页第3题
用来计量数的单位叫作计数单位,而每个计数单位所占的位置叫作数位。
每相邻两个计数单位之间的进率是10,即通常说的“逢十进一”,这种计数方法叫作十进制计数法。
归纳整理
填写下表,你能提出什么问题?
整数部分 小数点 小数部分
… ( )级 ( )级 ( )级
数位 … 位 位 位 位 位 位 位 位 千位 百位 十位 个位 . 十分位 位 位 …
计数单位 … 十分之一 …
亿
万
个
万
十万
百万
千万
亿
十亿
百亿
千亿
百分
千分
万
十万
百万
千万
亿
十亿
百亿
千亿
百分之一
千分之一
千
百
一(个)
十
十
一(个)
整数部分 小数点 小数部分
… ( )级 ( )级 ( )级
数位 … 位 位 位 位 位 位 位 位 千位 百位 十位 个位 . 十分位 位 位 …
计数单位 … 十分之一 …
亿
万
个
万
十万
百万
千万
亿
十亿
百亿
千亿
百分
千分
万
十万
百万
千万
亿
十亿
百亿
千亿
百分之一
千分之一
千
百
一个数由6个亿、6个千万、6个万、6个百和6个一组成,这个数写作( ),读作( ) 。
660060606
六亿
六千零六万
零六百零六
6
6
6
6
6
0
0
0
0
在对应各数位写上各计数单位的个数
写0占位
读法和写法——整数
读法:
先分级,再从高位到低位,一级一级地读。
读亿级和万级时,先按个级的读法来读,再
在后面加一个“亿”字或“万”字。
每级末尾不管有几个0都不读,其他数位上有1个0或连续几个0,都只读一个零。
读法和写法——整数
写法:
从高位到低位,一级一级地写,先写亿级,再写万级,最后写个级。
哪个数位上有几个计数单位,就在那个数位上写几,一个计数单位也没有,就在那个数位上写0占位。
读法和写法——小数
读法:
先读整数部分,再读小数部分。
整数部分按照整数的读法读(整数部分是0的读作“零”),小数点读作“点”。
小数部分按从左往右的顺序依次读出每一个数位上的数(连续的0要依次全部读出来)。
循环节要读两遍,再加“循环”两个字。
读法和写法——小数
写法:
整数部分按照整数的写法来写,小数点写在个位的右下角。
小数部分顺次写出每一个数位上的数字。
循环小数的循环节至少写两遍,后面再加“…”;也可在循环节的首尾两个数字上面加上“.”。
读法和写法——分数
读法:
先读分母,再将分数线读作“分之”,最后读分子。
分子和分母分别按照整数的读法来读。
读带分数时,先读整数部分,再读分数部分,中间加一个“又”字。
读法和写法——分数
写法:
先写分数线,再写分母,最后写分子。
写带分数时,先写整数部分,再写分数部分,整数部分要对准分数线,距离要紧凑。
在列式计算中,分数线要对准“=”中两横线的中间。
读法和写法——百分数
读法:
先读百分号,读作“百分之”,再读百分号前面的数。
写法:
先写分子,再写百分号。
百分数通常不写成分数形式,而是在原来的分子后面加上“%”。
读法和写法——正数、负数
读法:
先读“+”“-”号,读作“正”“负”,再读后面的数。
写法:
先写“+”或“-”,再写数。
正数的“+”可以省略不写,负数的“-”不可以省略。
据我国商务部统计,2020年前4个月,我国对“一带一路”沿线53个国家非金融类直接投资36620000000元。横线上的数读作( ),改写成用“万”作单位的数是( ),省略“亿”后面的尾数是( )。
3662000万
三百六十六亿二千万
366亿
改写:在万位或亿位的右下角点小数点,去掉小数末尾的“0”,再加上“万”或“亿”字。
省略尾数:将万位或亿位的尾数用“四舍五入”法省略,再加上“万”或“亿”字。
多位数
用“万”或“亿”作单位的数
先改写成分母是10,100,1000,…的分数,再约分
用分子除以分母,除不尽的一般保留两位小数
小数点向右移两位,加上“%”
小数点向左移两位,去掉“%”
写成分数形式,并约分
先改写成小数,再改写成百分数
小数
分数
百分数
分数、小数与
百分数的互化
除不尽的一般保留三位小数
课堂练习
1.填一填。
(1)12.78的计数单位是( ),它有( )个这样的计数单位,至少再加上( )个这样的计数单位就是整数。
0.01
1278
22
12.78的末位“8”在百分位上,所以12.78的计数单位是百分之一或0.01。
比12.78大的最小整数是13,13-12.78=0.22,0.22里有22个0.01。
7.30
(2)7.295保留两位小数是( ),保留三位小数是( )。
7.295
7.295是一个循环小数,它的循环节是“295”,可以写成7.295295…,要保留两位小数,要看千分位上的数,千分位上是5,要向百分位上进1,百分位上是9,继续向十分位上进1,因此保留两位小数是7.30;要保留三位小数,要看万分位上的数,万分位上是2,舍去,因此保留三位小数是7.295。
说说你是怎么想的?
(3)分数单位是 的最大真分数是( ),最小假分数是( )。
1
8
7
8
8
8
分数单位是 即分母是8,真分数的分子小于分母,最大为7;假分数的分子大于或等于分母,最小为8。
1
8
(4)35÷( )= =( )%=( )成
7
10
这道题从 入手思考,根据分数和除法的关系和商不变的规律得 =7÷10=35÷50。
7
10
7
10
50
70
七
10亿是十位数,这个九位数一定是经过“五入”得到的10亿。若要求这个数最大,那么尾数的第一位(千万位)最大是9,这个数最大为999999999;
若要求这个数最小,那么尾数的第一位(千万位)最小是5,这个数最小是950000000。
若要求这个数最大,则它是经过“四舍”得到的10亿,那么尾数的第一位(千万位)为4,其他位为9,这个数最大为1049999999;
若要求这个数最小,则它是经过“五入”得到的10亿,那么尾数的第一位(千万位)最小是5,其他位为0,这个数最小是950000000。
(5)一个整数省略“亿”后面的尾数是10亿,这个数最大是( ),最小是( )。
(6)一个九位数省略“亿”后面的尾数是10亿,这个数最大是( ),最小是( )。
1049999999
950000000
999999999
950000000
小数点位置移动引起小数大小变化的规律
(1)小数点向右移动一位、两位、三位……这个小数就扩大到原来的10倍、100倍、1000倍……小数点向左移动一位、两位、三位……这个小数就缩小到原来的 、 、 ……
(2)如果要把一个小数扩大到原来的10倍、100倍、1000倍……就要把它的小数点向右移动一位、两位、三位……如果要把一个小数缩小到原来的 、 、 ……就要把它的小数点向左移动一位、两位、三位……
1
10
1
1000
1
100
1
10
1
1000
1
100
2.甲、乙两个数的和是496.1,甲数的小数点向右移动一位就等于乙数,甲数是多少?
由“甲数的小数点向右移动一位就等于乙数”可知:甲数×10=乙数。
解:设甲数是x,则乙数是10x。
x+10x=496.1
11x=496.1
x=45.1
答:甲数是45.1。
3.远古时期,人们通过在绳子上打结记录数量,即“结绳计数”。如图,一位母亲在从右往左依次排列的绳子上打结,满七进一,用来记录孩子出生后的天数。你知道这个孩子出生了多少天吗?
一个结表示1天
左边 中间 右边
4个结 3个结 6个结
4×7×7 3×7 6×1
=196+21+6
=223(天)
答:这个孩子出生了223天。
一个结表示7天
一个结表示7个7天
+ +
6 整理和复习
1.数与代数
数学人教版六年级下册
第3课时 数的认识(三)
复习导入
你能根据a÷b=c(a、b、c均为整数,且b≠0)说明因数和倍数的含义吗?
教材第72页第4题
如果a÷b=c(a、b、c均为均为整数,且b≠0),那么a是b和c的倍数,b和c是a的因数。
研究因数和倍数时,我们所说的数是自然数(一般不包括0)。
(1)一个数的因数的个数是( )的,最小的因数是( ),最大的因数是( )。
归纳整理
因数和倍数的特征,你能试着填一填吗?
(2)一个数的倍数的个数是( )的,最小的倍数是( ),( )最大的倍数。
(3)( )是任何自然数的因数,任何自然数都是( )的倍数。
有限
1
它本身
无限
它本身
没有
1
1
你能说一说2、3、5的倍数的特征吗?
个位上是0,2,4,6,8的数都是2的倍数
各数位上的数字和是3的倍数的数就是3的倍数
个位上是0或5的数都是5的倍数
同时是2、3、5的倍数的特征:各数位上的数字和是3的倍数,且个位上是0的数。
几个数公有的因数叫作这几个数的公因数。其中最大的一个公因数叫作这几个数的最大公因数。
怎样求两个数的最大公因数呢?
列举法:先写出这两个数的所有因数,再找出这两个数的公因数,从公因数中找出最大公因数。
短除法:是分解质因数法的简便形式,用两个数公有的质因数同时去除这两个数,除到所得的商只有公因数1,再将所有的除数相乘。
列举法
筛选法
短除法
分解质因数法
筛选法:先找出较小数的所有因数,再从中圈出较大数的因数,并从中找到最大的一个。
分解质因数法:先将这两个数分别分解质因数,再从分解的质因数中找出这两个数公有的质因数,所有公有的质因数相乘的积就是这两个数的最大公因数。
几个数公有的倍数叫作这几个数的公倍数。其中最小的一个公倍数叫作这几个数的最小公倍数。
怎样求两个数的最小公倍数呢?
列举法
筛选法
短除法
分解质因数法
列举法:先分别写出这两个数各自的倍数,再从中找出公倍数和最小公倍数。
筛选法:先写出一个数的倍数,再从中按从小到大的顺序圈出另一个数的倍数,第一个圈出的就是这两个数的最小公倍数。
分解质因数法:先将这两个数分解质因数,再把这两个数公有的质因数和各自独有的质因数相乘,所得的积就是这两个数的最小公倍数。
短除法:用两个数公有的质因数同时去除这两个数,直到所得的商只有公因数1,再将所有的商和除数相乘,即可求出这两个数的最小公倍数。
(1)两个数有倍数关系:
较小数是这两个数的最大公因数,
较大数是这两个数的最小公倍数。
(2)两个数互质:
这两个数的最大公因数是1,
最小公倍数是这两个数的乘积。
求两个数的最大公因数和最小公倍数的特殊情况
关于质数和合数的相关知识,你会填吗?
(1)一个数( ),这样的数叫作质数(或素数)。
只有1和它本身两个因数
(2)一个数( ),这样的数叫作合数。
如果除了1和它本身还有别的因数
(3)( )的两个数,叫作互质数。
公因数只有1
(4)( )既不是质数,也不是合数。
1
关于奇数和偶数的相关知识,你会填吗?
(1)整数中,( )叫作偶数。
是2的倍数的数
(2)整数中,( )叫作奇数。
不是2的倍数的数
(3)在自然数中,最小的奇数是( ),没有最大的奇数;最小的偶数是( ),没有最大的偶数。
1
(4)偶数±偶数=( ) 奇数±奇数=( )
奇数±偶数=( ) 偶数×偶数=( )
偶数×奇数=( ) 奇数×奇数=( )
偶数
0
偶数
奇数
偶数
偶数
奇数
课堂练习
1.填一填。
一个数的最小倍数和最大因数都是它本身。
(1)一个数的最小倍数减它的最大因数,差是( );一个数的最小倍数除以它的最大因数,商是( )。
0
1
(2)在括号里填上合适的质数。
24=( )+( )=( )+( )=( )+( )
24以内的质数有2、3、5、7、11、13、17、19、23
5 19
7 17
11 13
(4)52和130的最大公因数是( )。
(3)用0、1、2组成的三位数中,偶数有( )个。
用0、1、2组成的三位数有210、201、120、102
3
用短除法分解质因数:
52 130
2×13=26
26
2
26 65
13
2 5
(5)如果a÷b=6(a、b均为非0自然数),那么a和b的最大公因数是( ),最小公倍数是( )。
a和b有倍数关系,因此其中的较小数b是它们的最大公因数,较大数a是它们的最小公倍数。
b
(6)三位数12□既是3的倍数又是5的倍数,□里可以填( )。
a
0
当它是5的倍数时,□里可以填的数是0或5,其中只有0可以让这个数既是3的倍数又是5的倍数。
2.判一判。
(1)若n是自然数,则2n+1一定是奇数。( )
(2)45=5×9,5和9都是45的质因数。 ( )
(3)因为24÷3=8,所以24是倍数,3是因数。( )
(4)两个质数相乘的积还是质数。( )
(5)一个自然数越大,它的因数就越多。( )
√
×
×
×
×
n是自然数,2n一定是偶数,偶数加1一定是奇数。
9不是质数
倍数和因数是相互依存的,不能单独说谁是因数或倍数。
所得积的因数至少有1和这两个质数还有它本身,是合数。
因数的个数与自然数的大小无关。
3.选一选。
(1)一个两位数既是2的倍数,又含有因数3,这个两位数最大是( )。
C
A.99 B.98 C.96 D.90
不是2的倍数
不是3的倍数
符合题意
不是3的倍数
是3的倍数
将错误选项排除就能找到正确的选项啦!
(2)与偶数a相邻的2个偶数分别是( )。
D
A.a-1和a+1 B.a-1和a+3
C.a-3和a+3 D.a-2和a+2
(3)两个整数的和为偶数,其中一个整数是奇数,另一个整数一定是( )。
C
A.质数 B.合数 C.奇数 D.偶数
相邻的两个偶数之间相差2
因为“偶数-奇数=奇数”,只能确定另一个数是奇数,不能确定是质数还是合数。
(4)如下图,下面各说法错误的是( )。
A
A.甲和乙公有的质因数是1
B.甲和乙的最大公因数是8
C.甲和乙都是偶数
D.甲和乙的最小公倍数是96
甲和乙公有的质因数应该是2,1不是质数;
甲和乙的最大公因数能从图中看出来,是8;
甲和乙都有公因数2,因此甲和乙都是偶数;
甲是24,乙是32,最小公倍数是96。
甲的因数
乙的因数
甲和乙的公因数
1、2、
4、8
3、6、
12、24
16、32、
2
小林的爸爸是每4天休息一天,妈妈是每5天休息一天;两人同时休息的日子之间间隔的天数是4和5的公倍数;4和5互质,最小公倍数就是它们的乘积。
4×5=20(天)
6月1日+20天=6月21日
答:下一次同时在家休息是6月21日。
4.小林的爸爸每上班3天休息1天,妈妈每上班4天休息1天。6月1日他们同时在家休息,下一次同时在家休息是几月几日?
5.某工厂大约有100人,将他们按每组8人分组,多5人,按每组12人分组,也多5人。这个工厂有多少人?
(总人数-5)是8和12的公倍数。
8和12的公倍数有24、48、72、96、120……
其中最接近100的是96。
96+5=101(人)
答:这个工厂有101人。
6.一个三位数既是2的倍数,又是3的倍数,而且个位、十位上的数字相同,这个三位数最大是多少?
综合题意,从“这个三位数最大”考虑,百位上最大选9;再考虑“是2的倍数”,个位上可能是0、2、4、6或8;从900、922、944、966、988里选择3的倍数,符合条件的是900和966。
答:这个三位数最大是966。
6 整理和复习
1.数与代数
数学人教版六年级下册
第4课时 练习
练习巩固
1.填空。
零下为负,负数前面的“-”不可以省略。
(1)2008年8月3日,气象部门在新疆吐鲁番盆地的艾丁湖观测到的最高气温是49.7 ℃,可记作 ℃。1969年2月13日,气象部门在黑龙江漠河观测到的最低气温是零下52.3 ℃,可记作 ℃。
-52.3
49.7或+49.7
零上为正,正数前面的“+”可以省略不写。
(教材第73页练习十四)
较小数
可以用100-100×70%=30(元),也可用100×(1-70%)=30(元)。
(2)如果a÷b=c(a、b、c均为整数,且b≠0),那么a和b的最大公因数是_____,最小公倍数是_____。
a
b
a和b有倍数关系
较大数
(3)一种商品打七折销售,“七折”表示现价是原价的( )%。如果这种商品原价是100元,付款时要少付( )元。
70
30
2.下表是我国2017年、2019年、2021年全国城镇常住人口数量、全年粮食产量和全年消费品零售总额的相关数据。
年份 全国城镇常住人口数量/万人 全年粮食产量/万吨 全年消费品零售总额/亿元
2017 81347 61791 366262
2019 84843 66384 411649
2021 91425 68285 440823
年份 全国城镇常住人口数量/万人 全年粮食产量/万吨 全年消费品零售总额/亿元
2017 81347 61791 366262
2019 84843 66384 411649
2021 91425 68285 440823
(1)2017年,全国城镇常住人口约为_____亿人。(结果保留两位小数。)
8.13
年份 全国城镇常住人口数量/万人 全年粮食产量/万吨 全年消费品零售总额/亿元
2017 81347 61791 366262
2019 84843 66384 411649
2021 91425 68285 440823
(2)2019年,全年粮食产量约为_____亿吨。(结果保留两位小数。)
6.64
年份 全国城镇常住人口数量/万人 全年粮食产量/万吨 全年消费品零售总额/亿元
2017 81347 61791 366262
2019 84843 66384 411649
2021 91425 68285 440823
(3)2021年,全年消费品零售总额约为_____万亿元。(结果保留两位小数。)
44.08
年份 全国城镇常住人口数量/万人 全年粮食产量/万吨 全年消费品零售总额/亿元
2017 81347 61791 366262
2019 84843 66384 411649
2021 91425 68285 440823
(4)根据上表,你还能提出什么数学问题?
2021年全国城镇常住人口数量比2017年增长百分之几?
3.说出下面各数中“6”表示的含义。
63
0.56
603.7
6
7
“6”在十位上表示“6个十”
十位的计数单位是“十”
“6”在百分位上表示“6个0.01”
百分位的计数单位是“0.01”
“6”在百位上表示“6个百”
百位的计数单位是“百”
“6”在分子上表示“6个 ”
1
7
分数单位是“ ”
1
7
4.填空,使每横行的各数相等。
小数 分数 百分数
0.4
80%
4
5
3
4
25
40%
75%
0.75
0.8
= =
4
10
小数点向右移两位,加上“%”
分子÷分母
分子分母同时×25
约分
小数点向左移两位,去掉“%”
先改写成分母是10,100,1000,…的分数,再约分
用分子除以分母,除不尽的一般保留两位小数
小数点向右移两位,加上“%”
小数点向左移两位,去掉“%”
写成分数形式,并约分
先改写成小数,再改写成百分数
小数
分数
百分数
分数、小数与
百分数的互化
除不尽的一般保留三位小数
5.数字2、3、4、5能组成多少个没有重复数字的两位数?
十位是2:
23
24
25
十位是3:
32
34
35
十位是4:
42
43
45
十位是5:
52
53
54
(1)这些两位数中,哪些是奇数?哪些是偶数?
答:奇数有23、25、35、43、45、53;
偶数有24、32、34、42、52、54。
(2)这些两位数中,哪些是质数?哪些是合数?
答:质数有23、43、53;合数有24、25、32、34、35、42、45、52、54。
5.数字2、3、4、5能组成多少个没有重复数字的两位数?
十位是2:
23
24
25
十位是3:
32
34
35
十位是4:
42
43
45
十位是5:
52
53
54
(3)这些两位数中,哪些是2的倍数?哪些是3的倍数?哪些是5的倍数?
答:2的倍数有24、32、34、42、52、54;3的倍数有24、42、45、54;5的倍数有25、35、45。
(4)这些两位数中,2和3的公倍数是 ,3和5的公倍数是 。
24、42、54
45
都从合数里选择
从3的倍数里选择偶数
从3的倍数里选择5的倍数
6.判断下面的说法是否正确,并说一说你的理由。
(1)把0.56扩大到它的100倍是560。
(2)0是正数。
(3)假分数的倒数一定都是真分数。
(4)所有的偶数都是合数。
(5)a(a为整数,a>1)的所有因数都小于a。
小数点向右移2位,应该是56。
不正确
不正确
不正确
不正确
不正确
0既不是正数也不是负数。
分子分母相同的假分数的倒数还是假分数。
2是偶数但不是合数。
a的因数可以是它本身。
7.找规律,填数。
(1)0.9,0.99,0.999,0.9999,( ),…,这列数越来越大,越来越接近( )。
0.99999
1
1个9
2个9
3个9
4个9
5个9
0.9
1
+0.1
0.99
1
+0.01
0.999
1
+0.001
+0.0001
0.9999
1
……
1
64
(2) , , , , ,( ),…,这列数越来越小,越来越接近( )。
1
32
1
16
1
8
1
4
1
2
1
32
1
16
1
8
1
4
1
2
1
64
1
64
×
1
2
×
1
2
×
1
2
×
1
2
×
1
2
1
2
1
4
1
8
1
16
1
32
0
8.比较 、 、 、 的大小,你能发现什么?
1
2
5
6
2
3
3
4
< < <
1
2
5
6
2
3
3
4
1
2
5
6
2
3
3
4
8.比较 、 、 、 的大小,你能发现什么?
1
2
5
6
2
3
3
4
< < <
1
2
5
6
2
3
3
4
猜
想:
17
18
19
20
<
验证:
17
18
170
180
=
19
20
171
180
=
根据你发现的规律猜一下 与 哪个更大,并设法验证。
17
18
19
20
170
180
<
171
180
17
18
19
20
<
所以
我发现这些分数的分子都比分母小1,当分子、分母越大时,这个分数就越大。
因为
9.*一箱苹果,如果每8个装一盒,还剩余6个;如果每10个装一盒,也剩余6个。这箱苹果至少有多少个?
由题意可知,(苹果数-6)是8和10的公倍数。
8和10的最小公倍数是40。
40+6=46(个)
答:这箱苹果至少有46个。
求至少有多少个,就是求8和10的最小公倍数加6是多少。
拓展提升
1.把一张长32厘米、宽24厘米的长方形剪成同样大小,且面积尽可能大的正方形(没有剩余)。一共可以剪多少个这样的正方形?
剪成的形状是正方形,说明正方形的边长是长方形长和宽的公因数;要正方形尽可能大,就是求长方形长和宽的最大公因数。
因为32和24的最大公因数是8,所以正方形的边长是8厘米。
(32÷8)×(24÷8)=12(个)
答:一共可以剪12个这样的正方形。
2.表演队在操场上列队,人数在90~110范围内,且他们排成3列无余,排成5列差2人,排成7列差4人,共多少人?
由题意可知,(总人数-3)是3、5、7的公倍数。
3、5、7的公倍数有105、210……符合题意的是105。
105+3=108(人)
答:共有108人。
余3人
余3人
余3人
求解同余同差问题,就是先求几个数的公倍数,再加上同余或减去同差。
Thank you!
6 整理和复习
1.数与代数
数学人教版六年级下册
第1课时 数的认识(一)
情境导入
你学过哪些数?它们在生活中有哪些应用?阅读下面的资料,你能发现什么?
第24届冬季奥林匹克运动会于2022年2月4日至2月20日在北京和河北张家口举行。
教材第71页
来自91个国家和地区的代表团总计2880名运动员参加了7个大项(包括15个分项、109个小项)的比赛。中国代表团共有176名运动员参加了比赛,其中女运动员87人,占49.43%;男运动员89人,占50.57%;运动员平均年龄25.2岁。中国代表团获得了9枚金牌、4枚银牌和2枚铜牌,列金牌榜第三位,金牌数和奖牌数均创历史新高。共有1.9万名志愿者参加了志愿服务。本届冬奥会践行“绿色办奥”的理念,实现了低碳、节能、环保的目标。本届冬奥会的主火炬采用“微火”技术,其碳排放量大约只有传统点火方式的;国家速滑馆“冰丝带”采用二氧化碳制冷技术,碳排放量约是传统制冰技术的。设计团队开发的智慧场馆系统,能将“冰丝带” 的冰面温度精确地维持在-11~-10 ℃。
小数
分数
负数
整数
百分数
归纳整理
教材第72页第1题
你能把学过的数整理成图表来表示吗?
数
整数
分数(小数、
百分数)
正整数
0
负整数
自然数
小数
分数
百分数
有限小数
无限小数
循环小数
无限不循环小数
真分数
假分数(带分数)
注意:无限不循环小数不能转化为分数。
也可以这样分
数
正数
负数
正整数
0
正分数(正小数、正百分数)
自然数
负整数
负分数(负小数、负百分数)
整数
正整数
0
负整数
像1,2,3,…这样的数叫作正整数。
像-1,-2,-3,…这样的数叫作负整数。
整数
正整数的个数是无限的,最小的正整数是1,没有最大的正整数。
负整数的个数是无限的,最大的负整数是-1,没有最小的负整数。
像…,-3,-2,-1,0,1,2,3,…
这样的数统称为整数。
整数的个数是无限的,没有最小的整
数,也没有最大的整数。
可以表示:
一个物体也没有
正、负数的分界
起点(直尺的0刻度)
计数或计算时,0起占位作用。
0,1,2,3,4,5,…
自
然
数
表示物体个数的0,1,2,3,4,5,…都是自然数。
自然数是整数的一部分。
自然数的个数是无限的,0是最小的自然数,没有最大的自然数。
整数
…,-3,-2,-1,
自然数
最小的自然数
没有最大的自然数
任何非0自然数都是由若干个“1”组成的,“1”是自然数的基本单位。
1个“1”
2个“1”
3个“1”
自然数表示事物的多少时,称为基数,如“7本书”中的“7”就是基数;表示事物的次序时,称为序数,如“第2排”中的“2”就是序数。
分数
把单位“1”平均分成若干份,表示这
样的一份或几份的数叫作分数。
分数单位
分母
分子
表示把单位“1”平均分的份数
表示有这样的几份
分数
真分数
分子<分母
假分数
真分数<1
分子≥分母
假分数≥1
分子是分母的倍数
整数
分子不是
分母的倍数
带分数
整数和真分数合成
小数
像3.25,0.85,2.50,1.2,768.9等这样的数叫作小数。
小数
有限小数
小数部分的位数有限
无限小数
小数部分的位数无限
无限不
循环小数
纯循环小数
循环小数
混循环
小数
一位小数表示十分之几,两位小数表示百分之几……
一个小数由整数部分、小数部分和小数点三部分组成。
0.1=
1
10
0.01=
1
100
0.001=
1
1000
循环节
百分数
百分数与分数
表示一个数是另一个数的百分之几的数
叫作百分数(也叫百分率或百分比)。
百分数的计数单位是 。
1
100
联系:百分数是分母为100的特殊分数。
区别:(1)分数由分子、分母和分数线组成,而百分数通常采用“%”来表示。(2)分数既可以表示一个具体的数量(可以加单位名称),也可以表示两个数量之间的倍比关系;百分数只表示两个数或数量的倍比关系(不可以加单位名称)。
教材第72页第2题
0
1
正数(正整数、正分数、正小数)
负数(负整数、负分数、负小数)
为了表示相反意义的量,规定一种量为“正”,另外一种与它意义相反的量为“负”。
既不是正数,也不是负数。
请你在图中表示下列各数。
-1.25
-3
5
3.5
3
4
-3
3
4
-1.25
3.5
5
课堂练习
1.填一填。
整数包括正整数、负整数和0。
3
(1)在0.78,-0.025, ,29,-7,0, ,6.5, 中,整数有( )个,小数有( )个,分数有( )个,自然数有( )个,负数有( )个。
.
1
10
13
9
-
1
2
3
3
自然数包括正整数和0。
2
3
(2)下面直线上的点A表示的数是( ),点B表示的数写成小数是( ),点C表示的数写成分数是 。
( )
( )
通过观察可知:点A距离0点1个单位长度,在0的左边是负数,所以点A表示的数是-1。
-1
0.5
5
8
0
-3
1
2
-2
A
B
C
点B在0和1的中间,将1个单位长度平均分成了2份,所以点B表示的小数是0.5。
点C在1和2之间,将1个单位长度平均分成了5份,表示其中的3份,所以点C表示的分数是 ,也就是 。
3
5
1
8
5
(3)六年级一班某次测验的平均成绩为93分。如果数学老师把100分记作+7分,那么98分记作( )分,-3分表示的实际成绩是( )分。
把100分记作+7分,100-7=93(分),说明是把平均成绩93分作为记分标准。
98分比93分多5分就记作+5分;
“-3分”就是比93分少3分,是90分。
+5
90
(4)如图,在正方形ABCD中,点E、F分别为BC、CD的中点,则图中涂色部分的面积占原正方形面积的 。
( )
( )
D
A
C
E
B
原正方形的
1
8
F
原正方形的
1
4
原正方形的
1
4
涂色部分的面积就是原正方形的面积减去其他部分的面积:
1- - -
=
1
4
1
4
1
8
3
8
3
8
2.判一判。
整数
正整数
0
负整数
自然数
(1)自然数都是整数,但整数不都是自然数。( )
(2)小数都比1小。 ( )
(3)分母是9的最简真分数,都不能化成有限小数。
( )
(4)有101粒种子,全部发芽,发芽率为101%。( )
(5)在直线上,-15在-28的右边。( )
√
1.5是小数,比1大。
×
分母是9的真分数都不能化成有限小数。
√
100%
×
0
-28
1
-15
√
<
3.在一个数的后面添一个百分号后,变成的百分数比原来的数小11.88,原来这个数是多少?
在一个数的后面添一个百分号后,变成的百分数是原来数的1%。已知一个数的1%比这个数小11.88,求这个数,用除法。
11.88÷(1-1%)
=11.88÷0.99
=12
答:原来这个数是12。
4.小勇和小丽同时从学校出发,沿着学校门前东西方向的马路各自回家。
(1)如果把小勇向东走了58米记作+58米,那么小丽向西走了42米应该记作什么?
正数和负数用来表示相反意义的量,把小勇向东走记作正数,那么小丽向西走就应该记作负数。
答:小丽向西走了42米应该记作-42米。
(2)在(1)的条件下,小勇转身追赶小丽,如果小勇比小丽每分钟多走5米,多少分钟后小勇可以追上小丽?
追及路程÷速度差=追及时间
(58+42)÷5=20(分)
答:20分钟后小勇可以追上小丽。
4.小勇和小丽同时从学校出发,沿着学校门前东西方向的马路各自回家。
6 整理和复习
1.数与代数
数学人教版六年级下册
第2课时 数的认识(二)
复习导入
什么是十进制计数法?数位和计数单位有什么区别?
教材第72页第3题
用来计量数的单位叫作计数单位,而每个计数单位所占的位置叫作数位。
每相邻两个计数单位之间的进率是10,即通常说的“逢十进一”,这种计数方法叫作十进制计数法。
归纳整理
填写下表,你能提出什么问题?
整数部分 小数点 小数部分
… ( )级 ( )级 ( )级
数位 … 位 位 位 位 位 位 位 位 千位 百位 十位 个位 . 十分位 位 位 …
计数单位 … 十分之一 …
亿
万
个
万
十万
百万
千万
亿
十亿
百亿
千亿
百分
千分
万
十万
百万
千万
亿
十亿
百亿
千亿
百分之一
千分之一
千
百
一(个)
十
十
一(个)
整数部分 小数点 小数部分
… ( )级 ( )级 ( )级
数位 … 位 位 位 位 位 位 位 位 千位 百位 十位 个位 . 十分位 位 位 …
计数单位 … 十分之一 …
亿
万
个
万
十万
百万
千万
亿
十亿
百亿
千亿
百分
千分
万
十万
百万
千万
亿
十亿
百亿
千亿
百分之一
千分之一
千
百
一个数由6个亿、6个千万、6个万、6个百和6个一组成,这个数写作( ),读作( ) 。
660060606
六亿
六千零六万
零六百零六
6
6
6
6
6
0
0
0
0
在对应各数位写上各计数单位的个数
写0占位
读法和写法——整数
读法:
先分级,再从高位到低位,一级一级地读。
读亿级和万级时,先按个级的读法来读,再
在后面加一个“亿”字或“万”字。
每级末尾不管有几个0都不读,其他数位上有1个0或连续几个0,都只读一个零。
读法和写法——整数
写法:
从高位到低位,一级一级地写,先写亿级,再写万级,最后写个级。
哪个数位上有几个计数单位,就在那个数位上写几,一个计数单位也没有,就在那个数位上写0占位。
读法和写法——小数
读法:
先读整数部分,再读小数部分。
整数部分按照整数的读法读(整数部分是0的读作“零”),小数点读作“点”。
小数部分按从左往右的顺序依次读出每一个数位上的数(连续的0要依次全部读出来)。
循环节要读两遍,再加“循环”两个字。
读法和写法——小数
写法:
整数部分按照整数的写法来写,小数点写在个位的右下角。
小数部分顺次写出每一个数位上的数字。
循环小数的循环节至少写两遍,后面再加“…”;也可在循环节的首尾两个数字上面加上“.”。
读法和写法——分数
读法:
先读分母,再将分数线读作“分之”,最后读分子。
分子和分母分别按照整数的读法来读。
读带分数时,先读整数部分,再读分数部分,中间加一个“又”字。
读法和写法——分数
写法:
先写分数线,再写分母,最后写分子。
写带分数时,先写整数部分,再写分数部分,整数部分要对准分数线,距离要紧凑。
在列式计算中,分数线要对准“=”中两横线的中间。
读法和写法——百分数
读法:
先读百分号,读作“百分之”,再读百分号前面的数。
写法:
先写分子,再写百分号。
百分数通常不写成分数形式,而是在原来的分子后面加上“%”。
读法和写法——正数、负数
读法:
先读“+”“-”号,读作“正”“负”,再读后面的数。
写法:
先写“+”或“-”,再写数。
正数的“+”可以省略不写,负数的“-”不可以省略。
据我国商务部统计,2020年前4个月,我国对“一带一路”沿线53个国家非金融类直接投资36620000000元。横线上的数读作( ),改写成用“万”作单位的数是( ),省略“亿”后面的尾数是( )。
3662000万
三百六十六亿二千万
366亿
改写:在万位或亿位的右下角点小数点,去掉小数末尾的“0”,再加上“万”或“亿”字。
省略尾数:将万位或亿位的尾数用“四舍五入”法省略,再加上“万”或“亿”字。
多位数
用“万”或“亿”作单位的数
先改写成分母是10,100,1000,…的分数,再约分
用分子除以分母,除不尽的一般保留两位小数
小数点向右移两位,加上“%”
小数点向左移两位,去掉“%”
写成分数形式,并约分
先改写成小数,再改写成百分数
小数
分数
百分数
分数、小数与
百分数的互化
除不尽的一般保留三位小数
课堂练习
1.填一填。
(1)12.78的计数单位是( ),它有( )个这样的计数单位,至少再加上( )个这样的计数单位就是整数。
0.01
1278
22
12.78的末位“8”在百分位上,所以12.78的计数单位是百分之一或0.01。
比12.78大的最小整数是13,13-12.78=0.22,0.22里有22个0.01。
7.30
(2)7.295保留两位小数是( ),保留三位小数是( )。
7.295
7.295是一个循环小数,它的循环节是“295”,可以写成7.295295…,要保留两位小数,要看千分位上的数,千分位上是5,要向百分位上进1,百分位上是9,继续向十分位上进1,因此保留两位小数是7.30;要保留三位小数,要看万分位上的数,万分位上是2,舍去,因此保留三位小数是7.295。
说说你是怎么想的?
(3)分数单位是 的最大真分数是( ),最小假分数是( )。
1
8
7
8
8
8
分数单位是 即分母是8,真分数的分子小于分母,最大为7;假分数的分子大于或等于分母,最小为8。
1
8
(4)35÷( )= =( )%=( )成
7
10
这道题从 入手思考,根据分数和除法的关系和商不变的规律得 =7÷10=35÷50。
7
10
7
10
50
70
七
10亿是十位数,这个九位数一定是经过“五入”得到的10亿。若要求这个数最大,那么尾数的第一位(千万位)最大是9,这个数最大为999999999;
若要求这个数最小,那么尾数的第一位(千万位)最小是5,这个数最小是950000000。
若要求这个数最大,则它是经过“四舍”得到的10亿,那么尾数的第一位(千万位)为4,其他位为9,这个数最大为1049999999;
若要求这个数最小,则它是经过“五入”得到的10亿,那么尾数的第一位(千万位)最小是5,其他位为0,这个数最小是950000000。
(5)一个整数省略“亿”后面的尾数是10亿,这个数最大是( ),最小是( )。
(6)一个九位数省略“亿”后面的尾数是10亿,这个数最大是( ),最小是( )。
1049999999
950000000
999999999
950000000
小数点位置移动引起小数大小变化的规律
(1)小数点向右移动一位、两位、三位……这个小数就扩大到原来的10倍、100倍、1000倍……小数点向左移动一位、两位、三位……这个小数就缩小到原来的 、 、 ……
(2)如果要把一个小数扩大到原来的10倍、100倍、1000倍……就要把它的小数点向右移动一位、两位、三位……如果要把一个小数缩小到原来的 、 、 ……就要把它的小数点向左移动一位、两位、三位……
1
10
1
1000
1
100
1
10
1
1000
1
100
2.甲、乙两个数的和是496.1,甲数的小数点向右移动一位就等于乙数,甲数是多少?
由“甲数的小数点向右移动一位就等于乙数”可知:甲数×10=乙数。
解:设甲数是x,则乙数是10x。
x+10x=496.1
11x=496.1
x=45.1
答:甲数是45.1。
3.远古时期,人们通过在绳子上打结记录数量,即“结绳计数”。如图,一位母亲在从右往左依次排列的绳子上打结,满七进一,用来记录孩子出生后的天数。你知道这个孩子出生了多少天吗?
一个结表示1天
左边 中间 右边
4个结 3个结 6个结
4×7×7 3×7 6×1
=196+21+6
=223(天)
答:这个孩子出生了223天。
一个结表示7天
一个结表示7个7天
+ +
6 整理和复习
1.数与代数
数学人教版六年级下册
第3课时 数的认识(三)
复习导入
你能根据a÷b=c(a、b、c均为整数,且b≠0)说明因数和倍数的含义吗?
教材第72页第4题
如果a÷b=c(a、b、c均为均为整数,且b≠0),那么a是b和c的倍数,b和c是a的因数。
研究因数和倍数时,我们所说的数是自然数(一般不包括0)。
(1)一个数的因数的个数是( )的,最小的因数是( ),最大的因数是( )。
归纳整理
因数和倍数的特征,你能试着填一填吗?
(2)一个数的倍数的个数是( )的,最小的倍数是( ),( )最大的倍数。
(3)( )是任何自然数的因数,任何自然数都是( )的倍数。
有限
1
它本身
无限
它本身
没有
1
1
你能说一说2、3、5的倍数的特征吗?
个位上是0,2,4,6,8的数都是2的倍数
各数位上的数字和是3的倍数的数就是3的倍数
个位上是0或5的数都是5的倍数
同时是2、3、5的倍数的特征:各数位上的数字和是3的倍数,且个位上是0的数。
几个数公有的因数叫作这几个数的公因数。其中最大的一个公因数叫作这几个数的最大公因数。
怎样求两个数的最大公因数呢?
列举法:先写出这两个数的所有因数,再找出这两个数的公因数,从公因数中找出最大公因数。
短除法:是分解质因数法的简便形式,用两个数公有的质因数同时去除这两个数,除到所得的商只有公因数1,再将所有的除数相乘。
列举法
筛选法
短除法
分解质因数法
筛选法:先找出较小数的所有因数,再从中圈出较大数的因数,并从中找到最大的一个。
分解质因数法:先将这两个数分别分解质因数,再从分解的质因数中找出这两个数公有的质因数,所有公有的质因数相乘的积就是这两个数的最大公因数。
几个数公有的倍数叫作这几个数的公倍数。其中最小的一个公倍数叫作这几个数的最小公倍数。
怎样求两个数的最小公倍数呢?
列举法
筛选法
短除法
分解质因数法
列举法:先分别写出这两个数各自的倍数,再从中找出公倍数和最小公倍数。
筛选法:先写出一个数的倍数,再从中按从小到大的顺序圈出另一个数的倍数,第一个圈出的就是这两个数的最小公倍数。
分解质因数法:先将这两个数分解质因数,再把这两个数公有的质因数和各自独有的质因数相乘,所得的积就是这两个数的最小公倍数。
短除法:用两个数公有的质因数同时去除这两个数,直到所得的商只有公因数1,再将所有的商和除数相乘,即可求出这两个数的最小公倍数。
(1)两个数有倍数关系:
较小数是这两个数的最大公因数,
较大数是这两个数的最小公倍数。
(2)两个数互质:
这两个数的最大公因数是1,
最小公倍数是这两个数的乘积。
求两个数的最大公因数和最小公倍数的特殊情况
关于质数和合数的相关知识,你会填吗?
(1)一个数( ),这样的数叫作质数(或素数)。
只有1和它本身两个因数
(2)一个数( ),这样的数叫作合数。
如果除了1和它本身还有别的因数
(3)( )的两个数,叫作互质数。
公因数只有1
(4)( )既不是质数,也不是合数。
1
关于奇数和偶数的相关知识,你会填吗?
(1)整数中,( )叫作偶数。
是2的倍数的数
(2)整数中,( )叫作奇数。
不是2的倍数的数
(3)在自然数中,最小的奇数是( ),没有最大的奇数;最小的偶数是( ),没有最大的偶数。
1
(4)偶数±偶数=( ) 奇数±奇数=( )
奇数±偶数=( ) 偶数×偶数=( )
偶数×奇数=( ) 奇数×奇数=( )
偶数
0
偶数
奇数
偶数
偶数
奇数
课堂练习
1.填一填。
一个数的最小倍数和最大因数都是它本身。
(1)一个数的最小倍数减它的最大因数,差是( );一个数的最小倍数除以它的最大因数,商是( )。
0
1
(2)在括号里填上合适的质数。
24=( )+( )=( )+( )=( )+( )
24以内的质数有2、3、5、7、11、13、17、19、23
5 19
7 17
11 13
(4)52和130的最大公因数是( )。
(3)用0、1、2组成的三位数中,偶数有( )个。
用0、1、2组成的三位数有210、201、120、102
3
用短除法分解质因数:
52 130
2×13=26
26
2
26 65
13
2 5
(5)如果a÷b=6(a、b均为非0自然数),那么a和b的最大公因数是( ),最小公倍数是( )。
a和b有倍数关系,因此其中的较小数b是它们的最大公因数,较大数a是它们的最小公倍数。
b
(6)三位数12□既是3的倍数又是5的倍数,□里可以填( )。
a
0
当它是5的倍数时,□里可以填的数是0或5,其中只有0可以让这个数既是3的倍数又是5的倍数。
2.判一判。
(1)若n是自然数,则2n+1一定是奇数。( )
(2)45=5×9,5和9都是45的质因数。 ( )
(3)因为24÷3=8,所以24是倍数,3是因数。( )
(4)两个质数相乘的积还是质数。( )
(5)一个自然数越大,它的因数就越多。( )
√
×
×
×
×
n是自然数,2n一定是偶数,偶数加1一定是奇数。
9不是质数
倍数和因数是相互依存的,不能单独说谁是因数或倍数。
所得积的因数至少有1和这两个质数还有它本身,是合数。
因数的个数与自然数的大小无关。
3.选一选。
(1)一个两位数既是2的倍数,又含有因数3,这个两位数最大是( )。
C
A.99 B.98 C.96 D.90
不是2的倍数
不是3的倍数
符合题意
不是3的倍数
是3的倍数
将错误选项排除就能找到正确的选项啦!
(2)与偶数a相邻的2个偶数分别是( )。
D
A.a-1和a+1 B.a-1和a+3
C.a-3和a+3 D.a-2和a+2
(3)两个整数的和为偶数,其中一个整数是奇数,另一个整数一定是( )。
C
A.质数 B.合数 C.奇数 D.偶数
相邻的两个偶数之间相差2
因为“偶数-奇数=奇数”,只能确定另一个数是奇数,不能确定是质数还是合数。
(4)如下图,下面各说法错误的是( )。
A
A.甲和乙公有的质因数是1
B.甲和乙的最大公因数是8
C.甲和乙都是偶数
D.甲和乙的最小公倍数是96
甲和乙公有的质因数应该是2,1不是质数;
甲和乙的最大公因数能从图中看出来,是8;
甲和乙都有公因数2,因此甲和乙都是偶数;
甲是24,乙是32,最小公倍数是96。
甲的因数
乙的因数
甲和乙的公因数
1、2、
4、8
3、6、
12、24
16、32、
2
小林的爸爸是每4天休息一天,妈妈是每5天休息一天;两人同时休息的日子之间间隔的天数是4和5的公倍数;4和5互质,最小公倍数就是它们的乘积。
4×5=20(天)
6月1日+20天=6月21日
答:下一次同时在家休息是6月21日。
4.小林的爸爸每上班3天休息1天,妈妈每上班4天休息1天。6月1日他们同时在家休息,下一次同时在家休息是几月几日?
5.某工厂大约有100人,将他们按每组8人分组,多5人,按每组12人分组,也多5人。这个工厂有多少人?
(总人数-5)是8和12的公倍数。
8和12的公倍数有24、48、72、96、120……
其中最接近100的是96。
96+5=101(人)
答:这个工厂有101人。
6.一个三位数既是2的倍数,又是3的倍数,而且个位、十位上的数字相同,这个三位数最大是多少?
综合题意,从“这个三位数最大”考虑,百位上最大选9;再考虑“是2的倍数”,个位上可能是0、2、4、6或8;从900、922、944、966、988里选择3的倍数,符合条件的是900和966。
答:这个三位数最大是966。
6 整理和复习
1.数与代数
数学人教版六年级下册
第4课时 练习
练习巩固
1.填空。
零下为负,负数前面的“-”不可以省略。
(1)2008年8月3日,气象部门在新疆吐鲁番盆地的艾丁湖观测到的最高气温是49.7 ℃,可记作 ℃。1969年2月13日,气象部门在黑龙江漠河观测到的最低气温是零下52.3 ℃,可记作 ℃。
-52.3
49.7或+49.7
零上为正,正数前面的“+”可以省略不写。
(教材第73页练习十四)
较小数
可以用100-100×70%=30(元),也可用100×(1-70%)=30(元)。
(2)如果a÷b=c(a、b、c均为整数,且b≠0),那么a和b的最大公因数是_____,最小公倍数是_____。
a
b
a和b有倍数关系
较大数
(3)一种商品打七折销售,“七折”表示现价是原价的( )%。如果这种商品原价是100元,付款时要少付( )元。
70
30
2.下表是我国2017年、2019年、2021年全国城镇常住人口数量、全年粮食产量和全年消费品零售总额的相关数据。
年份 全国城镇常住人口数量/万人 全年粮食产量/万吨 全年消费品零售总额/亿元
2017 81347 61791 366262
2019 84843 66384 411649
2021 91425 68285 440823
年份 全国城镇常住人口数量/万人 全年粮食产量/万吨 全年消费品零售总额/亿元
2017 81347 61791 366262
2019 84843 66384 411649
2021 91425 68285 440823
(1)2017年,全国城镇常住人口约为_____亿人。(结果保留两位小数。)
8.13
年份 全国城镇常住人口数量/万人 全年粮食产量/万吨 全年消费品零售总额/亿元
2017 81347 61791 366262
2019 84843 66384 411649
2021 91425 68285 440823
(2)2019年,全年粮食产量约为_____亿吨。(结果保留两位小数。)
6.64
年份 全国城镇常住人口数量/万人 全年粮食产量/万吨 全年消费品零售总额/亿元
2017 81347 61791 366262
2019 84843 66384 411649
2021 91425 68285 440823
(3)2021年,全年消费品零售总额约为_____万亿元。(结果保留两位小数。)
44.08
年份 全国城镇常住人口数量/万人 全年粮食产量/万吨 全年消费品零售总额/亿元
2017 81347 61791 366262
2019 84843 66384 411649
2021 91425 68285 440823
(4)根据上表,你还能提出什么数学问题?
2021年全国城镇常住人口数量比2017年增长百分之几?
3.说出下面各数中“6”表示的含义。
63
0.56
603.7
6
7
“6”在十位上表示“6个十”
十位的计数单位是“十”
“6”在百分位上表示“6个0.01”
百分位的计数单位是“0.01”
“6”在百位上表示“6个百”
百位的计数单位是“百”
“6”在分子上表示“6个 ”
1
7
分数单位是“ ”
1
7
4.填空,使每横行的各数相等。
小数 分数 百分数
0.4
80%
4
5
3
4
25
40%
75%
0.75
0.8
= =
4
10
小数点向右移两位,加上“%”
分子÷分母
分子分母同时×25
约分
小数点向左移两位,去掉“%”
先改写成分母是10,100,1000,…的分数,再约分
用分子除以分母,除不尽的一般保留两位小数
小数点向右移两位,加上“%”
小数点向左移两位,去掉“%”
写成分数形式,并约分
先改写成小数,再改写成百分数
小数
分数
百分数
分数、小数与
百分数的互化
除不尽的一般保留三位小数
5.数字2、3、4、5能组成多少个没有重复数字的两位数?
十位是2:
23
24
25
十位是3:
32
34
35
十位是4:
42
43
45
十位是5:
52
53
54
(1)这些两位数中,哪些是奇数?哪些是偶数?
答:奇数有23、25、35、43、45、53;
偶数有24、32、34、42、52、54。
(2)这些两位数中,哪些是质数?哪些是合数?
答:质数有23、43、53;合数有24、25、32、34、35、42、45、52、54。
5.数字2、3、4、5能组成多少个没有重复数字的两位数?
十位是2:
23
24
25
十位是3:
32
34
35
十位是4:
42
43
45
十位是5:
52
53
54
(3)这些两位数中,哪些是2的倍数?哪些是3的倍数?哪些是5的倍数?
答:2的倍数有24、32、34、42、52、54;3的倍数有24、42、45、54;5的倍数有25、35、45。
(4)这些两位数中,2和3的公倍数是 ,3和5的公倍数是 。
24、42、54
45
都从合数里选择
从3的倍数里选择偶数
从3的倍数里选择5的倍数
6.判断下面的说法是否正确,并说一说你的理由。
(1)把0.56扩大到它的100倍是560。
(2)0是正数。
(3)假分数的倒数一定都是真分数。
(4)所有的偶数都是合数。
(5)a(a为整数,a>1)的所有因数都小于a。
小数点向右移2位,应该是56。
不正确
不正确
不正确
不正确
不正确
0既不是正数也不是负数。
分子分母相同的假分数的倒数还是假分数。
2是偶数但不是合数。
a的因数可以是它本身。
7.找规律,填数。
(1)0.9,0.99,0.999,0.9999,( ),…,这列数越来越大,越来越接近( )。
0.99999
1
1个9
2个9
3个9
4个9
5个9
0.9
1
+0.1
0.99
1
+0.01
0.999
1
+0.001
+0.0001
0.9999
1
……
1
64
(2) , , , , ,( ),…,这列数越来越小,越来越接近( )。
1
32
1
16
1
8
1
4
1
2
1
32
1
16
1
8
1
4
1
2
1
64
1
64
×
1
2
×
1
2
×
1
2
×
1
2
×
1
2
1
2
1
4
1
8
1
16
1
32
0
8.比较 、 、 、 的大小,你能发现什么?
1
2
5
6
2
3
3
4
< < <
1
2
5
6
2
3
3
4
1
2
5
6
2
3
3
4
8.比较 、 、 、 的大小,你能发现什么?
1
2
5
6
2
3
3
4
< < <
1
2
5
6
2
3
3
4
猜
想:
17
18
19
20
<
验证:
17
18
170
180
=
19
20
171
180
=
根据你发现的规律猜一下 与 哪个更大,并设法验证。
17
18
19
20
170
180
<
171
180
17
18
19
20
<
所以
我发现这些分数的分子都比分母小1,当分子、分母越大时,这个分数就越大。
因为
9.*一箱苹果,如果每8个装一盒,还剩余6个;如果每10个装一盒,也剩余6个。这箱苹果至少有多少个?
由题意可知,(苹果数-6)是8和10的公倍数。
8和10的最小公倍数是40。
40+6=46(个)
答:这箱苹果至少有46个。
求至少有多少个,就是求8和10的最小公倍数加6是多少。
拓展提升
1.把一张长32厘米、宽24厘米的长方形剪成同样大小,且面积尽可能大的正方形(没有剩余)。一共可以剪多少个这样的正方形?
剪成的形状是正方形,说明正方形的边长是长方形长和宽的公因数;要正方形尽可能大,就是求长方形长和宽的最大公因数。
因为32和24的最大公因数是8,所以正方形的边长是8厘米。
(32÷8)×(24÷8)=12(个)
答:一共可以剪12个这样的正方形。
2.表演队在操场上列队,人数在90~110范围内,且他们排成3列无余,排成5列差2人,排成7列差4人,共多少人?
由题意可知,(总人数-3)是3、5、7的公倍数。
3、5、7的公倍数有105、210……符合题意的是105。
105+3=108(人)
答:共有108人。
余3人
余3人
余3人
求解同余同差问题,就是先求几个数的公倍数,再加上同余或减去同差。
Thank you!
