21.3 用待定系数法确定一次函数表达式 课件(共19张PPT) 冀教版八年级下册
文档属性
| 名称 | 21.3 用待定系数法确定一次函数表达式 课件(共19张PPT) 冀教版八年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-06 00:00:00 | ||
图片预览






文档简介
(共19张PPT)
21.3 用待定系数法确定一次函数表达式
第二十一章 一次函数
学习目标
1.学会用待定系数法确定一次函数表达式;
2.运用待定系数法解决相关问题.
学习重难点
学会用待定系数法确定一次函数表达式.
运用待定系数法解决相关问题.
难点
重点
回顾复习
函数的表示
数值表法
表达式法
列表
描点
用描点法
画函数图像
可以具体地看出自变量的取值及函数的对应值
连线
图像法
形象直观地显示出函数的变化规律
准确反映了函数与自变量之间的数量关系,便于抽象应用
创设情境
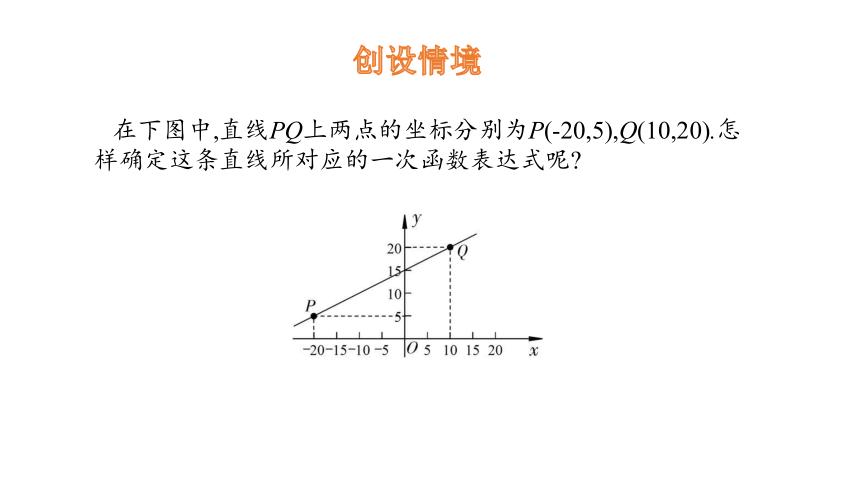
在下图中,直线PQ上两点的坐标分别为P(-20,5),Q(10,20).怎样确定这条直线所对应的一次函数表达式呢
设这个一次函数表达式为.
因为P,Q为直线上的两点,所以这两个点的坐标都满足表达式,即
解这个关于k和b的二元一次方程组,得,
所以,这个一次函数的表达式为
知识点1 用待定系数法确定一次函数表达式
新知引入
定义:像这样,先设出函数表达式,再根据已知条件确定表达式中未知的系数,从而求出函数表达式的方法称为待定系数法.
归纳
做一做
1.已知点A(-20,5)为正比例函数y=kx图像的一点,求这个正比例函数表达式.
解:将点A的坐标代入正比例函数表达式可得 ,解得
所以正比例函数表达式为
做一做
2.已知一个一次函数的图像经过点M(0,1)和点N(1,0),求这个一次函数表达式.
解:设一次函数表达式为y=kx+b.
将点M,N的坐标代入上式可得
解得 ,
所以,这个一次函数的表达式为1
例题示范
一辆汽车匀速行驶,当行驶了20 km时,油箱剩余58.4 L油;当行驶了50 km时,油箱剩余56 L油.如果油箱中剩余油量 y (L)与汽车行驶的路程 x (km)之间是一次函数关系,请求出这个一次函数的表达式,并写出自变量 x 的取值范围以及常数项的意义.
解:设所求一次函数的表达式为y=kx+b.
根据题意,把已知的两组对应值(20,58.4)和(50,56)代入,
得 ,解得
这个一次函数表达式为
例题示范
一辆汽车匀速行驶,当行驶了20 km时,油箱剩余58.4 L油;当行驶了50 km时,油箱剩余56 L油.如果油箱中剩余油量 y (L)与汽车行驶的路程 x (km)之间是一次函数关系,请求出这个一次函数的表达式,并写出自变量 x 的取值范围以及常数项的意义.
因为剩余油量y≥0,所以;
解得:.
因为路程,所以
因为当x=0时,y=60,所以这辆汽车行驶前油箱存油60L.
归纳
求一次函数表达式的步骤:
(1)设:设一次函数表达式y=kx+b(k≠0);
(2)列:根据条件,列出关于k和b的二元一次方程组;
(3)解:解二元一次方程组求出k,b的值,从而得到一次函数的表达式.
1. 已知一次函数y=x+b过点(-1,-2),那么这个函数解析式为( )
A.y=x-1
B.y=x+1
C.y=x-2
D.y=x+2
A
随堂练习
2.一次函数的图像经过点P (0,2), Q(1,3)两点,则k,b的值分别是( )
A. -1,-2
B. 1,2
C. -2,-1
D. 2,1
B
3. 如图,在平面直角坐标系中,直线l经过点A(0,3),且与直线y=2x平行,那么直线l的函数表达式是( )
A.
B.
C.
D.
A
1. 如图,在平面直角坐标系中,A(2,0),B(0,1),AC=AB且AC⊥AB,AC⊥AB,则BC所在的直线的表达式是( )
A.
B.
C.
D.
拓展提升
C
2. 直线AB与x轴交于点A(2,0),与y轴交于点B(0,-4).
(1)求直线AB的函数表达式;
(2)若x轴负半轴上存在点C,使△ABC的面积等于10,求点C的坐标.
解:(1)设直线AB的表达式为,
将A(2,0),B(0,-4)代入,
得 解得
∴直线AB的表达式为
2. 直线AB与x轴交于点A(2,0),与y轴交于点B(0,-4).
(1)求直线AB的函数表达式;
(2)若x轴负半轴上存在点C,使△ABC的面积等于10,求点C的坐标.
(2)∵B(0,-4),∴OB=4.
∵△ABC的面积等于10,
∴,∴AC=5
∵点C在x轴负半轴上,且A(2,0),
∴点C的坐标为(-3,0).
3. 如图,一束光线从点A(3,2)出发,经x轴上的点C反射后经过点B(0,1),则点C的坐标是_____.
(1,0)
归纳小结
用待定系数法确定一次函数表达式
求一次函数表达式的步骤:
(1)设:设一次函数表达式y=kx+b(k≠0);
(2)列:根据条件,列出关于k和b的二元一次方程组;
(3)解:解二元一次方程组求出k,b的值,从而得到一次函数的表达式.
21.3 用待定系数法确定一次函数表达式
第二十一章 一次函数
学习目标
1.学会用待定系数法确定一次函数表达式;
2.运用待定系数法解决相关问题.
学习重难点
学会用待定系数法确定一次函数表达式.
运用待定系数法解决相关问题.
难点
重点
回顾复习
函数的表示
数值表法
表达式法
列表
描点
用描点法
画函数图像
可以具体地看出自变量的取值及函数的对应值
连线
图像法
形象直观地显示出函数的变化规律
准确反映了函数与自变量之间的数量关系,便于抽象应用
创设情境
在下图中,直线PQ上两点的坐标分别为P(-20,5),Q(10,20).怎样确定这条直线所对应的一次函数表达式呢
设这个一次函数表达式为.
因为P,Q为直线上的两点,所以这两个点的坐标都满足表达式,即
解这个关于k和b的二元一次方程组,得,
所以,这个一次函数的表达式为
知识点1 用待定系数法确定一次函数表达式
新知引入
定义:像这样,先设出函数表达式,再根据已知条件确定表达式中未知的系数,从而求出函数表达式的方法称为待定系数法.
归纳
做一做
1.已知点A(-20,5)为正比例函数y=kx图像的一点,求这个正比例函数表达式.
解:将点A的坐标代入正比例函数表达式可得 ,解得
所以正比例函数表达式为
做一做
2.已知一个一次函数的图像经过点M(0,1)和点N(1,0),求这个一次函数表达式.
解:设一次函数表达式为y=kx+b.
将点M,N的坐标代入上式可得
解得 ,
所以,这个一次函数的表达式为1
例题示范
一辆汽车匀速行驶,当行驶了20 km时,油箱剩余58.4 L油;当行驶了50 km时,油箱剩余56 L油.如果油箱中剩余油量 y (L)与汽车行驶的路程 x (km)之间是一次函数关系,请求出这个一次函数的表达式,并写出自变量 x 的取值范围以及常数项的意义.
解:设所求一次函数的表达式为y=kx+b.
根据题意,把已知的两组对应值(20,58.4)和(50,56)代入,
得 ,解得
这个一次函数表达式为
例题示范
一辆汽车匀速行驶,当行驶了20 km时,油箱剩余58.4 L油;当行驶了50 km时,油箱剩余56 L油.如果油箱中剩余油量 y (L)与汽车行驶的路程 x (km)之间是一次函数关系,请求出这个一次函数的表达式,并写出自变量 x 的取值范围以及常数项的意义.
因为剩余油量y≥0,所以;
解得:.
因为路程,所以
因为当x=0时,y=60,所以这辆汽车行驶前油箱存油60L.
归纳
求一次函数表达式的步骤:
(1)设:设一次函数表达式y=kx+b(k≠0);
(2)列:根据条件,列出关于k和b的二元一次方程组;
(3)解:解二元一次方程组求出k,b的值,从而得到一次函数的表达式.
1. 已知一次函数y=x+b过点(-1,-2),那么这个函数解析式为( )
A.y=x-1
B.y=x+1
C.y=x-2
D.y=x+2
A
随堂练习
2.一次函数的图像经过点P (0,2), Q(1,3)两点,则k,b的值分别是( )
A. -1,-2
B. 1,2
C. -2,-1
D. 2,1
B
3. 如图,在平面直角坐标系中,直线l经过点A(0,3),且与直线y=2x平行,那么直线l的函数表达式是( )
A.
B.
C.
D.
A
1. 如图,在平面直角坐标系中,A(2,0),B(0,1),AC=AB且AC⊥AB,AC⊥AB,则BC所在的直线的表达式是( )
A.
B.
C.
D.
拓展提升
C
2. 直线AB与x轴交于点A(2,0),与y轴交于点B(0,-4).
(1)求直线AB的函数表达式;
(2)若x轴负半轴上存在点C,使△ABC的面积等于10,求点C的坐标.
解:(1)设直线AB的表达式为,
将A(2,0),B(0,-4)代入,
得 解得
∴直线AB的表达式为
2. 直线AB与x轴交于点A(2,0),与y轴交于点B(0,-4).
(1)求直线AB的函数表达式;
(2)若x轴负半轴上存在点C,使△ABC的面积等于10,求点C的坐标.
(2)∵B(0,-4),∴OB=4.
∵△ABC的面积等于10,
∴,∴AC=5
∵点C在x轴负半轴上,且A(2,0),
∴点C的坐标为(-3,0).
3. 如图,一束光线从点A(3,2)出发,经x轴上的点C反射后经过点B(0,1),则点C的坐标是_____.
(1,0)
归纳小结
用待定系数法确定一次函数表达式
求一次函数表达式的步骤:
(1)设:设一次函数表达式y=kx+b(k≠0);
(2)列:根据条件,列出关于k和b的二元一次方程组;
(3)解:解二元一次方程组求出k,b的值,从而得到一次函数的表达式.
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
