21.4 一次函数的应用 第1课时 课件(共17张PPT) 冀教版数学八年级下册
文档属性
| 名称 | 21.4 一次函数的应用 第1课时 课件(共17张PPT) 冀教版数学八年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-06 19:04:07 | ||
图片预览





文档简介
(共17张PPT)
21.4 一次函数的应用
第1课时
第二十一章 一次函数
学习目标
1.能根据题目条件确定函数关系式,能利用一次函数的性质及其图像解决简单的实际问题;
2.经历把实际问题抽象成数学模型的过程,培养学生的建模意识.
学习重难点
利用一次函数的性质及其图像解决简单的实际问题.
把实际问题抽象成数学模型,对数学建模的过程、思想、方法的领会.
难点
重点
回顾复习
用待定系数法确定一次函数表达式
求一次函数表达式的步骤:
(1)设:设一次函数表达式y=kx+b(k≠0);
(2)列:根据条件,列出关于k和b的二元一次方程组;
(3)解:解二元一次方程组求出k,b的值,从而得到一次函数的表达式.
创设情境
利用一次函数这一数学模型,可以解决许多与其相关的实际问题和数学自身的问题.
某公司与销售人员签订了这样的工资合同:工资由两部分组成,一部分是基本工资,每人每月3000元;另一部分是按月销售量确定的奖励工资,每销售1件产品,奖励工资10元.
1.设某销售员月销售产品x件,他应得的工资记为y元.求y与x之间的函数关系式.
知识点1 一次函数的应用——文字表述型
新知引入
解:工资=基本工资+奖励工资
所以y与x之间的函数关系式为y=10x+3000.
试着做做
2.用求出的函数关系式y=10x+3000,尝试解决下列问题:
(1)该销售员某月的工资为4100元,他这个月销售了多少件产品
(2)要想使月工资超过4500元,该月的销售量应当超过多少件
解:
(1)当销售员的月工资为4100元时,有4100=10x+3000,解得x=110.
(2)要想使月工资超过4500元,只要使10x+3000>4500即可.解得x>150.
试着做做
一起探究
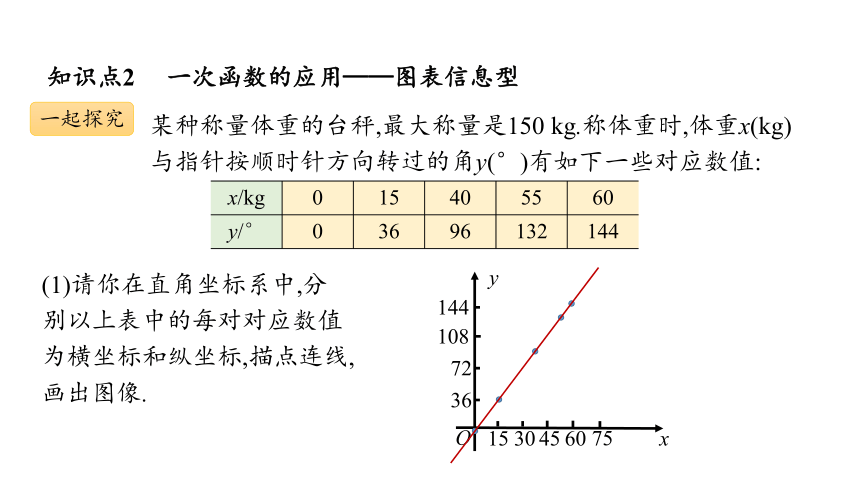
某种称量体重的台秤,最大称量是150 kg.称体重时,体重x(kg)与指针按顺时针方向转过的角y(°)有如下一些对应数值:
知识点2 一次函数的应用——图表信息型
x/kg 0 15 40 55 60
y/° 0 36 96 132 144
y
15
30
45
60
x
36
72
108
144
O
75
(1)请你在直角坐标系中,分别以上表中的每对对应数值为横坐标和纵坐标,描点连线,画出图像.
一起探究
某种称量体重的台秤,最大称量是150 kg.称体重时,体重x(kg)与指针按顺时针方向转过的角y(°)有如下一些对应数值:
x/kg 0 15 40 55 60
y/° 0 36 96 132 144
(2)求y与x之间的函数关系式,并指出自变量x的取值范围.
解:由表格给出的数据结合图像可以看出,体重为0 kg时,台秤指针指向0°,每增加5 kg,台秤指针按顺时针方向旋转12°,所以y是x的正比例函数. 根据条件可得,
()
一起探究
某种称量体重的台秤,最大称量是150 kg.称体重时,体重x(kg)与指针按顺时针方向转过的角y(°)有如下一些对应数值:
x/kg 0 15 40 55 60
y/° 0 36 96 132 144
(3)当体重为多少千克时,台秤的指针恰好转到180°的位置 当体重为50 kg时,台秤的指针转过的角度是多少
解:当y=180时,. 解得x=75.
当x=50时,. 解得y=120.
即当体重为75 kg时,台秤的指针恰好转到180°的位置;当体重为50 kg时,台秤的指针转过的角度是120°.
归纳
用一次函数解决实际问题
1.读题后分析题意,理顺关系,寻求解题途径.
2.要注意结合实际,确定自变量的取值范围,有
时对同一个问题,不同的自变量取值范围会有不
同的函数关系.
随堂练习
1.如图,快递小哥的日收入y(元)与每日的派送量x(件)成一次函数关系.
(1)写出x和y的函数关系式.
(2)某天快递小哥的收入为180元,则他派送了多少件?
解:(1)设快递小哥的日收入y(元)与每日的派送量x(件)之间的函数关系式为y=kx+b(k≠0),把(0,70),(30,100)代入,得b=70,30k+b=100,解得k=1,所以该函数的关系式为y=x+70.
(2)将y=180代入,得x=110,即他派送了110件.
2.某瓷器厂生产的瓷碗按如图所示方式放置,3个瓷碗的高度是9cm,每增加1个瓷碗,瓷碗堆的高度将增加1.5cm.
(1)写出瓷碗堆高度y(cm)与瓷碗个数x之间的函数关系式.
(2)当瓷碗个数为10个时,瓷碗堆的高度是多少?
解:(1)设瓷碗堆高度y(cm)与瓷碗个数x之间的函数关系式为y=1.5x+b(k≠0),把x=3,y=9代入,得9=1.5×3+b,解得b=4.5,所以该函数的关系式为y=1.5x+4.5 .
(2)将x=10代入,得y=19.5,即瓷碗堆的高度为19.5cm.
3.小王从家骑车到公园,她到公园的距离y(km)与骑行时间x(min)的关系如图所示.
(1)写出小王到公园的距离y(km)与骑行时间x(min)之间的函数关系式.
(2)小王从家到公园用了多长时间?
(3)出发8min后,小王离公园还有多远?
解:(1)设小王到公园的距离y(km)与骑行时间x(min)之间的函数关系式为y=kx+b(k≠0),将(0,15),(10,10)代入,得b=15,10k+b=10,解得k=,所以该函数的关系式为 .
3.小王从家骑车到公园,她到公园的距离y(km)与骑行时间x(min)的关系如图所示.
(1)写出小王到公园的距离y(km)与骑行时间x(min)之间的函数关系式.
(2)小王从家到公园用了多长时间?
(3)出发8min后,小王离公园还有多远?
(2)将y=0代入,得x=30,即小王从家到公园用了30min.
(3)将x=8代入,得y=×8+15=11,即小王离公园还有11km.
拓展提升
1.秤是我国传统的计重工具,其秤砣到秤纽的水平距离y(cm)与秤钩所挂物重x(kg)之间满足一次函数关系. 若不挂重物时秤砣到秤纽的水平距离为2.5cm,挂1kg重物时秤砣到秤纽的水平距离为8cm,则当秤砣到秤纽的水平距离为30cm时,秤钩所挂物重为多少kg?
解:设秤砣到秤纽的水平距离y(cm)与秤钩所挂物重x(kg)之间的函数关系式为y=kx+2.5,将x=1,y=8代入,得8=k+2.5,解得k=,所以该函数的关系式为 .
当秤砣到秤纽的水平距离为30cm时,有30=5.5x+2.5,解得x=5,即秤钩所挂物重为5kg.
2.一个装有进水管和出水管的容器,从某时刻起开始的4 min 内只进水不出水,在随后的8 min 内既进水又出水,每分钟的进水量和出水量是两个常数.容器内的水量 y(单位: L )与时间 x(单位: min)之间的关系如图,则第8min时容器内的水量为多少?
解:当时,设y关于x的函数关系式为y=kx+b,
∵点(4,20),(12,30)在该函数的图像上,∴ 解得
即当时,y关于x的函数关系式为.
当x=8时,y=×8+15=25. 即第8min时容器内的水量为25L.
归纳小结
实际问题转化为数学模型,利用一次函数的性质及其图像解决简单的实际问题.
用一次函数
解决实际问题
21.4 一次函数的应用
第1课时
第二十一章 一次函数
学习目标
1.能根据题目条件确定函数关系式,能利用一次函数的性质及其图像解决简单的实际问题;
2.经历把实际问题抽象成数学模型的过程,培养学生的建模意识.
学习重难点
利用一次函数的性质及其图像解决简单的实际问题.
把实际问题抽象成数学模型,对数学建模的过程、思想、方法的领会.
难点
重点
回顾复习
用待定系数法确定一次函数表达式
求一次函数表达式的步骤:
(1)设:设一次函数表达式y=kx+b(k≠0);
(2)列:根据条件,列出关于k和b的二元一次方程组;
(3)解:解二元一次方程组求出k,b的值,从而得到一次函数的表达式.
创设情境
利用一次函数这一数学模型,可以解决许多与其相关的实际问题和数学自身的问题.
某公司与销售人员签订了这样的工资合同:工资由两部分组成,一部分是基本工资,每人每月3000元;另一部分是按月销售量确定的奖励工资,每销售1件产品,奖励工资10元.
1.设某销售员月销售产品x件,他应得的工资记为y元.求y与x之间的函数关系式.
知识点1 一次函数的应用——文字表述型
新知引入
解:工资=基本工资+奖励工资
所以y与x之间的函数关系式为y=10x+3000.
试着做做
2.用求出的函数关系式y=10x+3000,尝试解决下列问题:
(1)该销售员某月的工资为4100元,他这个月销售了多少件产品
(2)要想使月工资超过4500元,该月的销售量应当超过多少件
解:
(1)当销售员的月工资为4100元时,有4100=10x+3000,解得x=110.
(2)要想使月工资超过4500元,只要使10x+3000>4500即可.解得x>150.
试着做做
一起探究
某种称量体重的台秤,最大称量是150 kg.称体重时,体重x(kg)与指针按顺时针方向转过的角y(°)有如下一些对应数值:
知识点2 一次函数的应用——图表信息型
x/kg 0 15 40 55 60
y/° 0 36 96 132 144
y
15
30
45
60
x
36
72
108
144
O
75
(1)请你在直角坐标系中,分别以上表中的每对对应数值为横坐标和纵坐标,描点连线,画出图像.
一起探究
某种称量体重的台秤,最大称量是150 kg.称体重时,体重x(kg)与指针按顺时针方向转过的角y(°)有如下一些对应数值:
x/kg 0 15 40 55 60
y/° 0 36 96 132 144
(2)求y与x之间的函数关系式,并指出自变量x的取值范围.
解:由表格给出的数据结合图像可以看出,体重为0 kg时,台秤指针指向0°,每增加5 kg,台秤指针按顺时针方向旋转12°,所以y是x的正比例函数. 根据条件可得,
()
一起探究
某种称量体重的台秤,最大称量是150 kg.称体重时,体重x(kg)与指针按顺时针方向转过的角y(°)有如下一些对应数值:
x/kg 0 15 40 55 60
y/° 0 36 96 132 144
(3)当体重为多少千克时,台秤的指针恰好转到180°的位置 当体重为50 kg时,台秤的指针转过的角度是多少
解:当y=180时,. 解得x=75.
当x=50时,. 解得y=120.
即当体重为75 kg时,台秤的指针恰好转到180°的位置;当体重为50 kg时,台秤的指针转过的角度是120°.
归纳
用一次函数解决实际问题
1.读题后分析题意,理顺关系,寻求解题途径.
2.要注意结合实际,确定自变量的取值范围,有
时对同一个问题,不同的自变量取值范围会有不
同的函数关系.
随堂练习
1.如图,快递小哥的日收入y(元)与每日的派送量x(件)成一次函数关系.
(1)写出x和y的函数关系式.
(2)某天快递小哥的收入为180元,则他派送了多少件?
解:(1)设快递小哥的日收入y(元)与每日的派送量x(件)之间的函数关系式为y=kx+b(k≠0),把(0,70),(30,100)代入,得b=70,30k+b=100,解得k=1,所以该函数的关系式为y=x+70.
(2)将y=180代入,得x=110,即他派送了110件.
2.某瓷器厂生产的瓷碗按如图所示方式放置,3个瓷碗的高度是9cm,每增加1个瓷碗,瓷碗堆的高度将增加1.5cm.
(1)写出瓷碗堆高度y(cm)与瓷碗个数x之间的函数关系式.
(2)当瓷碗个数为10个时,瓷碗堆的高度是多少?
解:(1)设瓷碗堆高度y(cm)与瓷碗个数x之间的函数关系式为y=1.5x+b(k≠0),把x=3,y=9代入,得9=1.5×3+b,解得b=4.5,所以该函数的关系式为y=1.5x+4.5 .
(2)将x=10代入,得y=19.5,即瓷碗堆的高度为19.5cm.
3.小王从家骑车到公园,她到公园的距离y(km)与骑行时间x(min)的关系如图所示.
(1)写出小王到公园的距离y(km)与骑行时间x(min)之间的函数关系式.
(2)小王从家到公园用了多长时间?
(3)出发8min后,小王离公园还有多远?
解:(1)设小王到公园的距离y(km)与骑行时间x(min)之间的函数关系式为y=kx+b(k≠0),将(0,15),(10,10)代入,得b=15,10k+b=10,解得k=,所以该函数的关系式为 .
3.小王从家骑车到公园,她到公园的距离y(km)与骑行时间x(min)的关系如图所示.
(1)写出小王到公园的距离y(km)与骑行时间x(min)之间的函数关系式.
(2)小王从家到公园用了多长时间?
(3)出发8min后,小王离公园还有多远?
(2)将y=0代入,得x=30,即小王从家到公园用了30min.
(3)将x=8代入,得y=×8+15=11,即小王离公园还有11km.
拓展提升
1.秤是我国传统的计重工具,其秤砣到秤纽的水平距离y(cm)与秤钩所挂物重x(kg)之间满足一次函数关系. 若不挂重物时秤砣到秤纽的水平距离为2.5cm,挂1kg重物时秤砣到秤纽的水平距离为8cm,则当秤砣到秤纽的水平距离为30cm时,秤钩所挂物重为多少kg?
解:设秤砣到秤纽的水平距离y(cm)与秤钩所挂物重x(kg)之间的函数关系式为y=kx+2.5,将x=1,y=8代入,得8=k+2.5,解得k=,所以该函数的关系式为 .
当秤砣到秤纽的水平距离为30cm时,有30=5.5x+2.5,解得x=5,即秤钩所挂物重为5kg.
2.一个装有进水管和出水管的容器,从某时刻起开始的4 min 内只进水不出水,在随后的8 min 内既进水又出水,每分钟的进水量和出水量是两个常数.容器内的水量 y(单位: L )与时间 x(单位: min)之间的关系如图,则第8min时容器内的水量为多少?
解:当时,设y关于x的函数关系式为y=kx+b,
∵点(4,20),(12,30)在该函数的图像上,∴ 解得
即当时,y关于x的函数关系式为.
当x=8时,y=×8+15=25. 即第8min时容器内的水量为25L.
归纳小结
实际问题转化为数学模型,利用一次函数的性质及其图像解决简单的实际问题.
用一次函数
解决实际问题
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
